Часть 4 основы квантовой электроники

Литература:

А.Н. Пихтин, «Физические основы

квантовой электроники и оптоэлектроники»

§ 1. Электронные состояния атомов

Квантовое состояние электрона в атоме определяется набором четырех квантовых чисел n, l, m_l, m_s.

n = 1, 2, 3, …

l = 0, 1, 2, … n – 1

m_l = -l...0…l

m_s = -1/2, 1/2

1) n характеризует «размер» электронной «орбиты» (точнее «орбитали» - области преимущественной локализации электронного облака) и величину основной части энергии электрона.

n = 1, 2, 3, … n – главное квантовое число.

2) l характеризует «вытянутость», несферичность электронной орбитали и определяет модуль вектора момента количества движения (мкд) электрона по орбите вокруг ядра .

l = 0, 1, 2, … n – 1

l – орбитальное (азимутальное) квантовое число.

3) m_l характеризует наклон, ориентацию плоскости электронной орбиты относительно преимущественного направления и определяет величину проекции вектора орбитального мкд на преимущественное направление.

m_l = -l...0…l (всего 2l + 1 значений) ( = h/2π )

m_l – магнитное квантовое число.

4) s характеризует (в теории Бора) вращение электрона вокруг своей оси и определяет модуль вектора спинового мкд вращения электрона вокруг своей оси.

m_s – определяет проекцию на z

m_s – магнитное спиновое квантовое число

(Часто оба числа s и m_s называют спиновыми квантовыми числами)

s = 1/2 m_s = ±1/2

В квантовой механике нельзя утверждать о вращении электрона вокруг своей оси, это просто наглядное упрощение.

Иногда пользуются пятым квантовым числом – j (внутреннее квантовое число), которое определяет в единицах полный момент количества движения (МКД) как сумму орбитального и спинового моментов.

;

Но j – в отличие от 4^х остальных квантовых чисел не независимо, оно определяется суммированием и .

Число j меняется от |l – s| до |l + s| через 1.

Используют также квантовое число

m_j , определяющее проекцию на (т. е. на z , т.к. направления и z совпадают)

m_j меняется от –j до j, т.е. имеет 2j + 1 разных значений.

Для сложных атомов обычно пользуются системой квантовых чисел n, l, s, j, m_j.

Для атома водорода – n, l, m_l, s, m_s.

Все состояния с заданными n и l образуют электронную оболочку (например, 1s – оболочку, 2р – оболочку и т.д.). Число электронов в оболочке записывается символом справа вверху, например 2р⁴ обозначает 4 электрона в состоянии 2р.

По числам m_l и m_s энергетические уровни вырождены, т.е. энергия не зависит от m_l и m_s. Число разных квантовых состояний с одной и той же энергией Е - кратность вырождения или статистический вес.

Максимальное число электронов в s-оболочке -2, р – 6, d – 10, f – 14.

Все квантовые состояния с данным п и любыми другими квантовыми числами называются электронным слоем. В слое могут быть 2п² электронов. Обозначают слои K, L, M, N, O, что соответствует п = 1, 2, 3, 4, 5, …

Электронная конфигурация атома – это перечень полностью или частично заполненных электронных оболочек. Для азота, например, (Z=7) 1s²2s²2p³ – (иногда записывают (1s)² (2s)² (2p)³). Для упрощения нижние заполненные, кроме того, когда на оболочке один электрон, цифру 1 не пишут. Например, электронная конфигурация для атома Na обозначается 3s¹ или просто 3s, а 1s²2s²2p⁶ не записывают.

Чем больше п, тем ближе по энергиям соседние электронные оболочки.

Е

Рис.1

При больших п возможны случаи, когда состояния с разными n и l имеют примерно одинаковые энергии. Какие же из них будут заполнены электронами? Ведь электроны стремятся занять состояния с наименьшей энергией. Или, например, у азота для оболочки 2р³ – 3 электрона, а мест – 6. Как они заполняются?

Для установления порядка заполнения квантовых состояний электронами существуют полуэмпирические правила Хунда:

внутри оболочки электроны распределяются таким образом, чтобы:

1) сумма чисел m_s по всем электронам данной оболочки была максимальной (это главное правило);

2) сумма чисел m_l по всем электронам данной оболочки тоже была максимальной (выполняется после 1)).

Поэтому сначала заполняется состояние m_s = 1/2, m_l = l, затем m_s = 1/2, m_l = l – 1 и т.д. Последним заполняется m_s = -1/2, m_l = -l.

У азота, следовательно, заполнены в оболочке 2р квантовые состояния m_l = 1, m_s = 1/2; m_l = 0, m_s = 1/2; m_l = -1, m_s = 1/2, а состояния с m_s = -1/2 (где m_l = 1, 0, -1) не заполнены.

Бывают случаи, когда внешняя (например, 4s) и внутренняя (3d) электронные оболочки имеют примерно одинаковые энергии. Тогда внутренняя оболочка может оказаться не полностью заполненной, т.к. часть электронов уйдет на внешнюю оболочку (так называемая переходная группа элементов). Например, у хрома (z = 24) электронная конфигурация невозбужденного атома - 1s²2s²2p⁶3s²3p⁶3d⁵4s¹.

В квантовой электронике играют существенную роль элементы группы железа с незастроенной 3d-оболочкой и редкоземельные металлы, или лантаноиды, с незастроенной 4f-оболочкой.

Квантовые состояния атома описываются орбитальным квантовым числом L, спиновым квантовым числом S, внутренним квантовым числом и магнитным квантовым числом

Существуют различные правила суммирования орбитальных и спиновых моментов электронов в атоме. Чаще всего встречается нормальная или LS-связь (или Расселсаундерсовская связь – по имени Рассела и Саундерса). Обычно она встречается для атомов или ионов с небольшим числом валентных электронов. У них взаимодействие спиновых моментов электронов между собой сильнее, чем взаимодействие спиновых моментов с орбитальными.

При нормальной связи выполняются следующие правила сложения моментов:

1. Орбитальные моменты всех электронов ориентируются друг относительно друга так, чтобы суммарный орбитальный момент атома имел целочисленное значение (в единицах )

L меняется от min до max значения , включая 0.

2. Спиновые моменты электронов ориентируются параллельно или антипараллельно друг другу, при этом спиновый момент атома должен быть целым (включая 0) при четном числе электронов или полуцелым при нечетном числе электронов (всё – в единицах )

S меняется от min до max значения

3. Орбитальный и спиновый моменты атома ориентируются друг относительно друга так, чтобы полный мкд атома был бы целым – при четном числе электронов либо полуцелым – при нечетном числе электронов.

+

Энергетическое состояние атома с заданными квантовыми числами L и S называется спектральным термом.

За счет релятивистских эффектов терм с заданными L и S расщепляется на ряд энергетических подуровней с различными значениями . Это называется тонкой структурой уровня или мультиплетным расщеплением уровня.

При L > S терм расщепляется на 2S + 1 подуровней.

При S > L терм расщепляется на 2L + 1 подуровней.

При этом не снимается вырождение по магнитному квантовому числу атома , которое определяет проекцию на (или другое выделенное направление) и имеет значений (от до включая ноль), т.е. остается кратность вырождения, равная .

Для обозначения атомных уровней энергии в приближении LS-связи принята следующая символика терма:

^2S+1 L_J

В зависимости от значения L его обозначают буквой:

S при L = 0 F при L = 3

P при L = 1 G при L = 4

D при L = 2 H при L = 5

2S + 1 называется мультиплетностью терма

Примеры термов:

¹S₀ L = 0, S = 0, = 0 (наинизший энергетический уровень)

²P_3/2 L = 1, S = 1/2, = 3/2

Иногда нужно задать значение , тогда его пишут справа вверху, например ( L = 2, S = 1, = 2, = -1).

Для полностью заполненных электронами оболочек L = S = = 0, поэтому для нахождения L и S всего атома следует учитывать только не полностью заполненные оболочки. Для полностью заполненных оболочек, таких как s², p⁶, d¹⁰ всегда имеется только один терм ¹S₀.

Рассмотрим энергетические состояния атомов гелия He и неона Ne.

He z = 2. Основное (невозбужденное) состояние имеет электронную конфигурацию 1s², которой соответствует один терм ¹S₀.

Наинизшее возбужденное состояние соответствует переходу одного электрона в состояние 2s, когда электронная конфигурация станет 1s¹2s¹.

Назовем «атомный остаток» - все электроны, кроме возбужденного.

Здесь атомный остаток – 1 электрон в состоянии 1s, для него квантовые числа S = ½, L = 0. У возбужденного электрона в состоянии 2s l = 0, s = ½ .

Значит, в целом для атома с конфигурацией 1s¹2s¹ возможны лишь два значения S – 0 и 1 и единственное значение L – 0, т.е.

L = 0, S = 0, = 0 – терм ¹S₀ записывается .

L = 0, S = 1, = 1 – терм ³S₁ записывается 2s ³S₁.

Значит, переходу одного электрона из состояния 1s в состояние 2s, т. е. возбужденному состоянию атома, соответствует два значения энергии атома, два терма: 2s¹S₀ и 2s³S₁.

У терма ³S₁ спиновое квантовое число больше, следовательно по правилу Хунда этот терм имеет меньшее значение энергии и раньше заполняется.

Ne z = 10. Основное состояние 1s²2s²2p⁶ – терм ¹S₀. Электронная конфигурация наинизшего возбужденного состояния 1s²2s²2p⁵3s¹.

У атомного остатка S = ½, L = 1, у возбужденного электрона s = ½, l = 0.

Поэтому в целом для атома в возбужденном состоянии возможны термы:

L = 1, S = 1, = 2 – терм 3s ³P₂

= 1 – терм 3s ³P₁

= 0 – терм 3s ³P₀

L = 1, S = 0, = 1 – терм 3s ¹P₁

Итак – 4 терма и 4 уровня энергии.

Так же, по 4 уровня для конфигураций 2p⁵4s¹, 2p⁵5s¹, 2p⁵6s¹. При переходе электрона в возбужденное р-состояние, т.е. для электронных конфигураций 2p⁵пр¹ (п = 3, 4, 5…) – по 10 разрешенных уровней энергии.

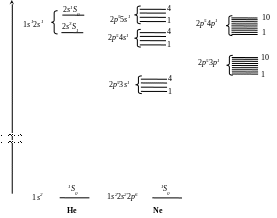
Е, эВ

20

16

2

0

Рис.2

Аналогично строятся схемы и для ионов. Схема для атома с атомным номером z, у которого удалены N электронов, близка к схеме атома с ат. номером z – N.

Кстати, у He синглетный терм 2s¹S₀ и триплетный терм 2s³S₁ метастабильны, т.к. переход вниз запрещен правилами отбора (должно быть ∆l = ±1), так что электрон может находиться на этих уровнях долго (по атомным масштабам) – порядка миллисекунды.

Ввиду правила ∆S = 0 интеркомбинационные переходы между синглетными и триплетными термами маловероятны.

Кроме LS - связи существуют и другие виды связи.

jj-связь – когда сильно взаимодействуют друг с другом орбитальный и спиновый моменты одного электрона. Тогда нужно сначала складывать , а уже затем суммировать по всем электронам . Символика обозначений здесь иная (не приводится). Эта связь - для атомов тяжелых элементов и элементов с большим числом валентных электронов.

Промежуточная связь – сочетание LS и jj связи для разных групп электронов в атоме.

В связи с рассмотрением системы квантовых чисел вернемся к квантовым числам молекул. Часть этого материала уже рассмотрена выше.

Энергия молекулы Е = Е_эл. + Е_кол. + Е_вр.

Е_эл. >> Е_кол. >> Е_вр.

Примерное расстояние между уровнями:

∆Е_эл. ≈ 1 – 10 эВ.

∆Е_кол. ≈ 0,01 – 1 эВ.

∆Е_вр. ≈ 10^-3 – 10^-2 эВ.

Все эти энергии квантованы и для их обозначения вводятся квантовые числа.

,

где q = 0, 1, 2… - колебательное квантовое число; ω₀ – частота колебаний.

(При q = 0 - энергия нулевых колебаний при комнатной температуре). Правила отбора: ׀Δq׀ = 1

Энергия вращения относительно общего центра масс

где I – момент инерции молекулы; К = 0, 1, 2… вращательное квантовое число.

Вращательный момент количества движения молекулы

.

Помимо К вращательное движение характеризуется числом М_к, которое определяет проекцию на выделенное направление z

(М_к меняется от К до –К).

Правила отбора для числа К: ∆К = 0, ±1.

Движение молекулы характеризуется также орбитальным и спиновым квантовыми числами. (Подробно на этом не останавливаемся). Орбитальное квантовое число молекулы обозначают Λ = 0, 1, 2, … ,оно характеризует проекцию орбитального момента на ось молекулы.

Обозначения термов: Λ = 0 Σ

Λ = 1 Π

Λ = 2 ∆

Спиновое квантовое число молекулы S, внутреннее квантовое число Ω.

Символика молекулярного терма ^{2s + 1}Λ_Ω.