Книги и конспекты / Шпоры / 21

21. Замыкание множества. Замкнутое множество. Важнейшие замкнутые классы. Лемма о несамодвойственной функции.

1. Система P2 — множество всех булевых функций — является полной системой.

О п р е д е л е н и е 60. Пусть M — некоторое подмножество функций из P2. Замыканием M называется множество всех булевых функций, представимых в виде формул через функции из множества M. Замыкание множества M обозначается

через [M].

П р и м е р 29.

1)M = P2. Очевидно, [M] = P2.

2)M = {1, x1 +x2}. Замыканием этого множества будет класс L всех линейных функций, т.е. функций, имеющих вид

f(x1, ..., xn) = c0 + c1x1 + ... + cnxn( mod 2), где ci = 0 1 (i = 0, 1, ..., n).

Отметим некоторые свойства замыкания:

1)[M] M;

2)[[M]] = [M];

3)если M1 M2, то [M] [M];

4)[M1 M2] [M1] [M2].

О п р е д е л е н и е 61. Множество M называется замкнутым, если [M] = M.

1)Класс M = P2 является замкнутым классом.

2)Класс M = {1, x1 + x2} не замкнут.

3)Класс L замкнут, так как линейная комбинация линейных функций является линейной функцией. Система функций M является полной, если [M] = P2.

Перечислим некоторые важнейшие замкнутые классы в P2.

1. Обозначим через T0 класс всех булевых функций f(x1, ..., xn), сохраняющих константу 0, т.е. функций, для которых выполнено равенство f(0, . . . , 0) = 0.

Легко видеть, что функции 0, x, x1&x2, x1 x2, x1 + x2 принадлежат классу T0, а функции 1, 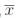не входят в T0. Поскольку таблица для функций f из класса T0 в первой строке содержит значение 0, то в T0 содержится ровно

булевых функций, зависящих от переменных x1, ..., xn.

Покажем, что T0 — замкнутый класс. Так как T0 содержит тождественную функцию, то для обоснования замкнутости T0 достаточно показать, что функция

Φ = f(f1, . . . , fm)

принадлежит классу T0, если f, f1, . . . , fm принадлежат классу T0. Последнее вытекает из цепочки равенств

Φ(0, ..., 0) = f(f1 (0, ..., 0), ..., fm (0, ..., 0)) = f(0, ..., 0) = 0.

2. Обозначим через T1 класс всех булевых функций f(x1, ..., xn), сохраняющих константу 1, т.е. функций, для которых выполнено равенство f(1, ..., 1) = 1.

Легко видеть, что функции 1, x, x1&x2, x1 x2 принадлежат классу T1, а функции 0, 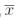не входят в класс T1. В силу того, что класс T1 состоит из функций, двойственных функциям из класса T0, нетрудно перенести результаты о классе T0 на класс T1. Класс T1 содержит функций, зависящих от переменных x1, ..., xn, и является замкнутым классом.

3. Обозначим через S класс всех самодвойственных функций, т.е. функций f из P2, таких, что f = f.

Очевидно, что самодвойственными функциями будут x, 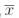. Менее тривиальным примером самодвойственной функции является функция h(x1, x2, x3) = x1x2 x1 x3 x2 x3:

h ( x1, x2, x3) = (x1 x2)( x1 x3)( x2 x3) = x1 x2 x1 x3 x2 x3 = h x1, x2, x3).

Для самодвойственных функций имеет место тождество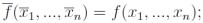

иначе говоря, на противоположных наборах 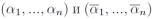самодвойственная функция принимает противоположные значения. Отсюда следует, что самодвойственная

функция полностью определяется своими значениями на половине строк таблицы, задающей функцию. Поэтому

число самодвойственных функций, зависящих от переменных (x1, ..., xn), равно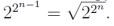

Докажем теперь, что класс S замкнут. Поскольку класс S содержит тождественную функцию, достаточно показать, что функция

Φ = f(f1, . . . , fm)

является самодвойственной, если f, f1, . . . , fm самодвойственны. Последнее устанавливается непосредственно: Φ = f ( f1*, . . . , fm*) = f(f1, . . . , fm) = Φ.

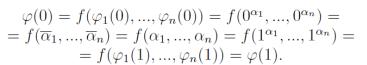
Лемма 7. (о несамодвойственной функции). Если f(x1, ..., xn) S, то из нее путем подстановки функций x и 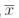можно получить константу.

Д о к а з а т е л ь с т в о. Так как f S, то найдется набор

(α1, ..., αn), такой, что

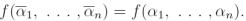Рассмотрим функции ϕi(x) = xαi (i = 1, ..., n) и положим

ϕ(x) = f(ϕ1(x), . . . , ϕn(x)).

Мы имеем

Лемма доказана.