Операции над детерминированными функциями.

Пусть детерминированная ф-ия F задана системой (2) и каждая из функций и всюду определенные функции к-значной логики.

Будем рассматривать ф-ию f как элемент мн-ва

Обозначим схему реализующую ф-ию f.

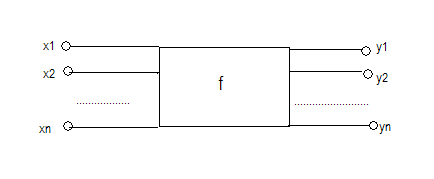
Схему будем изображать в виде прямоугольника с n входами и m выходами. Входы изображаются в виде стрелок исходящих из входных полюсов. Выходы - стрелки из выходных. Полюса- кружочки.

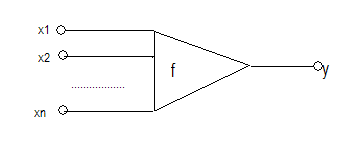
Если m=1 то схему реализующую ф-ию.f иногда изображают в виде треугольника с n входными и одним выходным полюсами.

Считаем что в каждый момент времени t=1, 2 на i-ый вход поступает входной символ а на j-ом выходе выдается значение.

Операции

1) Операция отождествление 2-х или > или числа входных переменных в ф-ии f

В результате этой операции происходит отождествление в схеме соотв-х этим переменным входных полюсов.

2) Операция удаление некоторой выходной переменной . Данная операция эквивалентна выбрасыванию из системы (2) уравнения И удаление из схемы выходного канала и полюса .