Монотонные функции.
Опр.
из того что
включено
в
Примеры:
0,1,x,
,
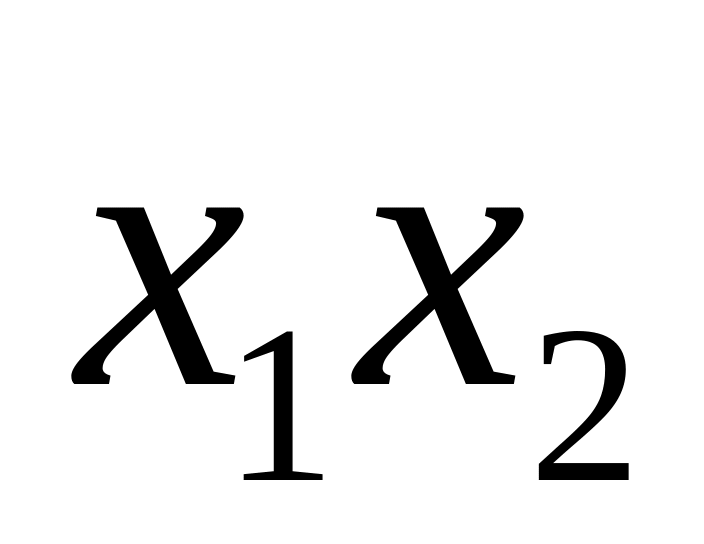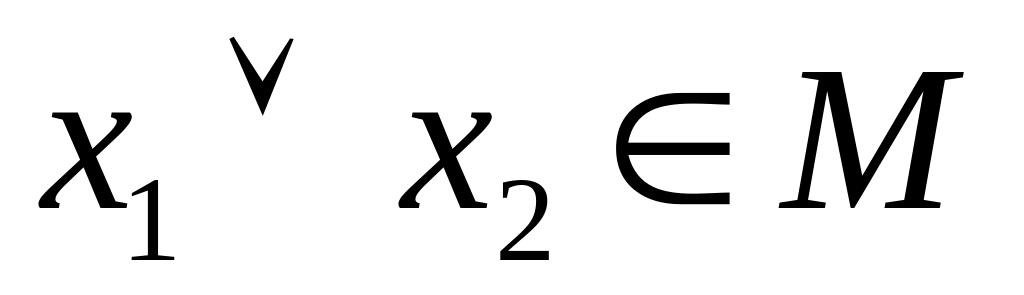
Способы выявления монотонности
Эквивалентные преобразования. Если функция содержит только конъюнкцию и дизъюнкцию, то она монотонна.
С помощью таблицы истинности.
М – замкнутый класс
Док-во. Надо доказать: суперпозиция класса М совпадает с самим классом М.
Рассмотрим функцию
- суперпозицию монотонных функций. Т.е.
таким образом, надо показать, что если
то и
Пусть G определена на
наборе переменных
Тогда
будет
определена на наборе
И
т.д.
будет
определена на наборе
Возьмем две оценки списка переменных
и обозначим их
и
Причем:
Аналогичным образом получим наборы
и
,
и
…
и
Кроме того
,
,....
Таким образом в силу того что функции
F монотонные и
получим:
Тогда если составить наборы из соответствующих наборов функций то будет иметь место следующее соотношение
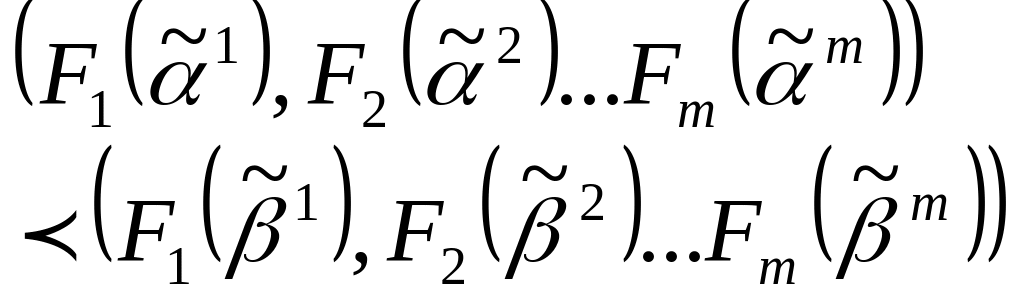
А в силу того что функция F монотонная получим что
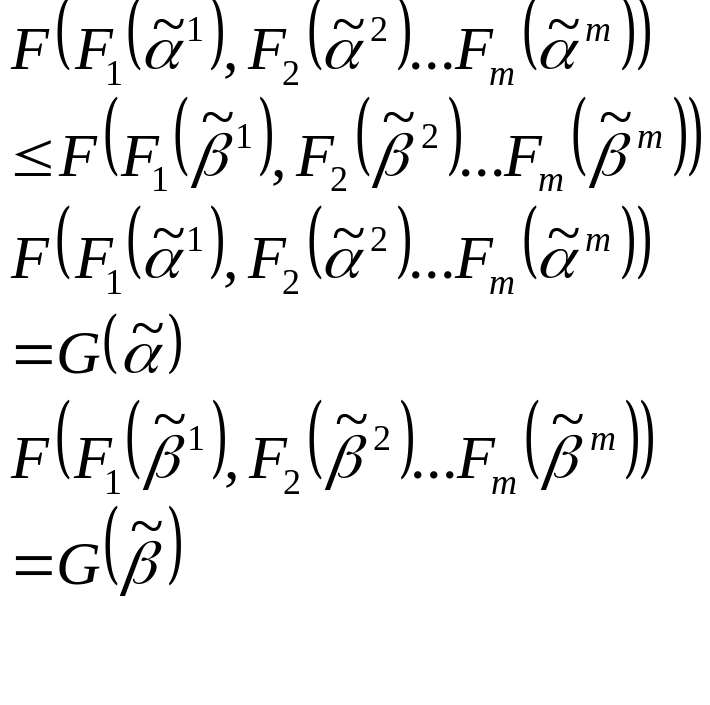
Таким образом
Таким образом в силу произвольности выбора функции F мы доказали что суперпозиция класса М совпадает с самим классом М.
Лемма о несамодвойственной функции.
Если функция
то
из нее путем подстановки
и
можно получить несамодвойственную
функцию одного переменного – константу
Док-во.
Если
, то
двоичный набор
Рассмотрим подобранные функции которые конструируются следующим образом
Рассмотрим
Рассмотрим значение
при
и
Если
,
Если
, то
Если
, то
Если
, то
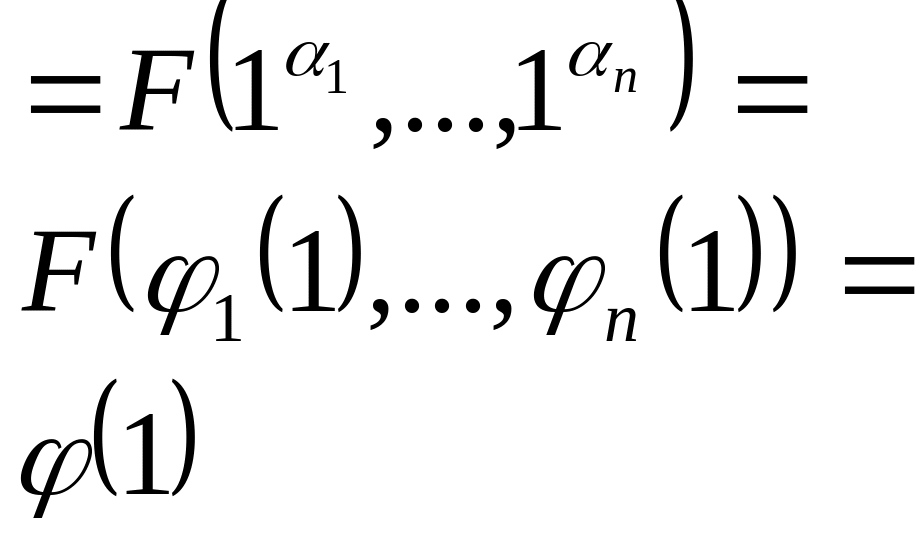
Таким образом
–константа.
Лемма о немонотонной функции
Если функция
То из нее путем подстановки
можно получить немонотонную функцию
одного переменного -
Док-во
1 этап. Покажем что если
, то
два двоичных набора
и
и
1 случай доказывать ничего не надо
2 случай
это значит, что
Покажем что можно выбрать другие наборы и они будут соседними
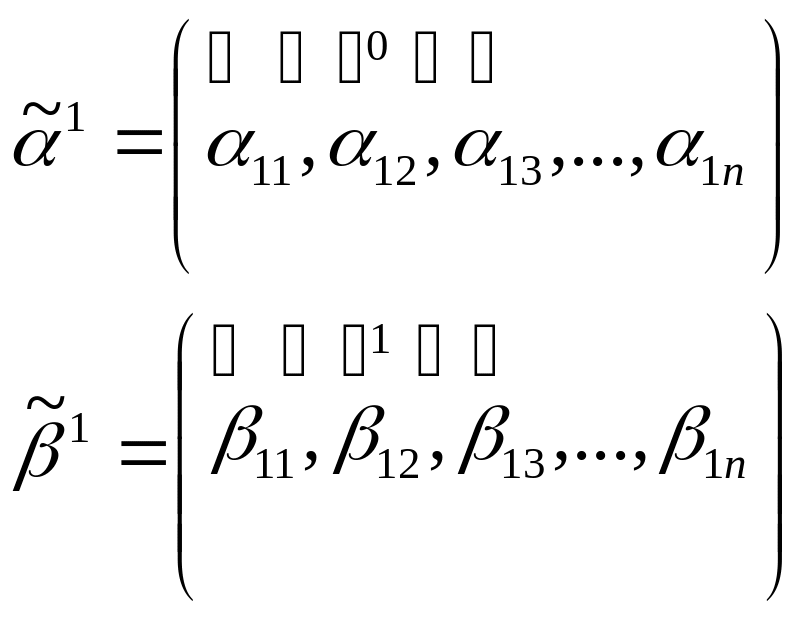
Между
и
Мы можем взять
промежуточных набора, причем таких что
и
Значит хотя бы для одной пары промежуточных
наборов ( обозначим их
и
) будет выполняться неравенство:
Пусть данные наборы имеют соседство по i-ой координате
2этап
Рассмотрим функцию, которая конструируется следующим образом
Рассмотрим значения при и
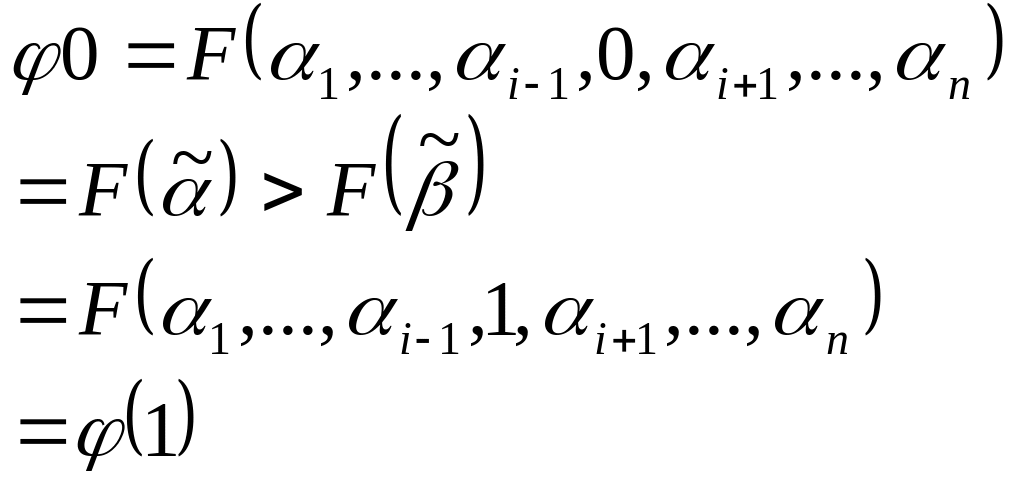
Учитывая, что мы работаем с булевыми функциями, это становится возможным только если
а
Следовательно
.
Лемма о нелинейной функции
Если функция
То из нее путем подстановки
можно получить не линейную функцию -
Док-во
Для любой функции можно построить полином Жегалкина, притом единственный. Построим его для функции F.
Так как
то в полиноме найдется член, содержащий
не менее двух множителей. Без ограничения
общности можно считать, что среди этих
множителей присутствуют
и
. Тогда можно преобразовать полином
следующим образом.
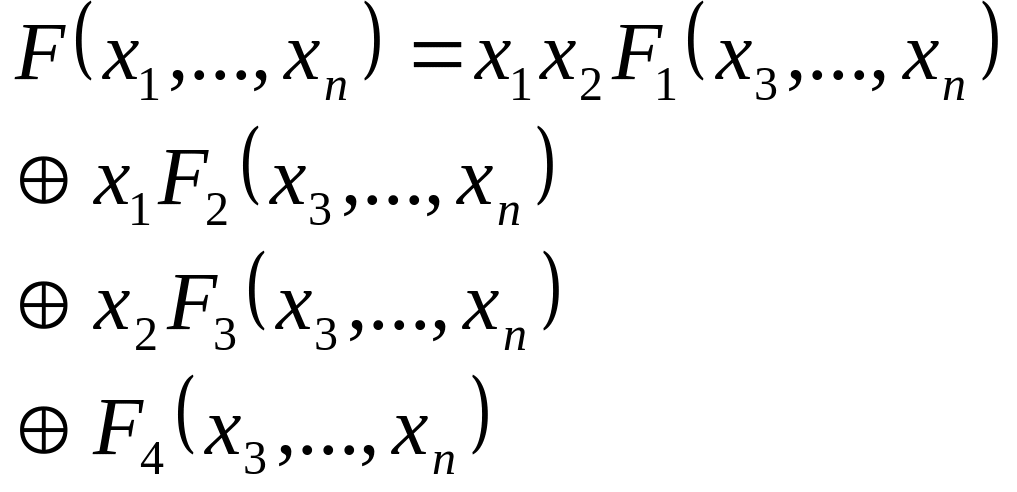
Очевидно, что
так как
Выберем такой двоичный набор
на котором
Пусть функция
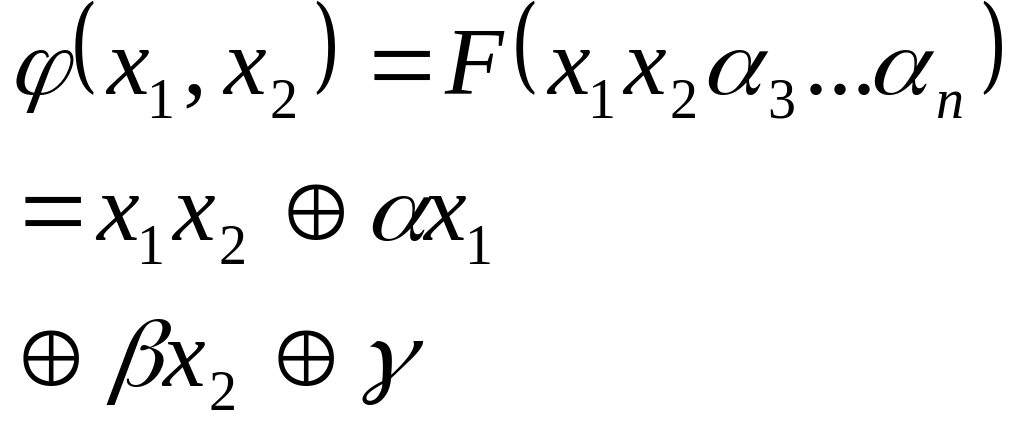
Рассмотрим функцию которая конструируется следующим образом
Подставим в функцию
Формулу для функции
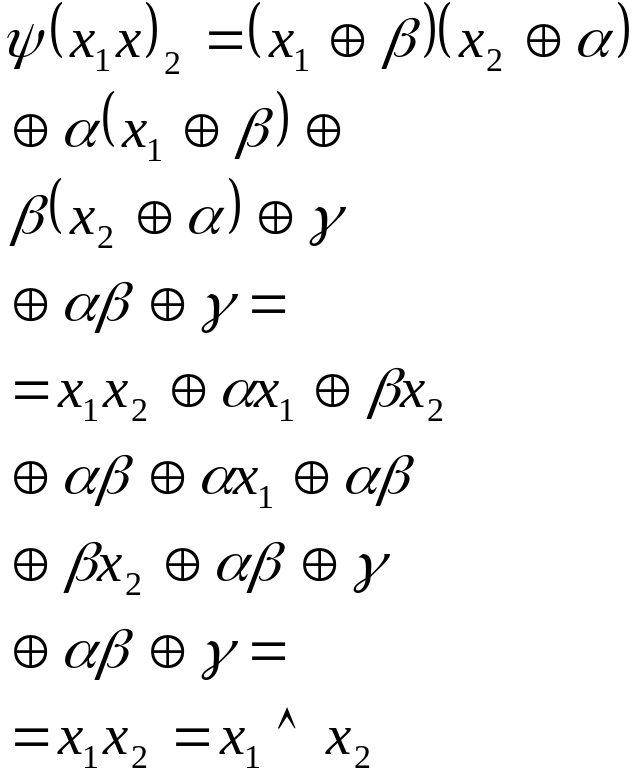
Лемма доказана.
Таблица Поста. Алгоритм построения базисов
Дана система функций
Таблица Поста:
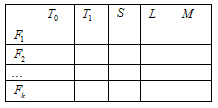
На пересечении класса и функций ставится “+” если функция принадлежит классу. Иначе – “-”