Остовное дерево. Минимальное остовное дерево. Алгоритм Краскала
Остовное дерево - это подграф основного графа, который состоит из тех же вершин, но не всех рёбер(так, чтобы не образовывались циклы).
Минимальное остовное дерево - это такое остовное дерево, где сумма весов его рёбер минимальна.
Алгоритм:
Сортируем рёбра по возрастанию веса рёбер.
Соединяем вершины с ребром минимального веса.
(Первая итерация алгоритма)Повторяем шаг 2 либо когда мы соединяем две изолированные вершины, либо когда мы соединяем группу вершин из предыдущей итерации с любой другой изолированной вершиной(вершина без рёбер). Соединять вершины в группе соединенных вершин, безусловно, нельзя.
(Вторая итерация)Снова рассматриваем рёбра по возрастанию таким образом, чтобы соединить рёбрами уже разные группы вершин
Алгоритмы поиска путей. Флойда-Уоршелла
Алгоритм Флойда-Уоршелла – один из алгоритмов поиска путей. В нём используется матрица смежности. Матрица смежности – это матричный способ представления графа, в которой указаны узлы и веса рёбер между ними.
Берется одна из вершин в качестве дополнительной и подставляется в формулу, которая гласит, что если путь через новую вершину короче, чем через старый вариант, то необходимо поменять [i][j]-ое значение в матрице смежности на то, которое получилось. Если повторять итерации с новыми дополнительными вершинами, то можно найти более сложные пути. Для полной работы алгоритма необходимо подставить все вершины.
Алгоритмы поиска путей. Форда-Фалкерсона
С помощью алгоритма Фалкерсона можно оценить максимальную пропускную способность сети представленной направленным графом.
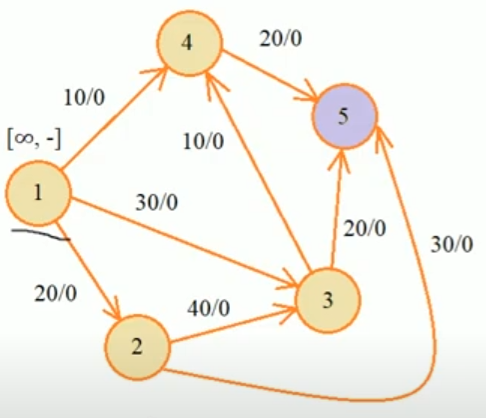
Алгоритм:
Величина дуг пересчитывается следующим образом:
где:
A - значение перед дробью
B - значение после дроби
f - Поток
шаги алгоритма:
Выбираем вершины истока и стока. Нюанс: Выходной поток равен наименьшему значению из сумм весов рёбер исходящих из истока и сумм весов рёбер входящих в сток.
Формируем множество вершин, с которыми имеются положительные остаточные веса дуг (вершины, в которые еще что-то может затекать). Если множество пустое - переходим к шагу 4
Во множестве S (вершин) находим вершину, к которой идет дуга с наибольшим остаточным весом. Формируем для нее метку в формате ‚ где - значение остаточного потока к этой вершине от рассматриваемой К-й вершины. Выбираем найденную вершину как текущую. Если она не является стоком, то переходим к шагу 2. Если она является конечной (стоком), то переходим к шагу 5.
Откат назад (если нужно). Если К = 1, то движение пока невозможно (шаг 6). Если К<1, то переходим к предыдущей вершине, удаляя текущую из списка возможных вершин
Для найденного маршрута пересчитываем остаточные величины потоков. Возвращаемся на 1 шаг
Подводим итог. Максимальный поток - сумма загрузки дуг, выходящих из истока.
Алгоритмы поиска путей. Дейкстры
Суть алгоритма заключается в поиске всех кратчайших маршрутов от одной вершины графа до всех остальных. Работает только с положительными весами.
Алгоритм:
Определяемся со стартовой вершиной и составляем матрицу весов.
На первой итерации в первую взятую вершину записываем 0, т.к. расстояние из этой вершины до самой себя равно 0.
На второй итерации мы к значению первой вершины прибавляем вес рёбер других вершин, соединенных с первой, то есть 0 + вес. Записываем полученные значения в матрицу(если первая вершина не соединена с конкретной вершиной, то записываем в матрицу бесконечность)
На третьей итерации берем вершину с минимальным весом в таблице. Смотрим в какую вершину мы можем пройти и складываем вес узла с минимальным весом и вес узла, в который мы стремимся попасть. Далее сравниваем полученное значение с предыдущим в таблице и если оно меньше, то записываем его в таблицу, иначе оставляем предыдущее значение. Нюанс: Если веса рёбер в таблице одинаковы, то берём любую вершину из этих.
Повторяем до тех пор, пока не пройдем все вершины.