
Инд. мат. стат
.DOCXМИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ УКРАИНЫ
ОДЕССКИЙ НАЦИОНАЛЬНЫЙ ЭКОНОМИЧЕСКИЙ УНИВЕРСИТЕТ
Кафедра маркетинга
Индивидуальное задание ЭММ
Вариант 5
Выполнила:
Одесса – 2021
Задание 1.1
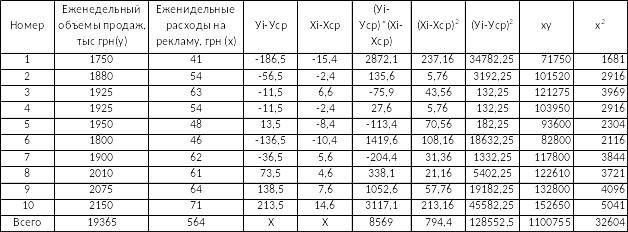
В таблице 1 приведены еженедельные расходы на рекламу (Х) и еженедельные объемы продаж (У).
Таблица 1
Вопросы:
а) существует ли значимая взаимосвязь между расходами на рекламу и объемом продаж?
б) определить уравнение линейной модели с помощью таблиц (без компьютера – с калькулятором).
в) определить уравнение линейной модели с помощью пакета «Анализ данных». Оценить точность, надежность и адекватность полученной модели.
г) определите объем продаж при расходах на рекламу в 55 грн.
Формулы, которые использовались при подсчетах в заданиях 1.1 и 1.2


![]()
![]()
А) Существует ли значимая взаимосвязь между расходами на рекламу и объемом продаж?
Были найдены следующие показатели:
Gy= 113,3809949
Gx= 8,912911982
Rxy= 0,85
Коэффициент корреляции Пирсона является положительным числом и > 0,7, что свидетельствует о том, что между еженедельными расходами на рекламу и еженедельными объемами продаж существует тесная прямая взаимосвязь. Чем больше расходы на рекламу, тем больше объем продаж.
Б) Определить уравнение линейной модели с помощью таблиц (без компьютера – с калькулятором).
Были найдены следующие показатели
b1= 10,7867573
b0=1328,126888
у=1328,127+10,78676х
В) С помощью пакета «Анализ данных» и функции «Регрессия» получили выводы итогов
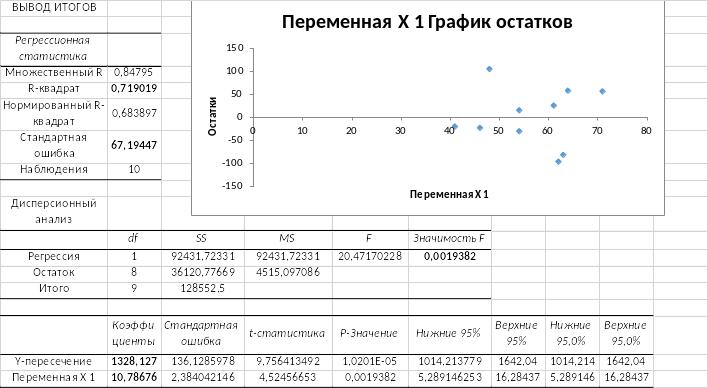
F-критерий меньше уровня значимости альфа в 0,05, что говорит о том, что модель надежна.
Модель достаточно точна. В данном случае коэффициент детерминации показывает, что 71,9% вариации результативного показателя (еженедельные объемы продаж) объясняется вариацией признака (еженедельные затраты на рекламу), а остальные 28,1% зависят от факторов, не вошедших в модель.

Модель является адекватной, так как множественный R меньше 0,3.
Г) Определите объем продаж при расходах на рекламу в 55 грн.
Были найдены следующие показатели:
x= 55
y= 1921,39854
При уровне еженедельных расходов на рекламу в объеме 55 грн, еженедельный объем продаж составит 1921,39854тыс. грн.
Задание 1.2
В таблице 2 приведены сведения о времени, затраченном на обслуживание покупателей в супермаркете, и соответствующих объемах покупок.
Таблица 2

Вопросы:
а) существует ли значимая взаимосвязь между временем обслуживания и объемом покупок?
б) определить уравнение линейной модели с помощью таблиц (без компьютера – с калькулятором).
в) определить уравнение линейной модели с помощью пакета «Анализ данных». Оценить точность, надежность и адекватность полученной модели.
г) определить объем покупок при времени обслуживания в 1, 3 и 5 минут.
А) Существует ли значимая взаимосвязь между временем обслуживания и объемом покупок?
Были найдены следующие показатели:
Gx = 1,655173707
Gy = 146,5918142
Ryx = 0,967074333
Б) Определить уравнение линейной модели с помощью таблиц.
Были найдены следующие показатели:
b1=85,64972989
b0=9,693750913
y= 9,693751+85,64973x
В) С помощью пакета «Анализ данных» и функции «Регрессия» получили выводы итогов
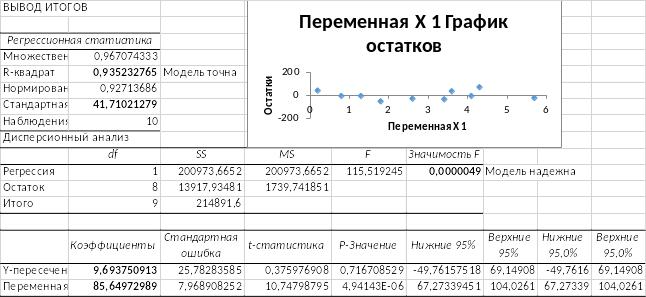
В данном случае модель достаточно точна, стандартная ошибка по значению мала, а коэффициент детерминации показывает, что 93,5% вариации результативного показателя (объем покупок) объясняется вариацией признака (затраты на обслуживание), а остальные 6,5% зависят от факторов, не вошедших в модель.
F-критерий меньше уровня значимости альфа в 0,05, что говорит о том, что модель надежна.

Модель является адекватной, так как множественный R меньше 0,3.
Г) Определить объем покупок при времени обслуживания в 1, 3 и 5 минут.
y= 9,693751+85,64973x
х1=1
у1= 95,343481
х2=3
у2= 266,642941
х3=4
у3= 437,942251
При времени обслуживания в 1 минуту объем покупок будет составлять 95,34 грн, при 3-ех минутах - 266,64грн, при 5-ти минутах - 437,94грн.
Задание 2.1
В таблице 3 приведены объемы продаж корпорации NOVAK за период с 1998 по 2014 год. Подобрать наилучший тренд, описывающий динамику данных, среди следующих функций: линейная; квадратичная (с линейной составляющей и без нее); логарифмическая; степенная; экспоненциальная. Привести графики по подобранным моделям. По лучшим моделям получить прогноз на 5 лет.
Таблица 3

Были построены следующие графики, описывающие динамику данных:
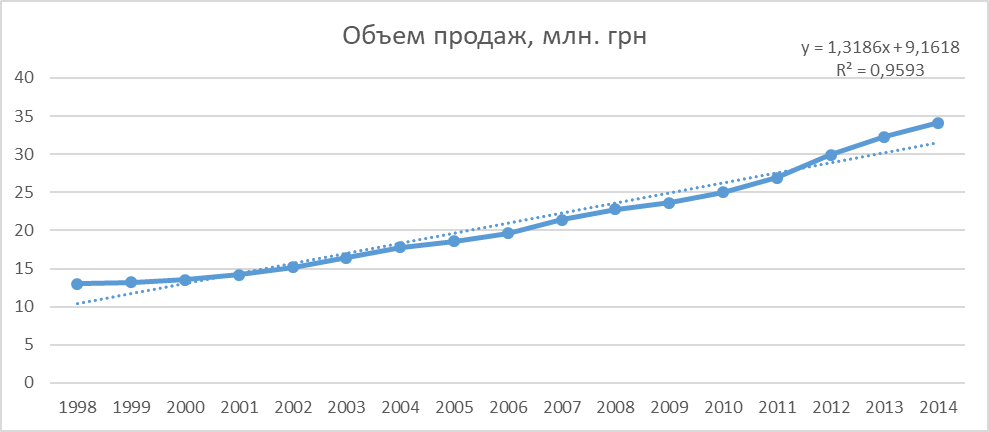
Рис. 1. Линейный тренд
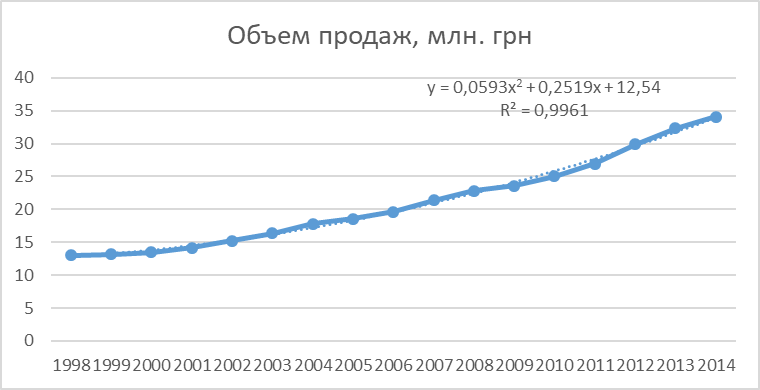
Рис. 2. Параболический тренд

Рис. 3. Логарифмический тренд

Рис. 4. Степенной тренд
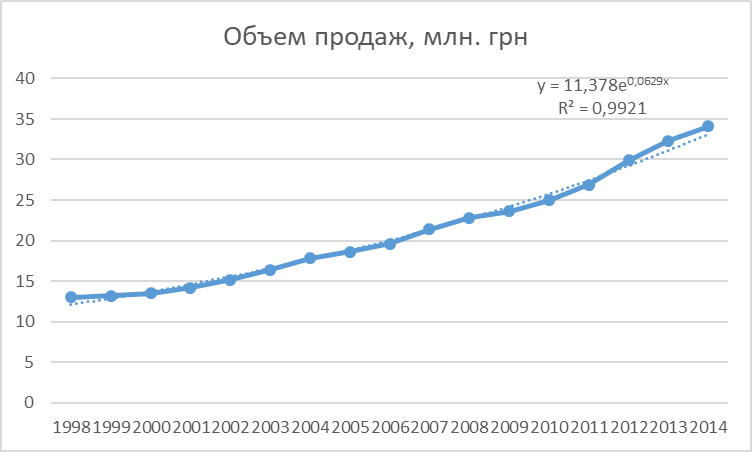
Рис. 5. Экспоненциальный тренд
Далее было построено прогнозирование на основе каждого из трендов на период с 2015 года по 2019 год. Данные представлены в таблице 4.
Таблица 4
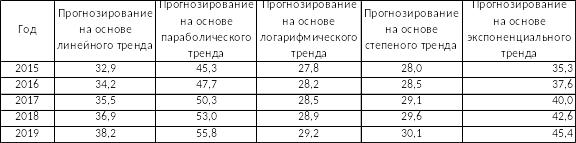
Вывод: Параболический и экспоненциальный тренды являются наиболее точным. Поэтому при условии, что тенденция изменения объема продаж сохранится в будущем можно спрогнозировать, что в 2015 году он составит 45,3 млн. Грн, в 2016 год - 47,7 млн. грн.
Задание 2.2
Выбрать любой из макроэкономических показателей Украины. Подобрать наилучший тренд, описывающий динамику данных, среди следующих функций: линейная; квадратичная (с линейной составляющей и без нее); логарифмическая; степенная; экспоненциальная. Привести графики по подобранным моделям. По лучшим моделям получить прогноз.
Объем реализованной продукции многолетних культур, тыс грн. В Украине (2010-2019).
Таблица 5

Были построены следующие графики, описывающие динамику данных:

Рис. 6. Линейный тренд

Рис. 7. Параболический тренд

Рис. 8. Логарифмический тренд
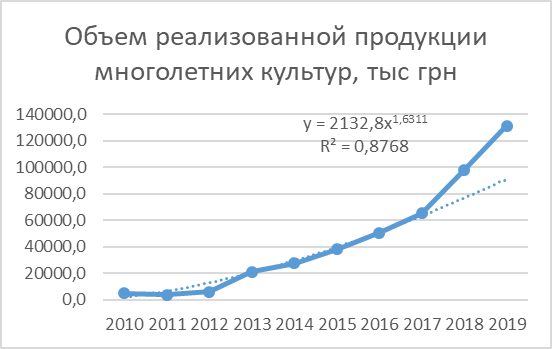
Рис. 9. Степенной тренд

Рис. 10. Экспоненциальный тренд
Далее было построено прогнозирование на основе каждого из трендов на период с 2020 года по 2024 год. Данные представлены в таблице 5.
Таблица 5
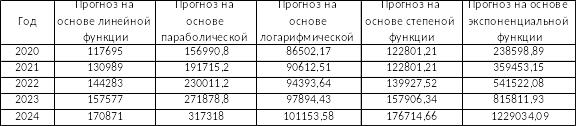
Вывод: параболический тренд является наиболее точным. Поэтому при условии, что тенденция реализованной продукции сохранится в будущем можно спрогнозировать, что в 2020 году они составят 156990,8 тыс.грн, а в 2021 году – 191715,2 тыс.грн.
Задание 3
Вопросы:
1. Вычислите сезонные индексы для каждого квартала.
2. Получите прогноз авиаперевозок на 3 года с учетом сезонности.
3. Постройте графики исходных данных, полученной модели и прогноза.
1. Вычислите сезонные индексы для каждого квартала
Были найдены следующие показатели сезонных индексов для каждого квартала:
1 квартал - 0,90
2 квартал - 1,05
3 квартал - 1,18
4 квартал - 0,87
Индексы сезонности, рассчитанные для каждого квартала свидетельствуют, что объемы пассажира потока авиакомпании увеличиваются во 2 и 3 квартале и снижаются в 1 и 4.
2. Получите прогноз авиаперевозок на 3 года с учетом сезонности
С помощью пакета «Анализ данных» и функции «Регрессия» получили выводы итогов
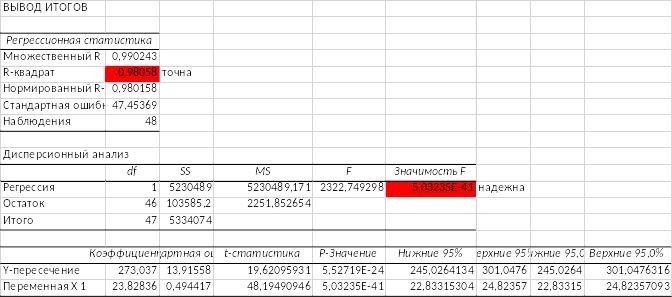
Модель является надежной, так как –критерий Фишера меньше уровня значимости альфа 0,05. Поскольку R-квадрат близок к 1, модель точна.

Модель является неадекватной, так как множественный R больше 0,3.
Были получены следующие уравнения:
у=b0+b1x
y=273,037+23,82836х
В таблице 6 были получены прогнозы с поправкой на сезон и с учетом сезонности.
Таблица 6
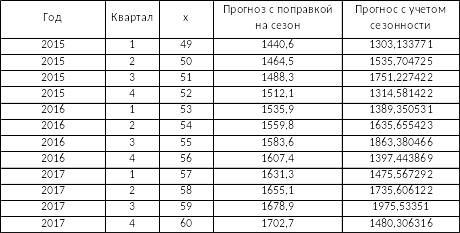
3. Постройте графики исходных данных, полученной модели и прогноза

Рис. 11. График объема авиаперевозок и объема перевозок с поправкой на сезон
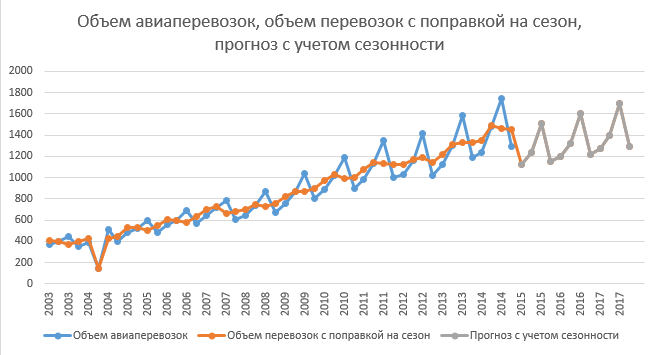
Рис. 12. График объема авиаперевозок, объема перевозок с поправкой на сезон и прогноз с учетом сезонности
Задание 4
В таблице представлены данные. В качестве У (объясняемой) рассматривается стоимость одной страницы полноцветной рекламы. Объясняющими переменными будут Х1, читательская аудитория (планируемая в тысячах человек), Х2, процент мужчин среди планируемой аудитории, и Х3, медиана дохода семьи. Размер выборки n=55.
Вопросы:
1. Построить корреляционную матрицу;
2.Получить модель зависимости стоимости страницы рекламы от приведенных факторов;
3. Оценить модель на точность, надежность и адекватность;
4. Какие переменные значимо влияют на стоимость рекламы? Какие – нет? Если есть переменные не влияющие на стоимость страницы реклама – удалить их из модели.
5. Получить прогнозы.
1. Построим корреляционную матрицу. Данные представлены в таблице 7.
Таблица 7

Существует тесная взаимосвязь между тарифом размещения рекламы и планируемой аудиторией журнала, взаимосвязь прямая. Чем больше аудитория, тем выше тариф. С двумя другими факторами (процент мужчин и доход) тариф на размещение рекламы связан слабо.
Между процентом мужчин и медианой дохода семьи существует также средняя взаимосвязь.
С помощью пакета «Анализ данных» и функции «Регрессия» получили выводы итогов.
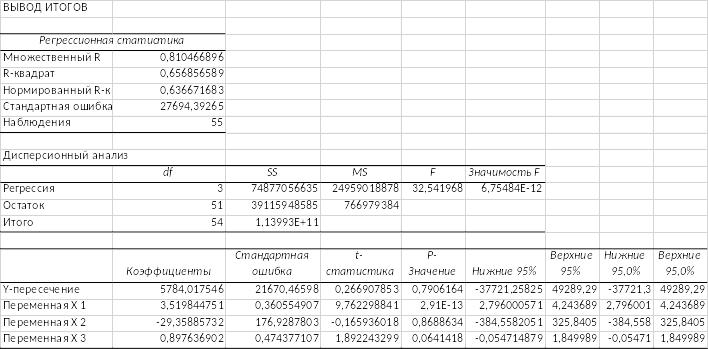
Благодаря выводу итогов, мы видим, что переменная х2 не влияет на стоимость страницы рекламы, соответственно можем удалить ее из модели.
Вывод: Модель точна. 65,7 % вариации тарифа на рекламу объясняется планируемой аудиторией и медианными доходами семьи, остальные 34,3% вариации тарифа объясняются факторами, не вошедшими в модель.
Модель надежна, так как F-критерий Фишера меньше ур. Альфа 0,05.

Модель является адекватной, так как множественный R меньше 0,3.

![]()

При увеличении планируемой аудитории на 1000 чел. Тариф на рекламу вырастет на 3,52 коп. При увеличении медианы дохода семьи на 1 грн - тариф на рекламу вырастет на 85 коп.
Вывод: модель достаточно точна на 65, 7% вариация тарифа на рекламу объясняется планируемой аудитории и медианными доходами семьи. Остальные 34,3% вариации тарифа объясняются факторами, не вошедшими в модель. Критерий Фишера меньше значения альфа 0,05, что говорит, что модель надежна.

Модель является адекватной, так как множественный R меньше 0,3.
Найдем уравнение регрессии:
у=6765,062+3,514824х1+0,853789х3
Допустим, что
x1 = 5000
х3= 25000
Тогда х1=45683,91532
Вывод: при планируемой аудитории в 5000 тыс. чел, и медианы дохода семьи в 25000 грн, можно спрогнозировать, что тариф одной страницы рекламы будет 45683,91 грн.
