
Экспериментальные методы исследований. Калинин Ю.Е
.pdf
i |
|
|
|
|
U |
|
|
|
|
|
. |
(6.42) |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||||||
|
|
|
r |
|
|
r |
|
|||||
|
|
r |
1 |
r |
|
L2 |
1 |
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
N |
r2 |
1 |
|
N |
r2 |
|
|||
|
|
|
|
|
|
|
|
|||||
Тогда максимальные значения магнитной индукции и напряженности намагничивающего поля можно рассчитать по следующим формулам:
Bm |
|
iLx |
2 |
|
, |
(6.43) |
|||
|
S |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
H |
|
|
wi |
2 |
, . |
(6.44) |
|||
m |
|
|
|||||||
|
|
|
dcp |
|
|
|
|||
|
|
|
|
|
|
|
|||
Рассмотренная нами схема моста с переменной индуктивностью дает небольшие ошибки измерения только в том случае, если индуктивности, включенные в плечи моста, имеют значение не меньше 10 МГн.
Схема моста с переменной емкостью. Схема этого моста показана на рис. 6.11. Два противоположных плеча моста имеют только активные сопротивления r1 и r2. Два других плеча моста СВ и AD обладают реактивными и активными сопротивлениями.
Проводя преобразования, аналогичные случаю, рассмотренному выше, получим формулы для определения rx и Lx:
r |
r1r2 |
, |
|
|
|
|
|||
x |
|
rN |
|
|
|
|
|
|
|
|
Lx CN r1r2 . |
(6.45) |
||
Рассмотренные мостовые схемы применяют для определения магнитных характеристик в магнитных полях промышлен-
321
ной частоты. Погрешность измерений мостовых схем составляет около 3 %.
6.5.2.3. Потенциометрический метод измерения магнитных характеристик в переменных полях
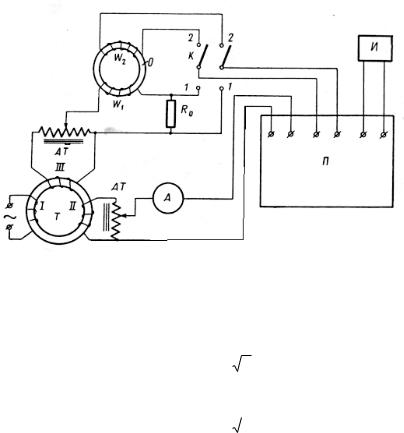
Точным и простым методом измерения магнитных характеристик в магнитных полях промышленной частоты является потенциометрический метод, который основывается на измерениях ЭДС во вторичной обмотке образца и тока в намагничивающей цепи. Принципиальная схема установки для измерения магнитной индукции с потенциометром переменного тока показана на рис. 6.12. На образце О есть две обмотки: намагничивающая W1 и измерительная W2. Ток в обмотке W1 регулируют автотрансформатором AT, на который подается напряжение с разделительного трансформатора Т, имеющего три обмотки. Одна из этих обмоток (I) служит для включения трансформатора в сеть питания, вторая (II) подает напряжение на потенциометр П и третья (III) используется для намагничи-вания образца. Для определения точек основной кривой индукции нужно знать падение напряжения U1 на эталонном сопротивлении R0 и ЭДС Е2 в измерительной обмотке W2, причем эти величины следует определять при нескольких значениях тока в намагничивающей цепи. Значение величин U1 и R0 дает возможность рассчитать величину силы тока в намагничивающей обмотке W1. По полученным значениям Е2 во вторичной цепи и значениям тока в намагничивающей обмотке образца рассчитывают индукцию образца, напряженность магнитного поля, магнитную проницаемость и потери.
Если вторичная обмотка образца незамкнута, то реактивная составляющая полного тока будет находиться в фазе с магнитным потоком, который существует в исследуемом образце, при этом вектор потока сдвинут на 90° по отношению к вектору ЭДС вторичной обмотки цепи. Реактивную составляющую i полного тока определяют как его проекцию на направление
322
вектора магнитного потока, а активную составляющую ia полного тока выражают через проекцию его на направление, противоположное э.д.с. во вторичной цепи Е2. Магнитную индукцию исследуемого образца рассчитывают по формуле (6.38). Так как напряженность магнитного поля представляется в комплексном виде, то действительную и мнимую части вектора напряженности магнитного поля записывают в виде
Рис. 6.12. Схема установки с потенциометром переменноготока:
О – исследуемый образец; W1 – намагничивающая обмотка; W2 – измерительная обмотка; Т – трансформатор; I, II, III – обмотки трансформатора тока; АТ – автотрансформатор
H д |
|
w1i |
2 |
, |
(6.46) |
||
|
l |
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
w1iа |
2 |
|
|
(6.47) |
H мн |
|
|
|
|
, |
||
|
l |
|
|
||||
|
|
|
|
|
|
|
|
323
где l - длина средней магнитной линии образца, i - реактивная составляющая полного тока, ia - активная составляющая полного тока.
Комплексную магнитную проницаемость определяют по формуле
1 |
j 2 |
|
|
|
|
|
Bm |
|
. |
(6.48) |
||||||||||||
|
0 H |
д jH |
мн |
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Составляющие комплексной |
магнитной |
|
проницаемости |
|||||||||||||||||||
имеют вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
1 |
|
|
|
|
|
|
Bm |
|
|
|
Н д , |
|
|
(6.49) |
||||||||
|
|
H 2 |
Н 2 |
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
0 |
|
|
д |
|
|
мн |
|
|
|
|
|
|
|
||
2 |
|
|
|
|
|
|
|
Bm |
|
|
|
Н мн . |
|
|
(6.50) |
|||||||
|
|
|
H |
2 |
Н |
2 |
|
|
||||||||||||||
|
|
|
|
|
0 |
|
|
|
д |
|
|
|
|
мн |
|
|
|
|
|
|
|
|
Амплитудная магнитная проницаемость равна |
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
Bm |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
(6.51) |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
0 |
|
|
H 2 |
Н 2 |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
д |
|
|
|
мн |
|
|
|
|||
Ошибки при определении магнитных характеристик потенциометрическим методом составляют около 3 %.
6.5.2.4. Измерение магнитной проницаемости
ипотерь на частотах 50 кГц — 10 МГц
Вобласти высоких частот для измерения магнитной проницаемости используют резонансный метод, принципиальная схема которого изображена на рис. 6.13.
324
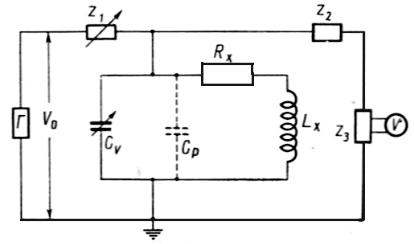
Рис. 6.13. Схема резонансного метода для определения комплексной магнитной проницаемости в слабых полях:
Г - генератор, Cv - переменная емкость для настройки в резонанс, Lx - индуктивность катушки образца,
Rx - эквивалентное сопротивление, V - вольтметр, Cp - собственная емкость катушки,
Z1, Z2, Z3 - реактивные сопротивления
На исследуемый образец, который имеет форму тороида или рамки, наматывают несколько витков медной проволоки. Колебательный контур связан с генератором Г через большое реактивное сопротивление z1. При помощи этого сопротивления достигается слабая связь между колебательным контуром и генератором. Для измерения напряжения на конденсаторе используют электронный вольтметр V. Второе реактивное сопротивление z2 служит для развязки контура от цепи этого вольтметра. В колебательный контур входят: исследуемый образец с обмоткой, обладающей индуктивностью Lx и сопротивлением Rx, переменная емкость Cv для настройки контура в резонанс и собственная емкость Ср катушки и соеди-
325

нительных проводов. Определение действительной и мнимой частей комплексной магнитной проницаемости основывается на связи этих величин с индуктивностью Lx и сопротивлением Rx. Расчетные формулы имеют вид
|
|
|
Lx l |
, |
(6.52) |
|
1 |
n2 S |
|||||
|
|
|
|
|||
|
|
|
|
|
2 Rx l , (6.53) n2 S
где - угловая частота переменного поля, n - число витков обмотки, S - сечение образца, l - длина образца по средней линии.
Таким образом, измерив величины Lx и Rx, можно по формулам (6.52), (6.53) найти значение величин 1 и 2. Индуктивность
Lx определяют по резонансной емкости C в тот момент, когда
v
напряжение на колебательном контуре будет максимальным. Для этого применяется формула
Lx |
|
|
1 |
|
|
|
|
. |
(6.54) |
|
|
|
|
|
|
|
|||||
2 |
C |
C |
p |
|
||||||
|
|
|
|
|||||||
|
|
|
v |
|
|
|
|
|
||
Тангенс угла потерь рассчитывается так:
tg |
Cv |
|
|
, |
(6.55) |
2 C C |
|
|
|||
|
v |
p |
|
|
|
где CV называется резонансной шириной. Эта величина определяется при двух значениях Cv, для которых общее сопро-
тивление настроенной цепи в 1

 2 раз меньше максимальной
2 раз меньше максимальной
величины.
При осуществлении этого метода следует иметь в виду источники ошибок, которые зависят от следующих факторов. Прежде всего следует измерить или рассчитать собственную емкость Ср. В противном случае возникнет значительная ошибка в
326
измеряемой величине индуктивности Lх. Наличие собственной емкости Ср позволяет применять рассматриваемый метод только для определенных значений частот. Кроме того, этот метод может быть применен для исследования материалов с небольшими потерями, чтобы резонансная кривая не была плоской. Следует также иметь в виду, что на результаты измерения влияет собственная самоиндукция катушки и соединительных проводов.
6.6. Магнитооптические методы исследования ферромагнетиков
Каждая из представленных выше методик обладает не только определенным преимуществом, но и конкретными недостатками, которые не дают сведений об электронной структуре исследуемых магнитоупорядоченных материалов. Указанными недостатками не страдают магнитооптические методы (МО). Более того, МО методы будто бы "придуманы" для исследований физических свойств таких материалов.
Современная магнитооптика - раздел физики, сформированный на стыке двух наук: физической оптики и физики магнитных явлений, изучающий взаимодействие света с намагниченным или магнитоупорядоченным веществом. В результате спектральных, полевых и температурных зависимостей МО исследований решаются фундаментальные задачи, касающиеся связи магнитоупорядо-ченного твердого тела с оптическими явлениями, и конкретнее, определения природы и механизмов поглощения света магнитоконцентрированными кристаллами, анизотропии оптических свойств кристалла, помещенного во внешнее магнитное поле; восстанавливаются спектры электронных энергетических состояний в ферромагнетиках, связывающие энергию квазичастиц с их импульсом; выявляются виды магнитных взаимодействий и типы магнитных структур, а также магнитных фазовых превращений "поверхностного" магнетизма и т.д.
327
Решение этих вопросов, а также многих неназванных, важны не только в чисто научном плане. В них заключена также научная основа для практических приложений и, в первую очередь, для конструирования материалов с заданными магнитными и МО параметрами, для разнообразных применений материалов в современных элементах магнитной памяти и интегральной оптики, в качестве управляющих элементов оптических трактов и магнитооптических устройств, в лазерной технике и т.п.
Оптические и МО методы являются наиболее простыми, эффективными и информативными. МО методы обладают рядом достоинств, главное из которых состоит в том, что в отличие от оптических они чувствительны к знаку спина, что позволяет выделить: к какой спиновой зоне относится данный оптический переход. Большие возможности магнитооптической спектроскопии связаны с тем, что наиболее важные межзонные интервалы, интервалы между отдельными уровнями и их компонентами, энергии обменного и спин-орбитального расщепления энергетических зон ферромагнетика попадают в оптическую область спектра. МО методам присуща уникальная особенность - это, в принципе, динамические методики, которые несут отклик электронной системы на модуляцию вектора спонтанной намагниченности, что обеспечивает высокую чувствительность, характерную для всех дифференциальных методик. Эти методы, несмотря на долгую жизнь, продолжают совершенствоваться как в методическом отношении, так и в чисто научном плане. В подавляющем большинстве случаев, однако, целенаправленно проводимые эксперименты в идейном отношении не являются принципиально новыми, но их широкое использование в исследованиях, а также быстрый рост числа соответствующих публикаций свидетельствует о том, что МО методы и основанные на их принципах устройства, установки и приборы стали неотъемлемыми рабочими инструментами физики твердого тела.
328
6.6.1. Электромагнитные волны в среде
Рассмотрение магнитооптических явлений в веществе начнем с необходимых напоминаний, касающихся природы и свойств электромагнитного излучения оптического диапазона длин волн. Этот диапазон с условными границами от частот3 1012 Гц до 3 1018 Гц включает три более коротких интервала: инфракрасное излучение в диапазоне длин волн
103 0,76 мкм, |
видимое |
излучение |
(собственно |
свет) |
0,76 0,4 мкм, |
или 1012 |
1016 Гц, ( h 1,5 3 эВ), |
ульт- |
|
рафиолетовое излучение 0,4 0,1мкм. |
|
|
||
В дальнейшем нас будут интересовать главным образом световые электромагнитные волны, и поэтому характеристики интервалов их "существования" представлены и в длинах волн, и в частотах, и в энергиях. Взятое в кавычки слово существование следует понимать не только в смысле указания их интервалов, но и в том, что электромагнитные волны существуют как самоподдерживающийся процесс возникновения и распространения в пространстве быстропеременных электрического и магнитного полей, являющихся функцией частоты:
|
|
|
r |
|
r |
t ) |
|
|
|
|
E( r ,t ) E e( kr |
|
|||
|
|
|
r r |
r |
0 |
|
(6.56) |
|
|
|
rr |
|
|||
|
|
|
t ) |
|
|||
|
|
|
B( r ,t ) B e( kr |
|
|||
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
Здесь k |
c n |
– волновой вектор, определяющий распростра- |
|||||
нение волны, |
|
– вектор рефракции, 2 , с — скорость |
|||||
n |
|||||||
света в вакууме. |
|
|
|
|
|||
|
|
|
|
|
|
||
О частотной зависимости векторов E и B световой |
|||||||
волны говорят, |
как о цвете; квадраты E 2 и B 2 |
дают энергию |
|||||
329
волны; интенсивность волны определяется средним по време- |
||||
|
|
|
|
|
ни значением плотности потока энергии ~ E |
B . |
|
||
|
|
|
t |
|
Система |
уравнений |
электромагнитного |
поля, |
|
источниками которого являются заряды объемной плотности |
||||||
|
|
|
|
|
|
|
и тока проводимости плотности j |
|
|
||||
|
|
|
|
|
|
|
divE |
|
, |
|
|
||
|
|
|
(6.57,а) |
|||
|
|
0 |
|
|||
|
|
|
|
|||
|
|
|
B , |
|
|
|
rotE |
|
(6.57,b) |
||||
|
|
|
t |
|
||
|
|
|
|
|
||
|
0 , |
|
(6.57,c) |
|||
divB |
|
|||||
|
j |
|
E , |
|
|
|
c2 rotB |
|
|
|
|||
|
|
|
(6.57,d) |
|||
|
0 |
|
t |
|
||
|
|
|
|
|||
дополненная материальными уравнениями , учитывающими |
||||||
|
|
|
|
|
|
|
соотношения между векторами E, D, B, H и |
j |
|||||
D |
E |
|
|
|||
r |
|
|
|
r |
|
|
B H |
|
(6.58) |
||||
r |
|
|
r |
|
|
|
j |
E |
|
|
|||
и граничными условиями,— это система уравнений Максвелла
для материальных сред. D – вектор электрического смещения, среды, – электропроводность.
330
