Экспериментальные методы исследований. Калинин Ю.Е

осциллографа (3), для чего на штоке располагается катушка (14), находящаяся между неподвижными постоянными магнитами (2) и (13). С помощью электромагнита (5) создается внешнее магнитное поле, которое намагничивает образец (4).

Принцип работы магнитометра основан на возникновении ЭДС в неподвижных катушках при колебании магнитного образца в подмагничивающем магнитном поле. Ферромагнитный образец (4) размером 53 мм2 закрепляется на штоке (10), жестко связанным с эластичной пластиной электромагнита (1), предназначенного для возбуждения механических колебаний образца в магнитном поле электромагнита (5). ЭДС, возникающая в катушках, пропорциональна намагниченности образца. В выносном усилителе (8) сигнал с катушек предварительно усиливается в 10 раз и подается на канал ”a” усилителя-преобразователя УПИ-2.

Опорный сигнал на канал ”b” УПИ-2 подается от генератора (6) с той же частотой, с которой совершает колебания шток. Вид усиливаемого сигнала контролируется на канале 2 осциллографа (3). Сигнал, пропорциональный намагниченности образца, снимается с канала ”d” УПИ-2 и подается на канал ”Y” самописца (12) (АЦП). Напряжение с датчика Холла (11), пропорциональное напряженности магнитного поля, подается на канал “Х” самописца (12) (АЦП). Для определения абсолютных значений намагниченности исследуемых образцов магнитометр предварительно калибруется. Для этого проводится измерение сигнала от эталонного материала с известной намагниченностью. В качестве эталонного образца обычно используется фольга Ni, намагниченность насыщения которой равна 0,61 Тл. Относительно этого значения осуществляется пересчет намагниченности исследуемых материалов. Намагниченность исследуемого образца вычисляется по следующей формуле:

311

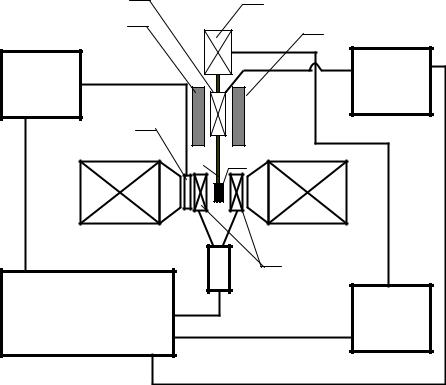
Рис. 6.7. Структурная схема вибрационного магнитометра: 1 – электромагнит с эластичной пластиной; 2,13 – постоянные магниты; 3 – осциллограф; 4 – образец; 5 – намагничивающий

электромагнит; 6 – генератор сигналов специальной формы Г6-26; 7 – катушки; 8 – усилитель выносной; 9 – усилительпреобразователь УПИ-2; 10 – шток; 11 – датчик Холла; 12 – самописец; 14 – катушка

где IХ – искомая намагниченность, Ni – удельная намагниченность Ni, VNi – объем Ni, VX – объем исследуемой пленки, Ni –

312

значение максимального сигнала от Ni, Х – значение максимального сигнала исследуемой пленки, ρNi – плотность Ni .

Вибрационный магнитометр позволяет производить исследование магнитных свойств в зависимости от напряженности магнитного поля и температуры. Для проведения измерений при различных температурах исследуемый образец помещают в нагревательную печь или в криогенное устройство.

6.5.2. Методы измерения в переменных магнитных полях

Магнитные характеристики ферромагнитных веществ в переменных полях зависят не только от физических свойств материала, но и от формы и размеров образцов, частоты и вида кривой H(t) переменного поля. Если глубина проникновения магнитного поля меньше толщины образца, то говорят о действующих или средних значениях индукции и проницаемости. Поэтому, когда определяют магнитные характеристики в переменном магнитном поле, фиксируют условия, при которых они были определены. Большинство используемых в настоящее время схем основано на индукционном методе измерения характеристик в переменных полях. С помощью этих схем, как правило, определяют электрические величины, по значениям которых рассчитывают магнитные характеристики.

Напряженность магнитного поля находят по действующему значению тока в намагничивающей обмотке

H дейст niR , (6.24)

где n - число витков намагничивающей обмотки, R — радиус кольца (м), i — действующее значение тока (A).

Для расчета амплитудной магнитной проницаемости используют формулу

313

где Вт – максимальная магнитная индукция.

Иногда для вычисления амплитудной магнитной проницаемости определяют индуктивность образца

где U и i — действующие значения напряжения и силы тока,- круговая частота.

Магнитную проницаемость рассчитывают по соотношению

где l - длина образца (м), S - сечение образца (м2), n - число витков намагничивающей обмотки.

Кривую индукции в переменных полях можно определять методом амперметра и вольтметра, потенциометрическими и мостовыми методами.

6.5.2.1. Метод вольтметра и амперметра

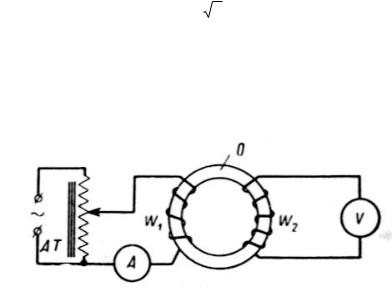
Магнитные характеристики в переменных полях промышленной частоты можно определить с помощью простейшего метода вольтметра и амперметра. Образец при этом методе используют в форме тороида или рамки, которую собирают из тонких пластин исследуемого вещества. На иссле-дуемый образец О наматывают измерительную обмотку W2 и намагничивающую обмотку W1. Ток в цепи обмотки W1 можно измерять при помощи амперметра, а э.д.с. в обмотке W2 измеряют цифровым вольтметром (рис. 6.8).

Для регулировки тока в намагничивающей обмотке рекомендуют использовать лабораторный автотрансформатор, который не искажает синусоидальной формы кривой тока i(t). Расчет магнитной индукции образца производят по формуле

314

где Еср – среднее значение ЭДС во вторичной обмотке, w2 – число витков вторичной обмотки, f – частота тока, S – сечение образца.

Максимальное значение напряженности намагничивающего поля в замкнутой цепи определяется по формуле

где i - действующее значение намагничивающего тока, w1 - число витков намагничивающей обмотки, l - средняя длина магнитной цепи.

Рис. 6.8. Схема измерения кривой индукции методом амперметра и вольтметра:

О– исследуемый образец; W1 – намагничивающая обмотка; W2 – измерительная обмотка; АТ - автотрансформатор

Пропуская через намагничивающую цепь определенные значения тока и измеряя при помощи вольтметра э.д.с. во вторичной обмотке, можно по формулам (6.48) и (6.49) рассчитать магнитную индукцию и напряженность магнитного поля, по-

315

строив зависимость В – (Н). Амплитудные значения проницаемости определяют по формуле (6.47).

Метод вольтметра и амперметра не дает возможности определять потери в образце и обладает большой погрешностью измерения индукции порядка 10 – 15 %. Несмотря на отмеченные недостатки, этот метод находит широкое распространение для определения кривой индукции магнитомягких веществ, так как он отличается простотой и может быть создан в любых лабораторных условиях.

6.5.2.2. Мостовые методы измерения магнитных характеристик

Мостовые методы определения магнитных характеристик в переменных магнитных полях в большинстве случаев используют для исследования магнитомягких материалов. Мостовые методы измерения получили большое распространение в лабораторной практике по той причине, что они могут быть быстро созданы и не требуют сложной физической аппаратуры.

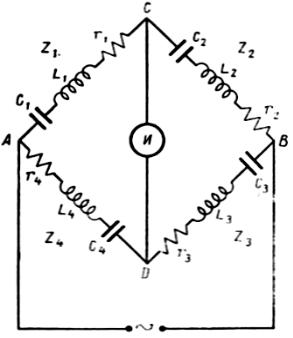
Рассмотрим принципиальную схему моста, которая показана на рис. 6.9. В плечи моста переменного тока включают активное rп и реактивные сопротивления Сп и Ln, где n = 1, 2, 3, 4, а в диагонали моста имеется прибор И переменного тока, который выполняет роль индикатора. Когда мост находится в равновесии, то в диагонали моста CD тока нет. В этот момент потенциалы в точках С и D равны между собой и падение напряжения на участках моста одинаковое. Обозначим

316

где z1, z2, z3 и z4 – полные сопротивления плеч моста в комплексной форме.

Из последних равенств при равновесии моста имеем

Поскольку полное сопротивление каждого плеча в отдельности в комплексной форме записывается в виде

то, согласно (6.31) после соответствующих преобразований из соотношения получаем

r1r3 r2 r4 j(x1r3 r1 x3 ) x1 x3 x2 x4 j x2 r4 r2 x4 . (6.33)

Чтобы выполнялось последнее равенство, вещественные и мнимые части должны быть порознь равны друг другу, т. е.

r1r3 r2 r4 x1 x3 x2 x4 ,

Уравнения (6.34) показывают, при каких условиях мост находится в равновесии. На практике для удобства применяют такие мостовые схемы, у которых условия равновесия имеют более простой вид, а именно

r1r3 r2 r4 0,

Таким образом, как видно из соотношений (6.35), для получения равновесия моста переменного тока достаточно

317

уравновесить в отдельности активные и реактивные составляющие сопротивлений плеч моста.

Мост с переменной индуктивностью

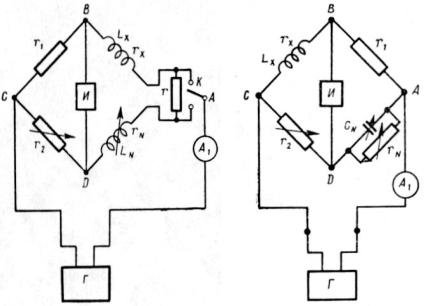
Принципиальная схема моста, в одном плече которого имеется переменная индуктивность, показана на рис. 6.10. Мост переменной индуктивности состоит из четырех плеч: два плеча обладают только активными сопротивлениями r1 и r2, при этом сопротивление r2 является переменным. Третье плечо AD имеет переменную индуктивность Lx, активное

Рис. 6.9. Принципиальная схема моста переменного тока

сопротивление которого обозначается через rx. В плече АВ имеется исследуемый образец с обмоткой. Мост подключают к генератору Г. В процессе измерения определяют значения индуктивности Lx и активного сопротивления rх. По этим вели-

318

чинам рассчитывают магнитные характеристики вещества. Переменные сопротивления r включают между плечами AD и АВ, которые имеют также реактивные сопротивления. Из рис. 6.10 видно, что сопротивление r может быть включено при помощи ключа K в любое из этих плеч. Запишем сопротивление плеч моста в комплексной форме:

плеча АВ zx r rx j Lx ,

них равенств. Для этого нужно приравнять действительные и мнимые части. Тогда окончательно получим

r

rx rN r1 r,

2

Lx LN rr1 . (6.39)

2

Для более точного определения величин Lx и rx измерения следует производить при нескольких значениях напряжений, подаваемых на мост. Амплитудную проницаемость образца рассчитывают по формуле

319

где dcp - средний диаметр тороида. Для того чтобы определить магнитную индукцию исследуемого образца и напряженность магнитного поля, нужно найти значение тока в намагничивающей обмотке образца. Полный ток в этой обмотке в комплексной форме записывается в виде

Подставив в эту формулу значения rх и Lx, согласно формуле (6.36) получим выражение для модуля тока

320