Учебники 80251

Рассмотрим построение диаграммы Боде (логарифмическая амплитудночастотная характеристика — ЛАЧХ). Как известно, она определяется как:

Полученная диаграмма Боде (ЛАЧХ) для RLC –цепи представлена на рис. 16:

Рис. 16. Диаграмма Боде (ЛАЧХ) для RLC –цепи

График в логарифмическом масштабе построен с помощью функции plot2d1. Первый аргумент этой функции – строка из трех символов, которая определяет вид графика. Первый символ о означает, что в случае построения нескольких кривых на одном графике аргумент x для них будет один и тот же. Следующие два символа определяют способ масштабирования осей x и y (соответственно): l – означает логарифмический масштаб, n – линейный.

Частотные характеристики системы можно также получить и с помощью функции syslin. Рассмотрим ее применение на примере дифференцирующего звена с замедлением, передаточная фунция которого имеет вид:

21

где K, T – параметры , .

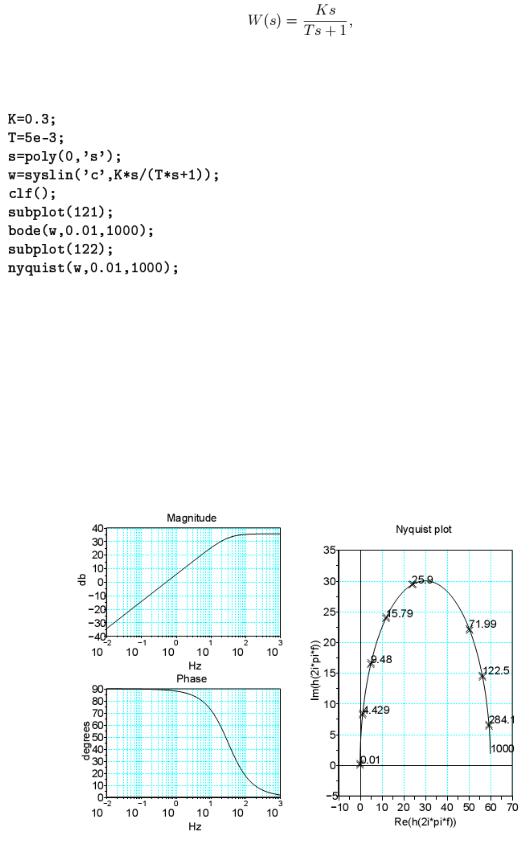
Построим диаграмму Боде и годограф Найквиста такой системы при Т=0,3, К=5*10-3.

Первый параметр функции syslin определяет тип системы: непрерывная(«c») или дискретная («d»). Вторым параметром задаем передаточную функцию данного звена. Для этого вначале введена переменная s в качестве аргумента многочлена. С помощью функции bode построена диаграмма Боде (ЛАХ и ЛФЧХ), а с помощью функции nyquist – кривая Найквиста (АФХ). Эти функции имеют одинаковые наборы входных параметров: первым параметром передается имя системы, созданной при помощи оператора syslin, а вторым и третьим аргументами – минимальная и максимальная частоты соответственно (рис. 17).

Рис. 17. Диаграмма Боде и годограф Найквиста

22

Лабораторная работа № 8 ПРИМЕРЫ ИССЛЕДОВАНИЯ ДИНАМИЧЕСКИХ СИСТЕМ

1. ЦЕЛЬ РАБОТЫ

Научиться рассчитывать переходные процессы с помощью Scilab.

2. ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Упражнение 1. Расчет переходных процессов.

Задачи моделирования часто сводятся к интегрированию систем обыкновенных дифференциальных уравнений (ОДУ) первого порядка вида

(рис. 18):

Для решения ОДУ используется функция Scilab ode.

В качестве первого примера рассмотрим RLC-цепочку, входом будем считать падение напряжения на всей цепи, а выходом – заряд конденсатора q(t). Из второго закона Кирхгофа следует:

откуда получим систему линейных дифференциальных уравнений первого порядка:

Проинтегрируем ее при помощи функции ode. Для интегрирования следует написать головную программу, содержащую обращение к процедуре ode и подпрограмму-функцию, в которой вычисляются правые части системы дифференциальных уравнений. В головной программе должны быть заданы начальные условия для всех переменных, начальное и конечное значения аргумента интегрирования.

23

Вместо того, чтобы описывать подпрограмму-функцию в отдельном файле, можно описать ее непосредственно в головной программе с помощью функции deff, как это сделано в приведенном примере. Первым параметром этой функции является строка вида:

[s1,s2,...]=newfunction(e1,e2,....), где s1, s2, ...–выходные переменные, e1,e2,... – входные переменные, а =newfunction – имя описываемой функции. Второй аргумент – строка, определяющая последовательность инструкций создаваемой функции.Таким образом, команда: deff(’dy=F(t,y)’,’dy=Q*y+P*u(t)’); определяет функцию, аналогичную функции, описываемой в отдельном файле:

functiondy=F(t,y)

dy=Q*y+P*u(t); endfunction

Втаком случае переменные Q и P необходимо определить как глобальные или определять в самой подпрограмме.

Врассмотренной программе были описаны две функции: первая вычисляет правые части системы дифференциальных уравнений, а вторая задает синусоидальное входное воздействие. Входными параметрами функции

ode являются y0 – вектор начальных состояний, t0 – начальный момент времени, T – моменты времени, для которых производится вычисления, F – подпрограмма-функция, вычисляющая правые части системы дифференциальных уравнений.

Выходным аргументом в данном примере будет вектор: Y=(I,q) (рис. 18).

Рис. 18. Моделирование RLC – цепочки

24

Часто в подпрограмму нужно передавать дополнительные аргументы. Так, для функции dy=f(t,y,u1,...,un) требуются дополнительные параметры u1,...,un. Эти аргументы можно передать при вызове функции ode как список вида list(f,u1,...un).

Рассмотрим нелинейную систему (рис. 19):

Напишем следующую подпрограмму вычисления правых частей второй системы:

Текст головной программы:

Рис. 19. Фазовая траектория системы (2) на плоскости (y1, y2)

25

Лабораторная работа № 9 МОДЕЛИРОВАНИЕ В SCICOS

1.ЦЕЛЬ РАБОТЫ

1.Изучить программирование на наглядных примерах в редакторе Scicos

2.Получить опыт моделирования в редакторе Scicos для создания собственных моделей.

.

2.ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ

Пример 1

Рассмотрим структуру системы оценивания в пространстве состояний, получающую выборку данных от линейной системы. Система смоделирована как линейная непрерывная:

x = Ах + Вu,

у = Cx, где A, B, C - постоянные матрицы.

Наблюдению доступен вектор y, поступающий на вход без шумов. Кроме того, на вход поступает управление u и начальное значение вектора х: х0. На выходе формируется оценка x€. Переходный процесс в такой системе должен быть по возможности коротким, но при этом флуктуационная составляющая ошибки не должна быть велика.

Уравнение оценивания в таком случае имеет вид:

x = A x€ + Bu + K(y−C x€).

Матрица K должна быть выбрана так, чтобы у собственных значений − KC были отрицательные вещественные части.

Текст программы Scilab для выполнения этой процедуры с неопределенными заранее матрицами, помещенными в контекст модели, является следующим:

Функция ppol используется, чтобы получить матрицу усиления K. На вход u подается sin (t) (рис. 20).

26

Рис. 20. Функция ppol

Использование символических параметров полезно, потому что оно позволяет нам создавать универсальную модель. Чтобы изменить матрицы A, B, и C и размерность системы или время дискретизации, мы должны изменить только определение m, n и матрицы. Никаких изменений в схеме не требуется

(рис. 21).

Рис. 21. Изменение символических параметров

На левой панели показаны параметры до их изменения. На правой – после изменения.

Фактически, перезаписывая контекст, мы можем сделать диаграмму полностью универсальной.

Сделаем загрузку:

27

Мы только должны удостовериться, что файл данных datafile содержит переменные A, B, C, D, x0, и dt прежде, чем начать сеанс Scicos. Этот файл может быть создан в Scilab следующим образом:

→save('datafile'',A,B,C,x0,dt)

Если контекст содержит много строк кода Scilab, удобно поместить код в отдельный файл скрипта и выполнить его единственной командой exec в контексте. Однако, если файл, выполняемый командой exec, изменен, когда модель уже открыта и пользователь хочет, чтобы изменения были приняты во внимание, он должен сделать оценку, потому что у Scicos нет никакого способа узнать, были ли сделаны изменения.

Нужно также отметить, что использование отдельного файла скрипта подразумевает, что диаграмма Scicos не является модульной, и этот файл скрипта должен всегда сопровождать модель.

Пример 2

Решить дифференциальное уравнение y'"' + y'"+ y" + 0.5y' + 0.1y = 0.1,

при нулевых начальных условиях.

Для самой высокой производной запишем y'"' = - y'"- y" - 0.5y´- 0.1y + 0.1.

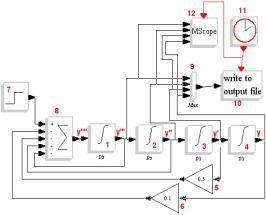
Предположим, что y'"' известна. Тогда, после четырехкратного интегрирования получим у. Самая высокая производная, y'"' существует между блоками 8 и 1 (рис. 22).

Рис. 22. Максимальное значение производной у

Постоянное слагаемое 0.1 формируется блоком 7 как шаг в момент t=0. Производные y'", y", y' и y отoбражаются в MScope 12.

Результаты решения через мультиплексор 9 записаны в файл в ASCIIкоде блоком 10.

Начальные условия у всех интеграторов нулевые, в соответствии с условиями задачи.

28

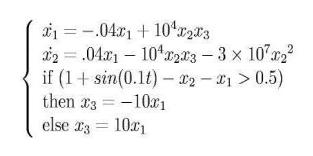
У интеграторов есть верхние и нижние пределы. Необходимо не забывать задать их перед пуском.

Блок 7 по умолчанию имеет начальное время ступени равное 1. Его необходимо заменить на 0.

Блоки 5 и 6 не обязательны, так как можно установить входной множитель в блоке 8. Здесь они включены для наглядности.

Часы активации имеют начальное время равное нулю, а период 0.1. Это не имеет никакого отношения к точности решения, а только задает шаг выхода.

MScope имеет размерность входных портов портов {1 1 1 1}. Величины Ymin и Ymax были установлены после первого прогона. Период обновления (refresh-period) такой же как окончательное время интегрирования.

Запись в файл (блок 10) удобна тем, что данные могут быть импортированы в другие программы. Необходимо задать имя файла и задать строку формата в стиле Fortran. Это значит:

формат пишется в круглых скобках и включает: / – новая линия;

iw – область целого числа с шириной w знаков;

fw.d – область числа с плавающей запятой шириной w знаков, включая d цифры после десятичной запятой. Здесь w> = d+3, чтобы включить по крайней мере одну цифру целого числа, знак и точку;

ew.d – область числа с плавающей запятой, степень десяти шириной w знаков, включая d цифры после десятичной запятой. Здесь w> = d+7, чтобы включить по крайней мере одну цифру целого числа, знак для мантиссы, трех знаков для экспоненты, знака экспоненты и одного для точки;

nx n – пробелы;

tn – перемещает курсор принтера в положение n.

В этом примере выбрано (7 (e16.8,1x)) для строки формата (8 десятичных чисел), так как величины переменных малы.

Пример 3

Рассмотрим решение еще одного ДУ.

Продемонстрируем простым примером, как моделирование некоторых уравнений может стать сложным (можно показать как эту задачу можно облегчить с помощью компонентов Modelica). Рассмотрим систему ДУ:

Теперь покажем реализацию этих уравнений в модели (рис. 23).

29

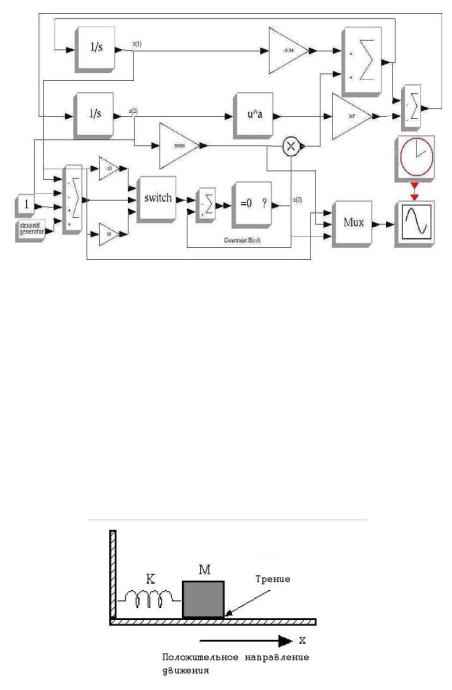
Рис. 23. Реализация уравнений в модели

В блочном подходе есть несколько недостатков. Для моделирования часто необходимо слишком много блоков. Это делает модель неудобочитаемой. Также в такой сложной блок-схеме трудно отразить наглядно структуру физической или технической задачи.

Пример 4

Блок с массой М перемещается по грубой поверхности с коэффициентом трения f. Постоянная сила сопротивления – f·M·g, где g – сила тяготения, и K – коэффициент упругости пружины.

Покажем движение блока на графике (рис. 24), если его перемещают на 1 метр направо и отпускают.

Рис. 24. Движение блока

Такое движение можно описать уравнением: y" = -y - 0.15*sign (y').

Начальное условие для положения установлено в 1 метр (в блоке интегратора 2), время окончания интеграции 9.4, время обновления MScope 10. Период часов активации 0.01, а начальное время равно нулю (рис. 25-27).

30