Учебники 80153

лу на каждом элементарном отрезке, получим составную квад-

ратурную формулу Симпсона:

Если проводить параболы через точки с абсциссами xi 1, xi 1 h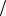2, xi и соответствующими ординатами yi 1, yi 12 , yi , то формула Симпсона примет вид:

Отметим, что формула Симпсона имеет четвертый порядок точности.

В курсе «Теория вероятностей и математическая статистика» дифференцирование широко используется для нахождения плотности распределения вероятностей при известной функции распределения вероятностей случайной величины

нахождения функции распределения вероятностей случайной

роятности попадания случайной величины в определенный ин-

x2

тервал P x1 X x2 F x2 F x1 pX x dx или в оп-

x1

ределенную область P (X, Y) D pXY (x, y)dxdy , для оп-

D

ределения плотности распределения вероятностей отдельных компонент случайного вектора:

Задание к выполнению лабораторной работы.

1)Найти аналитические выражения для первой и второй производной функции f (x) своего варианта (табл. 1).

2)Вычислить точные и приближенные значения первой и второй производной функции f (x) в середине отрезка локали-

чение f (x)dx, приближенное значение f (x)dx, точные

и define, определяем функцию f 2(x) как производную f (x)

спомощью встроенных функций diff и define.

2)Вычисляем точные значения первой и второй производной функции f (x) в середине отрезка локализации корня.

Определяем шаг h как длину отрезка локализации, деленную на 10. Создаем выражение f1p(x) для вычисления приближенного значения первой производной согласно формуле (3.3) и вычисляем приближенное значение первой производной функции f (x) в середине отрезка локализации корня. Создаем выражение f 2p(x) для вычисления приближенного значения первой производной согласно формуле (3.4) и вычисляем при-

встроенной функции integrate( f (x),x,a,b) . Приближенное зна-

b

чение f (x)dx находим с помощью встроенной функции

a

romberg( f (x),x,a,b) из пакета romberg .

5) Создаем функцию f (x, y). Находим аналитическое

выражение f (x, y)dxdy dx f (x, y)dy с помощью встро-

енной функции integrate(integrate( f (x),y),x) . Точное значение

b y2(x)

интеграла dx f (x, y)dy находим с помощью встроенной

a y1(x)

функции integrate(integrate( f (x), y, y1(x), y2(x)),x,a,b), а при-

ближенное значение находим с помощью встроенной функции romberg(romberg( f (x), y, y1(x),y2(x)),x,a,b).

Пример выполнения лабораторной работы

1) (%i) f(x):=log(cos(x^2+1)); (%i) define(f1(x),diff(f(x),x));

(%i) define(f2(x),diff(f(x),x,2));

2)(%i) f1(0.25); -0.897466078632706 (%i) f2(0.25); -4.645309676827188 (%i) h:0.05;

(%i) f1p(x):=(f(x+h)-f(x-h))/(2*h); (%i) f1p(0.25);

-0.903569482862924

(%i) f2p(x):=(f(x-h)-2*f(x)+f(x+h))/(h^2); (%i) f2p(0.25);

-4.66663672974179

3)(%i) g(x,y):=atan(x/(25*y));

(%i) g1x(x,y):=diff(g(x,y),x,1); (%i) g1x(x,y);

(%i) g1y(x,y):=diff(g(x,y),y,1); (%i) g1y(x,y);

(%i) g2x:diff(g(x,y),x,2);

(%i) g2y:diff(g(x,y),y,2);

(%i) g2xy:diff(g1x(x,y),y);

4) (%i) f(x):=25*x*exp(-25*x^2); (%i) integrate(f(x),x);

(%i) integrate(f(x),x,0,1/25);

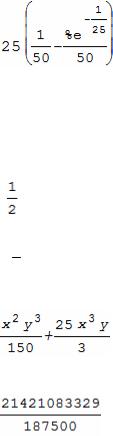
(%i) float(%); 0.0196052804238384 (%i) load(romberg);

(%i) romberg(f(x),x,0,1/25); 0.0196053203562632

(%i) integrate(f(x),x,0,inf);

(%i) integrate(f(x),x,minf,0);

1

2

5) (%i) f(x,y):=25*x^2+x*y^2/25; (%i) integrate(integrate(f(x,y),y),x);

(%i) integrate(integrate(f(x,y),y,0,x/25), x,1,1+25);

(%i) float(%); 114245.7777546667

(%i) romberg(romberg(f(x,y),y,0,x/25),x, 1,1+25);

114245.7820949445

Контрольные вопросы

1. В каких случаях применяется численное дифференцирование?

2.Запишите простейшие формулы для вычисления производных первого и второго порядка.

3.Дайте геометрическую интерпретацию формул для производной первого порядка.

4.Каков порядок точности этих формул?

5.Почему приближенное дифференцирование является некорректной операцией?

6.Как реализуется вычисление производных с помощью стандартных средств пакета Maxima?

7.В каких случаях применяется численное интегрирова-

ние?

8.Как разбивается площадь исходной криволинейной трапеции на сумму площадей элементарных криволинейных трапеций?

9.Как вычисляется площадь элементарной криволинейной трапеции в методе левых прямоугольников?

10.Как вычисляется площадь элементарной криволинейной трапеции в методе правых прямоугольников?

11.Как вычисляется площадь элементарной криволинейной трапеции в методе центральных прямоугольников?

12.Как вычисляется площадь элементарной криволинейной трапеции в методе трапеций?

13.Как вычисляется площадь элементарной криволинейной трапеции в методе Симпсона?

14.Какой порядок точности имеют методы прямоугольников, трапеций, Симпсона?

15.Как реализуется точное вычисление интегралов с помощью стандартных средств пакета Maxima?

16.Как реализуется точное вычисление интегралов с помощью стандартных средств пакета Maxima?

17.В каких случаях используется дифференцирование в курсе «Теория вероятностей и математическая статистика»?

18.В каких случаях используется интегрирование в курсе «Теория вероятностей и математическая статистика»?

Форма отчетности: Отчет должен содержать название лабораторной работы, задание для конкретного варианта, все командные строки, результаты расчетов аналитические и численные (в десятичных дробях три цифры после запятой).

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1.Плис А.И. Лабораторный практикум по высшей математике / А.И. Плис, Н.А. Сливина. М.: Высш. шк., 1994.

2.Амосов А.А. Вычислительные методы для инженеров / А.А. Амосов, Ю.А. Дубинский, Н.В. Копченова. М.: Высш.

шк., 1994.

3.Бабенко К.И. Основы численного анализа / К.И. Бабен-

ко. М.: Наука, 1986.

4.Бахвалов Н.С. Численные методы / Н.С. Бахвалов, Н.П. Жидков, Г.М. Кобельков. М.: Наука, 1987.

5.Боглаев Ю.П. Вычислительная математика и программирование / Ю.П. Боглаев. М.: Высш. шк., 1990.

6.Волков Е.А. Численные методы / Е.А. Волков. М.:

Наука, 1987.

7.Демидович Б.П. Основы вычислительной математики / Б.П. Демидович, И.А. Марон. М.: Наука, 1966.

8.Иванов В.В. Методы вычислений на ЭВМ / В.В. Иванов. Киев: Наукова думка, 1986.

9.Калиткин Н.Н. Численные методы / Н.Н. Калиткин. М.:

Наука, 1978.

10.Марчук Г.И. Методы вычислительной математики / Г.И. Марчук. М.: Наука, 1989.

11.Самарский А.А. Численные методы / А.А. Самарский, А.В. Гулин. М.: Наука, 1989.

12.Турчак Л.И. Основы численных методов / Л.И. Турчак. М.: Наука, 1987.

13.Воробьева Г.Н. Практикум по вычислительной математике / Г.Н. Воробьева, А.Н. Данилова. М.: Высш. шк., 1990.

14.Гмурман В.Е. Теория вероятностей и математическая статистика / В.Е. Гмурман. М.: Высш. шк., 1998.

15.Вентцель Е.С. Теория вероятностей / Е.С. Вентцель.

М.: Наука, 1999.

16.Кремер Н.Ш. Теория вероятностей и математическая статистика / Н.Ш. Кремер. М.: ЮНИТИ-ДАНА, 2004.

17.Кибзун А.И. Теория вероятностей и математическая статистика. Базовый курс с примерами и задачами / А.И. Кибзун, Е.Р. Горяинова, А.В. Наумов. М.: Физматлит, 2002.

18.Андронов А.М. Теория вероятностей и математическая статистика / А.М. Андронов, Е.А. Копытов, Л.Я. Гринглаз. СПб.: Питер, 2004.

19.Письменный Д.Т. Конспект лекций по теории вероятностей и математической статистике / Д.Т. Письменный. М.: Айрис-пресс, 2004.

20.Дубровская А.П. Теория вероятностей и элементы математической статистики / А.П. Дубровская, В.И. Минаков. Воронеж: ВПИ, 1993.

21.Глушко Е.Г. Элементы теории вероятностей и математической статистики / Е.Г. Глушко, А.П. Дубровская. Воронеж: ВГТУ, 2004.

22.Колемаев В.А. Теория вероятностей и математическая статистика / В.А. Колемаев, О.В. Староверов, В.Б. Турундаевский. М.: Высш. шк., 1991.

23.Чистяков В.П. Курс теории вероятностей / В.П. Чистяков. М.: Наука, 1987.

24.Гурский Е.И. Теория вероятностей с элементами математической статистики / Е.И. Гурский. М.: Наука, 1971.

25.Захаров В.К. Теория вероятностей / В.К. Захаров, Б.А. Севостьянов, В.П. Чистяков. М.: Наука, 1983.

26.Гнеденко Б.В. Курс теории вероятностей / Б.В. Гнеденко. М.: Наука, 1988.

27.Прохоров Ю.В. Теория вероятностей / Ю.В. Прохоров, Ю.А. Розанов. М.: Наука, 1973.

28.Боровков А.А. Курс теории вероятностей / А.А. Боровков. М.: Наука, 1976.

29.Пугачев В.С. Теория вероятностей и математическая статистика / В.С. Пугачев. М.: Наука, 1979.

30.Ивашев-Мусатов О.С. Теория вероятностей и математическая статистика / О.С. Ивашев-Мусатов. М.: Наука, 1979.

31.Дежин В.В. Использование математического моделирования при решении экономических вероятностных задач: методические указания для организации самостоятельной работы по курсу «Теория вероятностей и математическая статистика» студентов направления 080100 «Экономика» профиля «Экономика предприятий и организаций» очной формы обучения. Ч. 1 / В.В. Дежин. Воронеж: ВГТУ, 2013. (№ 150-2013)

32.Дежин В.В. Использование математического моделирования при решении экономических вероятностных задач: методические указания для организации самостоятельной работы по курсу «Теория вероятностей и математическая статистика» студентов направления 080100 «Экономика» профиля «Экономика предприятий и организаций» очной формы обучения. Ч. 2 / В.В. Дежин. Воронеж: ВГТУ, 2013. (№ 151-2013)

33.Дежин В.В. Использование математического моделирования при решении экономических вероятностных задач: методические указания для организации самостоятельной работы по курсу «Теория вероятностей и математическая статистика» студентов направления 080100 «Экономика» профиля «Экономика предприятий и организаций» очной формы обучения. Ч. 3 / В.В. Дежин. Воронеж: ВГТУ, 2013. (№ 152-2013)

34.Дежин В.В. Использование математического моделирования при решении экономических вероятностных задач: методические указания для организации самостоятельной работы по курсу «Теория вероятностей и математическая статистика» студентов направления 080100 «Экономика» профиля

«Экономика предприятий и организаций» очной формы обучения. Ч. 4 / В.В. Дежин. Воронеж: ВГТУ, 2013. (№ 153-2013)

35. Дежин В.В. Решение задач по теории вероятностей и математической статистики с экономическим содержанием: методические указания для организации самостоятельной работы по курсу «Математика» для студентов специальности 080502 «Экономика и управление на предприятиях машиностроения» очной формы обучения. Ч. 1 / В.В. Дежин, Т.А. Надеина. Воронеж: ВГТУ, 2009. (№ 588-2009)

СОДЕРЖАНИЕ

Введение в пакет Maxima……………………………...…..1

Лабораторная работа № 1. Табулирование функции на интервале. Построение графика функции y f x .

Решение уравнения f x 0………………….….……………..6

Лабораторная работа № 2. Решение систем линейных уравнений………………………………...……..……14

Лабораторная работа № 3. Дифференцирование и интегрирование…………………….……………...…………..31

Библиографический список……..……………..………....47