
Методические указания к выполнению лабораторных работ по курсу «Теория вероятностей и математическая статистика» с использованием пакета Maxima. Дежин В.В
.pdf
ФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра высшей математики и физико-математического моделирования
МЕТОДИЧЕСКИЕ УКАЗАНИЯ к выполнению лабораторных работ по курсу
«Теория вероятностей и математическая статистика»
с использованием пакета Maxima для студентов направления 080100 «Экономика» профиля «Экономика предприятий и организаций» очной формы обучения
Часть 1
Воронеж 2013
Составитель канд. физ.-мат. наук В.В. Дежин
УДК 517 Методические указания к выполнению лабораторных ра-
бот по курсу «Теория вероятностей и математическая статистика» с использованием пакета Maxima для студентов направления 080100 «Экономика» профиля «Экономика предприятий и организаций» очной формы обучения. Ч. 1 / ФГБОУВПО «Воронежский государственный технический университет»; сост. В.В. Дежин. Воронеж, 2013. 50 с.
Методические указания предназначены в качестве руководства при выполнении лабораторных работ по курсу «ТВиМС» с использованием пакета Maxima для студентов направления 080100 «Экономика» профиля «Экономика предприятий и организаций» очной формы обучения. Методические указания включают в себя введение, задания к выполнению лабораторных работ, основные понятия и краткие сведения о численных методах, варианты заданий, примеры программ, ссылки на литературу, контрольные вопросы и задания, форму отчетности.
Предназначены для студентов третьего семестра второго курса.
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word и содержатся в файле Э-ТВиМС-Лаб-1.pdf.
Табл. 2. Ил. 7. Библиогр.: 35 назв.
Рецензент канд. физ.-мат. наук, профессор Г.Е. Шунин. Ответственный за выпуск зав. кафедрой д-р физ.-мат. на-
ук, проф. И.Л. Батаронов
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© ФГБОУВПО «Воронежский государственный технический университет», 2013
2

ВВЕДЕНИЕ В ПАКЕТ MAXIMA
Maxima – развитие коммерческой системы Macsyma, разрабатывавшейся в Массачусетском технологическом институте с 1968 по 1982 г. Это была первая универсальная система символьных вычислений и одна из первых систем, основанных на знаниях. Многие из идей, впервые реализованных в Macsyma, впоследствии были использованы в Mathematica, Maple и других системах. Maxima имеет широкий набор средств для проведения аналитических вычислений. Пакет включает также некоторые численные методы, имеет развитые средства построения графических иллюстраций.
Maxima является потомком DOE Macsyma, которая начала своё существование в конце 1960 года в MIT. Macsyma первая создала систему компьютерной алгебры, она проложила путь для таких программ как Maple и Mathematica. Главный вариант Maxima разрабатывался Вильямом Шелтером с 1982 по 2001 год. В 1998 году он получил разрешение на реализацию открытого кода на GPL. Благодаря его умению Maxima сумела выжить и сохранить свой оригинальный код в рабочем состоянии. Вскоре Вильям передал Maxima группе пользователей и разработчиков, которые сохранили ее в рабочем состоянии. На сегодняшний день пакет достаточно активно развивается, и во многих отношениях не уступает таким развитым системам компьютерной математики, как Maple или
Mathematica.
Обозначение арифметических операций в Maxima ничем не отличается от классического представления: + , – , * , /. Возведение в степень можно обозначать двумя способами: ^ или **. Извлечение корня степени n записываем, как степень 1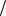 n. Операция нахождение факториала обозначается восклицательным знаком, например 5!. Для увеличения приоритета операции, как и в математике, используются круглые скобки: ().
n. Операция нахождение факториала обозначается восклицательным знаком, например 5!. Для увеличения приоритета операции, как и в математике, используются круглые скобки: ().
Список основных арифметических и логических операторов приведен ниже.
Арифметические операторы:
+ – оператор сложения
– – оператор вычитания или изменения знака * – оператор умножения / – оператор деления
ˆ или ** – оператор возведения в степень
Логические операторы:
< – оператор сравнения меньше > – оператор сравнения больше
<= – оператор сравнения меньше или равно >= – оператор сравнения больше или равно
# – оператор сравнения не равно = – оператор сравнения равно and – логический оператор и or – логический оператор или not – логический оператор не
В Maxima для удобства вычислений имеется ряд встроенных констант. Самые распространённые из них показаны в следующем списке.
Константы: minus – слева (в отношении пределов) plus – справа (в отношении пределов) inf – плюс бесконечность
minf – минус бесконечность
%pi – число π
%e – число e
%i – мнимая единица (
 1) true – истина
1) true – истина
false – ложь
2
Приведем также список основных математических функций доступных в Maxima:
abs – абсолютная величина acos – арккосинус
acosh – обратный гиперболический косинус acot – арккотангенс
acsc – арккосеканс asec – арксеканс asin – арксинус
asinh – обратный гиперболический синус atan – арктангенс
atanh – обратный гиперболический тангенс ceiling – округление до целого с избытком cos – косинус
cosh – гиперболический косинус cot – котангенс
csc – косеканс exp –экспонента fix – целая часть
float – преобразование к формату с плавающей точкой floor – округление до целого с недостатком
log – натуральный логарифм sec – секанс
sin – синус
sinh – гиперболический синус sqrt – квадратный корень tan – тангенс
tanh – гиперболический тангенс
Для хранения результатов промежуточных расчётов применяются переменные. Заметим, что при вводе названий переменных, функций и констант важен регистр букв, так переменные x и X – две разные переменные. Присваивание значения переменной осуществляется с использованием символа : (двое-
точие), например x:5. Если необходимо удалить значение переменной (очистить ее), то применяется метод kill:
kill(x) – удалить значение переменной x;
kill(all) – удалить значения всех используемых ранее переменных.
Зарезервированные слова, использование которых в качестве имён переменных вызывает синтаксическую ошибку: integrate, next, from, diff, in, at, limit, sum, for, and, elseif, then, else, do, or, if, unless, product, while, thru, step.
Все команды вводятся в поле ВВОД, разделителем команд является символ ; (точка с запятой). После ввода команды необходимо нажать клавишу Enter (в wxMaxima нужно нажать Shift+Enter для ее обработки и вывода результата). В ранних версиях Maxima и некоторых ее оболочках (например, xMaxima) наличие точки с запятой после каждой команды строго обязательно. Завершение ввода символом $ (вместо точки с запятой) позволяет вычислить результат введенной команды, но не выводить его на экран. В случае, когда выражение надо отобразить, а не вычислить, перед ним необходимо поставить знак ’ (одинарная кавычка – апостроф). Но этот метод не работает, когда выражение имеет явное значение, например, выражение sin(π) заменяется на значение равное нулю. Две одинарных кавычки, последовательно примененные к выражению во входной строке, приводят к замещению входной строки результатом вычисления вводимого выражения.
Пример 1:
(%i1) aa:1024;
(%o1) 1024
(%i2) bb:19;
(%o2) 19
(%i3) sqrt(aa)+bb;
(%o3) 51
(%i4) ’(sqrt(aa)+bb);
(%o4) bb + √aa
3 |
4 |
(%i5) ”%;
(%o5) 51
После ввода, каждой команде присваивается порядковый номер. В рассмотренном примере 1 введенные команды имеют номера 1–5 и обозначаются соответственно (%i1), (%i2) и т.д. Результат вычисления также имеет порядковый номер, например (%o1), (%o2) и т.д., где i - сокращение от англ. input (ввод), а о - англ. output (вывод). Этот механизм позволяет избежать в последующих вычислениях повторения полной записи уже выполненных команд, например (%i1)+(%i2) будет означать добавление к выражению первой команды выражения второй и последующего вычисления результата. Также можно использовать и номера результатов вычислений, например (%о1)*(%о2). Для последней выполненной команды в Maxima есть специальное обозначение – %.
Пример 2:
(%i3) x:4;
(%o3) 4
(%i4) sqrt(x);
(%o4) 2
(%i5) %^2;
(%o5) 4
Преобразование к форме с плавающей точкой осуществляет функция float.
Пример 3:
(%i2) 3/7+5/3; float;
(%o2) 2.095238095238095
(%i4) float(5/7);
(%o4) 0.71428571428571
Остальные команды, численные методы и приемы работы в системе Maxima будут рассмотрены далее в лабораторных работах.
Замечание. Во время набора программы в пакете Maxima рекомендуется периодически ее записывать. При этом в памя-
ти сохраняются только вводимые команды. Поэтому после загрузки сохраненного файла необходимо заново вводить каждую командную строку.
ЛАБОРАТОРНАЯ РАБОТА № 1
ТАБУЛИРОВАНИЕ ФУНКЦИИ НА ИНТЕРВАЛЕ. ПОСТРОЕНИЕ ГРАФИКА ФУНКЦИИ y f x .
РЕШЕНИЕ УРАВНЕНИЯ f x 0.
Довольно часто возникает задача решения нелинейного уравнения вида f x 0. Данная задача сводится к нахожде-
нию значений аргумента x функции, при котором значение функции равно нулю. При решении этой задачи настоятельно рекомендуется строить график функции f x для приближен-
ного определения корней и интервалов, в пределах которых они находятся (локализация корня).
В курсе «Теория вероятностей и математическая статистика» решение нелинейного уравнения f x 0 применяется
для нахождения квантилей распределения различных статистик при построении доверительных интервалов, проверке статистических гипотез, отсеве грубых погрешностей, проверке значимости коэффициентов уравнения регрессии, проверке адекватности уравнения регрессии, проверке значимости коэффициентов корреляции и т.д. Поясним, что квантилью порядка p распределения случайной величины X непрерывного
типа называется действительное число tp , удовлетворяющее уравнению P X tp p . Это уравнение означает следующее:
вероятность того, что случайная величина X примет значение
5 |
6 |

меньше tp |
равна |
p . Например, для случайной величины, рас- |
||
пределенной |
по нормальному закону |
X N(0,1), квантиль |
||
порядка |
p 0,95 |
(часто встречающаяся величина) равна |
||
u0,95 1,645, |
т.е. |
P X 1,645 0,95. |
Задача нахождения |
|
квантили tp состоит в решении уравнения
tp
x dx p,
которое последовательно сводится к решению нелинейного уравнения f x 0:
(x)tp p ,
(tp) ( ) p,(tp) ( ) p 0.
Задание к выполнению лабораторной работы. Решить нелинейное уравнение f x g x Cx D 0 на отрезке
a, b . Предварительно построить график функции на задан-
ном отрезке и локализовать корень уравнения. Варианты заданий приведены в табл. 1.
Таблица 1
Вари- |
g x |
C |
D |
a, b |
ант |
|
|
|
|
1 |
ex |
-10 |
-35 |
1; 8 |
2 |
x3 0,5x2 |
3 |
6 |
6; 3 |
3 |
arctgx |
-1 |
2 |
1; 8 |
4 |
e x |
11 |
-34 |
8;1 |
5 |
10x |
10 |
-84 |
3; 6 |
6 |
|
sin x |
|
|
|
|
|
|
0,3 |
-1 |
6; |
3 |
|||
7 |
|
ln x |
|
|
|
|
|
|
-5 |
17 |
1;10 |
||||
8 |
cosx |
|
|
-1 |
3 |
2; |
7 |
||||||||
9 |
|
|
tgx |
|
|
|
|
|
|
6 |
-12 |
0,6;1,5 |
|||
10 |
arccosx |
|
|
5 |
-4 |
0,1;1,0 |
|||||||||
11 |
|
|
tgx |
|
|
|
|
|
|
-3 |
10 |
1;10 |
|||
12 |
arcsin x |
|
|
-6 |
4 |
0,1;1,0 |
|||||||||
13 |
|
|
ex2 |
|
|
|
|
|
|
2 |
-10 |
1,0;1,9 |
|||
14 |
arctg |
|
|
|
|
|
|
-2 |
3 |
0; |
9 |
||||
|
x |
|
|
||||||||||||
15 |
3x3 2x2 |
|
|
5 |
-6 |
0,4; 1,3 |
|||||||||
16 |
2ln x 1 x |
|
0 |
-1 |
1,8; 2,7 |
||||||||||
17 |
e x x2 |
|
|
0 |
-2 |
1,0;1,9 |
|||||||||
18 |
|
|
|
|
|
|
|
-3 |
3 |
|
|
|
|||
cos |
|
x 1 |
2 |
|
1; 2 |
|
|||||||||
|
|
|
|
|
|
||||||||||
19 |
|
102x |
|
|
|
|
|
|
8 |
-80 |
3; |
2 |
|||
20 |
lg x 1 x2 |
|
|
0,5 |
0 |
1,0;1,9 |
|||||||||
21 |
tg x |
4 |
|
|
-1 |
-3 |
1,0;1,9 |
||||||||
22 |
tg |
|
|
|
|
|
|
|
|
|
6 |
1 |
0,5;1,4 |
||
|
|
x 2 |
|
|
|||||||||||
23 |
sin x |
3 |
|
|
2,5 |
-2 |
3; |
6 |
|||||||
24 |
2x 2x2 |
|
|
0 |
-1 |
0,1; 0,9 |
|||||||||
Порядок выполнения лабораторной работы
1)Определяем функцию g x .
2)Определяем коэффициенты C и D.
3)Определяем функцию f x .
7 |
8 |
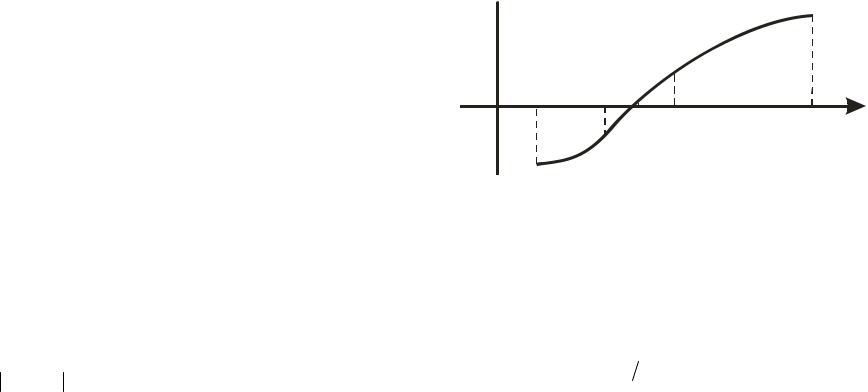
4) Определяем границы отрезка a и b .
5) Строим график. График функции y f x на отрезке
a, b можно построить с помощью функции wxplot2d f (x), x,a,b , y,c,d , опции .
Вместо f x можно записывать f или непосредственное вы-
ражение для функции. Параметр y,c,d можно не задавать,
тогда высота графика выбирается по умолчанию. Опции также не обязательны, однако, для изменения свойств графика их нужно задавать. В данной лабораторной работе желательно на график нанести сетку.
6)По графику находим отрезок локализации корня
a1, b1 , т.е. те значения x, между которыми график функции
пересекает ось Ox .
7) Находим корень уравнения методом половинного де-
ления. |
|
Описание метода |
|
|
|
|
|
||
За начальное приближение x0 |
берут |
середину отрезка |
||
a, b : |
x0 (a b)/ 2. |
Если f x0 0 |
то x0 |
является корнем |
уравнения. Если f x 0 то выбираем ту из половин [a, x0 ], [ x0 , b ] на концах которой функция f x имеет противопо-
ложные знаки. Это означает, что корень лежит в этом промежутке. Затем новый отрезок разделим пополам точкой x1 и выбе-
рем ту половину, на которой лежит корень, и так далее (рис. 1). Если требуется вычислить корень с точностью , то продолжаем процесс до тех пор, пока длина отрезка не станет меньше, то есть xn xn 1 . Достоинства метода: метод очень
прост; метод надежен; сходится к корню для любых непрерывных функций; устойчив к ошибкам округления. Недостаток метода – медленная сходимость.
Для решения уравнения f x 0 |
в пакете Maxima пре- |
|
дусмотрена функция |
find _root . |
Синтаксис вызова: |
find _ root f (x),a,b . Вместо f x можно записывать f или
непосредственное выражение для функции. Поиск корня функции f или выражения относительно переменной x осуществляется в пределах a x b . Для поиска корней используется метод деления пополам.
y
a x1
x2 x0 |
b |
x |
Рис. 1
8) Находим корень уравнения методом Ньютона (мето-
дом касательных).
Описание метода
Если известно хорошее начальное приближение x0 ре-
шения уравнения f x 0, то эффективным методом повы-
шения точности является метод касательных (метод Ньютона). Он состоит в построении итерационной последовательности
xn 1 xn f xn |
f xn , |
n 0,1, 2, , |
(1.1) |
сходящейся к корню уравнения. Сформулируем достаточные условия сходимости метода.
9 |
10 |

Теорема. Пусть f x определена и дважды дифферен-
цируема на a, b , причем |
f a f b 0, а производные f x |
||||||||||
и f x сохраняют знак на a, |
b . Тогда, исходя из начального |
||||||||||
приближения |
x0 a, b , |
удовлетворяющего |
неравенству |
||||||||
f x0 f x0 0, можно |
построить |
последовательность |
|||||||||
(1.1), сходящуюся к единственному на a, b |
решению z урав- |
||||||||||
нения f x 0. |
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
f(x0) |
|
|
|
|
|
x |
) |
|
|
|
|
|
|
|
|
f |
( |
|
|
|
||
|
|
|
|
= |
|
|
|
|
|||
|
|
|
y |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|||
|
f(x1) |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z x2 |
x1 |
|
x0 |
x |
|
|
|||
|
|
Рис. 2 |
|
|
|
|
|
||||
Метод Ньютона допускает простую геометрическую |
|||||||||||
интерпретацию |
(рис. 2). |
Через |
|
точку |
с |
координатами |
|||||
x0, f x0 проводим касательную до пересечения с осью Ox .
Абсцисса точки пересечения x1 будет являться очередным приближением корня уравнения. Через точку с координатамиx1, f x1 тоже проводим касательную к графику функции и получаем очередное приближение x2 . Продолжая далее этот процесс, получим последовательность точек x0, x1, x2, . Из рисунка видно, что эта последовательность сходится к решению z уравнения f x 0. Для оценки погрешности n-
го приближения корня можно воспользоваться неравенством
|
z x |
|
|
M2 |
|
x |
x |
|
2, |
где |
M |
|
max |
|
f x |
|
, |
m |
min |
|
f x |
|
. |
||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
||||||||||||||||||||||||
|
n |
|
|
2m |
|
n |
n 1 |
|
|
|
|
|
2 |
a, ,b |
|
|
|
|
|
1 |
a, b |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M |
2 |
|
|
|
|
|
Таким образом, если |
|
|
x |
x |
|
, то |
|
z x |
|
|
|
|
2 |
|
. Послед- |
||||||||||||
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
n |
|
n 1 |
|
|
|
|
n |
|
|
|
2m |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
||
нее соотношение означает, что при хорошем начальном приближении корня после каждой итерации число верных десятичных знаков в очередном приближении удваивается, т.е. процесс сходится очень быстро.
Достоинства метода: простота, быстрая сходимость, устойчив к погрешностям счета, применим для обширного класса нелинейных уравнений. Недостаток метода – чувствительность к начальному приближению.
Основная функция пакета newton1 предназначена для решения уравнений методом Ньютона. Синтаксис вызова: newton f (x),x,x0,eps . Вместо f x можно записывать непо-
средственное выражение для функции. Поиск корня начинается с начального приближения x x0 и производится, пока не
будет достигнуто условие f x eps , где eps – заданная точ-
ность. Для использования пакета необходимо загрузить его командой load(newton1).
Пример выполнения лабораторной работы
(%i) C:0.5; D:-2;
(%i) g(x):=sin(x/3);
(%i) f(x):=g(x)+C*x+D;
(%i) a:-3; b:6;
(%i) wxplot2d(f,[x,a,b],[gnuplot_preamble, "set grid;"]); (рис. 3)
11 |
12 |
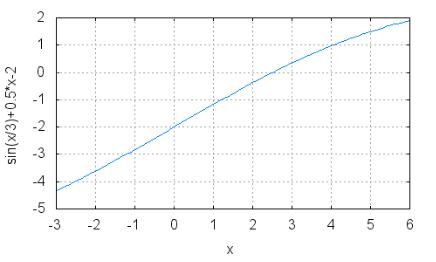
|
Рис. 3 |
(%i) a1:2; |
b1:3; – границы отрезка локализации |
(%i) find_root(f,a1,b1); – метод половинного |
|
|
деления |
(%o) 2.514 |
– корень уравнения |
(%i) load(newton1); |
|
(%i) newton(f(x),x,a1,10^-6); – метод Ньютона
(%o) 2.514 – корень уравнения
Контрольные вопросы
1. В каких случаях в курсе «Теория вероятностей и математическая статистика» применяется решение нелинейного уравнения f x 0?
2. Что такое квантиль?
3.Каков геометрический смысл решения нелинейного уравнения f x 0?
4.Как в пакете Maxima осуществляется построение графика функции одной переменной?
5.С какой целью используется построение графика функции?
6.Для чего и как используется функция find _root ?
7.Для чего и как используется функция newton ?
8.В чем недостатки и преимущества функций find _root
иnewton ?
9.В чем заключается метод половинного деления?
10.В чем заключается метод Ньютона?
Форма отчетности: Отчет должен содержать название лабораторной работы, задание для конкретного варианта, все командные строки, график, отрезок локализации, названия методов, результаты расчетов (три цифры после запятой).
ЛАБОРАТОРНАЯ РАБОТА № 2
РЕШЕНИЕ СИСТЕМ ЛИНЕЙНЫХ УРАВНЕНИЙ
Как известно, обычная система линейных уравнений имеет вид:
a11x1 a12x2 a1mxm b1
a21x1 a22x2 a2mxm b2
...............................................
an1x1 an2x2 anmxm bn
Здесь a11, a12 , …, anm – коэффициенты, образующие матрицу
A, которые могут иметь действительные или комплексные
13 |
14 |
значения; x1, x2 , |
, xm – неизвестные, образующие матрицу- |
|
столбец X ; b1, b2, |
, bn – свободные члены (действительные |
|
или комплексные), |
образующие матрицу-столбец |
B . Эта сис- |
тема может быть |
представлена в матричной |
форме как |
AX B. Существует множество методов решения таких систем, применение которых зависит от вида матриц A и B .
В курсе «Теория вероятностей и математическая статистика» данная работа широко используется при решении нормальной системы уравнений в методе наименьших квадратов для нахождения оценок коэффициентов регрессионной модели. Рассмотрим кратко случай квадратичной аппроксимации. Со-
гласно методу наименьших квадратов коэффициенты много-
члена y x ax2 bx c нужно выбрать такими, чтобы сумма
квадратов отклонений многочлена от заданных значений функции была минимальной. Другими словами, коэффициенты a, b и c должны минимизировать функцию
n
F a,b,c yi y xi 2 . В точке минимума функции F ее
i 1
производные F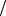 a , F
a , F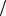 b и F
b и F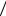 c обращаются в нуль. Дифференцируя F и приравнивая нулю производные, полу-
c обращаются в нуль. Дифференцируя F и приравнивая нулю производные, полу-
чим так называемую нормальную систему
|
|
A a A b A c B |
|
|||
|
|
4 |
3 |
2 |
3 |
|
|
|
A3a A2b A1c B2 , |
|
|||
|
|
A a Ab A c B |
|
|||
|
|
2 |
1 |
0 |
1 |
|
|
|
n |
|
n |
n |
n |
где A0 n 10, |
A1 xi , |
A2 xi2 , |
A3 xi3 , |
A4 xi4 , |
||
|
|
i 1 |
|
i 1 |
i 1 |
i 1 |
n |
|
n |
|
n |
|
|
B1 yi , |
B2 xi yi , B3 |
xi2yi . Здесь xi – фиксирован- |
||||
i 1 |
|
i 1 |
|
i 1 |
|
|
ные значения фактора, yi – случайные значения функции от-
клика.
Задание к выполнению лабораторной работы. Решить систему уравнений из своего варианта тремя способами. Затем решить систему уравнений, исключив строку из системы уравнений своего варианта. Варианты заданий приведены в табл. 2.
|
|
|
|
|
|
|
|
|
|
|
|
|
Таблица 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ва- |
|
|
|
Система уравнений |
|
|
|
|
||||||
ри- |
|
|
|
|
|
|
|
|||||||
ант |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0,4000x1 |
0,0003x2 |
0,0008x3 |
|
0,0014x4 |
|
0,1220 |
|
|||||
|
|
|
0,5000x2 |
|
0,0018x3 |
|
0,0012x4 |
0,2532 |
|
|||||
1 |
0,0029x1 |
|
|
|
||||||||||
0,0055x |
0,0050x |
|
1,4000x |
0,0039x |
4 |
0,9876 |
|
|||||||
|
|
1 |
|
2 |
|
3 |
|
|
|
|
|
|
||
|
0,0082x |
0,0076x |
|
0,0070x |
|
2,3000x |
|
2,0812 |
|
|||||
|
|
1 |
|
2 |
|
|
3 |
|
|
|
4 |
|
|
|
|
|
1,7000x1 0,0003x2 |
|
0,0004x3 |
0,0005x4 |
0,6810 |
|
|||||||
|
|
0,0000x1 |
0,8000x2 |
|
0,0001x3 |
0,0002x4 |
0,4803 |
|
||||||
2 |
|
|
|
|||||||||||
|
0,0003x 0,0002x |
0,1000 0,0000x |
0,0802 |
|
||||||||||
|
|
|
1 |
|
|
2 |
|
|
|
4 |
|
|
|
|
|
0,0005x |
0,0004x |
|
0,0003x |
|
1,0000x |
|
1,0007 |
|
|||||
|
|
1 |
|
2 |
|
3 |
|
|
4 |
|
|
|
||
|
3,0000x1 0,0038x2 |
0,0049x3 |
|
0,0059x4 |
|
1,5136 |
|
|||||||
|
|
0,0011x1 |
2,1000x2 |
|
0,0032x3 |
|
0,0043x4 |
|
1,4782 |
|
||||
3 |
|
|
|
|
|
|||||||||
|
0,0005x 0,0005x |
2 |
1,2000x |
|
|
0,0026x |
|
1,0830 |
|
|||||
|
|
|
1 |
|
|
3 |
|
|
4 |
|
|
|
||
|
0,0022x |
|
0,0011x |
2 |
0,0001x |
|
0,3000x |
|
0,3280 |
|
||||
|
|
1 |
|
3 |
|
|
4 |
|
|
|
||||
|
4,3000x1 0,0217x2 |
|
0,0270x3 |
|
0,0324x4 |
|
2,6632 |
|
||||||
|
|
0,0100x1 |
3,4000x2 |
|
0,0207x3 |
|
0,0260x4 |
2,7779 |
|
|||||
4 |
|
|
|
|
||||||||||
|
0,0037x |
0,0090x |
|
2,5000x |
|
0,0197x |
|
2,5330 |
|
|||||
|
|
1 |
|
2 |
|
|
3 |
|
|
|
4 |
|
|
|
|
0,0027x 0,0027x |
0,0080x |
|
1,6000x |
|
1,9285 |
|
|||||||
|
|
|
1 |
|
|
2 |
|
3 |
|
4 |
|
|
||
15 |
16 |
|
5,6000x1 0,0268x2 |
0,0331x3 |
|
0,0393x4 |
|
4,0316 |
|||
|
|
|
4,7000x2 0,0271x3 |
0,0334x4 |
|
4,3135 |
|||
5 |
0,0147x1 |
|
|||||||
0,0087x |
0,0150x |
3,8000x |
|
0,0274x |
|
4,2353 |
|||
|
|
1 |
2 |
3 |
4 |
|
|
||
|
0,0028x |
0,0090x |
0,0153x |
|
2,9000x |
|
3,7969 |
||
|
|
1 |
2 |
3 |
4 |
|
|
||
|
6,9000x1 0,0319x2 |
0,0390x3 |
0,0461x4 |
|
5,6632 |
||||
|
|
0,0191x1 |
6,0000x2 |
0,0333x3 |
0,0405x4 |
|
6,1119 |
||
6 |
|
|
|||||||
0,0134x |
0,0205x |
5,1000x |
|
0,0348x |
|
6,2000 |
|||
|
|
1 |
2 |
3 |
|
4 |
|
|
|
|
0,0077x |
0,0149x |
0,0220x |
|
4,2000x |
|
5,9275 |
||
|
|
1 |
2 |
3 |
4 |
|
|||
|
8,20001 0,0370x2 |
0,0451x3 |
0,0532x4 |
7,5591 |
|||||
|
|
0,0234x1 |
7,3000x2 0,0396x3 |
0,0477x4 |
8,1741 |
||||
7 |
|
||||||||
0,0179x |
0,0260x |
6,4000x |
|
0,0422x |
|
8,4281 |
|||
|
|
1 |
2 |
3 |
4 |
|
|||
|
0,0124x |
0,0205x |
0,0286x |
|
5,5000x |
|
8,3210 |
||
|
|
1 |
2 |
3 |
4 |
|
|
||
|
9,5000x1 0,0422x2 |
0,0513x3 |
0,0604x4 |
|
9,7191 |
||||
|
|
|
|
|
0,0459x3 |
0,0550x4 |
10,5000 |
||
8 |
0,0278x1 8,6000x2 |
||||||||
0,0224x 0,0315x |
7,7000x |
0,0496x |
10,9195 |
||||||
|
|
|
1 |
2 |
3 |
|
4 |
|
|
|
|
0,0170x |
0,0261x |
0,0351x |
6,8000x |
10,9775 |
|||
|
|
|
1 |
2 |
3 |
|
4 |
|
|
|
10,8000x1 0,0475x2 |
0,0576x3 |
0,0676x4 |
12,1430 |
|||||
|
|
0,0321x1 9,9000x2 |
0,0523x3 |
0,0623x4 |
13,0897 |
||||
9 |
|
||||||||
|
0,0268x 0,0369x |
9,0000x |
0,0570x |
|
13,6744 |
||||
|
|
|
1 |
2 |
3 |
|
4 |
|
|
|
|
0,0215x |
0,0316x |
0,0416x |
|
8,1000x |
13,8972 |
||
|
|
|
1 |
2 |
3 |
|
4 |
|
|
|
12,100x1 0,0528x2 |
0,0639x3 |
0,0749x4 |
14,8310 |
|||||
|
|
0,0365x1 |
11,200x2 |
0,0586x3 0,0697x4 |
15,9430 |
||||
10 |
|
||||||||
0,0312x 0,0423x |
10,300x |
0,0644x |
16,6926 |
||||||
|
|
|
1 |
2 |
3 |
|
4 |
|
|
|
0,0260x 0,0370x |
0,0481x |
9,4000x |
17,0800 |
|||||
|
|
|
1 |
2 |
3 |
|
4 |
|
|
|
|
13,400x1 |
0,0581x2 |
0,0702x3 |
0,0822x4 |
17,7828 |
|
||||||||||
|
|
|
|
12,500x2 0,0650x3 |
0,0770x4 |
19,0599 |
|
||||||||||
11 |
|
0,0408x1 |
|
||||||||||||||
|
0,0356x |
0,0477x |
|
11,600x |
0,0718x |
19,9744 |
|
||||||||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
3 |
|
|
4 |
|
|
|
|
0,0304x |
0,0425x |
|
0,0546x |
10,700x |
20,5261 |
|
|||||||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
3 |
|
|
4 |
|
|
|
|
14,700x1 |
0,0635x2 |
0,0765x3 |
0,0896x4 |
20,9985 |
|
||||||||||
|
|
|
|
13,800x2 |
0,0714x3 0,0844x4 |
22,4406 |
|
||||||||||
12 |
|
0,0452x1 |
|
||||||||||||||
|
|
0,0400x |
0,0531x |
|
12,900x |
0,0793x |
23,5195 |
|
|||||||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
3 |
|
|
4 |
|
|
|
|
0,0349x |
0,0479x |
|
0,0610x |
12,000x |
24,2353 |
|
|||||||||
|
|
|
1 |
|
|
|
2 |
|
|
|
|
3 |
|
|
4 |
|
|
|
|
Порядок выполнения лабораторной работы |
|||||||||||||||
|
1) Решим систему уравнений по правилу Крамера. |
||||||||||||||||
|
|
|
|
|
Описание метода |
|
|
|
|
||||||||
|
Рассмотрим систему уравнений |
|
|
|
|
|
|
||||||||||
|
|
|
a11x1 a12x2 a13x3 a14x4 b1 |
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a21x1 a22x2 a23x3 a24x4 b2 |
(2.1) |
|||||||||||||
|
|
|
a |
x a |
x |
|
a |
x |
a |
|
x |
b |
|||||
|
|
|
|
31 |
1 |
32 |
2 |
|
33 |
3 |
34 |
4 |
3 |
|
|
||
|
|
|
a x a |
42 |
x a |
43 |
x a |
44 |
x b |
|
|
||||||
|
|
|
|
41 |
1 |
2 |
|
3 |
|
4 |
4 |
|
|
||||
с неизвестными x1, x2 , x3 , x4 . Введем обозначения для опре-
делителей.
|
|
|
|
|
a11 |
a12 |
a13 |
a14 |
|
det A |
|
A |
|
|
a21 |
a22 |
a23 |
a24 |
. |
|
|
||||||||
|
|
|
|
|
a31 |
a32 |
a33 |
a34 |
|
|
|
|
|||||||
|
|
|
|
|
a41 |
a42 |
a43 |
a44 |
|
Определитель , составленный из коэффициентов при неизвестных называется определителем данной системы.
17 |
18 |
