2.5. Подходы к определению мер риска для различных распределений вероятности ущерба
Наиболее простой мерой риска является, по-видимому, математическое ожидание ущерба [33]
,
. (2.24)
В более наглядной форме формула (1.15) будет выглядеть так:
-
для НСВ, (2.25)
-
для ДСВ, (2.26)
где
– удовлетворяет условию нормировки.
Если вычисление интеграла в (2.16) на
практике является слишком трудоемкой
задачей, то возможно прибегнуть к
следующему приему: продискретизируем
закон распределения ущерба по оси
абсцисс с шагом дискретизации
и будем считать, что при
закон распределения на этом участке
является линейной функцией (рис. 2.6).
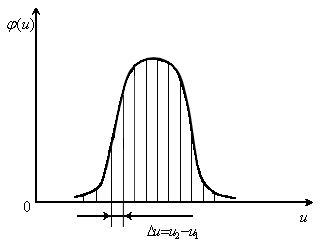
Рис. 2.6. Закон распределения вероятности величины ущерба продискретизированный по оси абсцисс
Введем обозначение
.
Тогда интеграл в формуле (2.25) можно
представить в виде суммы элементарных
рисков (
),
т.е. рисков на интервале
.
Запишется это так:
,
(2.27)
где
.
.
(2.28)
С учётом (2.28), предлагается записать выражения для расчёта рисков, которые позволяют найти его (риска) величину исключительно на интересующем нас интервале, при непрерывном распределении вероятности ущерба:
,
,
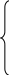(2.29)
.
Учитывая, что при
функцию распределения вероятности
ущерба на этом промежутке можно
рассматривать как линейную и, как
следствие,
,
а также
,
выражения (2.29) можно записать так:
,
,
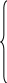(2.30)
. Эта
мера риска, по существу, используется
[32], когда решения принимаются на основании
средних значений, то есть, степень
неопределенности игнорируется. Если
неопределенность состояний среды
значительна, такой способ принятия
решений приводит к большим, иногда
катастрофическим, ошибкам.
Другим примером может служить дисперсия распределения ущерба
,
.
(2.31)
Эта мера риска позволяет уже по существу учитывать неопределенность; на ее основе были построены теории Марковица, а также развившая ее САРМ (Capital Asset Prising Model) – модель Шарпа [15, 34].
Можно ввести также смесь
и
,
,
(2.32)
где
– взвешенный параметр, определяющий
зависимость и имеющий размерность
ущерба.
В современных приложениях активно используется мера ожидаемой полезности [33]
,
,
(2.33)
где
– некоторая вогнутая возрастающая
функция полезности, определяющая
насколько быстро с ростом ущерба растет
его влияние на систему. В качестве
примера такой функции можно взять
.
Тогда риск будет определяться площадью
под следующей кривой:
.
(2.34)
В приложениях активно используется
[33] мера риска
,
называемая VaR (Value
at Risk), которая
представляет собой квантиль распределения
заданного уровня
:
.
(2.35)
Отметим, что меры риска
и
жестко фиксированы, меры
и
обладают некоторой гибкостью: в них
можно выбрать значения параметров
и
,
а меры риска
и
обладают уже значительным запасом
гибкости, что позволяет настраивать
эти меры риска на исследуемую систему.
Также заметим: во всех вышеприведенных
формулах
– есть закон распределения ущерба.
В качестве меры риска возможно также
представить вероятность превышения
ущербом некоторого установленного
значения
:
.
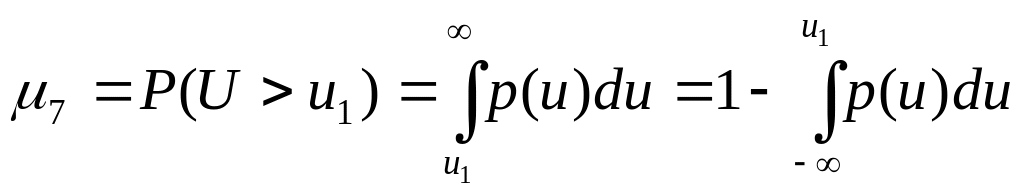(2.36)
При неизменных условиях внешней и внутренней среды риск в системе является константой и определяется в большинстве случаев в литературе как математическое ожидание ущерба [33]. Но с изменением условий, например, с внедрением новых мер защиты или появлением новых алгоритмов взлома, система переходит в новое качественное состояние, которое характеризуется иными параметрами распределения ущерба. Таким образом, можно говорить о том, что изменение ущерба представляет собой случайный процесс, а его математическое ожидание – риск – является случайной величиной.
Пусть
– случайный процесс нанесения ущерба.
Тогда при любом фиксированном
ущерб является случайной величиной,
распределенной по закону
.
В таком случае риск будет представлять
собой:
.
(2.37)
Таким образом, наблюдается широкое
разнообразие способов определения мер
риска. Наиболее простыми из них являются
-
.
Далее приводятся уже более подробные
методики оценки рисков и защищенности.