Можно доказать, что предел суммы, стоящий в правой части равенства равен интегралу

Тогда - двойной интеграл Фурье.

Окончательно получаем:

- представление функции f(x) интегралом Фурье.

Двойной интеграл Фурье для функции f(x) можно представить в комплексной форме:

.

Преобразование Фурье

Определение. Если f(x) – любая абсолютно интегрируемая на всей числовой оси функция, непрерывная или имеющая конечное число точек разрыва первого рода на каждом отрезке, то функция

называется преобразованием Фурье функции f(x).

Функция F(u) называется также спектральной характеристикой функции f(x).

Если f(x) – функция, представимая интегралом Фурье, то можно записать:

Это равенство называется обратным преобразованием Фурье. Интегралы и называются соответственно косинус - преобразование Фурье и синус – преобразование Фурье.

Косинус – преобразование Фурье будет преобразованием Фурье для четных функций, синус – преобразование – для нечетных.

Преобразование Фурье применяется в функциональном анализе, гармоническом анализе, операционном исчислении, теории линейных систем и др.

_{Примеры разложения функций в ряды Фурье}

_{Пример. Периодическая функция ƒ(x) с периодом 2π определяется следующим образом: ƒ(x=х , -π<x ≤ π.}

_{Эта функция – кусочно-монотонная и ограниченная. Следовательно, её можно разложить в ряд Фурье.}

y

x

_{Находим:}

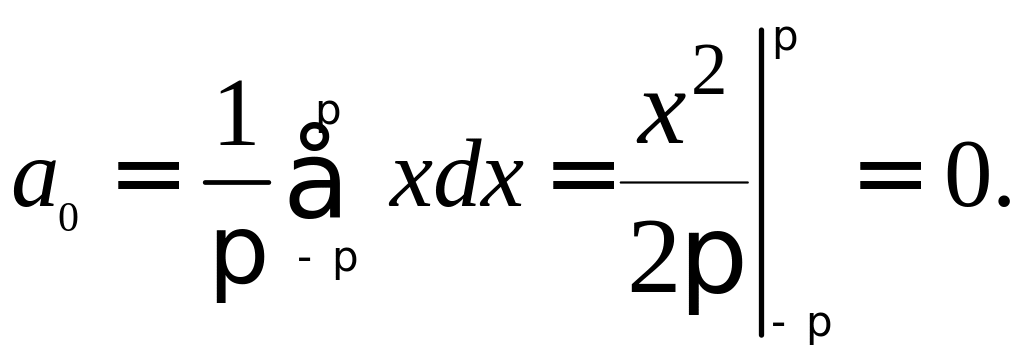
_{Интегрируя по частям, получим:}

_{Таким образом, получаем ряд:}

_{Это равенство имеет место во всех точках, кроме точек разрыва. В каждой точке разрыва сумма ряда равна среднему арифметическому ее пределов справа и слева, т. е. нулю.}

_{Пример. Периодическая функция ƒ(x) с периодом 2π определена следующим образом:}

_{Эта функция кусочно-монотонная и ограничена на отрезке [-π, π]. Вычислим ее коэффициенты Фурье:}

_{Следовательно, для рассматриваемой функции ряд Фурье имеет вид:}

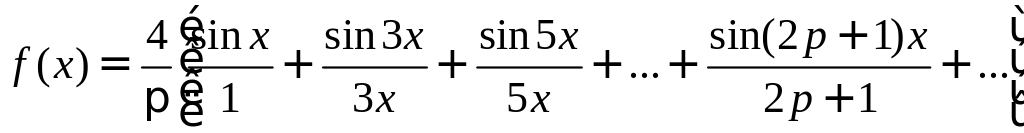
_{Это равенство справедливо во всех точках, кроме точек разрыва.}

_{Замечание о разложении периодической функции в ряд Фурье}

_{Отметим следующее свойство периодической функции ψ(x) с периодом 2π:} , _{каково бы ни было число λ.}

_{Действительно, так как ψ(ξ - 2π) = ψ (ξ) , то, полагая x = ξ - π, можем написать при любых c и d:}

_{В частности, принимая с=- π, d = λ, получим:} , _{поэтому}

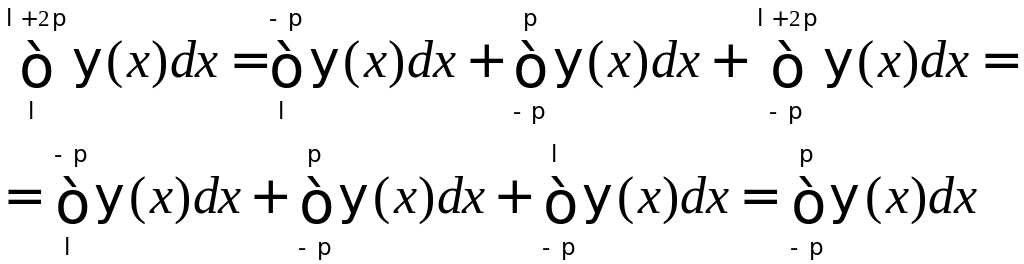
_{Указанное свойство означает, что интеграл от периодической функции ψ(x) по любому отрезку, длина которого равна периоду, имеет всегда одно и тоже значение.}

_{При вычислении коэффициентов Фурье мы можем заменить промежуток интегрирования (-π, π) промежутком интегрирования (λ, λ+2π), т. е. можем положить}

(1)

_{где λ – любое число.}

_{Это следует из того, что функция ƒ(x) является, по условию, периодической с периодом 2π; следовательно и функция ƒ(x)cоsnx, и ƒ(x)sinnx являются периодическими функциями с периодом 2π. В некоторых случаях доказанное свойство упрощает процесс нахождения коэффициентов.}

_{Пример. Пусть требуется разложить в ряд Фурье функцию ƒ(x) с периодом 2π, которая на отрезке 0 <x≤ 2π задана равенством ƒ(x)=х. Эта функция на отрезке [-π, π] задается двумя формулами:}

_{В то же время на отрезке [0, 2π] гораздо проще она задается одной формулой ƒ(x)=х. Поэтому для разложения этой функции в ряд Фурье выгоднее воспользоваться формулами (1), приравняв λ=0.}

_.

_{Следовательно,}

Теория рядов Фурье первоначально была создана для решения дифференциальных уравнений. Поэтому, неудивительно, что ряды Фурье широко используются для поиска решений как обыкновенных дифференциальных уравнений, так и уравнений в частных производных.

Далее рассмотрим приложение рядов Фурье к решению некоторых обыкновенных дифференциальных уравнений, а также к решению трех наиболее популярных типов уравнений математической физики:

• Уравнение теплопроводности

• Волновое уравнение

• Уравнение Лапласа

Пример. Найти решение в виде ряда Фурье дифференциального уравнения с граничными условиями

Решение.

Будем использовать разложение по нечетным гармоникам для построения неоднородного решения уравнения с заданными граничными условиями, можно записать правую часть уравнения в виде ряда . Предположим, что решение уравнения имеет вид Подставляя это в само уравнение, получаем соотношение

Поскольку коэффициенты при каждой гармонике в левой и правой части должны быть равны друг другу, получаем алгебраическое уравнение . Следовательно, решение исходного дифференциального уравнения описывается рядом

Пример. Найти периодические решения дифференциального уравнения , где k − константа, а f (x) − периодическая функция.

Решение.

Представим функцию f (x) в правой части уравнения в виде ряда Фурье:

Здесь комплексные коэффициенты Фурье определяются формулой

Предполагая, что решение уравнения представляется рядом Фурье Найдем выражение для производной: Подставляя это в исходное дифференциальное уравнение, получаем

Поскольку данное равенство справедливо при всех значениях n, то получаем следующее соотношение: 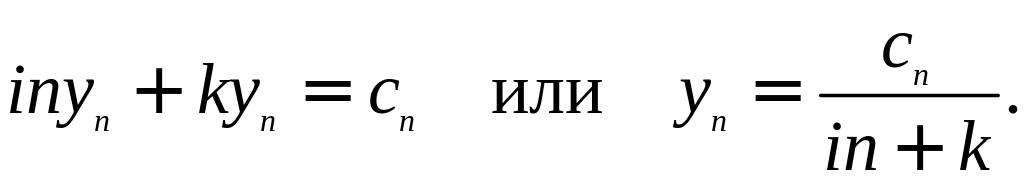Здесь c_n и k − известные числа. Следовательно, решение выражается формулой

Пример.

Используя разложение в ряд Фурье, решить одномерное уравнение теплопроводности с граничными условиями Дирихле: Т=Т₁ при x=0, и Т=Т₂ при x=L. Начальное распределение температуры задано функцией

Решение.

Сначала мы определим стационарное распределение температуры при заданных граничных условиях. Рассмотрим уравнение 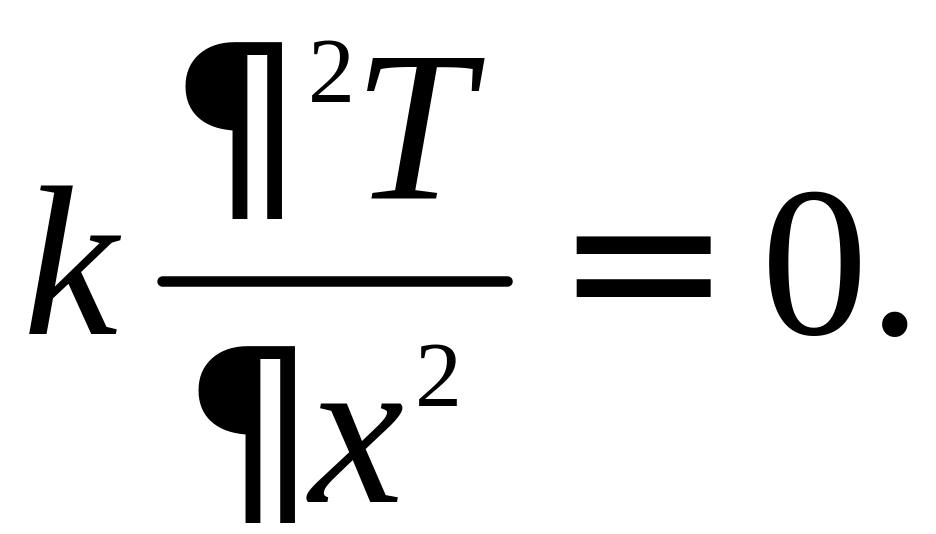Интегрируя его, найдем общее решение: Коэффициенты C₁ и C₂ найдем из граничных условий: Т₀(0)=Т₁, Т₀(L)=Т₂. В результате получаем Построим теперь решение задачи, зависящее от времени. Введем новую переменную Граничные условия для y(x,t) принимают вид: а начальное распределение записывается в форме Принимая во внимание новые граничные условия, будет естественным искать решение в виде разложения по нечетным гармоникам. Тогда где коэффициенты b_n находятся по формуле

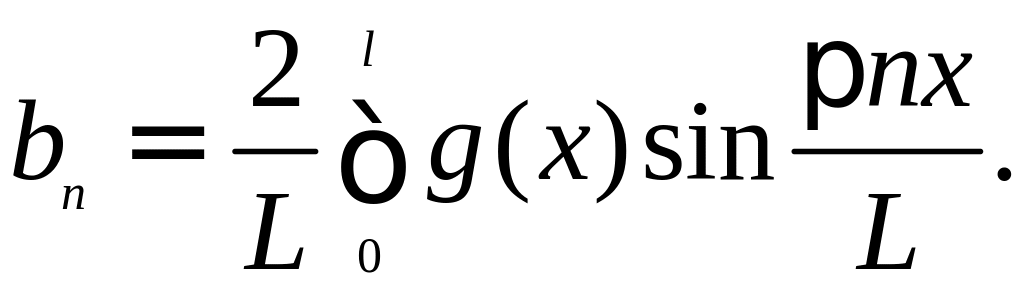
(Мы предполагаем, что эти коэффициенты известны.). Общее решение будем искать в виде ряда с коэффициентами c_n(t), зависящими от времени: 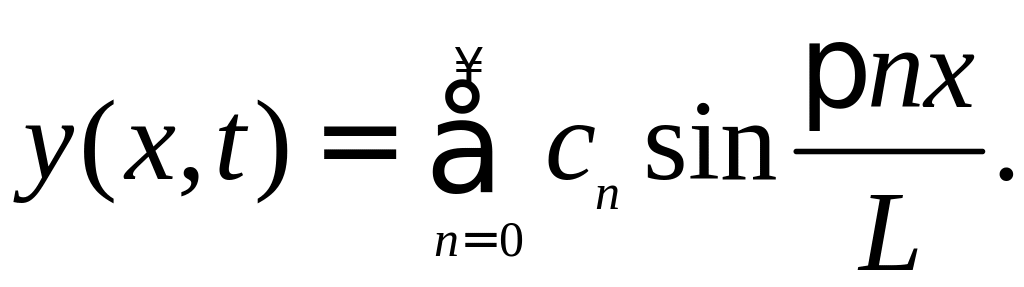Очевидно, что граничные условия y(0,t)=0 и y(L,t)=0 выполняются при любых значениях времени t>0. Начальные условия для c_n(t) имеют вид Подставим эти выражения в уравнение теплопроводности . Тогда Умножим обе части последнего выражения на и проинтегрируем на интервале [0, L], используя соотношения ортогональности .

В результате получаем

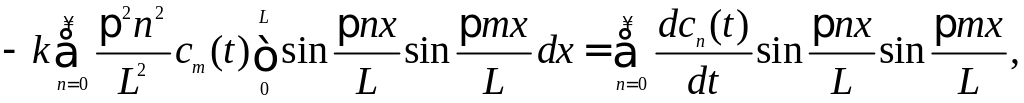или

Решая полученное обыкновенное дифференциальное уравнение, находим c_n (t):

где − постоянная, зависящая от начальных условий. Учитывая, что c_n(0) =b_n, получаем решение для c_n(t) в форме

Следовательно, окончательное решение уравнения теплопроводности выражается формулой

Пример.

Найти решение волнового уравнения для струны с закрепленными концами с граничными условиями u(0,t)=u(L,t)=0. Начальное смещение и скорость заданы в виде

где f(x) и g(x) − некоторые функции, которые считаются известными в данной задаче. При этом должны быть выполнены соотношения

Решение.

Будем искать все периодические решения задачи, в которых разделяются переменные x и t, т.е. в форме Тогда

.

Подставляя это в волновое уравнение, получаем или .

В последней записи функция в левой части зависит только от x, а функция в правой части - только от t. Это возможно, если только обе части уравнения равны некоторой константе. Следовательно,

Если константа α положительная, то, полагая , получим уравнение с общим решением Такое решение не содержит периодических функций по t. Поэтому рассмотрим вариант, когда константа α отрицательна: . В этом случае волновое уравнение расщепляется на два обыкновенных дифференциальных уравнения:

Решая первое уравнение, находим: где C₁ и C₂ − постоянные интегрирования. Учитывая граничные условия, получаем: Тогда

Полагая C₂≠0 (в противном случае мы бы получили тривиальное решение X≡0), находим, что (n − целое число). Следовательно, так называемые собственные значения равны Соответствующие им собственные функции записываются в виде:

При λ=λ_n второе уравнение имеет решение

Таким образом, можно записать, что

Здесь n − целое число, а A_n и B_n − постоянные, зависящие от начальных условий. Теперь мы можем построить общее решение волнового уравнения как линейную комбинацию частных решений:

Предполагая, что этот ряд дифференцируемый, запишем выражение для производной:

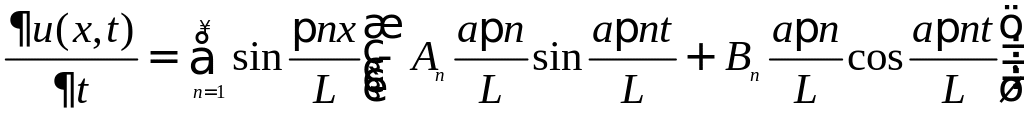
Теперь из начальных условий определим постоянные A_n и B_n:

Видно, что функции f(x) и g(x) следует разложить по ортогональной системе . По формулам для коэффициентов Фурье получаем:

Таким образом, решение волнового уравнения с заданными граничными и начальными условиями имеет вид:

где коэффициенты A_n и B_n определяются приведенными выше формулами. Первый член ряда u₁(x,t) называется основной частотой, остальные члены u_n(x,t) − обертонами или гармониками. Период и частота гармоники определяются формулами

Пример.

Найти решение уравнения Лапласа в круге c граничным условием

Решение.

Будем искать решение в полярных координатах (r, φ). Взаимосвязь между декартовыми и полярными координатами определяется стандартными формулами (рисунок 2):

		Решением задачи будет функция u(r,φ), зависящая от переменных r и φ. Очевидно, u(r,φ) является 2π-периоди–ческой функцией по φ. При этом граничная функция f (x,y) преобразуется в функцию f (φ), зависящую только от пере–менной φ. Уравнение Лапласа в полярных координатах запи–сывается в виде
Рисунок 2

Будем искать решение u(r,φ) в виде ряда Фурье

где коэффициенты Фурье a_n(r) и b_n(r) зависят от радиуса r. Предполагая, что функция u(r, φ) является достаточно гладкой и допускает двойное дифференцирование по r и φ, получаем следующие выражения для производных:

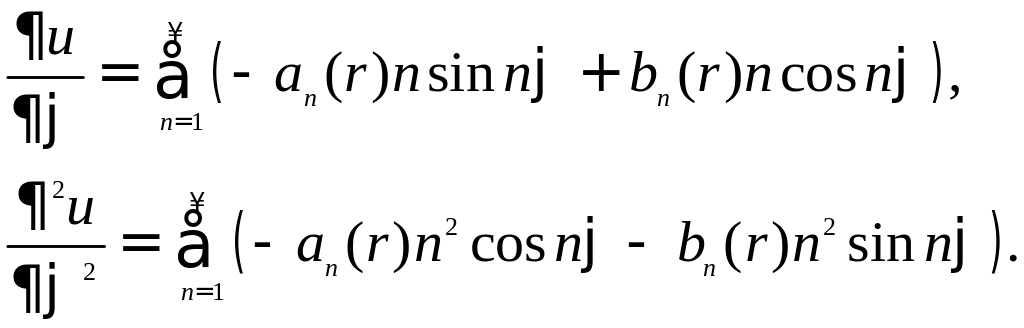
Подставляя это в уравнение Лапласа, находим

Поскольку это выражение равно нулю при всех r и φ, то приходим к выводу, что

Таким образом, мы получили систему обыкновенных дифференциальных уравнений вместо исходного уравнения в частных производных (этот метод был предложен Жозефом Фурье в 1822). Важно, что каждое уравнение в системе решается независимо. Убедимся, что полученным уравнениям удовлетворяют функции вида

Здесь постоянные a_n(r) и b_n(r) находятся из начальных условий к полученным обыкновенным дифференциальным уравнениям. Чтобы сформулировать эти начальные условия, разложим в ряд Фурье функцию , определяющую граничные условия для уравнения Лапласа в полярных координатах. В результате находим

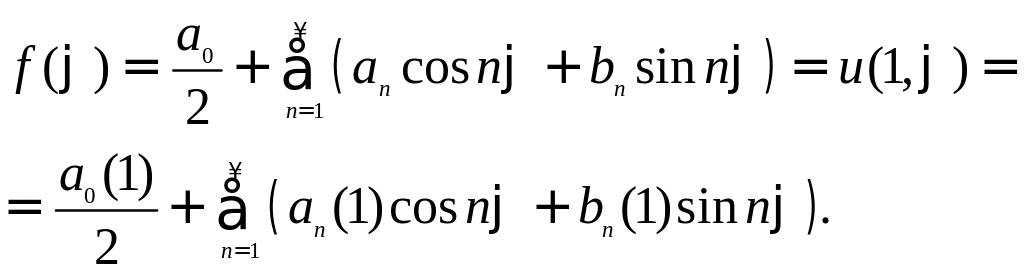
Приравнивая коэффициенты слева и справа при членах cosnφ и sinnφ, получаем соотношения

Следовательно, система обыкновенных дифференциальных уравнений имеет решение

Тогда решение уравнения Лапласа записывается в виде

где α_n, β_n − известные числа, зависящие от граничных условий. Полученный ответ можно упростить. Подставим явные выражения для коэффициентов α_n, β_n:

Заметим, что Поэтому

Используя формулу , можно показать, что выражение в квадратных скобках равно сумме бесконечно убывающей геометрической прогрессии:

Тогда решение будет определяться формулой

Полученное выражение называется интегралом Пуассона для единичного круга.

Библиографический список

1. Пискунов Н.С. Дифференциальное и интегральное исчисления / Н.С. Пискунов. Учебник для втузов. Т.1. - М.: Интеграл-Пресс, 2002. – 214 с.

2. Пискунов Н.С. Дифференциальное и интегральное исчисления / Н.С. Пискунов. Учебник для втузов. Т.2. - М.: Интеграл-Пресс, 2002. – 253 с.

3. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах / П.Е. Данко, А.Г. Попов, Т.Я. Кожевникова: Учеб. пособие для студентов втузов. - М.: Высшая школа, 1986. Ч.2. – 136 с.

Содержание

1. Достаточные признаки разложимости в рад Фурье….............

2. Ряд Фурье для четных и нечетных функций…………………

3. Разложение в ряд Фурье непериодической функции…………

4. Ряды Фурье для функций любого периода ………………..

5. Ряд Фурье по ортогональной системе функций……………

6. Интеграл Фурье…………………………..

7. Преобразование Фурье…………………………………

_{8. Примеры разложения функций в ряды Фурье…………………….}

_{9. Замечание о разложении периодической функции в ряд Фурье……}

10. Библиографический список……………………..

РЯДЫ ФУРЬЕ

МЕТОДИЧЕСКИЕ УКАЗАНИЯ

для студентов специальности