Учебное пособие 800414

….….1.

Однако парные коэффициенты корреляции не характеризуют тесноту связи, так как они вычисляются при случайно изменяющихся значениях других факторов. Действительно, при рассмотрении трех и более случайных величин коэффициенты корреляции любой пары из этих случайных величин могут не дать правильного представления о степени связи между всеми случайными величинами. Это объясняется тем, что на закон распределения вероятностей исследуемой пары случайных величин могут оказывать влияние и другие рассматриваемые случайные величины. Это обстоятельство делает необходимым введение показателей стохастической связи между парой случайных величин при условии, что значения других случайных величин зафиксированы. В этом случае говорят о статистическом анализе частных связей. Используя матрицу (5.31), можно вычислить частные коэффициенты корреляции, которые

показывают степень влияния одного из факторов x на

j

функцию отклика y) при условии, что остальные факторы остаются на постоянном уровне. Формула для вычисления частных коэффициентов корреляции имеет вид

131

где D – определитель матрицы, образованной из матрицы

1j

(5.31) вычеркиванием 1-й строки и j-го столбца. Определители

частные коэффициенты корреляции изменяются от -1 до +1. Значимость и доверительный интервал для коэффициентов

частной корреляции определяются так же, как для коэффициентов парной корреляции, только число степеней свободы вычисляют по формуле

где D – определитель матрицы (5.31).

Множественный коэффициент корреляции дает оценку

тесноты связи между у и совокупностью всех переменных x ,

1

x , ..., x, ..., x .

2 j k

Если число опытов n сравнимо с числом коэффициентов l=k+1, связи оказываются преувеличенными. Поэтому следует исключить систематическую погрешность, физический смысл которой состоит в следующем. Если разность n и l будет уменьшаться, то коэффициент множественной корреляции R будет возрастать и при n-l=0 окажется равным R=+1, а уравнение регрессии превратится в функциональное уравнение

132

гиперплоскости, которая пройдет через все n экспериментальных точек. Однако ясно, что случайный характер переменных процесса при этом не может измениться. В связи с этим требуется оценка значимости коэффициента множественной корреляции.

Значимость коэффициента множественной корреляции проверяется по критерию Стьюдента:

t = ≥ t ; ;m = n − k− 1,

где ̅– среднеквадратичная погрешность коэффициента множественной корреляции, рассчитываемая по выражению

корреляции нулю отвергают и связь считают статистически значимой. Теоретическое (табличное) значение критерия Фишера определяется для выбранного уровня значимости α и

числа степеней свободы m = n-k-1 и m =k .

1 2

Если коэффициент множественной корреляции оказался неожиданно малым, хотя априорно известно, что между

выходом y и входами x ,...,x должна существовать достаточно

1 k

тесная корреляционная связь, то возможными причинами такого явления могут быть следующие:

133

а) ряд существенных факторов не учтен, и следует включить в рассмотрение дополнительно эти существенные входные параметры;

б) линейное уравнение плохо аппроксимирует в действительности нелинейную зависимость = ( ,…, )и

следует определить коэффициенты уже нелинейного уравнения регрессии методами регрессионного анализа;

в) рабочий диапазон рассматриваемых факторов находится в районе экстремума функции отклика – в этом случае следует расширить диапазон изменения входных переменных, а также перейти к нелинейной математической модели объекта.

5.7. Нелинейная регрессия

Используя подходы, изложенные ранее, можно построить практически любые формы нелинейной связи. С этой целью в инженерной практике очень часто используют линеаризующие преобразования.

В таблице приведены часто встречающиеся парные зависимости и линеаризующие преобразования переменных.

Качество преобразования результатов проверяют с помощью уравнения = , + , ∙ , .

134

Функции и линеаризующие преобразования

После вычисления коэффициентов b ′ и b ′, так же как в

0 1

случае линейной зависимости от одного фактора, выполняют обратные преобразования, т.е. по b ′ и b ′ определяют b и b .

Аналогичный подход обычно используют и при множественном нелинейном регрессионном анализе.

135

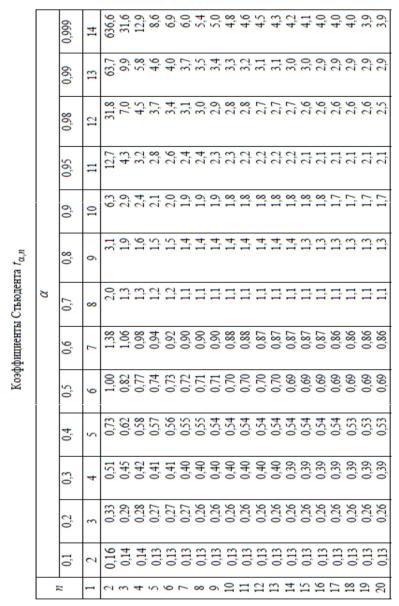
ПРИЛОЖЕНИЕ

136

Продолжение приложения

137

БИБЛИОГРАФИЧЕСКИЙ СПИСОК

1. Белай Г.Е. Организация металлургического эксперимента: учеб. пособие для вузов / Г.Е. Белай, В.В. Дембовский, О.В. Саценко; под ред. В.В. Дембовского. – М.: Металлургия, 1993. -

256с.

2.Теория и техника теплофизического эксперимента: учеб. пособие для вузов / Ю.Ф. Гортышов, Ф.Н. Дресвянников, Н.С. Идиатуллин и др.; под ред. В.К. Щукина. – М.: Энергоатомиздат, 1985. – 360 с.

3.Кафаров В.В. Математическое моделирование основных процессов химических производств: учеб. для вузов / В.В. Кафаров,

М.Б. Глебов. – М.: Высш. шк., 1991. – 400 с.

4.Львовский Е.Н. Статистические методы построения эмпирических формул: учеб. пособие для вузов / Е.Н. Львовский. –

М.: Высш. шк., 1988. – 239 с.

5.Новицкий П.В. Оценка погрешностей результатов измерений / П.В. Новицкий, И.А. Зограф. – Л.: Энергоатомиздат, 1991. – 354 с.

6.Шинк Х. Теория инженерного эксперимента: пер. с англ. / Х.

Шинк. – М.: Мир, 1972. – 381 с.

7.Налимов В.В. Логические основы планирования эксперимента / В.В. Налимов, Т.И. Голикова. – М.: Металлургия, 1980. – 152 с.

8.Горский В.Г. Планирование промышленных экспериментов / В.Г. Горский, Ю.П. Адлер. – М.: Металлургия, 1974. – 264 с.

9.Степнов М.Н. Статистические методы обработки результатов механических испытаний: справочник / М.Н. Степнов. – М.: Машиностроение, 1985. –232 с.

10.Математическая статистика: учеб. для вузов / В.Б. Горяинов, И.В. Павлов, Г.М. Цветкова, О.И. Тескин; под ред. В.С. Зарубина, А.П. Крищенко. – М.: МГТУ им. Н.Э. Баумана, 2001. – 424 с.

11.Большев Л.Н. Таблицы математической статистики / Л.Н. Большев, Н.В. Смирнов. – М.: Наука, 1983. – 416 с.

12.Тюрин Ю.Н. Статистический анализ данных на компьютере / Ю.Н. Тюрин, А.А. Макаров. – М.: ИНФРА-М, 1998. – 528 с.

13.Гмурман В.Е. Теория вероятностей и математическая статистика: учеб. пособие для вузов / В.Е. Гмурман. – М.: Высш.

шк., 2002 . – 479 с.

138

ОГЛАВЛЕНИЕ

Введение……………………………………………………………...3

1.Эксперимент как предмет исследования………………………..4

1.1.Понятие эксперимента……………………………………….4

1.2.Классификация видов экспериментальных исследований.6

2.Методы теории планирования эксперимента…………………13

2.1.Проверка воспроизводимости эксперимента……………..13

2.2.Общие положения ТПЭ…………………………………….15

2.3.Кодирование факторов…………………………………….16

2.4.Рандомизация эксперимента…..…………………………...17

2.5.Метод полного факторного эксперимента………………..18

2.6.Метод дробных реплик……………………………………..25

2.7.Метод ортогонального центрального композиционного планирования……………………………………………………….29

2.8.Метод ротатабельного планирования…………………….34

3.Планирование экспериментов при поиске оптимальных условий……………………………………………………………...43

3.1.Метод покоординатной оптимизации…………………….46

3.2.Метод крутого восхождения……………………………….47

3.3.Симплексный метод планирования………………………..50

139