
Методические указания к практическим занятиям по дисциплине «Теория управления информационной безопасностью распределённых компьютерных систем». Разинкин К.А
.pdfФГБОУ ВПО «Воронежский государственный технический университет»
Кафедра систем информационной безопасности
МЕТОДИЧЕСКИЕ УКАЗАНИЯ
к практическим занятиям № 1, 2 по дисциплине «Теория управления информационной безопасностью распределённых компьютерных систем»
для студентов специальности 090301 «Компьютерная безопасность»
очной формы обучения
Воронеж 2015
Составитель д-р техн. наук. К. А. Разинкин
УДК 004.3
Методические указания к практическим занятиям № 1, 2 по дисциплине «Теория управления информационной безопасностью распределённых компьютерных систем» для студентов специальности 090301 «Компьютерная безопасность» очной формы обучения / ФГБОУ ВПО «Воронежский государственный технический университет»; сост. К. А. Разинкин, 2015. 42 с.
Издание посвящено классическим подходам ТАУ к анализу временных характеристик систем управления на основе передаточных функций и метода переменных состояния с возможностью дискретной аппроксимации векторно-матричных дифференциальных уравнений, описывающих временные характеристики системы, а также особенностям структурного синтеза САУ и построению линейных оптимальных систем с полной обратной связью на основе метода динамического программирования Беллмана в среде Matlab.
В методических указаниях приведены примеры и варианты практических заданий, контрольные вопросы и список рекомендуемой литературы.
Методические указания подготовлены в электронном виде в текстовом редакторе MS Word 2003 и содержатся в файле Разинкин_ПР_ТУИБРКС_1,2.pdf.
Табл. 5. Ил. 17. Библиогр.: 5 назв.
Рецензент д-р техн. наук, проф. И. Я. Львович
Ответственный за выпуск зав. кафедрой д-р техн. наук, проф. А. Г. Остапенко
Издается по решению редакционно-издательского совета Воронежского государственного технического университета
© ФГБОУ ВПО «Воронежский государственный технический университет», 2015
Практическое занятие № 1 Уравнение переходного процесса и передаточная функция
Цель работы: ознакомление с подходами к составлению уравнений динамических режимов звеньев систем автоматического управления (САУ) и нахождения их передаточной функции.
Теоретические сведения
Дифференциальные уравнения физических систем
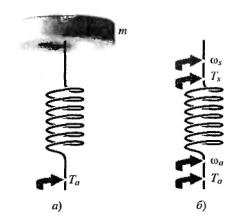
Дифференциальные уравнения, описывающие динамику физической системы, получаются на основании фундаментальных физических законов. Этот метод в равной степени применим к механическим, электрическим, гидравлическим и термодинамическим системам. Рассмотрим крутящуюся систему пружина-масса, изображенную на рис. 1, к которой приложен момент Ta t .
Рис. 1. а) крутящаяся система пружина – масса, б) упругий элемент
Предположим также, что упругий элемент (пружина) обладает пренебрежимо малой массой по сравнению с диском.
Допустим, что нам необходимо измерить момент
Ts t
,
передаваемый массе т. Поскольку согласно допущению пружина не обладает массой, то сумма действующих на нее моментов должна равняться нулю, т. е.
откуда имеем
Ts t
Ta
t
T |
t T t 0, |
a |
s |
. Мы видим, что внешний момент
T |
t |
a |
|
,
приложенный к концу пружины, передается сквозь этот упругий элемент. По этой причине мы будем называть момент сквозной переменной. Аналогичным образом, разность
угловых скоростей концов упругого элемента равна
t s t a t .
Эта разность характеризует угловую скорость одного конца упругого элемента относительно другого, поэтому мы будем называть ее относительной переменной. Подобные рассуждения можно сделать и в отношении большинства известных физических переменных (таких как сила, ток, объем, поток и т. п.). В табл. 1 приведены сводные данные о сквозных и относительных переменных динамических систем. Дифференциальные уравнения линейных динамических элементов с сосредоточенными параметрами приведены в табл. 1. Заметим, что эти уравнения являются идеализированным описанием динамики элементов, т. е. представляют собой всего лишь аппроксимацию их реального поведения (например, когда элемент с распределенными параметрами аппроксимируется линейной моделью с сосредоточенными параметрами).
Обозначение v(t) используется как для напряжения в электрических цепях, так и для скорости поступательного движения в механических системах, поэтому смысл этой переменной следует понимать в контексте каждого дифференциального уравнения. Для описания механических систем используются законы Ньютона, а для электрических систем — законы Кирхгофа. Например, простой механический
2
амортизатор, изображенный на рис. 2 (a), описывается вторым законом Ньютона.
Таблица 1 Сквозные и относительные переменные физических систем
|
|
Сквоз- |
|
Относит |
|
|
|
|
ная |
Интеграл |
ельная |
Интеграл |
|
|
Система |
перемен |
перемен |
|||
|
от СП |
от ОтнП |
||||
|
|
ная |
ная |
|||
|
|
|
|
|
||
|
|
(СП) |
|
(ОтнП) |
|
|
|
|
|
|
|
|
|
|
Электрическая |
Ток, i |
Заряд, q |
Разность |
Потоко- |
|
|
|
|
|
напряж., |
сцепление, |
|
|
|
|
|
v |
|
|
|
|
|
|
21 |
21 |
|
|
Механическая |
Сила, F |
Поступ. |
Разность |
Разность |
|
|
с поступатель- |
|
момент |
скоросте |
перемещений, |
|
|
ным движением |
|
силы, Р |
й, v21 |
y21 |
|
|
Механическая |
Момент, |
Угловой |
Разность |
Разность |
|
|
с вращательным |
T |
момент, h |
угловых |
угловых |
|
|
движением |
|
|
скоросте |
перемещений, |
|
|
|
|
|
й, 21 |
21 |
|
|
Гидравлическая |
Объёмн. |
Объём, |
Разность |
Момент |
|
|
|
расход |
V |
давлений |
давления, 21 |
|
|
|
жидкост |
|
, P21 |
|
|
|
|
и, Q |
|
|
|
|
|
|
|
|
|
|
|
|
Тепловая |
Теплово |
Тепловая |
Разность |
|
|
|
|
й поток, |
энергия, H |
темпер. |
|
|
|
|
q |
|
21 |
|
|
|
|
|
|
|
|
|
3
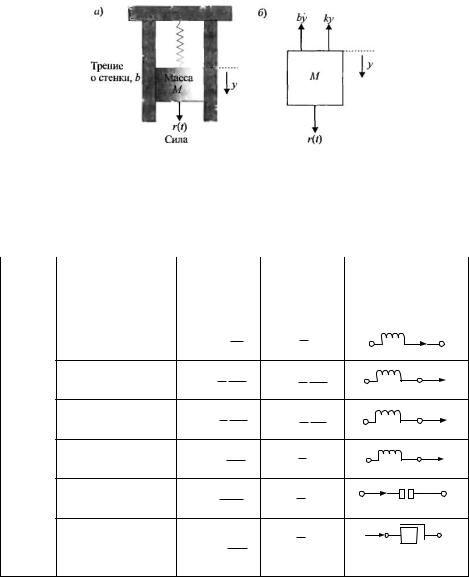
Рис. 2. (а) Система пружина-масса с демпфированием; (б) Условное обозначение
Таблица 2 Дифференциальные уравнения идеальных элементов
Тип |
Физический |
Дифф. |
Энергия |
Обозначение |
|||||||||
элеме |
элемент |
уравнен. |
E, или |
|
|
|
|
|
|||||
нта |
|
|
|
|
мощность |
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Энергетическая |
|
|
di |
|
1 |
|
2 |
v |
|
i |
|
|
|
|
v |
L |
|
|
|
|
|
|
|
L |
|
|
|
|
|
E |
|
Li |
|
|
2 |
|
v |
1 |
||
|
|
21 |
|
|
|
|
|
|
|||||
|
индуктивность |
|
dt |
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Индуктивные накопители
Пружина
сжатия
Пружина
кручения
Инерция
жидкости
Электрическая
ёмкость
Масса с линейным
перемещением
v |
|
|
1 dF |
||
|
|
|
|||
21 |
|
k |
dt |
||
|
|
|
|||
|
|
|
1 dT |
||
21 |
2 dt |
||||
|
|
||||
|
|
|
|||
P |
I |
dQ |
|||
|
|||||
|
21 |
|
|
dt |
|
|
|
|
|
||
i C |
dv |
||||
|
21 |
||||
|
|
|
|
||
|
|
|
|
dt |
|
F M |
dv |
||||
2 |
|||||
|
|
|
|
||
|
|
|
|
dt |
|
|
1 |
F |
2 |
|
E |
|
|||
2 |
k |
|||
|
||||
E
1 T 2
2 k
E1 IQ2
2
E |
1 |
2 |
|
Cv |
|
|
2 |
21 |
|
|
E1 Mv2
2 2
|
|
k |
v |
|
|
v |
|
|
1 |
F |
|
2 |
|
|
|||
|
|
|
|
|
k |
|
|
|
|
|
|
2 |
|
1 |
|
T |
|
|
I |
Q |
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P1 |
|
v |
i |
|
C |
|
v |
|
2 |
|
|
|
1 |
||
|
|
|
|
|||
|
F |
|
|
|
|
|
|
|
|
M |
|
const |
|
|
v |
2 |
v |
1 |
|
|
4
|
|
|
|
|
|
|
|
Продолжение табл. 2 |
|||||||||||
Тип |
Физический |
Дифф. |
Энергия |
Обозначение |
|||||||||||||||
элеме |
элемент |
уравнен. |
E, или |
|
|
|
|
|
|
|
|
|
|||||||
нта |
|
|
|
|
мощность |
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Вращающаяся |
T J |
d 2 |
E |
1 |
J |
2 |
T |
|
|
|
J |
|
|
|
||||
|
масса |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
dt |
|
|
2 |
|
2 |
|
2 |
|
|
1 |
const |
|||||
накопители |
|
|
|
|
|
|
|
|
|
|
|||||||||
Гидравлическая |
Q C |
|
dP21 |
E |
1 |
|
|
|
2 |
Q |
|
|
|
|
C f |
|
|
||
ёмкость |
f |
dt |
2 |
C f P21 |
|
|
P2 |
|
|
|
P |
||||||||
|
|
|
|
|
|
|
|
|
|
|
1 |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тепловая |
q C |
d |
E Ct 2 |
|
q |
|
|
|
C |
|
|
|
|||||||
Ёмкостные |
ёмкость |
|
|
|
|
|
|
|
|
|
|
|
|
|
t |
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
const |
||||
|
t |
dt |
|
|
|
|
|
|
|
|
2 |
|
|
1 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Электрическое |
i 1 v |
|
|
|
1 |
|
|
|
|
|
R |
|
i |
|
|
||||
P |
|
|
v2 |
|
v 2 |
|
|
|
|
|
|
|
|||||||
сопротивление |
|
|
|
|
|
|
|
|
|
|
v1 |
||||||||
R |
21 |
|
|
|
R |
21 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Амортизатор |
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
линейного |
F bv |
P bv21 |
F |
|
v |
2 |
|
b |
|
v1 |
||||||||
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
действия |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Схематическое изображение динамики массы М показано на рис. 2 (б). В этом примере мы будем считать, что трение груза о стенки является вязким, т. е. сила трения линейно зависит от скорости движения груза. В действительности сила трения может описываться более сложной зависимостью. Например, трение о стенки может быть кулоновым. Сила кулонова, или сухого, трения является нелинейной функцией скорости груза, которая имеет разрывный характер вблизи нулевой скорости. Для хорошо смазанной гладкой поверхности наиболее адекватным является вязкое трение, поэтому в данном и всех последующих примерах, где рассматривается механическая система, состоящая из массы и пружины, будет использоваться именно вязкое трение. В соответствии со вторым законом Ньютона, суммируя все силы, действующие на массу М, запишем:
M |
d 2 y t |
|
b |
dy t |
|
ky t r t , |
(1) |
|
dt2 |
dt |
|||||||
|
|
|
|
|||||
5
где k— коэффициент упругости пружины, а b — коэффициент трения. Уравнение (1) есть дифференциальное уравнение второго порядка с постоянными коэффициентами.
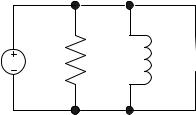
Точно так же можно с помощью закона Кирхгофа для токов описать электрическую RCL-цепь, представленную на рис. 3.
r t
DC
R
L
v ( t )
 C
C
Рис. 3. RCL-цепь
В результате мы получим следующее интегродифференциальное уравнение:
v t |
|
dv t |
|
|
1 |
t |
|
||
C |
|
|
v t dt r t |
(2) |
|||||
|
|
|
|
||||||
R |
|
dt |
|
L 0 |
|
||||
Решение дифференциального уравнения, описывающего динамический процесс, может быть получено классическим методом — путем интегрирования с использованием неопределенных коэффициентов. Например, если груз сместить в начальное положение y(t) = y(0) и затем отпустить,
то движение такой недодемпфированной системы
описывается выражением
y t K1e |
t |
sin 1t 1 |
|
(3) |
|
1 |
|||||
|
|
|
|
Аналогичное решение имеет место для напряжения v(t) RLC-цепи, если она находится под воздействием постоянного тока r(t) = I:
v t K |
e 2t cos t |
2 |
|
(4) |
2 |
2 |
|
|
6

Типичный характер изменения напряжения в недодемпфированой RLC-цепи показан на рис. 4.
Рис. 4. Типичный характер изменения напряжения в недодемпфированной RCL-цепи
Чтобы обнаружить более близкое сходство между дифференциальными уравнениями механических и электрических систем, перепишем уравнение 1 относительно
скорости v t dy t .
dt
В результате получим
|
dv t |
t |
|
||
M |
bv t k v t dt r t |
(5) |
|||
dt |
|
||||
|
0 |
|
|||
Сразу же можно отметить эквивалентность уравнений (5) и (2), только в одном из них переменная v(t) обозначает скорость, а в другом — напряжение. Поэтому данные переменные обычно называют переменными-аналогами, а соответствующие системы — подобными системами. Следовательно, закон изменения скорости будет также иметь вид (4), которому соответствует кривая на рис. 4. Понятие подобия систем является очень полезным и эффективным методом при моделировании. Аналогия между напряжением и
7
скоростью, часто называемая аналогией сила-ток, вполне естественна, поскольку она характеризует связь между подобными сквозными и относительными переменными электрических и механических систем. Однако часто используется и другая аналогия, называемая аналогией силанапряжение, при которой рассматривается подобие скорости и тока.
Подобные системы с одинаковыми решениями можно обнаружить среди электрических, механических, тепловых и гидравлических систем. Наличие таких систем позволяет исследователю распространить решение, полученное для одной системы, на все подобные системы, описываемые аналогичными дифференциальными уравнениями. Следовательно, результаты, полученные, скажем, при анализе и синтезе электрических систем, сразу можно применить для представления о поведении гидравлических, тепловых и механических систем.
Преобразование Лапласа
Возможность линеаризации физических систем предоставляет в распоряжение исследователя аппарат преобразования Лапласа. Метод преобразования Лапласа позволяет заменить достаточно сложное решение дифференциальных уравнений относительно простым решением алгебраических уравнений. Определение реакции системы на входное воздействие подразумевает следующие действия:
1.Получение дифференциальных уравнений.
2.Преобразование по Лапласу этих дифференциальных уравнений.
3.Решение полученных алгебраических уравнений относительно переменной, представляющей интерес.
Для того чтобы функция |
f t |
имела преобразование |
Лапласа, достаточно, чтобы выполнялось условие
 f t
f t  e 1t dt ,
e 1t dt ,
0
8
