Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Специализированные исполнительные устройства (Динамический расчет робототехнических систем). Литвиненко А.М., Машаров А.В

.pdf

Скачиваний:

Добавлен:

01.05.2022

Размер:

1.18 Mб

Скачать

☆

1 / 41 2 3 4 > Следующая >>>

МИНИСТЕРСТВО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Воронежский государственный технический университет

А.М. Литвиненко А.В. Машаров

СПЕЦИАЛИЗИРОВАННЫЕ ИСПОЛНИТЕЛЬНЫЕ УСТРОЙСТВА (ДИНАМИЧЕСКИЙ РАСЧЕТ РОБОТОТЕХНИЧЕСКИХ СИСТЕМ)

Утверждено Редакционно-издательским советом университета в качестве учебного пособия

Воронеж 2004

УДК 658.52.011.56.012.3.005:658.012.011.56

Литвиненко А.М., Машаров А.В. Специализированные исполнительные устройства (Динамический расчет робототехнических систем): Учеб. пособие. Воронеж: Воронеж. гос. техн. ун-т, 2004. 120 с.

В учебном пособии рассмотрены вопросы динамического расчета робототехнических систем.

Издание соответствует требованиям Государственного образовательного стандарта высшего профессионального образования по направлению 220200 «Автоматизация и управление », специальности 220201 «Управление и информатика в технических системах», дисциплине «Системы» управления роботами.

Учебное пособие подготовлено на магнитном носителе в текстовом редакторе MS WORD97.0 и содержится в файлах ―ВВЕДЕНИЕ.doc‖, ―ГЛАВА 1.doc‖, ―ГЛАВА 2.doc‖, ―ГЛАВА

3.doc‖.

Табл. 1. Ил. 50. Библиогр.: 37 назв.

Научный редактор д-р техн. наук, проф. В.Л.Бурковский

Рецензенты: НИИ Механотроника-Альфа (ген.директор канд.техн.наук, доц Э.Г. Кузнецов)

д-р техн. наук, проф Ю. С. Сербулов (ВГТА)

©Литвиненко А.М., Машаров А.В.,

2004

©Оформление. Воронежский государственный технический университет, 2004

ВВЕДЕНИЕ

К методам динамического управления обычно относят такие, при которых формирование управляющих сигналов осуществляется с учетом уравнений динамики манипулятора. При этом за счет усложнения управления удается преодолеть негативное влияние нелинейностей и перекрестных связей, повысить качество процесса управления, обеспечить его устойчивость независимо от конкретной траектории. Такое управление приобретает особенно важное значение для манипуляторов, снабженных высоко моментными без редукторными электродвигателями, поскольку в этом случае неприемлемы методы расчета, основанные на разделении каналов управления.

При анализе движения манипулятора, кинематическая цепь которого содержит замкнутые контуры, или при выполнении с помощью манипулятора различных механических операций, таких, как сборка, обработка поверхности. Для анализа динамики манипуляционных механизмов в подобных случаях более эффективными оказываются модели движения в форме уравнений Лагранжа, а также применение принципа наименьшего принуждения Гаусса. Другой причиной, способствовавшей широкому применению этих методов, является поиск подходов, позволяющих получить численные алгоритмы моделирования движения сложных механизмов, наиболее эффективные с точки зрения затрат машинного времени.

ЛАБОРАТОРНАЯ РАБОТА №1

ИССЛЕДОВАНИЕ НЕЛИНЕЙНОСТИ ВИДА ЛЮФТ В БЛОКЕ ПЕРВОГО ПРИВОДА ПОВОРОТА РОБОТАМАНИПУЛЯТОРА.

1. ЦЕЛЬ РАБОТЫ:

Составить структурную схему двигателя постоянного тока с независимым возбуждением первого привода поворота (с постоянным моментом инерции).

Провести исследование модели электромеханической системы первого привода поворота робота-манипулятора с учетом нелинейности вида люфт.

Количественно оценить показатели качества: быстродействие, перерегулирование, максимальная динамическая ошибка.

2. ОБОРУДОВАНИЕ.

ПК с программным пакетом MatLab.

3.КРАТКИЕ ТЕОРЕТИЧЕСКИЕ СВЕДЕНИЯ.

В системах автоматического управления встречаются нелинейности самого различного типа. Нелинейные звенья можно классифицировать по самым различным признакам: симметрии, гладкости, однозначности, непрерывности харак-

теристик. Рассмотрим типовое нелинейное звено с многознач-

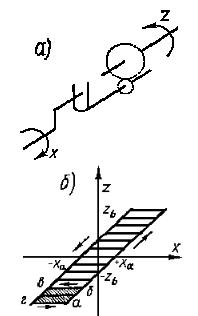
ными характеристиками, на примере звена типа « люфт». Одна из нелинейностей, наиболее часто встречающихся в механических системах, связана с наличием зазоров в системе передачи. В моделях нелинейности типа «люфт» зависимость между положением ведущего x и ведомого z валов неоднозначна. Характеристика, выражающая зависимость между положениями ведущего и ведомого валов, показана на рис.1 б

Рис.1 a – входной и выходной валы, 1 б - характеристика нелинейности вида люфт

Каждому положению ведущего вала x соответствует множество положений ведомого вала z, лежащее в пределах k(x-xa)≤ z ≤ k(x+xa). Выбор того или иного из возможных положений определяется минимальным или максимальным по-

ложением z, предшествовавшим рассматриваемому моменту времени.

Аналитически, характеристика звена типа «люфт» выражается должно образом:

0	при x	0	и	kxa	kxa ;
	при x	0	и	kxa	kxa	;
z
						(1.1)
	при x	0	и	kxa ;
kx
	при x	0	и	kxa ;

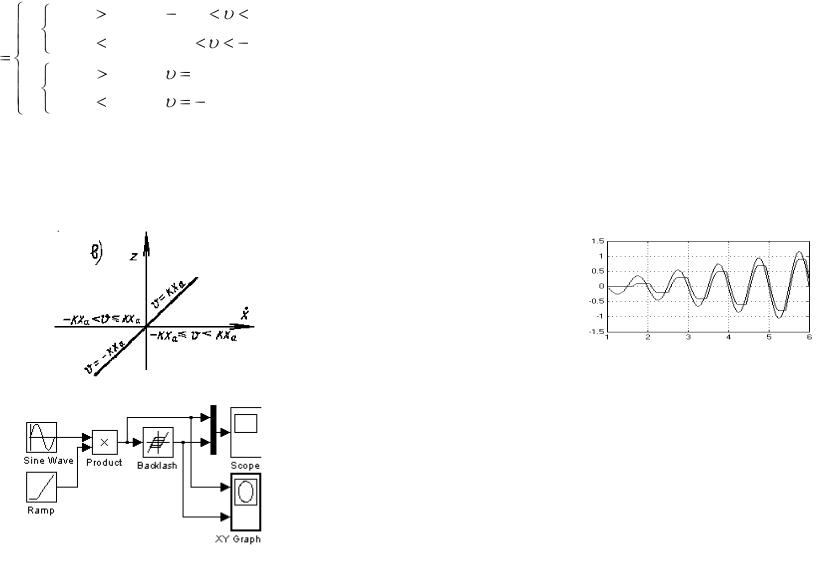
где x = dx/dt и ż = dz/dt, υ = kx-z

Зависимость z от x, выражаемая уравнением 1.1, для различных значений υ представлена на рис.1 в.

Рис. 1 в

Рис. 2 Структурная схема моделирования нелинейности вида люфт

Параметры блока люфта (Backlash) в Simulink:

1.Deadband width – Ширина люфта.

2.Initial output – Начальное значение выходного сигнала.

Сигнал на выходе будет равен заданному значению Initial output, пока входной сигнал при возрастании не достигнет значения (Deaband width)/2 (где U – входной сигнал), после чего выходной сигнал будет равен U-(Deaband width)/2. После того как, произойдет смена направления изменения входного сигнала, он будет оставаться неизменным, пока входной сигнал не изменится на величину (Deaband width)/2, после чего выходной сигнал будет равен U+(Deaband width)/2.

Рис. 3 Результат моделирования нелинейности вида люфт

Динамика линеаризованного привода, механическая часть которого может быть принята абсолютно жесткой, описывается следующими уравнениями:

k y Ay ( p) Д .Х (t)		(t),
k Д В Д ( р)М Д (t)		Д .Х . (t)
J Д p	Д (t) M Д (t)	M Н . Д
Д (t)	(t)i p ,
M H (t)	M H . Д i p k П. Д .

Д (t),

(t),

(1.2)

Здесь Ау(р), ВД(р) — операторные многочлены, характеризующие инерционность усилителя и двигателя привода; kу, kД — коэффициенты пропорциональности; р — оператор дифференцирования по времени; ωД.Х — координата, имеющая размерность угловой или линейной скорости и зависящая от управляющего воздействия v(t); MД (t) — момент (усилие), развиваемый двигателем; MН(t) — суммарный момент (усилие), создаваемый нагрузкой; MН.Д(t) — момент (усилие) нагрузки MН(t), приведенный к валу двигателя; Jд — момент инерции или масса перемещающихся частей двигателя;

ω= q, Д

qД — угловые либо линейные скорости переме-

щения объекта, управления и двигателя; qД- — угловое или линейное перемещение вала двигателя; ip — передаточное число механической передачи, передающей движение от двигателя к объекту управления (ip l);

	1	при М Н	0,
		при М Н	0,
kП. Д			(1.3)
		при М Н	0,

η—коэффициент полезного действия механической передачи (к.п.д.).

Момент нагрузки MН(t) в уравнениях (1.2) может быть представлен в виде:

М Н (t) М ДИН (t) МТ (t) МСТ (t) М В (t). (1.4)

Здесь Мдин—динамический момент, обусловленный инерционностью нагрузки; Мт — момент сопротивления, создаваемый силами трения на валу нагрузки; Мст — момент сопротивления, определяемый весом нагрузки;MB— внешний момент.

Приведенный к валу нагрузки момент, развиваемый двигатель (момент на выходе привода),

M П			ipkП. Д М Д ,		(1.4)
где
	1		при М Д		0,
				Д
kП . Д					(1.5)
			при М Д	Д	0;
значение коэффициента			kП. Д определяется аналогично
выбору коэффициента kП. Д		в соотношении для приведения

момента нагрузки Мн в формулах (1.2), причем момент Мн определяется соотношением (1.4) с Мт = 0.

Первое уравнение в (1.2) — это уравнение усилителя, второе — уравнение двигателя. Для большинства двигателей

операторный многочлен Вд (р) имеет вид
ВД ( р) Т Д р 1,	(1.6)

где Тд — постоянная времени двигателя. Третье уравнение (1.2) является уравнением моментов на валу двигателя.

4.ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ.

-Составить структурную схему MATLAB двигателя постоянного тока с постоянным моментом инерции и моментом нагрузки согласно математической модели 1.2.

-Произвести расчѐт постоянных времени двигателя, исходя из параметров двигателя.

Т э	L	(1.7)

	R
	R

- электромагнитная постоянная двигателя, характеризует инерционность электрических процессов в якорных двигателях;

J R	Тм	(1.8)

Ce Cм
Ce Cм

электромеханическая постоянная времени, характеризует инерционный переходный процесс механического движения двигателя.

- Определить передаточную функцию объекта контура

тока

		1

W ( p)		R		(1.9)
W ( p)	L			(1.9)
	L	p	1

	R
	R

L – индуктивность обмоток двигателя постоянного тока, R – сопротивление двигателя.

-Добавить в структурную схему MATLAB нелинейность типа люфт.

-Провести исследование показателей качества: быстродействие, перерегулирование, максимальная динамическая ошибка

Варианты:

	L,	R,O					Deadban
	м			1 / J н	Се	См
		м					d width
	Гн


1	0,		100		0,0	0,0	0,01*
	5				86	86	U вх

2	0,		200		0,0	0,0	0,04*
	3				53	53	U вх

3	0,		300		0,0	0,0	0,05*
	8				45	45	U вх

4	1		400		0,0	0,0	0,06*
					32	32	U вх

				68
	1,				0,0	0,0	0,07*
5				500
	2				23	23	U вх

6	1,		600		0,0	0,0	0,08*
	4				14	14	U вх

-Оформить отчет по лабораторной работе. Отчет должен содержать:

-формулировку цели работы

-основные формулы и структурные схемы

-найденные показатели качества

5.КОНТРОЛЬНЫЕ ВОПРОСЫ.

-Напишите передаточную функцию объекта контура тока ДПТ.

-Какую характеристику имеет звено с «люфт»

-Приведите пример механической модели люфта.

ЛАБОРАТОРНАЯ РАБОТА №2

ИССЛЕДОВАНИЕ НЕЛИНЕЙНОСТИ ВИДА ЗОНА НЕЧУВСТВИТЕЛЬНОСТИ В БЛОКЕ ВТОРОГО ПРИВОДА ПОВОРОТА РОБОТА-МАНИПУЛЯТОРА.

1.ЦЕЛЬ РАБОТЫ

Провести исследование второго привода поворота робо- та-манипулятора в модели с блоком вычисления моментов нагрузки. Провести исследование нелинейностей вида «зона нечувствительности». Количественно оценить показатели качества переходного процесса: быстродействие, перерегулирование, максимальная динамическая ошибка.

2. КРАТКИЕ ТЕОРEТИЧЕСКИЕ СВЕДЕНИЯ

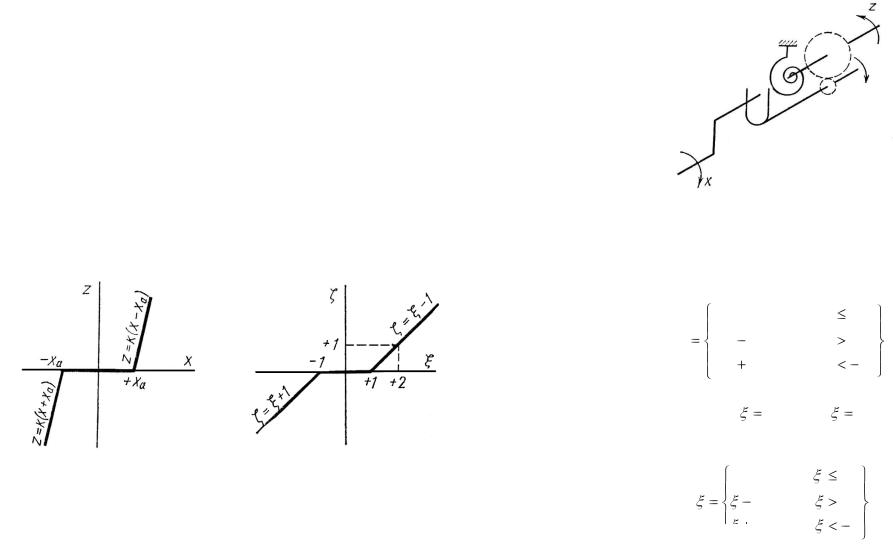
Характеристики звена типа «зона нечувствительности» показаны на рис. 1.

Рис. 1 Такими схемами обладают некоторые схемы электрон-

ных, магнитных и гидравлических усилителей в области малых входных сигналов. Простейшей70 механической моделью

зоны нечувствительности является система двух валов с пружинным возвратом ведомого вала в нейтральное положение при наличии участка свободного хода (люфта) в системе передачи. Такое соединение двух валов показано схематически на рис. 2.

Рис. 2

Здесь зона свободного хода ведущего вала имеет ширину 2xa . Характеристика звена (рис. 1,а) выражается следующими уравнениями:

		0	при		x	xa ;
z	k (x	xa )	при		x	xa ;
	k (x xa ) при x					xa .
Вводя переменные		x / xa		и		z /(kxa ) , получим
нормированную характеристику:
		0	при			1;
		0	при			1;
		1	при			1;
	71 1		при			1.

Уравнения Лагранжа II рода, которыми, как известно, можно описать любую голономную систему с n степенями свободы, имеет вид

d	L	L	Qk	, k 1, , n,	(4.1)

dt	qk	qk
dt	qk	qk

где L=T–П – функция Лагранжа системы, Т – кинетическая энергия системы, П – потенциальная энергия системы, qk

– обобщенные координаты, qk – обобщенные скорости, Qk –

обобщенные силы. Рассмотрим компоненты формулы (4.1) для манипулятора, представляющего собой разомкнутую кинематическую цепь из n звеньев, с учетом объекта манипулятора. Кинетическая энергия манипулятора равна сумме кинетических энергий его звеньев и объекта манипулирования:

	n
T	Ti TГ	(4.2)
	i 1

Здесь Ti – кинетическая энергия i-го звена, ТГ – кинетическая энергия груза (объекта манипулирования).

Обозначим через	r i	(xi	,1)*	(xi	, xi	, xi	,1)*	радиус-
	p	p		1 p	2 p	3 p

вектор некоторой точки i-го звена в системе координат, связанной с р-м звеном (i=1, …, n; p=0, 1, …,n), и положим

r i r i . Тогда для элемента i-го звена	dm	i	соответствующий
0		i
ему элемент энергии

dT	1	r i	2 dm ,	(4.3)
	1

i	2		i
	2
где rpi – радиус-вектор этого элемента, р=0, 1, …, n. Из
формулы
	Ai	Di Ai		(4.4)
		Di Ai		(4.4)

следует, что

r i B r i ,		(4.5)
i	i
где Bi Bi (q1 , , qn ) Bi (q)	-	матрица перехода от i-й

системы координат к инерциальной. Следовательно,

(4.6)

dTi

(Bi ri

, Bi ri

)dmi .

Воспользовавшись известным соотношением для векто-

ров a и b

(a, b) = a*b = tr (ab*)

(4.6)

перепишем формулу (4.2) в другом виде:

i* *

(4.7)

dTi

tr(Bi ri

)dmi .

Полная кинетическая энергия i-го звена

(4.8)

dTi

tr(Bi

(

dmi

)Bi ),

где интеграл берется по объему i-го звена. Назовем мат-

рицей инерции i-го звена

	H	i		r i r i*dm ;				(4.9)
		i		i	i	i
					i
тогда
			1			*		(4.10)
Ti		2		tr(Bi	Hi	Bi	).	(4.10)
		2

Теперь заметим, что объект манипулирования представляет собой некоторый груз, жестко связанный с последним (n- м) звеном. Поэтому последнее звено можно рассматривать совместно с грузом и матрицу инерции этого звена Hn формировать, учитывая груз. В результате получаем выражение для кинетической энергии манипулятора с грузом:

			1 n			*		(4.11)
	T			tr(Bi	H i	Bi ).
	T		2 i 1	tr(Bi	H i	Bi ).
			2 i 1
Элементы матриц Hi, i=1, …, n, хорошо известны в меха-
нике. Учитывая, что r i	(xi ,1)*			(xi , xi		, xi	,1)* ,	можем запи-
i		i		1i	2i	3i

сать

	(xi		)2 dm			xi	xi			dm
	1i				i	2i			1i	i
	xi	xi			dm	(xi		)2 dm
H i	1i			2i	i	2i				i
H i	xi	xi			dm	xi	xi			dm
	xi	xi			dm	xi	xi			dm
	1i			3i	i	2i			3i	i
	xi			dm		xi			dm
		1i			i		2i			i

где mi – масса i-го звена;

J i	J i	(xi	)2 dm ,
(2,3)	(3,2)	1i	i

xi	xi			dm	xi	dm
3i			1i	i	1i			i
xi	xi			dm	xi	dm
3i			2i	i	2i			i	,	(4.12)
(xi		)2 dm			xi	dm
3i				i	3i			i
xi			dm		m		i
	3i			i			i
J i				J i	(xi			)2 dm ,
(1,3)				(3,1)			2i			i

J (1,i	2) J (i2,1)	(x3i i	)2 dm (4.13)
			i

– моменты инерции относительно плоскостей (x2i, x3i), (x1i, x3i), (x1i, x2i) соответственно;

J i	J i	xi	xi	dm ,	J i	J i	xi	xi	dm ,
12	21	1i	2i	i	23	32	2i	3i	i

J i	J i	xi	xi	dm	(4.14)
13	31	1i	3i	i

– центробежные моменты.

Заметим, что для систем координат, связанных со звеньями, матрицы Hi, i=1,…,n, могут иметь совершенно произвольный вид, за исключением того, что они будут симметрическими. Если в качестве таких систем координат выбрать системы координат, оси которых являются осями главных эллипсоидов инерции звеньев, то матрицы Hi, i=1,…,n, будут иметь диагональный вид.

П р и м е р 4.1. Рассмотрим i-е звено манипулятора, являющееся однородной трубкой длины li, массы mi с внутренним и внешним радиусами R1i, R2i соответственно (i=1,…,n). Пусть система координат (x1i, x2i, x3i) выбраны так, что если сочленение Pi относится к типу вращение относительно про-

дольной оси звена или поступательное перемещение звена относительно его продольной оси, то ось x3i будет идти по оси i- го звена и

(R 2	R 2	) / 4	0		0		0
1i	2i
	0	(R 2	R 2	) / 4	0		0
H i		1i	2i						mi ; (4.15)
H i	0		0		l 2	/ 3	l		mi ; (4.15)
	0		0		l 2	/ 3	l	i	/ 2
					i			i
	0		0		li	/ 2	1

если сочленение Pi относится к типу, осуществляющее

вращение звена относительно оси, перпендикулярной оси звена, то ось x2i будет идти по оси i-го звена и

(R 2

R 2

) / 4

l 2

/ 3

/ 2

H i

. (4.16)

(R 2

R 2

) / 4

/ 2

Потенциальная энергия П манипулятора с грузом, очевидно, определяется формулой

n
П g( 3 , mi Bi rc,i ),	(4.17)
i 1

где g – ускорение силы тяжести, 3 (0, 0, 1, 0)*, mi –

масса i-го звена, rc, i – радиус-вектор центра масс i-го звена в системе координат, связанной с этим звеном i=1,…,n.

Определим производные Т и П для уравнений (4.1). Так

как

n	Bi	n
	Bi	q j	j
Bi	q j	q j	Bi	q j	(4.18)
j 1	q j	j	1

(здесь матрицы Bi j , как и матрицы Bijl ниже, определены формулами

B j	A1	Aj 1 D j Aj	Aj 1 Ai	, если j i,
B j				(4.19)
i	0,	если с	i;
	0,	если с	i;

A1 Aj

1 D j Aj

1 Dk Ak Ai ,

если

k i,

B jk

A A

A ,

если

, (4.20)

если

и B j

0 для

i ), то

tr(B j

Bl* )q

(4.21)

2 i 1 j ,l 1

i i

k-е уравнение Лагранжа в явном виде имеет вид

tr(B j H B k* )q

tr(B jl H

B k* )q

i k

j 1

i k

j ,l 1

m Bk r

)

1, , n. (4.22)

c,i

i k

Обобщенная

сила,

действующая

k-м

сочленении

( k 1, , n ),

M k

M п,k

M в,k ,

где Mп,k – момент силы или усилие на выходе k-го привода; Mв k – внешний возмущающий момент или усилие, отнесенные к k-й обобщенной координате.

Перегруппировывая слагаемые в формуле (4.10), получим окончательный вид уравнений Лагранжа:

a ji q

, k 1, , n, (4.23)

i 1

j 1 i

где

tr(Bi H

B k* ),

l l

max(i,k )

a ji

tr(B ji

B k* ),

max(

i, j ,k )

					n
a	2k	g(	3	,	m Bk r	),
	2k		3		i i c,i
				i	k

	1, если j i,	(4.24)
ji	2, если j i;i, j, k 1, , n.	(4.24)
ji

Уравнение (4.11) можно более коротко переписать в виде

A(q, )q b(q, q, ) M, (4.25)

где 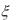- вектор параметров манипулятора и перемещаемого им груза (длины звеньев, масса и моменты инерции звеньев,

масса и моменты инерции груза и т.

д.); A(q,

) - матрица-

функция размерности n

n с элементами

(A)

k,i

1, , n;

(4.26)

b(q, q, ) - вектор-функция размерности n, элементы ко-

торой

a ji q

1, , n; (4.27)

k 2

i 1 j i

при этом второе слагаемое является моментом (усилием) в k-м сочленении, создаваемым весом нагрузки на валу k-го сочленения, от (k+1)-го, (k+2)-го, …, n-го звеньев манипулятора и груза.

Та простота, с которой мы можем находить положение и ориентацию звеньев манипулятора, т. е. вид матрицы Ti, существенно зависит от выбора системы координат звеньев Oi X iYi Zi . Рассмотрим способ построение системы координат,

1 / 41 2 3 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]