Добавил:

mihail1000 Опубликованный материал нарушает ваши авторские права? Сообщите нам.

Вуз:

Воронежский государственный технический университет

Предмет:

[НЕСОРТИРОВАННОЕ]

Файл:

Учебное пособие 800168

.pdf

Скачиваний:

Добавлен:

01.05.2022

Размер:

751.61 Кб

Скачать

☆

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

8.26.		= x y ; y 3z ; x 2z ,	σ: x 2y z 4 0 .
	F
8.27.		= y ; y x ; x z ,	σ: 2x y 2z 2 0 .
	F
8.28.		= 2y ; 3y x ; x 2z ,	σ: 2x y z 4 0 .
	F
8.29.		= 3x y ; 2x y ; y z ,	σ:	2x y z 4 0 .
	F
8.30.		= 2x y ; 2y z ; 2x ,	σ:	x y 3z 3 0 .
	F

Задание № 9. Найти оригинал по заданному изображе-

нию

			2 p 5
9.1.	p 1 p 2			4 p 13 .
			p 1
9.3.	p 2 p 2			p 1 .
		p 5
9.5.	p3 1 .
			p 1
9.7.	p 4 p 2			2 p 5 .
			1
9.9.	p 2 2 p 2 1 .
		p 3
9.11.		p3	8 .
			p 3
9.13.					.
		p 2	6 p 10 2
		p 1
9.15.		p 4	p 2	.

		5 p 1
9.2.		p 1 p 2 2 p 5 .
		2 p 7
	9.4.	p3 2 p 2 5 p .
		p 3
9.6.	p 3 p 2 4 p 5 .
		p 3
9.8.	p 5 p 2 6 p 10 .
		p
9.10.		p 3 p 2 4 .

9.12.	p3	p 6	3 p .
		2 p 2
	p 1
9.14.	p3	8 .
		7 p 1
9.16.	p 2 p 2		2 p 10 .

			3 p 1
9.17.		p3	3 p 2	4 p .
			p 3
9.19.		p 2	4 p 2 9 .
			p 3
	9.21.	p 5 p 2		2 p .
		3 p 5
	9.23.	p 4	9 p 2	.
			p 2
9.25.		p 2	1 p 2 4 .
	9.27.	p 4	1	.
	9.27.	p 4	4 p 2	.
			2 p 4
9.29.					.
9.29.	p 2		2 p 2 2		.

					p
9.18.	p 1 p 2 4 p 5 .
				3 p 5
	9.20.	p 4			4 p 2	.
				2 p 1
9.22.	p3 8 .
					p 3
9.24.							.
				p 2	2 p 5 2
				2 p 3
9.26.			p3		8 .
					4 p 3
9.28.		p3			4 p 2	5 p .
					4 p 5
9.30.			p 2 p 2			4 p 5 .

Задание № 10. Найти решение дифференциального уравнения или системы дифференциальных уравнений, удовлетворяющих начальным условиям, операционным методом.

10.1.	x 4x 8sin 2t					.
	x 0
		3; x		0 1
	x 2x 5 y 1
10.2. y x 2 y 1 .
	x 0 0;		y 0 2
			6e	t
10.3.	x x				.
	x 0
		3; x		0	1

	x 2x 5y
10.4. y x 2 y 2 .
	x 0 2; y 0 0
10.5.		x	4x 8sin 2t				.
10.5.						2	.
	x 0 1; x 0					2
	x x 2 y 1
10.6. y 4x y						.
	x 0 0; y 0 1
				t	2
10.7.		x	x	t				.
	x 0 0; x 0 1
	x x 4 y
10.8. y 2x y 9 .
	x 0 1;			y 0 0
10.9.		x	3x 2x et				.
10.9.							.
	x 0 1; x 0					0
		x x 3y 2
10.10. y x y 1 .
		x 0 0; y 0 1
10.11.		x 2x 3x 2t						.
10.11.		x 0						.
		x 0		1; x 0			1
		x 2x y
10.12. y 3x 4 y						.
		x 0 2; y 0 1

10.13.	x	x x 7e2t						.
10.13.								.
	x 0 1; x 0					4
	x x 4 y
10.14. y 2x y 9 .
	x 0 0; y 0 2
10.15.	x	x 2 cos t						.
10.15.								.
	x 0 0; x 0					1
	x 3x 4 y 1
10.16. y 2x 3y						.
	x 0 0; y 0 2
				2
10.17.	x	x	t	2t				.
	x 0 0; x 0 2
	x x 2 y 1
10.18. y 4x y					.
	x 0 1;		y 0 2
10.19.	x	x cos 3t					.
10.19.					1		.
	x 0 1; x 0				1
	x 3x y
10.20. y 5x 3y 2 .
	x 0 2; y 0 0
10.21.	x	x 6x 2						.
10.21.								.
	x 0 1; x 0					0

	x 3x 4 y 1
10.22. y 2x 3y			.
	x 0 2; y 0 0
10.23.	x 4x	3x et

	x 0 1; x 0 0
	x x 3y 2
10.24. y x y 1
	x 0 1;	y 0 2
10.25.	x 3x	4x 2t

	x 0 1; x 0 1

	x 2x y
10.26. y 3x 4 y			.
	x 0 0; y 0 1
10.27.	x x	x e2t	.

	x 0 1; x 0		2
	x 2x 5 y
10.28. y x 2 y 2 .
	x 0 1;	y 0 1
	x 5x 6x et
10.29.	x 0 1;	x 0 1 .

x 2x 5 y 1

10.30. y x 2 y 1 . x 0 1; y 0 0

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задание № 1. Исследовать сходимость числовых рядов

а)

, б)

(2n)!

n(ln n)2

n 1

n 2

Решение

(1а).

Воспользуемся

признаком

Даламбера.

Имеем

, un 1

(n 1)3

. Применяя признак, вычис-

(2n 2)!

(2n)!

лим

l= lim

un1

lim

(n 1)

3 (2n)!

lim

n 1

=0<1.

(2n

2)!n3

n n

(2n 1)(2n 2)

По признаку Даламбера данный ряд сходится.

Решение (1б).

Введем функцию непрерывного аргумента f(x)=

, за-

x ln 2 x

менив в формуле общего члена ряда

a(n)

целочис-

n ln 2 n

ленную переменную на непрерывную, и исследуем сходимость, используя интегральный признак. Для этого вычислим

lim

d (ln x)

x(ln x)2

(ln x)2

= lim

lim

ln x

ln 2

ln b

ln 2

Из сходимости несобственного интеграла следует сходимость данного ряда.

Задание №2. Найти область сходимости степенного ряда

x n

2n n2

n 1

Решение. Вычислим

l = lim

un 1

lim

n 1 n2 2n

2n 1 (n 1)2

x n

По признаку Даламбера ряд сходится при l < 1, отсюда 2x < 1, |x| < 2 или -2<x<2. Следовательно, ряд абсолютно схо-

дится в интервале при -2<x<2. Граничные точки подлежат дополнительному исследованию. При x =2 и x = -2 из данного

					1

ряда	получаем соответственно числовые ряды				n 2 и
ряда	получаем соответственно числовые ряды			n 1	n 2 и
				n 1
	( 1)n
		.	Из интегрального признака сходимости следует,
n 1	n2	.
	n2

что эти ряды абсолютно сходятся, поэтому областью сходимости данного ряда является отрезок [-2, 2].

Задание № 3. Вычислить определенный интеграл

cos2x dx с точностью до 0,001, разложив подынтеграль-

ную функцию в ряд.

Решение. Пользуясь рядом Маклорена для cos x , заменяя в нем x на 2x , имеем

								2x				4x 2			8x3			16 x 4
			cos 2x			= 1 –								–						– ... .
			cos 2x			= 1 –		2!		+	4!			–		6!	+		8!	– ... .
Интегрируя в указанных пределах, получим
	1								x 2				x3			x 4			x5			1
	1

		cos		2x dx = x																	...		=
		cos		2x dx = x					2				6 3			90 4			2520 5		...	0	=
	0


1	1		1		1		1	....
1	2					12600		....
	2	18		360		12600

Пятый член этого знакочередующегося сходящегося ряда меньше 0,001. Поэтому для вычисления искомого приближенного значения интеграла достаточно взять четыре первых члена ряда:

				1
						cos			2x dx =
		1		0	1			1
1		1			1			1		1 0,5 0,056 0,003 0,559.
1										1 0,5 0,056 0,003 0,559.
		2			18		360
			Задание						№		4. Изменить порядок интегрирования
											3 x
1	x3							3			2
dx f x, y dy dx f x, y dy .
0		0						1			0

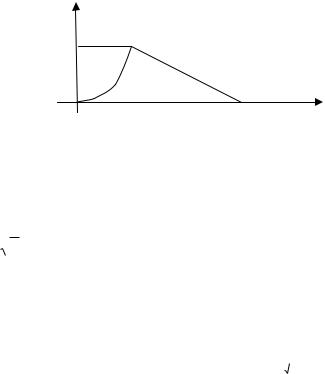
Решение. При объединении областей интегрирования, соответствующих двум двукратным интегралам, образуется область интегрирования, представляемая криволинейным треугольником ОАВ. Эта область ограничена линиями y x3 ,

y	3 x	и y 0 .
y	2	и y 0 .
	2
		26

1	A
		B


O	1	3	x

Рис. 1

Поскольку при изменении порядка интегрирования область описывается с помощью системы неравенств

0 y 1,

3 y x 3 2 y,

то это позволяет расставить пределы интегрирования в соответствии с данной системой неравенств:

			3 x
1	x3	3	2	1	3 2 y
dx f x, y dy dx				f x, y dy dy		f x, y dx
0	0	1	0	0	3		y
Задание №5. Вычислить объем тела, ограниченного по-
верхностями	z 1,	z 2 x2 ,		y x2 ,		y 1 2x2 . Сде-

лать чертеж его проекции на плоскость хОу.

Решение. В прямоугольной декартовой системе координат двукратный интеграл позволяет вычислять объем цилиндроида, тела, имеющего боковую цилиндрическую поверхность. Если область цилиндроида может быть определена системой неравенств

		a x b,
		y1 (x) y y2 (x),
		y1 (x) y y2 (x),
z (x, y) z z			2	(x, y),
	1		2

то объем тела V находится по формуле

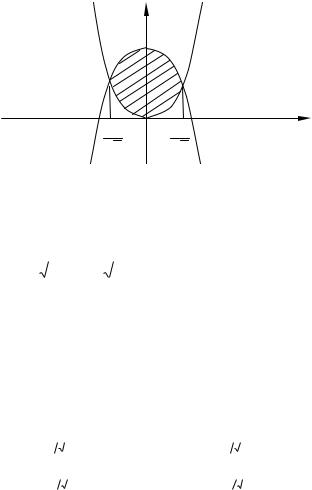
b y2 (x)

V dx z2 (x, y) z1 (x, y) dy . a y1(x)

Для определения пределов интегрирования сделаем чертеж проекции тела на плоскость xOy. Проекция боковой цилиндрической поверхности образует границу области D.

y=x2 y=1-2x2

1 O

3 3

Рис. 2

Для переменной внешнего интегрирования x пределы определяются наибольшим и наименьшим значениями в области

D, т.е.	1	x	1	. Переменная внутреннего интегрирова-


3		3

ния y, являясь функцией переменной x, для каждого значения x

меняется от значения, задаваемого нижней кривой			y x2 , до
значения,	задаваемого верхней кривой.	Следовательно,
x2 y 1 2x2 . Поскольку цилиндроид		снизу	ограничен
плоскостью	z 1, а сверху поверхностью z	2 x2 , то пере-

менная z удовлетворяет двойному неравенству 1 z 2 x2 . Поэтому

1 2 x2

1 3

2 x2 1

(1 x2 )dy

1 3

<<< < Предыдущая 1 23 / 43 4 > Следующая >>>

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

#
01.05.2022726.95 Кб1Учебное пособие 800163.pdf
#
01.05.2022732.76 Кб1Учебное пособие 800164.pdf
#
01.05.2022736.38 Кб2Учебное пособие 800165.pdf
#
01.05.2022736.39 Кб2Учебное пособие 800166.pdf
#
01.05.2022738.99 Кб3Учебное пособие 800167.pdf
#
01.05.2022751.61 Кб1Учебное пособие 800168.pdf
#
01.05.2022758.08 Кб2Учебное пособие 800169.pdf
#
01.05.2022259.96 Кб7Учебное пособие 80017.pdf
#
01.05.2022759.69 Кб5Учебное пособие 800170.pdf
#
01.05.2022761.56 Кб12Учебное пособие 800171.pdf
#
01.05.2022782.64 Кб3Учебное пособие 800172.pdf