3.2. Кодирование в дискретных каналах

В этой и следующей главах будет рассматриваться кодирование при передаче сообщений по каналам связи, подверженным воздействию шума. В любом реальном канале связи, который используется для передачи сообщений, всегда в той или иной степени действует шум. В результате воздействия шума на приемной стороне никогда не может быть вынесено абсолютно достоверное решение о том, какое сообщение передавалось по каналу. Наличие такой неопределенности приводит к существованию ненулевой вероятности ошибочной передачи сообщения. Если не принимать соответствующих мер для защиты передаваемых сообщений, то эта вероятность может оказаться весьма большой.

Защита сообщений от влияния шума канала реализуется с помощью специальных методов кодирования. Легко понять, что одним из возможных методов защиты является увеличение энергии, затрачиваемой на передачу каждого сообщения, например, с помощью многократного повторения передачи одного и того же сообщения. Однако при таком методе защиты время передачи одного сообщения становится весьма большим и, следовательно, скорость передачи — весьма низкой. Возможен и другой метод увеличения энергии, основанный на увеличении мощности передатчика. Однако зачастую на практике мощность передатчика не может быть увеличена в силу различных технических ограничений.

Повторение сообщений является тривиальным методом кодирования. Оказывается, что имеются нетривиальные методы кодирования, которые позволяют осуществлять передачу сообщений со сколь угодно высокой достоверностью и относительно высокой скоростью. Основной задачей, которую мы будем решать в этой и следующей главе, является определение по заданной статистической модели канала величины наибольшей скорости, при которой возможна передача сообщений с произвольно малой вероятностью ошибки.

1. Классификация каналов связи

На рис. 3.1 приведена структурная схема системы связи. Всякая система связи использует некоторый канал связи. Физически канал представляет собой среду, в которой распространяются сигналы, соответствующие передаваемым сообщениям. Например, это меняющиеся во времени значения напряжения или тока, если канал образован парой проводов, или меняющаяся во времени напряженность электромагнитного поля в случае радиоканалов. Однако часто в канал включают не только физическую среду, но и некоторые устройства, сопряженные с входом и выходом физического канала. Например, это могут быть антенные устройства, выходные цепи передатчиков и входные цепи приемников. В зависимости от этого получаются различные модели реальных каналов связи.

Шум, действующий в канале, имеет такую же физическую природу, что и сигналы, и, как обычно предполагается в статистической теории связи, никогда не известен точно наблюдателю, находящемуся на приемной стороне системы связи. Поэтому наблюдатель всегда находится перед проблемой определения того, что же было передано по каналу.

Источник

Кодер

источ-

ника

Шум

Источ-ник

Кодер

канала

Моду-лятор

Канал

Получатель

Декодер

источ-

ника

Полу-чатель

Демо-дулятор

Декодер

канала

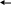
Рис. 3.1. Структурная схема система связи

Здесь мы будем предполагать, что кодер источника выбран достаточно хорошо, поэтому можно считать, что символы, появляющиеся на его выходе, независимы и равновероятны. Таким образом, пару «источник — кодер источника» можно рассматривать как новый источник дискретных сообщений. Аналогично пару «декодер источника - получатель» мы будем рассматривать как получателя сообщений в системе передачи. Роль остальных блоков системы связи сводится к тому, что обеспечить максимально надежную передачу последовательности независимых равновероятных символов. Основную роль в решении этой задачи играет пара «кодер —декодер» канала.

Роль пары «модулятор — демодулятор» можно пояснить следующим образом. Предположим, что задано множество символов на выходе кодера канала. Эти символы могут передаваться с помощью различных сигналов. Например, если символов всего два, то они могут быть переданы либо двумя значениями амплитуды несущих колебаний, либо двумя значениями частоты, либо двумя значениями длительности колебаний при фиксированной частоте и амплитуде и т. д.

Форма сигналов влияет на результирующее действие шумов. Например, при одинаковом источнике шума частота ошибок при использовании второго метода передачи может быть меньшей, чем при использовании первого.

Устройство, сопоставляющее каждому символу или группе символов на выходе кодера соответствующий входной сигнал канала, называется модулятором. Устройство, выполняющее обратное преобразование, называется демодулятором. Задачей конструктора системы связи является построение таких пар «кодер — декодер», «модулятор — демодулятор», которые наиболее эффективно уменьшают влияние шумов.

Для осуществления этой задачи необходимо совместное проектирование указанных пар. Однако довольно часто встречается ситуация, когда проектировщик системы не имеет возможности выбирать способ модуляции и демодуляции. Такая ситуация имеет место, например, когда пользователю предоставляется канал вместе с модулятором и демодулятором, а возможно выбирать только метод кодирования и декодирования. В этом случае каналом для проектировщика системы связи является та часть на рис. 3.2.1., которая находится между выходом кодера канала и входом декодера канала. Такой канал называют дискретным. Действие шума проявляется в том, что символ на выходе кодера может не совпадать с соответствующим ему символом на входе декодера.

Общее проектирование кодера и модулятора, а также декодера и демодулятора является весьма сложной задачей. В этом разделе мы всегда будем предполагать, что модулятор—демодулятор и, следовательно, система используемых сигналов выбрана, а задача состоит в выборе пары кодер —декодер.

Для теории информации физическая природа сигналов и шумов является несущественной. Так же, как и при кодировании источников, мы будем рассматривать сигналы на входе и выходе канала как элементы некоторых абстрактных множеств (алфавитов). В предыдущем изложении мы различали дискретные и непрерывные источники в зависимости от выбора множества сообщений. Аналогичная классификация имеет место и для каналов.

Канал называют дискретным по входу (выходу), если множество входных (выходных) сигналов конечно.

Иногда дискретным называют такой канал, в котором эти множества, или одно из них, счетно. В настоящем изложении каналы со счетными бесконечными алфавитами не встречаются.

Канал называют непрерывным по входу (выходу), если множество входных (выходных) сигналов несчетно.

Канал называют каналом, дискретным по входу и непрерывным по выходу (полунепрерывным), если множество входных сигналов конечно, а множество выходных сигналов несчетно.

Обычно множество входных сигналов канала будет обозначаться через X, а некоторый элемент этого множества — через х. Аналогичные обозначения Y и у используются для обозначения выходных сигналов канала.

Говоря о непрерывных или полунепрерывных каналах, мы в дальнейшем будем предполагать, что их вероятностное описание может быть дано в терминах функций плотностей вероятностей. Такое ограничение не является существенным, оно принято только в целях упрощения изложения.

Канал называют каналом с дискретным временем, если сигналы на его входе и выходе представляют собой конечные или бесконечные последовательности с элементами из алфавитов X и Y соответственно. Дискретный по входу и выходу канал с дискретным временем мы будем называть дискретным каналом.

Канал называют каналом с непрерывным временем, если сигналы на его входе и выходе представляют собой действительные функции времени. Непрерывный по входу и выходу канал с непрерывным временем мы будем называть непрерывным каналом.

В этом резделе рассматриваются только дискретные каналы. Непрерывные каналы (с дискретным и непрерывным временем) будут рассмотрены в следующем разделе.

Для полного задания канала необходимо задать статистическое описание процесса передачи. Как уже отмечалось, наличие шума может привести к тому, что один и тот же входной сигнал канала может перейти в различные выходные сигналы. С математической точки зрения такие переходы могут описываться с помощью распределений вероятностей. В случае дискретного канала переходы входных сигналов в выходные задаются условными вероятностями р (у|х), хX, у Y, получения на выходе сигнала у, если на входе был сигнал х.

В дальнейшем X и Y будут рассматриваться как множества сигналов на входе и выходе канала, которые появляются в некоторый фиксированный момент времени. Поэтому условные вероятности {р(у|х)} будут описывать только процесс однократной передачи (передачи одного сигнала) в этот фиксированный момент времени. Однако по каналу никогда не передается один-единственный сигнал, а передается, как правило, достаточно длинная последовательность сигналов. Поэтому задание только одномерных условных вероятностей или условных плотностей вероятностей в общем случае не описывает процесс передачи полностью.

Мы будем говорить, что дискретный канал задан, если для любых целых чисел n и j и любых последовательностей

(x^(j), x^(j+1),..., х^(n+j1)) (y^(j), y^(j+1),..., y^(n+j1))

с элементами из дискретных множеств X и Y соответственно заданы условные (или переходные) вероятности р (y^(j), y^(j+1),..., …,y^(n+j1) | x^(j), x^(j+1),..., х^(n+j1)) получения на выходе канала последовательности (y^(j), y^(j+1),..., y^(n+j1)), если на входе канала была последовательность (x^(j), x^(j+1),..., х^(n+j1)).

Дискретный канал называют каналом без памяти, если для любых n и j, а также для любых последовательностей (x^(j), x^(j+1),..., х^(n+j1)) и (y^(j), y^(j+1),..., y^(n+j1)) имеют место равенства

(3.35)

где p_i (y|x) —вероятность для момента времени i получения на выходе канала сигнала у, если на входе был сигнал х.

Название «без памяти» подчеркивает тот факт, что если выполняются соотношения (3.35), то при очередной передаче канал как бы не помнит результатов предыдущих передач.

Будем говорить, что дискретный канал без памяти удовлетворяет условию стационарности, если для любых i, j, х X, у Y

p_j (y | x)= p_i (y | x) (3.36)

Другими словами, статистические характеристики процесса передачи последовательностей сигналов по стационарному каналу без памяти не зависят от момента начала передачи и сохраняются постоянными на протяжении всего времени передачи.

Из определения следует, что для задания дискретного канала без памяти, удовлетворяющего условию стационарности, достаточно задать лишь одномерные переходные вероятности. В дальнейшем мы всегда будем предполагать, если это не оговорено особо, что дискретные каналы без памяти удовлетворяют условию стационарности. При этом дискретный канал без памяти мы иногда будем обозначать как {XY, р (у|х)}, где X, Y — входной и выходной алфавиты и р (у|х), х X, у Y, — переходные вероятности канала.

Ниже мы будем всюду предполагать, что зафиксирован момент времени j, в который начинается передача по каналу связи. Для простоты будем полагать j = 1. Из приведенных определений следует, что в общем случае для задания дискретного канала, по которому сообщения передаются, начиная с момента j = 1, необходимо задать переходные вероятности р (у | х) для всех n = 1, 2, … и всех последовательностей x  (x⁽¹⁾,..., х⁽ⁿ⁾)Xⁿ и y  (y⁽¹⁾,..., y⁽ⁿ⁾)Yⁿ. Мы будем предполагать, что переходные вероятности удовлетворяют следующим условиям согласованности:

n=1, 2,…, k=1,…,n - 1

Каналы, удовлетворяющие условиям согласованности, называются каналами без предвосхищения. В таких каналах вероятность появления выходного сигнала в некоторый момент времени не зависит от сигналов, которые появятся на входе канала в последующие моменты времени.

Отметим, что распределение вероятностей на входе канала не входит в описание канала, поскольку входное распределение определяется устройствами на входе канала (источником, кодером источника и кодером канала), но не самим каналом. Однако, если некоторое входное распределение, скажем р(х), задано, то оно вместе с условными вероятностями р(у|х) задает совместное распределение вероятностей на парах (х, у) ХⁿУⁿ

p (x, y)=p (y | x) p (x) (3.37)

и распределение вероятностей на выходных последовательностях канала

(3.38)

3.2.2. Постановка задачи кодирования в дискретном канале

Назначение кодера и декодера канала состоит в том, чтобы уменьшить влияние шумов в канале и обеспечить надежную связь между источником и получателем сообщений. В следующем примере рассматривается один из методов повышения надежности связи.

Пример 3.1. Пусть множества входных и выходных сигналов дискретного канала без памяти состоят из двух элементов {0, 1} и пусть р (0|1) = р (1|0) = р. Такой канал называется двоичным симметричным и полностью определяется заданием величины р. Действительно, если х, у— последовательности длины n из нулей и единиц на входе и выходе канала, то

Где t — количество позиций, на которых последовательности х и у различаются, другими словами, t — количество ошибок при передаче х и получении у.

Предположим, что р < 0,5 и требуется передать одно из двух сообщений z₁ или z₂. Можно было бы закодировать эти сообщения так: z₁0, z₂1. Однако при этом вероятность неправильного приема сообщения равнялась бы р.

Рассмотрим другой метод кодирования (передачу с помощью повторений): если надо передать z₁, то по каналу передается последовательность из n нулей, если же надо передать z₂, то по каналу передается последовательность из n единиц. Приемник работает по следующему правилу: если в принятой последовательности количество нулей больше количества единиц, считается, что передавалось z₁, в противном случае считается, что передавалось z₂.

Очевидно, что ошибка декодирования возникает всякий раз, когда при передаче последовательности длины n число ошибок t превосходит или равно n/2. Так как в рассматриваемом канале вероятность ошибочного приема сигнала равна р и не зависит от того, какой сигнал, 0 или 1, передавался, то вероятность  неправильного приема сообщения можно определить следующим образом:

(3.39)

Так как математическое ожидание числа ошибок в последовательности длины n равно nр < n/2, то в силу закона больших чисел  стремится к нулю при возрастании n.

Таким образом, мы видим, что вероятность неправильной передачи сообщений по каналу может быть сделана сколь угодно малой, если это сообщение передается посредством достаточно большого числа повторений одного и того же входного сигнала. Время передачи при таком методе кодирования пропорционально числу повторений. Поэтому, чтобы вероятность неправильного приема была достаточно малой, необходимо иметь достаточно большое время передачи. При этом скорость передачи, т. е. количество информации, передаваемое в единицу времени, будет стремиться к нулю, так как за все время передачи будет передано одно из двух сообщений или не более 1 бита информации.

Произвольно малая вероятность ошибки может быть также достигнута и при скоростях передачи, отличных от нуля, за счет усложнения методов кодирования и соответственно декодирования.

Кодом с длиной n и объемом М для канала называется множество из М пар {u₁, A₁; u₂, A₂;...; u_M, A_M} где u_iXⁿ; i=1,...,М — последовательности длины n, образованные входными сигналами канала и называемые кодовыми словами (u_iu_j при i  j), и A_i  Yⁿ, i = 1, 2, ... ..., М, — решающие области, образованные выходными последовательностями канала, причем при i  j множества А_i и А_j.

Если задан код, то тем самым задано как множество кодовых слов, так и правило, по которому приемник принимает решение о переданном кодовом слове: если на выходе канала появляется последовательность у и у A_i то приемник принимает решение о том, что передавалось слово u_i.

Скоростью кода (или скоростью передачи) называется величина

(3.40)

где М — объем и n — длина кода.

Из этого определения следует, что скорость кода представляет собой максимальное количество информации, которое может быть передано с помощью одного сигнала (или символа), так как log M есть максимальное количество информации, которое может быть передано с помощью одного кодового слова. Это количество информации действительно передается, когда кодовые слова имеют одинаковые вероятности появления. Скорость измеряется в битах на символ. Если скорость кода равна R бит/символ, то с помощью такого кода можно передавать nR двоичных единиц информации за время передачи одного кодового слова (за n единиц времени).

Очевидно, что число кодовых слов не может превышать общего числа последовательностей длины n, образованных символами входного алфавита (входными сигналами), канала. Для дискретных каналов это число равно Lⁿ, где L — число элементов множества входных сигналов. Следовательно, в случае дискретных каналов R  log L.

Следует отметить разницу в определениях скорости кода канала и скорости кода источника. В случае кода источника скорость определяется как отношение логарифма числа кодовых слов к длине отрезков кодируемых сообщений. В случае кода канала скорость определяется как отношение того же числа к длине кодовых слов (к длине кодирующих последовательностей).

Очевидно, что код длины n, имеющий скорость R, имеет объем М = 2^nR. Такой код в дальнейшем будем обозначать символом G(n, R).

Пример 3.2. Предположим, что двоичный источник без памяти имеет энтропию Н(X) < 1. Как было показано ранее, при кодировании сообщений такого источника можно достичь скорости, близкой к Н(X). Это означает, что при появлении на входе кодера источника n двоичных символов, где n достаточно велико, на выходе кодера появляется примерно nН(X) двоичных символов, что меньше, чем n. Если теперь рассматривать последовательности длины nН(X) как входные сообщения для кодера двоичного канала, осуществляющего кодирование со скоростью R < 1, то длина кодовых слов будет равна , что больше, чем nН(X). Таким образом, кодирование источника понижает длину последовательностей сообщений, а кодирование в канале ее увеличивает. В связи с этим кодирование источника иногда называют устранением избыточности, а кодирование в канале — введением избыточности. Последовательное применение этих двух операций в большинстве случаев увеличивает эффективность передачи по сравнению с непосредственной передачей сообщений источника без какого-либо кодирования.

Если заданы некоторый канал и код, то мы можем определить вероятность ошибки декодирования данного кода при передаче по данному каналу. Пусть передается слово u_i некоторого фиксированного кода G(n,R), тогда ошибка декодирования возникает в случае, когда последовательность на выходе канала не принадлежит решающей области A_i. Обозначая через _i вероятность ошибки декодирования при условии передачи слова u_i ,получим

(3.41)

где — дополнение к множеству A_i.

В качестве количественной меры надежности передачи с помощью кода G(n,R) мы будем использовать две величины. Первая — максимальная вероятность ошибки

  max {₁, ..., _M } (3.42)

Вторая — средняя вероятность ошибки

(3.43)

где р (u_i) — вероятность передачи i-го кодового слова.

Так как распределение вероятностей р(u_i) характеризует источник сообщений и никак не связано ни с каналом, ни с кодом, то средняя вероятность ошибки декодирования часто определяется следующим образом:

(3.44)

Выражение (3.44) совпадает с (3.43) в случае оптимального кодирования источника, когда р (u_i)= l/M, i = 1, ..., М.

Пропускной способностью канала с дискретным временем называется максимальное число С такое, что для любого сколь угодно малого , >0, и для любого R, R<С, существует код G(n,R) такой, что максимальная вероятность ошибки удовлетворяет неравенству

< (3.45)

С — это верхняя грань скоростей кодов, для которых выполняется (3.45), поэтому передача с произвольно малой вероятностью ошибки при скоростях R>С невозможна и, следовательно, для любого R>С существует положительное число  ' такое, что  ' для любого n и любого кода G (n, R).

Для того чтобы доказать, что некоторое число С является пропускной способностью канала, необходимо доказать два утверждения:

1) при любом R < С и любом положительном  существует код длины n, скорость которого равна R и максимальная вероятность ошибки удовлетворяет неравенству < (прямая теорема кодирования);

2) для всякого R > С найдется положительное число <' такое, что <' для любого п и любого кода G (n, R) (обратная теорема кодирования).

Пропускная способность канала была определена относительно максимальной вероятности ошибки . Очевидно, что, если для некоторого кода максимальная вероятность ошибки не превосходит, то и средняя вероятность ошибки для этого кода также не превосходит . Следующая лемма устанавливает, что в определенном смысле верно и обратное утверждение. Поэтому пропускную способность можно определять как максимальную скорость, при которой средняя вероятность ошибки не превосходит .

Л е м м а Пусть существует код объема М с вероятностью ошибки К, определенной соотношением (3.44), тогда существует код объема М/2, максимальная вероятность ошибки которого удовлетворяет неравенству  2.

Предположим, что в коде объема М кодовые слова u₁,..., u_M упорядочены по невозрастанию вероятности ошибки, т. е. _i _j при i < j. Имеет место следующая цепочка неравенств:

(3.46)

В силу упорядоченности вероятностей ошибок из (3.46) вытекает, что

_j  _M/2  2 (3.47)

для всех j > М/2. Тогда код объема М/2, образованный словами u_M/2+1,..., u_M, имеет максимальную вероятность ошибки, не превышающую 2. Лемма доказана.

Из леммы следует, что, если при любом R'<С существует код G (n, R') такой, что

 < / 2 (3.48)

где  — произвольное положительное число, то при любом R < С существует код G (n, R), для которого < .

Действительно, скорость кода, построенного в доказательстве леммы, равна R=R'—1/n. Поэтому для любого R<С найдется такое, быть может большое, значение n, что R'<С и, следовательно, существует код, для средней вероятности ошибки которого выполняется неравенство (3.48). По лемме подкод объема М/2 этого кода имеет максимальную вероятность ошибки  <  и скорость R.

3.2.3. Неравенство Фано

В этом параграфе будет рассмотрено основное неравенство, с помощью которого доказываются обратные теоремы кодирования для различных каналов.

Пусть задан дискретный ансамбль {UW, р (u, w}, где V={u₁, u₂,…, u_M}, W={w₁, w₂, ..., w_L}. Обозначим через Е событие, состоящее в появлении пары (u_i, w_j), i  j. Это событие будем называть «ошибкой». Положим

(3.49)

(3.50)

где

Величину _j будем называть условной вероятностью ошибки при фиксированном w_j  W, а величину  — средней вероятностью ошибки.

Рассмотрим множество Е = {Е, }, состоящее из двух событий Е и , где — событие, дополнительное к Е, оно наступает при появлении любой пары (u_i, w_j), для которой i=j. На множестве Е для каждого w_jW определено условное распределение вероятностей {_j, 1—_j}. Это распределение совместно с безусловным распределением р (w_j), j = 1, ...,L, задает ансамбль ЕW, для которого

H (E | w_j )   _j log _j  (1-_j ) log (1- _j ) = h (_j) (3.51)

где h (р) = —р log р — (1 — р) log (1 — р), и

(3.52)

Безусловное распределение вероятностей на Е есть {, 1—}. При этом

H (E) = h () (3.53)

В следующей теореме устанавливается связь между условной энтропией H (U|W) и вероятностью ошибки .

Т е о р е м а (неравенство Фано). Для любого дискретного ансамбля {UW, p (u, w)}, |U| = M, справедливо неравенство

H (U | W)  h () +  log M (3.54)

Рассмотрим условную энтропию H(U|w_j). При j М имеем

H (U|w_j) log p(u_i, w_j)= - p(u_j|w_j)log p(u_j|w_j) –

- [1- p(u_j|w_j)]log[1 - p(u_j|w_j)] log p(u_i|w_j)+

+ [1- p(u_j|w_j)]log[1 - p(u_j|w_j)]=H(E|w_j)=

= (3.55)

где последнее равенство следует из (3.49) и (3.51). Из соотношения (3.49) следует также, что

(3.56)

Поэтому второе слагаемое в последнем выражении в (3.55) представляет умноженную, на _j энтропию ансамбля, состоящего из (М—1) сообщений, вероятности которых указаны как слагаемые в сумме (3.3.8). Если эту энтропию оценить сверху величиной log M, то

H (U | w_j)  H (E | w_j) +  _j log M= h( _j)+  _j log M (3.57)

При j > М (такое j найдется, если L > М) имеем

H (U|w_j) log p(u_i| w_j )  log M (3.58)

Так как при j > М всегда происходит ошибка, то при таких значениях j_j = 1 и H(E |w_j) =h (_j) = 0. Следовательно, из (3.58) вытекает, что неравенство (3.57) имеет место при всех j= 1, ..., L.

Усредним обе части неравенства (3.57) по ансамблю W. Для этого умножим правую и левую части неравенства на р(w_j) и просуммируем по всем j. В результате получим, что

H (U | W)  H (E | W) +  log M (3.59)

Поскольку условная энтропия H(E|W) не превосходит безусловную Н(Е)=h(), то из (3.59) следует неравенство (3.54). Теорема доказана.

Рассмотрим, как неравенство Фано может применяться для оценки вероятности ошибки декодирования в дискретном канале связи. Пусть задан дискретный канал, т. е. заданы множества входных X и выходных Y сигналов, а также при всех n = 1, 2, ... заданы условные вероятности р(у|х), уУⁿ, хXⁿ. Предположим, что для передачи по каналу используется код G (n, R) = — {u₁, A₁; u₂, A₂;...; u_M, A_M } длины n и объема М = 2^nR.

Обозначим через W множество решений {w₁, …, w_M, w_M+1}, которые принимает приемник о передаваемых кодовых словах. Решение есть w_j, j  M+1, если выходная последовательность канала принадлежит области A_j, решение есть w_M+1, если выходная последовательность канала не принадлежит ни одной решающей области A_j, j= 1, ..., М. Пусть U = {u₁,…, u_M+1}— множество кодовых слов и р(u_i) — вероятность появления слова u_i на входе канала. Тем самым определен ансамбль {UW, p(u,w)}, элементами которого являются пары (u, w) — (переданное слово, решение), а распределение вероятностей

р (u_i, w_j) = p (u_i) p ( w_j | u_i), i=1,...,M, j=1,..., M+1.

где

При этом величина _j представляет собой условную вероятность ошибки декодирования для кода G (n, R) при условии, что в результате декодирования вынесено решение w_j  W, а величина  (см. (3.50)) представляет собой среднюю вероятность ошибки декодирования. Эта средняя вероятность ошибки может быть вычислена также по формуле :

Энтропия H (U | W) в рассматриваемом случае представляет собой среднюю условную информацию ансамбля кодовых слов при фиксированном множестве решений. Величину Н(U|W) иногда называют ненадежностью передачи с помощью кода G(n,R). Она характеризует количество информации, потерянное при передаче из-за шума в канале. Неравенство Фано (3.54) устанавливает связь между ненадежностью передачи и средней вероятностью ошибки декодирования для кода G (n, R).

Неравенство Фано можно интерпретировать следующим образом. Для того чтобы наблюдатель, находящийся в декодере, мог точно установить переданное сообщение, он, во-первых, должен знать, допускает или не допускает ошибку декодер. Среднее количество информации, необходимое для этого, равно h(). Если наблюдатель знает, что при декодировании произошла ошибка, то ему необходимо дополнительно установить, какое из оставшихся М—1 кодовых слов было действительно передано. Среднее количество информации, необходимое для этого, не превосходит log M. Так как такая необходимость возникает с вероятностью , то среднее количество дополнительной информации не превосходит  log M. Неравенство (3.3.6) обосновывает тот интуитивно ясный факт, что потеря информации в канале из-за действия шумов, т. е. величина H(U|W), не превосходит величины h()+ log M, которая является верхней оценкой количества информации, необходимого для точного установления переданного сообщения.

Правая часть неравенства Фано является функцией только от ; обозначим ее через  ():

(3.60)

Заметим, что  ()  0, причем равенство имеет место только при  = 0. Функция  () является непрерывной на интервале [0, 1]. Беря производную по , можно убедиться в том, что она монотонно возрастает, если 0   < М/М + 1, убывает, если М/М+1<1, и имеет максимум в точке М/М + 1. График функции  () изображен на рис. 3.2

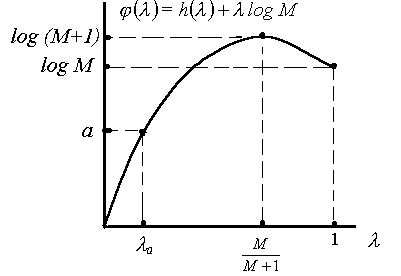
Рис.3.2. График функции  ()

Пусть а — некоторое положительное число, меньшее или равное log M, и _a — наименьшее решение уравнения  () = а. Нетрудно видеть, что следующие два неравенства

(3.61)

равносильны, т. е, первое влечет второе и наоборот.

3.3. Общая обратная теорема кодирования для дискретных каналов

Теперь мы используем неравенство Фано для доказательства обратной теоремы кодирования для широкого класса дискретных каналов.

Рассмотрим некоторый дискретный канал. Пусть задано распределение вероятностей р(х) на входных последовательностях канала хХⁿ. Это распределение совместно с условными вероятностями, посредством которых задается канал определяет ансамбль {XⁿYⁿ, р(у|х) р(х)}. Пусть I(Хⁿ; Yⁿ) — средняя взаимная информация между последовательностями длины n на входе и выходе канала

(3.62)

где

(3.63)

Обозначим через С^* максимальное значение средней взаимной информации в единицу времени между входом и выходом канала

(3.64)

где верхняя грань берется по всем n и всевозможным распределениям р(х), хХⁿ, на входных последовательностях длины n. Мы будем называть этот максимум информационной емкостью дискретного канала.

Точная верхняя грань sup f(х), х X, где f (х) — некоторая функция на X, есть наименьшее число f₀, такое, что f₀  f(х) для каждого х  X. Если в множестве X существует такой элемент х₀, для которого f₀ = f (x₀), то говорят, что верхняя грань достигается на X, и пишут f (x₀) = max f (х), хX. Если X — конечное множество, то верхняя грань всегда достигается. В этом случае всегда sup f (х) = max f (х). Если X — бесконечное множество, то верхняя грань может не достигаться ни на одном элементе из X. Например, если X — множество натуральных чисел и f (х) = 1- , то sup f (х) = 1, но f (х)  1 ни для одного элемента из X. Заметим также, что верхняя грань достигается, если X — замкнутое множество и функция f (x) непрерывна.

Т е о р е м а (обратная теорема кодирования для дискретных каналов). Пусть С^* — информационная емкость дискретного канала и R = С^* +  где  — произвольное положительное число. Тогда существует положительное число , зависящее от R, такое, что для всякого кода G (n, R)

   (3.65)

Зафиксируем некоторое n и рассмотрим код G (n, R) с М = 2^nR кодовыми словами { u₁,…, u_M}. Зададим распределение вероятностей на Хⁿ следующим образом. Положим

(3.66)

Пусть I(Xⁿ; Yⁿ) — средняя взаимная информация между входом и выходом канала, вычисленная для распределения вероятностей (3.4.5). Тогда I(Хⁿ; Yⁿ) = I(U; Yⁿ), где U — ансамбль слов рассматриваемого кода, и из определения информационной емкости следует, что

nС^*  I (Xⁿ; Yⁿ) = I (U; Yⁿ) (3.67)

Пусть W — ансамбль решений. Этот ансамбль можно рассматривать как результат отображения ансамбля Yⁿ всех последовательностей на выходе канала в множество решений. Это отображение задается посредством набора решающих областей A₁,..., A_M. Каждая последовательность y Yⁿ однозначно определяет решение w  W по следующему правилу:

(3.68)

Поскольку информация не возрастает в результате преобразований, то

I (U; Yⁿ)  I (U; W) (3.69)

Так как H (U | W) = Н (U) — I (U; W) и согласно (3.66) H(U)=logМ, то используя неравенство (3.67), получим, что

H (U | W)=log M – I (U;W)  log M – nС^* (3.70)

или

H (U | W)  n(R – С^*) = n (3.71)

Теперь можно воспользоваться неравенством Фано, которое, как было показано выше, выполняется для любого кода и для любого распределения вероятностей р (х) на кодовых словах и, в частности, для кода G (n, R) и распределения вероятностей (3.66). Обозначим через _0n наименьший корень уравнения

h ()+ log M= n (3.72)

Тогда из неравенства Фано и неравенства (3.4.71) следует, что средняя вероятность ошибки , для кода G(n,R) удовлетворяет неравенству   _0n. Легко увидеть, что _0n стремится к  /R при n. Из свойств функции  () (см. предыдущий параграф) следует, что при М  1 число _0n остается положительным при всех п и _0n  ₀₁ > 0. Полагая ₀₁ = , получим, что    для любого кода G (п, R). Теорема доказана.

Цель дальнейшего изложения состоит в том, чтобы показать, что для широкого класса каналов информационная емкость и, пропускная способность совпадают. Для этого нужно доказать прямую теорему кодирования, в которой утверждается существование кода со скоростью R < С^*, обеспечивающего сколь угодно малую заданную наперед вероятность ошибки. Путь, которому мы следуем, состоит в том, что вначале вычисляются величины информационных емкостей ряда достаточно простых каналов, а затем для каждого из рассмотренных каналов доказываются индивидуальные прямые теоремы кодирования. Доказательства для простых каналов обладают необходимой прозрачностью и позволяют наиболее выпукло показать фундаментальные идеи теории информации.

3.4. Информационные пределы избыточности. Принципы помехоустойчивого кодирования

Кодирование, с помощью которого можно устранять ошибки обусловленные наличием шума в канале называется помехоустойчивым. Коды способные исправлять и обнаруживать ошибки называется помехоустойчивым кодом. К сожалению основная теорема кодирования Шеннона не конструктивна, она не указывает способ построения конкретного оптимального помехоустойчивого кода, обеспечивающего предельное согласование сигнала с каналом, существование которого доказывает. Вместе с тем обосновав принципиальную возможность построения помехоустойчивых кодов, обеспечивающих идеальную передачу.

Если сообщения обладают внутренними корреляционными связями, т. е. если одно сообщение некоторым образом зависит от другого, как это обычно бывает при передаче текстов на естественных языках, то помехоустойчивость любого кода может быть повышена за счет статистических связей между сообщениями. Если эти связи слабые, или неизвестны, или их нельзя использовать для повышения помехоустойчивости, то в этом случае форма представления сообщения должна быть избыточной; в частности, число символов в коде сообщения увеличивают, а между кодовыми символами вводят искусственные корреляционные связи. Поэтому в некоторых случаях помехоустойчивые коды называют избыточными.

Введение избыточности в код позволяет помимо обнаружения и исправления ошибок повысить энергетическую эффективность линии связи, обузить частотный спектр передаваемого сигнала, сократить время вхождения в связь путем повышения помехозащищенности тракта синхронизации, улучшить корреляционные свойства ансамбля сигналов, простыми средствами реализовать разнесенный прием.

В каналах действуют искажения сигналов, шумы, помехи, которые в дискретном канале проявляются в виде перехода одного значения символа в другое - ложное (событие, состоящее в появлении ошибки) или неиспользуемое (событие, которое называют стиранием). В зависимости от характера ошибок различают дискретные каналы: симметричный (все ложные значения символов равновероятны), асимметричный (некоторые ложные значения символов обладают большей вероятностью), без памяти (искажение символа не зависит статистически от искажения другого выходного символа), с памятью (искажение символа выходной последовательности зависит статистически от искажения другого символа той же последовательности), со стираниями (наряду с ошибками имеют место стирания символов).

Любой канал связи с ограниченными полосой частот, временем передачи и динамическим диапазоном (значений амплитуд) обладает конечной пропускной способностью. Теоретически пропускная способность - это максимальное число переданных двоичных единиц (бит) в единицу времени при сколь угодно малой вероятности ошибок. Реально получаемое число передаваемых бит в единицу времени называют скоростью передачи. При неограниченно малой вероятности ошибок скорость передачи всегда меньше пропускной способности. В канале с ошибками максимальное значение скорости получают путем использования помехоустойчивого кодирования. Последнее требует введения избыточности в передаваемый сигнал: по времени, частоте или амплитуде. Если код согласован с каналом, т. е. код позволяет исправлять наиболее вероятные ошибки, введенная избыточность становится оправданной. Если код не согласован с каналом, ошибки могут быть не только не исправлены, но и размножены кодом. В этом случае применение помехоустойчивого кодирования принесет не пользу, а вред. Для согласования кода с каналом связи необходимо иметь максимальный объем сведений о возможных мешающих влияниях в каналах.

Рассмотрим основополагающие принципы, заложенные в основу построения помехоустойчивых кодов. Как следует из доказательства основной теоремы Шеннона, неприменимым свойством помехоустойчивых кодов является наличие избыточности. При этом необходима не просто любая избыточность, а специфическая, определяемая свойствами канала и правилом построения кода. И позволяющая с минимальными затратами повысить вероятность передачи. В ситуации, когда источник сообщений обладает собственной существенной избыточностью, которая в принципе тоже в определенной степени повышает достоверность передачи информации, но не так эффектно как это возможно. Поступают следующим образом: сначала с помощью эффективного кодирования до минимума уменьшают избыточность источника сообщений, а затем в процессе помехоустойчивого кодирования вносят в передаваемый сигнал избыточность, позволяющую простыми средствами поднять верность. Таким образом, эффективное кодирование может сочетаться с помехоустойчивым.

Помехоустойчивые коды можно подразделить на два больших класса блочные и непрерывные. В случае блочных кодов, при кодировании, каждому дискретному сообщению ставится в соответствие отдельный блок кодовых символов называемого кодовой комбинацией. Непрерывные коды образуют последовательность символов неразделяемых на кодовые комбинации.

Рассмотрим принцип построения помехоустойчивых блочных кодов. Избыточность, обуславливающая корректирующие свойства равномерного блочного кода, обычно вводится за счет выполнения неравенства

mⁿ>M (3.73),

где m-основание кода, т.е. объем алфавита используемых кодовых символов, n-длина или количество разрядов кодовой комбинации, М-количество сообщений подлежащих кодированию. Выполнение этого неравенства означает, что для передачи знаков сообщения используют лишь часть М возможных кодовых комбинаций. Используемые кодовые комбинации называют разрешенными. Неиспользуемые mⁿ - M комбинации являются запрещенными. На вход канала подаются только разрешенные комбинации. Если вследствие помех один или несколько символов приняты ошибочно, то на выходе канала появляется запрещенная комбинация, что и говорит о наличии ошибки. Для того, чтобы обеспечить выполнение (3.73) необходимо выбирать n > K , где К-минимальное целое, удовлетворяющее неравенству

m^k M (3.74).

Число К обычно называют количеством информационных разрядов кодовой комбинации, поскольку именно столько разрядов должна содержать комбинация кода с основанием m, чтобы число разных кодовых комбинаций было не меньше числа сообщений М подлежащих передаче. R=n-K разрядов кодовой комбинации необходимых для передачи полезной информации называются проверочными. Количество их и определяет избыточность помехоустойчивого кода. При использовании помехоустойчивого кода возможно декодирование с обнаружением и исправлением ошибок. В первом случае на основе анализа принятой комбинации выясняется, является ли она разрешенной или запрещенной. После этого запрещенная комбинация либо отбрасывается, либо уточняется путем посылки запроса на повторение переданной информации. Во втором случае при приеме запрещенной комбинации определенным способом выявляются и исправляются содержащиеся в ней ошибки. Максимальные числа ошибок в кодовой комбинации q и S, которые могут быть обнаружены (q) или исправлены (S) с помощью данного кода называются соответственно обнаруживающей или исправляющей способностью кода. В значении q и S определяются величиной d_min минимальным кодовым расстоянием между ближайшими разрешенными комбинациями. Под кодовым расстоянием понимают количество неодинаковых разрядов в кодовых комбинациях. Величина d_min в помехоустойчивом коде зависит от соотношения n и К, т.е. от числа r проверочных разрядов кода.

Рассмотрим информационный подход позволяющий оценить необходимую минимальную избыточность, выраженную в количестве проверочных разрядов r_min блочного помехоустойчивого кода, длиной n с заданной исправляющей способностью S. Пусть имеется код с основанием m и с исправляющей способностью S. И используется декодирование с исправлением ошибок. На приеме при использовании такого кода возможно две ситуации: правильный прием сообщения и неправильный. Осуществление с вероятностью P_H. Неправильный прием может произойти в том случае, когда из-за превышения числом ошибок пришедшей из канала кодовой комбинации значение S она может превратиться в одну из других разрешенных кодовых комбинаций. В свою очередь правильный прием осуществляется либо в том случае, когда в принимаемой комбинации отсутствуют ошибки (обозначим вероятность такого сообщения Р₀), либо N_прав в случаях когда в принятой комбинации присутствуют ошибки которые могут быть исправлены рассмотренным кодом. Вероятности таких случаев обозначим через P_j (j=1 N_прав). Для решения поставленной задачи определим минимальное количество информации, которой может быть описана совокупность событий, включающая появление одной из конкретных ошибок и отсутствие ошибок или появление некорректных ошибок. Зная эту величину и максимальное количество информации, которое может содержать один проверочный символ кода можно определить минимальное число проверочных символов.

Количество информации необходимо для описания указанных событий

(3.75)

(в случае отсутствия ошибки учтем включением нуля в предел суммирования). Максимальное количество информации, которое может содержать символ кода с основанием m равно log₂ m. Следовательно, число проверочных разрядов в комбинации кода не может быть меньше, чем

(3.76).

Определенную таким образом величину r_min называют информационным пределом избыточности. Найдем значение r_min для двоичного канала с независимыми ошибками. В таком канале появление предыдущей ошибки не влечет за собой появление последующей. В этой ситуации число R(i) ошибок кратности i в кодовой комбинации длиной n равно числу сочетаний .

(3.77)

Поскольку ошибки независимы вероятность P(i) возникновения в кодовой комбинации ошибки кратности i равна

Р(i) = Pⁱ - (1-P)^n-i (3.78),

где Р-вероятность ошибки в канале. Учитывая, что в данном случае N_пр=S выражение (3.75) можно записать в виде

.

Вторым слагаемым можно пренебречь поскольку, описываемая им функция не используется в процессе исправления ошибок. Поэтому с учетом (3.77 и 3.78) имеем

(3.79).

Рассмотрим частный случай, когда возникновение конкретной ошибки любой кратности и отсутствие ошибок имеют равную вероятность, т.е. , при любом i. Величину Р₁ определим из условия нормировки

(3.80),

отражающего тот факт, что вероятность появления ошибки какой-либо кратности, включения и нулевую равна единице. Из (3.80) имеем

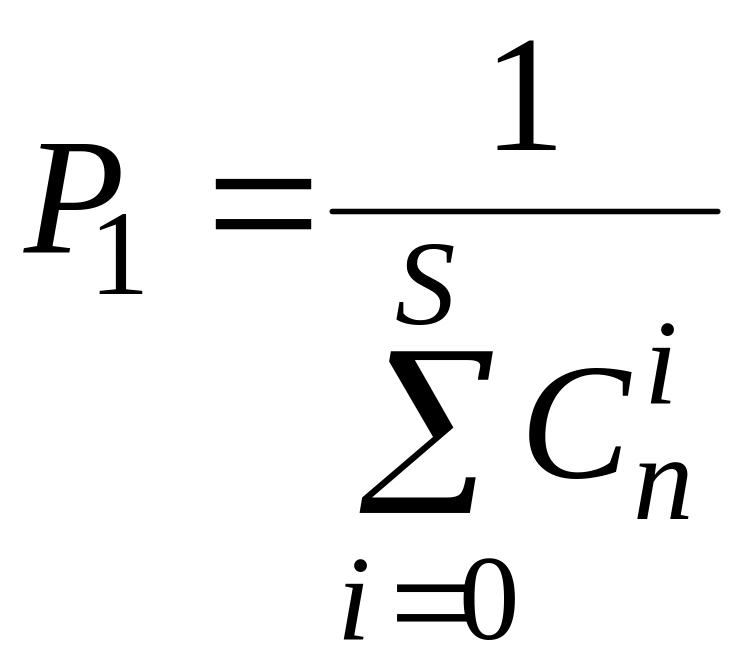
следовательно,

(3.81).

Поскольку код двоичной, то есть m=2, c учетом (3.76 и 3.81), имеем

.

Найденное таким образом значение r_min совпадает с оценками полученными другим методами в частности с нижним пределом Хэмминга. Аналогичным образом могут быть найдены информационные пределы избыточности для других конфигураций ошибок в канале, например для пакетных ошибок, когда одиночные ошибки группируются в пакеты различной кратности. Полученные при этом результаты так же хорошо согласовывается с выводами полученными другими методами. Найденное таким образом значение r_min совпадает с оценками, полученными другими методами, в частности, с нижним пределом Хэмминга. Аналогичным образом могут быть найдены информационные пределы избыточности для других конфигураций ошибок в канале, например для пакетных ошибок, когда одиночные ошибки группируются в пакеты различной кратности. Получаемые при этом результаты также хорошо согласуются с выводами, полученными другими методами.

К настоящему времени разработано много различных помехоустойчивых кодов, отличающихся друг от друга основанием q, расстоянием d, избыточностью, структурой, функциональным назначением, энергетической эффективностью, корреляционными свойствами, алгоритмами кодирования и декодирования, формой частотного спектра. На рисунке, представленном выше, приведены типы кодов, различающиеся по особенностям структуры, функциональному назначению, физическим свойствам кода как сигнала.

Наиболее важный подкласс непрерывных кодов образуют сверточные коды, отличающиеся от других непрерывных кодов методом построения и более широкой областью применения.

В общем случае, чем длиннее код при фиксированной избыточности, тем больше расстояние и тем выше помехоустойчивость кода. Однако длинные коды сложно реализуются. Составные коды дают компромиссное решение задачи; из них основное значение имеют каскадные коды и коды произведения. Как правило, каскадный код состоит из двух ступеней (каскадов): внутренней и внешней. По линии связи сигналы передают внутренним кодом n_вт, символьные слова которого являются символами внешнего кода длины n_вш. Основание внешнего кода равно q^k_вт.

Коды произведения строят в виде матрицы, в которой строки суть слова одного кода, а столбцы - того же или другого кода.

При формировании каскадного кода входную информационную последовательность символов разбивают на блоки по k_вт символов в каждом, каждый блок сопоставляют с информационным символом внешнего кода из алфавита, содержащего q^k_вт значений символов. Затем k_вш информационных символов внешнего кода преобразуют в блоки из n_вш символов внешнего кода и, наконец, блоки из k_вт информационных символов внутреннего кода преобразуют в блоки из n_вт символов внутреннего кода. Возможны различные варианты: внешний и внутренний коды - блочные, внешний блочный - внутренний сверточный, внешний сверточный - внутренний блочный, внешний и внутренний сверточные.

Один из наиболее распространенных методов формирования кода произведения заключается в последовательной записи по k₁ символов входной информационной последовательности в k₂ строк матрицы (например, в ячейки памяти ОЗУ), добавлении избыточных символов по n₁-k₁ в каждую строку и по n₂-k₂ в каждый столбец, после чего в последовательность символов кода считывают по строкам или столбцам из матрицы. Физическим аналогом кода произведения является, в частности, частотно-временной код, у которого строки располагаются вдоль оси времени, а столбцы - по оси частот.

Параметры составных кодов: каскадных - n=n_вшn_вт, k=k_вшk_вт, d=d_вшd_вт; произведения - n=n₁n₂, k=k₁k₂, d=d₁d₂.

Производные коды строят на основе некоторого исходного кода, к которому либо добавляют символы, увеличивая расстояние (расширенный код), либо сокращают часть информационных символов без изменения расстояния (укороченный код), либо выбрасывают (выкалывают) некоторые символы (выколотый, или перфорированный код). Код Хэмминга дает пример процедуры расширения, увеличивающей расстояние кода с 3 до 4. Необходимость в выкалывании возникает в результате построения на основе исходного кода другого, менее мощного, более короткого кода с тем же расстоянием.

При более широкой трактовке термина "производный код" к этому классу можно отнести все коды, полученные из исходного добавлением или исключением как символов, так и слов.

Формально деление кодов на двоичные и недвоичные носит искусственный характер; по аналогии следует выделять троичные, четверичные и другие коды большего основания. Оправдывается такое деление усложнением алгоритмов построения, кодирования и декодирования недвоичных кодов.

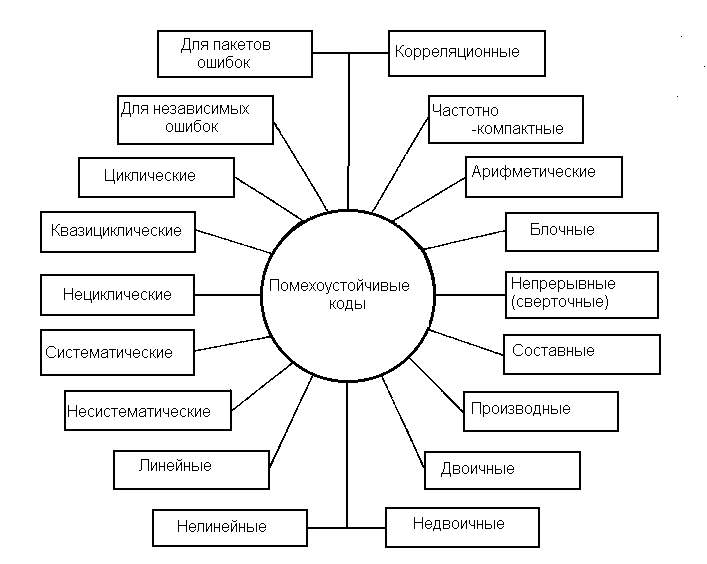Рис.3.3. Классификация помехоустойчивых кодов

При прочих равных условиях желательно, чтобы информационные и избыточные символы располагались отдельно. В систематических кодах это условие выполняется.

В циклических кодах каждое слово содержит все свои циклические перестановки. Все n циклических перестановок (слова длины n) образуют цикл. В квазициклических кодах цикл образуется на числе символов n-1 или, реже, n-2. Циклические коды важны как с точки зрения математического описания, так и для построения и реализации кода.

Ошибки в каналах связи имеют самое различное распределение, однако, для выбора помехоустойчивого кода целесообразно разделить все возможные конфигурации ошибок на независимые (некоррелированные) и пакеты (коррелированные ошибки). На практике приходится учитывать качество интервалов между пакетами: они могут быть свободными от ошибок или же содержать случайные независимые ошибки.

Под корреляционными подразумевают коды, обладающие хорошими корреляционными свойствами, важными при передаче сигналов вхождения в связь, для повышения защищенности от некоторых видов помех, извлечения сигналов из интенсивных шумов, обеспечения многостанционного доступа, построения асинхронно-адресных систем связи. Корреляционные коды включают в себя пары противоположных сигналов с хорошей функцией автокорреляции (метод внутриимпульсной модуляции), импульсно-интервальные коды, имеющие на фиксированном интервале времени постоянное для всех слов кода число импульсов с неперекрывающимися (при любом взаимном сдвиге слов во времени) значениями интервалов между импульсами, ансамбли сигналов с хорошими взаимокорреляционными свойствами.

Особый класс образуют частотно-компактные коды, предназначенные для сосредоточения энергии сигнала в возможно более узкой полосе частот. Столь общая постановка задачи понимается в различных системах связи по-разному: в проводных линиях и линейных трактах, содержащих полосно-ограничивающие фильтры с крутыми фронтами, необходимо основную энергию сигналa "отодвинуть" от крайних частот к центру полосы пропускания целью уменьшения межсимвольных искажений; в сетях радиосвязи с жесткими ограничениями по электромагнитной совместимости радиосредств от кода требуется значительно (на десятки децибел) уменьшить уровень внеполосных излучений. Построение кодирование и декодирование частотно-компактных кодов существенно зависят от метода модуляции.

Арифметические коды служат для борьбы с ошибками при вы полнении арифметических операций в процессоре ЭВМ.

Коды можно разделить на линейные и нелинейные. Линейные коды образуют векторное пространство и обладают следующим важным свойством: два кодовых слова можно сложить, используя подходящее определение суммы, и получить третье кодовое слово. В случае обычных двоичных кодов эта операция является посимвольным сложением двух кодовых слов по модулю 2 (т. е. 1+1=0, 1+0=1, 0+0=0). Это свойство приводит к двум важным следствиям. Первое из них состоит в том, что линейность существенно упрощает процедуры кодирования и декодирования, позволяя выразить каждое кодовое слово в виде "линейной" комбинации небольшого числа выделенных кодовых слов, так называемых базисных векторов. Второе свойство состоит в том, что линейность существенно упрощает задачу вычисления параметров кода, поскольку расстояние между двумя кодовыми словами при этом эквивалентно расстоянию между кодовым словом, состоящим целиком из нулей, и некоторым другим кодовым словом. Таким образом, при вычислении параметров линейного кода достаточно рассмотреть, что происходит при передаче кодового слова, состоящего целиком из нулей. Вычисление параметров упрощается еще и потому, что расстояние Хемминга между данным кодовым словом и нулевым кодовым словом равно числу ненулевых элементов данного кодового слова. Это число часто называют весом Хемминга данного слова, и список, содержащий число кодовых слов каждого веса, можно использовать для вычисления характеристик кода с помощью аддитивной границы. Такой список называют спектром кода.

Линейные коды отличаются от нелинейных замкнутостью кодового множества относительно некоторого линейного оператора, например сложения или умножения слов кода, рассматриваемых как векторы пространства, состоящего из кодовых слов - векторов. Линейность кода упрощает его построение и реализацию. При большой длине практически могут быть использованы только линейные коды. Вместе с тем часто нелинейные коды обладают лучшими параметрами по сравнению с линейными. Для относительно коротких кодов сложность построения и реализации линейных и нелинейных кодов примерно одинакова.

Как линейные, так и нелинейные коды образуют обширные классы, содержащие много различных конкретных видов помехоустойчивых кодов. Среди линейных блочных наибольшее значение имеют коды с одной проверкой на четность, M-коды (симплексные), ортогональные, биортогональные, Хэмминга, Боуза-Чоудхури-Хоквингема, Голея, квадратично-вычетные (KB), Рида-Соломона. К нелинейным относят коды с контрольной суммой, инверсные, Нордстрома-Робинсона (HP), с постоянным весом, перестановочные с повторением и без повторения символов (полные коды ортогональных таблиц, проективных групп, групп Матье и других групп перестановок).

Почти все схемы кодирования, применяемые на практике, основаны на линейных кодах. Двойные линейные блоковые коды часто называют групповыми кодами, поскольку кодовые слова образуют математическую структуру, называемую группой. Линейные древовидные коды обычно называют сверточными кодами, поскольку операцию кодирования можно рассматривать как дискретную свертку входной последовательности с импульсным откликом кодера.

Наконец, коды можно разбить на коды, исправляющие случайные ошибки, и коды, исправляющие пакеты ошибок. В основном мы будем иметь дело с кодами, предназначенными для исправления случайных, или независимых, ошибок. Для исправления пакетов ошибок было создано много кодов, имеющих хорошие параметры. Однако при наличии пачек ошибок часто оказывается более выгодным использовать коды, исправляющие случайные ошибки, вместе с устройством перемежения восстановления. Такой подход включает в себя процедуру перемешивания порядка символов в закодированной последовательности перед передачей и восстановлением исходного порядка символов после приема с тем, чтобы рандомизировать ошибки, объединенные в пакеты.

3.5. Основные принципы помехоустойчивого кодирования

Кодирование с исправлением ошибок, по существу, представляет собой метод обработки сигналов, предназначенный для увеличения надежности передачи по цифровым каналам. Хотя различные схемы кодирования очень непохожи друг на друга и основаны на различных математических теориях, всем им присущи два общих свойства. Одно из них - использование избыточности. Закодированные цифровые сообщения всегда содержат дополнительные, или избыточные, символы. Эти символы используют для того, чтобы подчеркнуть индивидуальность каждого сообщения. Их всегда выбирают так, чтобы сделать маловероятной потерю сообщением его индивидуальности из-за искажения при воздействии помех достаточно большого числа символов. Второе свойство состоит в усреднении шума. Эффект усреднения достигается за счет того, что избыточные символы зависят от нескольких информационных символов. Для понимания процесса кодирования полезно рассмотреть каждое из этих свойств отдельно.

Рассмотрим вначале двоичный канал связи с помехами, приводящими к тому, что ошибки появляются независимо в каждом символе и средняя вероятность ошибки равна Р=0,01. Если требуется рассмотреть произвольный блок из 10 символов на выходе канала, то весьма трудно выявить символы, которые являются ошибочными. Вместе с тем если считать, что такой блок содержит не более трех ошибок, то мы будем неправы лишь два раза на миллион блоков. Кроме того, вероятность, что мы окажемся правы, возрастает с увеличением длины блока. При увеличении длины блока доля ошибочных символов в блоке стремится к средней частоте ошибок в канале, а также, что очень важно, доля блоков, число ошибок, в которых существенно отличается от этого среднего значения, становится очень малой. Простые вычисления помогают понять, насколько верным является это утверждение.

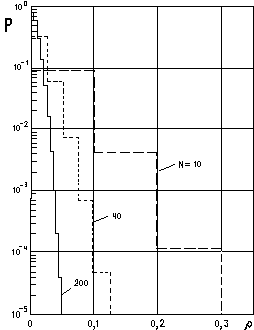Рис. 3.4. Вероятность того, что доля ошибочных символов e/N в блоке длиной N превышает  при вероятности Р _e=0,01

Рассмотрев, например, тот же канал, вычислим вероятность того, что доля ошибочных символов превышает значение , и построим график этой функции для нескольких значений длины блока.

Кривые на рис. 3.4 показывают, что при обработке символов блоками, а не одного за другим можно уменьшить общую частоту ошибок. При этом потребуется, чтобы существовала схема кодирования, нечувствительная к ошибкам в некоторой доле символов блока и не приводящая при этом к потере сообщением своей индивидуальности, т. е. не приводящая к ошибочному блоку. Из графиков на рис. 3.4 для различных длин блоков видно, какую именно долю ошибок нужно исправлять, чтобы получить заданную вероятность ошибки блока. Он показывает также, что при фиксированной вероятности ошибки блока доля ошибок, которые нужно исправлять, уменьшается при возрастании длины блока. Сказанное свидетельствует о резервах улучшения характеристик при усреднении шума и о том, что эти резервы возрастают при увеличении длины блока. Таким образом, длинные блоковые коды эффективнее коротких. После того как установлена целесообразность исправления ошибок в символах, возникает следующий логичный вопрос: как это сделать? Ключ лежит в избыточности. При исправлении ошибок в сообщении, представляемом последовательностью из n двоичных символов, очень важно учесть, чтобы не все 2ⁿ возможных последовательностей представляли сообщения. В самом деле, когда каждая из возможных принятых последовательностей n символов представляет некоторое сообщение, нет никаких оснований считать, что одна последовательность является более правильной, чем любая другая. Продолжая рассуждать таким же способом, можно ясно увидеть, что для исправления всех наборов из t или менее ошибок необходимо и достаточно, чтобы каждая последовательность, представляющая сообщение, отличалась от последовательности, представляющей любое другое сообщение, не менее чем в 2t+1 местах. Например, для исправления всех одиночных или всех двойных ошибок в символах нужно, чтобы каждые две последовательности, представляющие разные сообщения, отличались не менее чем в пяти символах. Каждая принятая последовательность, содержащая два ошибочных символа и, следовательно, отличающаяся от посланной последовательности ровно в двух местах, будет всегда отличаться от всех других последовательностей, представляющих сообщения, не менее чем в трех местах. Число позиций, в которых две последовательности отличаются друг от друга, будем называть расстоянием Хемминга d между этими двумя последовательностями. Наименьшее значение d для всех пар кодовых последовательностей называется кодовым расстоянием и обозначается d_min. Поскольку d_min всегда должно быть на единицу больше удвоенного числа исправляемых ошибок, можно написать

t = [(d_min- l) / 2], (3.82)

где [ ] обозначает целую часть. Параметр t указывает, что все комбинации из t или менее ошибок в любой принятой последовательности могут быть исправлены. Имеются модели каналов, в которых значение t может быть больше указанного в (3.82).

Рассмотрим код, состоящий из четырех кодовых слов 00000, 00111,11100 и 11011. Каждое кодовое слово используется для представления одного из четырех возможных сообщении. Поскольку код включает лишь небольшую долю всех 32 возможных последовательностей из пяти символов, мы можем выбрать кодовые слова таким образом, чтобы каждые два из них отличались друг от друга не менее чем в трех позициях. Таким образом, кодовое расстояние равно трем и код может исправлять одиночную ошибку в любой позиции. Чтобы провести процедуру декодирования при этом коде, каждой из 28 недопустимых последовательностей нужно поставить в соответствие ближайшую к ней допустимую последовательность. Этот процесс ведет к созданию таблицы декодирования, которая строится следующим образом. Вначале под каждым кодовым словом выписываем все возможные последовательности, отличающиеся от него в одной позиции. В результате получаем часть табл. 1.2, заключенную между штриховыми линиями. Заметим, что после построения этой части осталось 8 последовательностей. Каждая из этих последовательностей отличается от каждого кодового слова не менее чем в двух позициях. Однако в отличие от других последовательностей эти восемь последовательностей нельзя однозначно разместить в таблице. Например, последовательностью можно поместить либо в первый, либо в четвертый столбец. При использовании этой таблицы в процессе декодирования нужно найти столбец, в котором содержится принятая последовательность, и а качестве выходной последовательности декодера взять кодовое слово, находящееся в верхней строке этого столбца.

Таблица 2.

Таблица декодирования для кода с четырьмя словами

00000 10000 01000 00100 00010 00001	11100 01100 10100 11000 11110 11101	00111 10111 01111 00011 00101 00110	11011 01011 10011 11111 11001 11010
10001 10010	01101 01110	10110 10101	01010 01001

Причина, по которой таблица декодирования должна строиться именно таким образом, очень проста. Вероятность появления фиксированной комбинации из i ошибок равна Р^t_e(1 -Р_e)^5-i . Заметим, что при Р_e<1/2

(1 -Р_e)⁵P_e(1 -Р_e)⁴Р_e²(1 -Р_e)³...

Таким образом, появление фиксированной одиночной ошибки более вероятно, чем фиксированной комбинации двух ошибок, и т. д. Это значит, что декодер, который декодирует каждую принятую последовательность в ближайшее к ней по расстоянию Хемминга кодовое слово, выбирает в действительности то кодовое слово, вероятность передачи которого максимальна (в предположении, что все кодовые слова равновероятны). Декодер, реализующий это правило декодирования, является декодером максимального правдоподобия, и в указанных предположениях он минимизирует вероятность появления ошибки декодирования принятой последовательности. В этом смысле такой декодер является оптимальным. Это понятие очень важно, поскольку декодеры максимального правдоподобия часто используются для коротких кодов. Кроме того, параметры декодера максимального правдоподобия могут служить эталоном, с которым сравниваются параметры других, неоптимальных декодеров. Если декодирование ведется с помощью таблицы декодирования, то элементы таблицы можно расположить так, чтобы получить декодирование по максимуму правдоподобия. К сожалению, объем таблицы растет экспоненциально с ростом длины блока, так что использование таблицы декодирования для длинных кодов нецелесообразно. Однако таблица декодирования часто оказывается полезной для выяснения важных свойств блоковых кодов.

Множество кодовых слов в таблице декодирования является подмножеством (первой строкой таблицы декодирования) множества всех 2ⁿ последовательностей длиной n. В процессе построения таблицы декодирования множество всех последовательностей длиной n разбивается на непересекающиеся подмножества (столбцы таблицы декодирования). В случае когда код исправляет t ошибок, число N_e последовательностей длиной n в каждом подмножестве удовлетворяет неравенству

N_e  1+ n + C_n² +...+ C_n^t, (3.83)

где C_nⁱ - i-й биномиальный коэффициент.

Неравенство (3.83) следует непосредственно из того, что имеется ровно n различных последовательностей, отличающихся от данной последовательности в одной позиции, C_n² последовательностей, отличающихся в двух позициях, и т. д. Как и в приведенном выше простом примере, после размещения всех последовательностей, отличающихся от кодовых в t или менее позициях, почти всегда остаются неразмещенные последовательности [отсюда неравенство в (3.83)]. Теперь можно связать избыточность кода c числом ошибок, которые им исправляются. Заметим сначала, что число всех возможных последовательностей равно 2ⁿ. Каждый столбец таблицы декодирования содержит N_e таких последовательностей, поэтому общее число кодовых слов должно удовлетворять неравенству

N_e  2ⁿ / (1+ n + C_n² +...+ C_n^t), (3.84)

Это неравенство называется границей Хемминга или границей сферической упаковки. Равенство в (3.84) достигается только для так называемых совершенных кодов. Эти коды исправляют все наборы из t или менее ошибок и не исправляют никаких других наборов. Число известных совершенных кодов очень невелико, так что равенство в (3.84) достигается в очень редких случаях.

Процесс кодирования состоит в том, что наборы k информационных символов отображаются в кодовые последовательности, состоящие из n символов. Любое такое отображение будем называть (n,k)-кодом, хотя обычно такое название применяется только к линейным кодам. Поскольку число последовательностей длиной k равно 2^k, неравенство (3.84) можно переписать следующим образом:

2^k  2ⁿ / (1+ n + C_n² +...+ C_n^t), (3.85)

Мера эффективности кода определяется отношением

R=k/n (3.86)

и называется скоростью кода. Доля избыточно передаваемых символов равна 1-R.

Отображение, возникающее при кодировании, можно задавать таблицей кодирования. Например, код с четырьмя кодовыми словами задается табл. 3.

Таблица 3.

Таблица поиска при декодировании

Входная последовательность	Кодовая последовательность
00 01 10 11	00100 01111 11011 10000

Часть кодовой последовательности, заключенная между штриховыми линиями, совпадает с входной последовательностью. Поэтому каждой кодовой последовательности, легко однозначно сопоставить входную последовательность. Не все блоковые коды обладают этим свойством. Те, которые им обладают, называются систематическими кодами. Понятие избыточных символов для систематических кодов становится абсолютно ясным, и избыточными символами в табл. 2 являются символы на позициях 1, 4 и 5. Коды, не обладающие указанным свойством, называются несистематическими.

Существует много хороших конструктивных методов кодирования, позволяющих исправлять кратные ошибки и приводящих к заметному уменьшению частоты появления ошибочных символов. Эти коды легко строятся и с помощью современных полупроводниковых устройств относительно просто декодируются. Например, существует блоковый код длиной 40, содержащий 50% избыточных символов и позволяющий исправлять четыре случайные ошибки. На рис. 3.4 показано, что при Р_e=0,01 этот код имеет вероятность ошибки блока, меньшую 10^-4. Если этого недостаточно, разработчик увеличивает избыточность, чтобы исправлять большее число ошибок, или переходит к кодам с большей длиной блока и получает выигрыш за счет большего усреднения. В каждом случае нужно принимать во внимание возникающие дополнительные затраты. Однако обе указанные возможности допустимы и могут представлять практически приемлемые альтернативы.

Форма кривых, изображенных на рис. 3.4, позволяет предположить, что если имеется схема, исправляющая фиксированную долю t/n ошибочных символов в блоке (в нашем случае t/n незначительно превышает 0,01), то, выбирая длину блока достаточно большой, можно сделать долю ошибок сколь угодно малой. К сожалению, это оказывается очень трудной задачей. Большинство конструктивных процедур может обеспечить постоянное отношение t/n лишь при возрастающей доле избыточных символов (другими словами, R0 при n). Таким образом, потеря эффективности возникает из-за того, что доля полезных сообщений становится очень малой при большой длине блока.

4. Непрерывные ансамбли и источники

4.1. Непрерывные ансамбли и источники. Обобщение понятия количества информации

Все предыдущее рассмотрение относилось только к случаю дискретных ансамблей и соответственно к случаю, когда дискретные ансамбли являлись моделями источников сообщений. Класс дискретных источников не исчерпывает всего многообразия источников, встречающихся на практике. Например, источник, порождающий речевые сообщения, не является дискретным, ибо в каждый момент времени выходным сигналом источника является некоторое действительное число — величина звукового давления.

В этом параграфе мы введем непрерывные ансамбли сообщений, которые могут служить моделями источников непрерывных сообщений. Начнем с наиболее простого случая, а именно, ансамбля, соответствующего непрерывной случайной величине (с. в.).

Пусть на числовой оси задано некоторое распределение вероятностей, определяющее с. в. X, и F (х) — функция распределения этой с. в., т. е. такая функция, что ее значение в точке x; равно вероятности появления с. в. X в интервале (—, х]:

F(x)  Pr (— < X  х)

Если существует функция f (х) такая, что для всех х на числовой оси

(4.1)

то она называется функцией плотности вероятностей (ф. п. в.) (или просто плотностью вероятностей) с. в. X. Для любого интервала (а, b] числовой оси вероятность появления с. в. в этом интервале определяется по формуле

Pr (a, b) = F (b) - F (a) = (4.2)

Очевидно, функция F (х) неотрицательна и монотонно не убывает, причем F(—)=0, F()=1. Функция плотности вероятностей неотрицательна и ее интеграл в пределах от — до + равен единице. Последнее условие обычно называют условием нормировки. В зависимости от свойств распределений вероятностей может быть нескольких типов функции F(х). Если эта функция ступенчатая и имеет конечное число ступенек, то распределение называется дискретным и соответствует дискретной случайной величине. В этом случае функции плотности в обычном смысле не существует. Если для F(х) в каждой точке может быть определена производная, то распределение соответствует непрерывной случайной величине. Производная функции распределения в этом случае есть ф. п. в. Указанные два случая — наиболее часто встречающиеся в приложениях. Смешанный тип распределения — это такой, когда F(х) непрерывна (справа) в каждой точке, за исключением конечного числа точек, где функция распределения имеет ступеньки. Наконец, последний тип распределения имеет место, когда F(х) непрерывна в каждой точке (справа), но ф. п. в. всюду или на каком-либо интервале не существует.

Пример 4.1. Рассмотрим дискретную случайную величину — число очков при бросании кости. Возможные значения для этой с. в. суть 1, 2, ..., 6. Очевидно, F (х) = [x] / 6, где [x] — целая часть х, F (х) = О при х < 1 и F(х) = 1 при х  6 (см. рис. 3.2).

Пример 4.2. Рассмотрим непрерывную с. в., которая задается функцией распределения

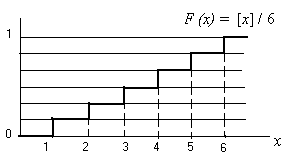
Рис. 4.1. Функция распре-деления числа очков при бросании игральной кости

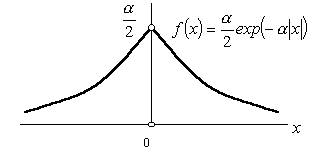
Рис. 4.2. Функция плотности вероятности непрерывной с.в. примера 4.2.

(4.3)

Нетрудно найти ф. п. в. этого распределения (см. рис. 4.2)

(4.4)

Пример 4.3. На рис. 4.3 показана функция распределения смешанного типа. Все значения, кроме х = 1 и х = 2, имеют нулевые вероятности (но не плотности v вероятностей), как для любой непрерывной с. в. Значения х = 1, х = 2 появляются с ненулевыми вероятностями, как в дискретном случае.

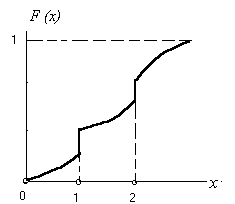
Рис. 4.3. Функция распределения смешанного типа

Непрерывным ансамблем, задаваемым ф.п.в. f (х), будем называть пару {X, f (х)}, где X — числовая ось и распределение вероятностей на X задается ф. п. в. f(х).

Согласно этому определению мы отождествляем понятия непрерывного ансамбля и непрерывной действительной случайной величины, имеющей ф. п. в. f(х). Система совместно заданных непрерывных ансамблей вводится таким же образом, как и в случае дискретных ансамблей. Пусть X и Y — числовые оси и XY (произведение множеств X и Y) — действительная плоскость, т. е. множество всех упорядоченных пар (x, у), где х  X и у  Y. Пусть F(х, у) — совместная функция распределения на множестве XY, Функции распределения на множествах X и Y при этом определяются из соотношений

F₁ (х) = F (х, ), F₂ (у) = F(, у) (4.5)

соответственно.

Пусть распределения вероятностей на X, Y и XY задаются ф. п. в. f₁ (х), f₂ (у) и f (х, у), причем f (х, у) определяется соотношением

(4.6)

а

(4.7)

В этом случае будем говорить, что {XY, f (х, у)} есть система двух совместно заданных непрерывных ансамблей {X , f _l (х)} и {Y, f ₂ (y)}

Всякий раз, как совместно заданы два непрерывных ансамбля, определено семейство различных условных непрерывных ансамблей. Так, если фиксировано сообщение у  Y, для которого f₂(у)  0, то на множестве X определена условная ф. п. в.

(4.8)

и условный непрерывный ансамбль {X, f (х | у)}. Аналогичным образом определяется условный непрерывный ансамбль {Y, f (y | x)}.

Система более двух непрерывных ансамблей вводится в точности так же, как система двух ансамблей. Пусть Х_l ... Х_п — произведение п множеств, каждое из которых является числовой прямой. Элементы множества Х₁ ... Х_п представляют собой действительные последовательности (х⁽¹⁾, ..., х^(п)) длины п, х⁽¹⁾  X₁, ..., х^(п) Х_п. Будем считать, что распределение вероятностей на этом множестве задается n-мерной ф. п. в. f(х⁽¹⁾, ..., х^(п)). Другими словами, для любого набора интервалов ₁, ..., _n вероятность попадания последовательности (x⁽¹⁾, ..., х^(п)) в n-мерную область, задаваемую указанными интервалами, определяется n-кратным интегралом

Пусть

(4.9)

Соотношения (4.9) задают безусловные ф. п. в. на множествах Х₁, ..., Х_п соответственно. В этом случае будем говорить, что {X₁ ... Х_п, f(х⁽¹⁾ ..., х⁽ⁿ⁾)} есть система п совместно заданных непрерывных ансамблей {Х₁, f₁ (x)} ,..., {Х_п , f_n (х)}. Если

f ( х⁽¹⁾ ,..., х ⁽ⁿ⁾) = f₁ ( x ⁽¹⁾) . . . f_n ( x ⁽ⁿ⁾) (4.10)

для любых x⁽¹⁾  Х₁ ,..., х^(п)  Х_п, то непрерывные ансамбли Х₁, ..., Х_п называются статистически независимыми.

Заметим, что при задании системы п непрерывных ансамблей фактически оказываются заданными всевозможные системы по тп непрерывных ансамблей.

Пусть {Х, f₁(х)} — непрерывный ансамбль и (х) — произвольная действительная функция на X, отображающая числовую прямую X в себя. Всякая такая функция порождает некоторый ансамбль и называется случайной величиной на ансамбле {X, /! (х)\. Если ф (х) — ступенчатая функция с конечным числом значений, то она порождает дискретный ансамбль {Y, р (у)}, где Y = {y₁, ..., y_n} — множество значений функции  (х) и

Если  (х) — непрерывная функция, то она порождает непрерывный ансамбль {Y, }, где Y — числовая ось, а ф. п. в. определяется из уравнения

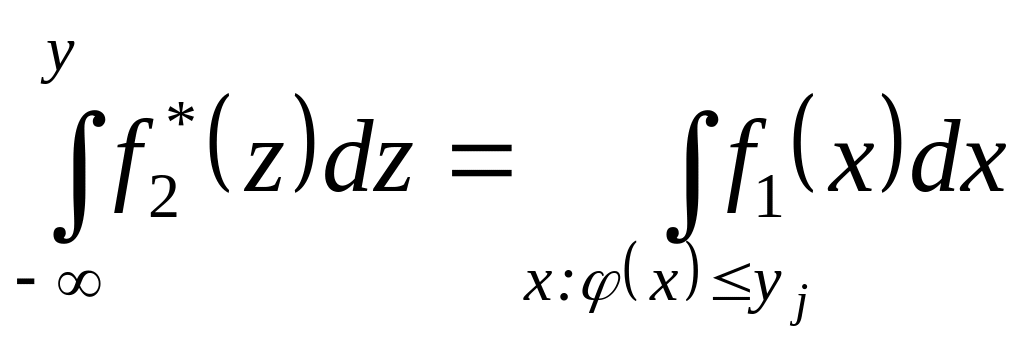
Для каждой с. в. определены ее числовые характеристики, например, математическое ожидание и дисперсия. Все числовые характеристики непрерывных случайных величин определяются так же, как и в случае дискретных случайных величин с заменой вероятностей на ф. п. в. и сумм на интегралы. Очевидно, что для непрерывных с. в. справедливо неравенство Чебышева и закон больших чисел.

Рассмотрим теперь совместное задание непрерывного ансамбля X и дискретного ансамбля Y_д. Для этого удобно рассматривать дискретный ансамбль как результат дискретизации некоторого непрерывного ансамбля Y. Пусть {XY, f (х, у)} — пара совместно заданных непрерывных ансамблей {X, f_l (х)} и {Y, f₂ (y)}. Пусть B₁, ..., B_N — разбиение множества Y на непересекающиеся подмножества. Введем в рассмотрение дискретное множество Y_д={y_l, …, y_N} и будем говорить, что происходит событие y_j, если точка непрерывного ансамбля {Y, f₂ (у)} попадает в множество В_j. Для каждого у вероятность р₂ (y_j) этого события определяется формулой

(4.11)

Переход от непрерывного ансамбля {Y, f₂ (у)} к дискретному называется дискретизацией. Очевидно, что любой дискретный ансамбль можно себе представлять как результат дискретизации некоторого непрерывного.

Так же, как и в дискретном случае, разбиение Y на подмножества задает семейство условных плотностей вероятностей на множестве X

(4.12)

Отсюда и из (4.7) следует, что

(4.13)

С другой стороны, на дискретном множестве Y_д определены условные вероятности

(4.14)

Таким образом, ансамбль X задается ф. п. в. f_l (х), ансамбль Y_д—распределением вероятностей p₂ (y_j), а ансамбль ХY_д задается двумя эквивалентными способами: либо посредством функции

f₁ (х) p(y_j| х), х X, у_j  Y_д (4.15)

либо посредством функции

f (х|y_j) p(y_j), х X, у_j  Y_д (4.16)

Соотношение (4.14) показывает, что обе эти функции совпадают и определяют следующую функцию распределения на множестве ХY_д:

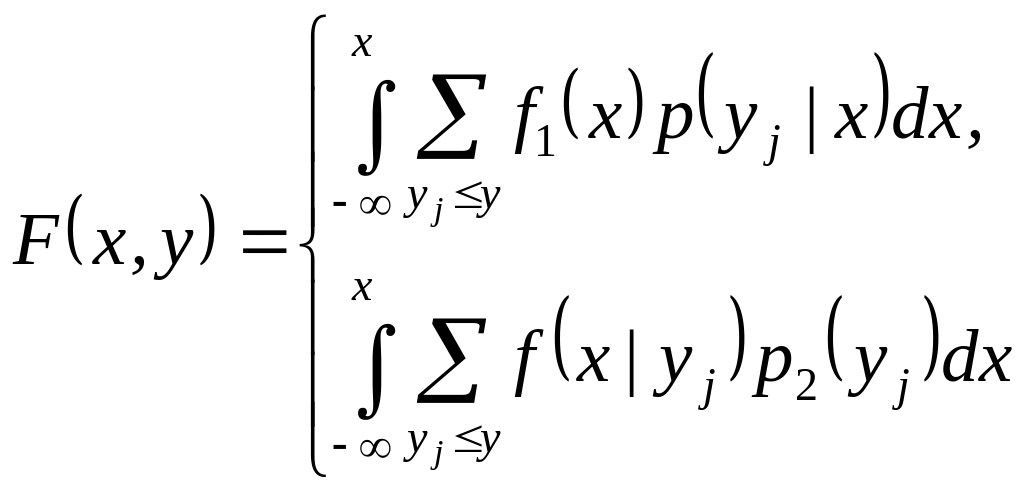(4.17)

При рассмотрении различных функций на числовых множествах и изучении их свойств часто бывает необходимо рассматривать одновременно и дискретные и непрерывные распределения вероятностей. Такое общее рассмотрение можно осуществить с помощью функций распределений. Однако многие результаты, относящиеся к непрерывным распределениям, традиционно излагаются в терминах плотностей вероятностей и в этой форме имеют более простой вид, чем в форме, использующей функции распределения. Поэтому желательно также иметь описание дискретных распределений с помощью функций, имеющих смысл функций плотностей вероятностей. Далее мы рассмотрим дельта-функцию Дирака (одну из так называемых обобщенных функций) и используем ее для задания плотностей вероятностей дискретных случайных величин.

Дельта-функция Дирака,  (х), определяется следующим формальным равенством:

(4.18)

где  (х) — произвольная непрерывная функция и  — произвольный интервал на числовой оси. Очевидно, что

(4.19)

и

(4.20)

Дельта-функцию можно умножать на число, складывать с другими дельта-функциями и складывать с обычными интегрируемыми функциями. Отдельно аналитические свойства дельта-функции не исследуются (хотя и можно представлять функцию  (х), например, как предел последовательности сужающихся импульсов с единичной площадью). Она имеет смысл только в выражениях вида (4.18).

Покажем теперь, как используется дельта-функция для описания дискретных с. в. Пусть X = {x₁, ..., х_M} — произвольное числовое множество и {p₁, ..., р_M} —распределение вероятностей на X. Очевидно, что функция распределения F (х) = . где суммирование выполняется по всем таким индексам i, что x_i  х. В этом случае

(4.21)

есть формальное выражение для обобщенной ф. п. в указанного дискретного распределения, так как

(4.22)

Если на произведении XY дискретных множеств X = {x_l, ..., x_M}, Y={y_l ,…, y_M} задано распределение вероятностей р (х_i, у_j), то обобщенная ф. п. в. этого распределения

(4.23)

Безусловные ф. п. в. определяются обычным образом:

Отношение выражений, содержащих дельта-функции, вообще говоря, не определено, и поэтому условные ф. п. в., например f^* (x | y) = f^* (x, y) / f^*(у), не являются ни обычными, ни обобщенными ф. п. в. Однако, если положить

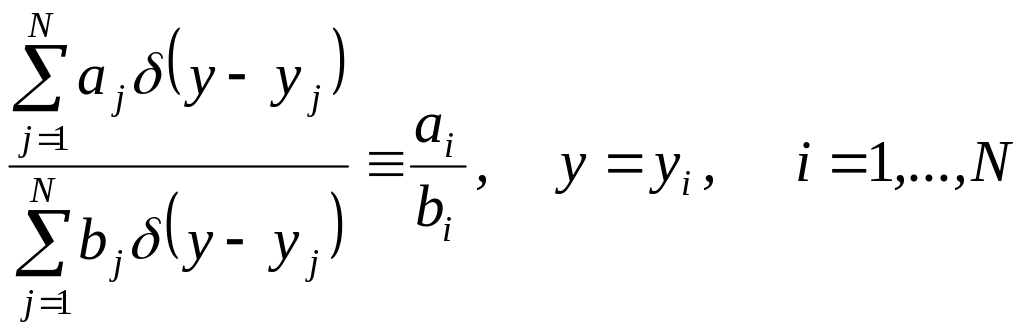(4.24)

Для всех выражений такого вида с ненулевыми коэффициентами b_i , то

(4.25)

где

и функция f^* (x | y) становится обобщенной ф. п. в. для всех у = y_j j=1, 2, ..., W. Для остальных у эта функция не определена. Кроме того,

(4.26)

где

Введем теперь количество информации между сообщениями непрерывных ансамблей. В дискретном случае взаимная информация определялась через количество собственной информации в сообщении . Однако в случае непрерывных-ансамблей вероятность каждого отдельного сообщения равна нулю, и, следовательно, собственная информация сообщений бесконечна. С физической точки зрения бесконечно большая собственная информация соответствует тому, что всякая непрерывная с. в. принимает бесконечное число значений, каждое из которых можно рассматривать как некоторое сообщение. Хотя собственная информация сообщений непрерывного ансамбля бесконечно велика, взаимная информация между парой сообщений, как правило, ограничена.

Количеством взаимной информации между сообщениями х  X, у  Y непрерывного ансамбля {XY,f (х,у)} называется величина

(4.27)

определенная для всех пар (х, у) таких, что f(х)  0, f(у)  0. Для остальных пар сообщений количество взаимной информации I (х; у) в случае необходимости доопределяется произвольным образом.

Заметим, что из (4.26) вытекает совпадение формул (4.27), определяющих взаимную информацию для непрерывного и дискретного случаев, если под f (х, у), f (х) и f (у) понимать обобщенные ф. п. в. дискретных с. в.

Дополнительным основанием для указанного выше определения взаимной информации служит следующее рассуждение, основанное на дискретизации непрерывных ансамблей и предельном переходе. Пусть (х, х + x) и (у, у + y) — интервалы на осях X и Y соответственно и

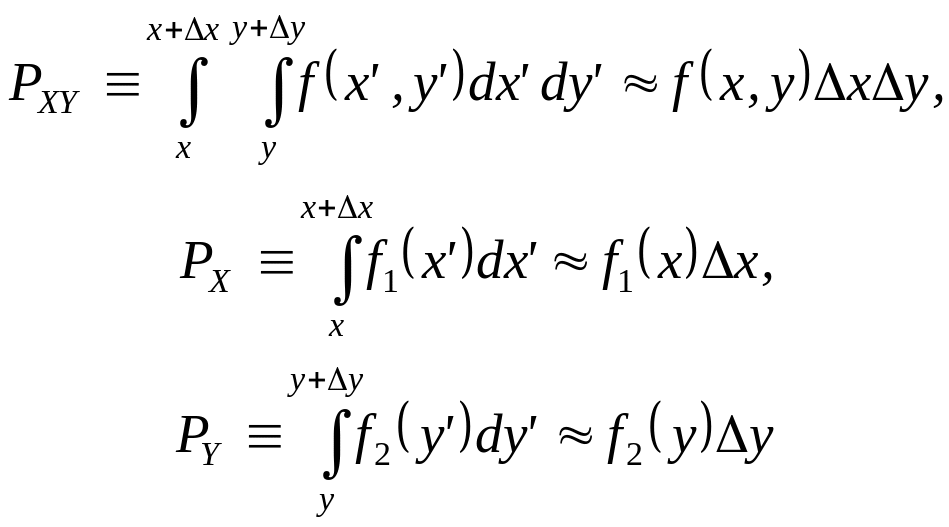(4.28)

— соответствующие этим интервалам вероятности. С каждым интервалом можно связать событие из некоторого дискретного множества. Так, предположим, что x_k и у_l — события, состоящие в том, что точка из X принадлежит интервалу (х, х + x) и точка из Y принадлежит интервалу (y, у + y) соответственно. Между событиями x_k и y_l определена взаимная информация

(4.29)

Устремляя x  0, y  0, получим

Этот предел и служит взаимной информацией между сообщениями (x, у) непрерывных ансамблей.

Рассмотрим теперь непрерывный ансамбль {XYZ, f (х, у, z)}. По аналогии с (4.27) можно определить условную информацию между парой сообщений х  X и у  Y при фиксированном сообщении z  Z

(4.30)

и информацию между парой сообщений (х, у)  XY и третьим сообщением z  Z

(4.31)

где условные и безусловные ф. п. в. определяются соотношениями, в которых суммы заменены на интегралы, а вероятности — на ф. п. в.

Каждое из количеств информации, определяемое соотношениями (4.27), (4.30) и (4.31), представляет собой случайную величину на соответствующем непрерывном ансамбле. Математическое ожидание

(4.32)

называется средней взаимной информацией между непрерывными ансамблями X и Y. Математическое ожидание

(4.33)

называется средней взаимной информацией между непрерывными ансамблями X и Y относительно сообщения z ансамбля Z. Математическое ожидание

(4.34)

называется средней взаимной информацией между непрерывными ансамблями X и Y относительно непрерывного ансамбля Z. Математическое ожидание

(4.35)

называется средней взаимной информацией между парой непрерывных ансамблей XY и непрерывным ансамблем Z.

Пример 2.4. Пусть f (х, у) — ф. п. в. двумерного гауссовского (нормального) закона распределения вероятностей на плоскости:

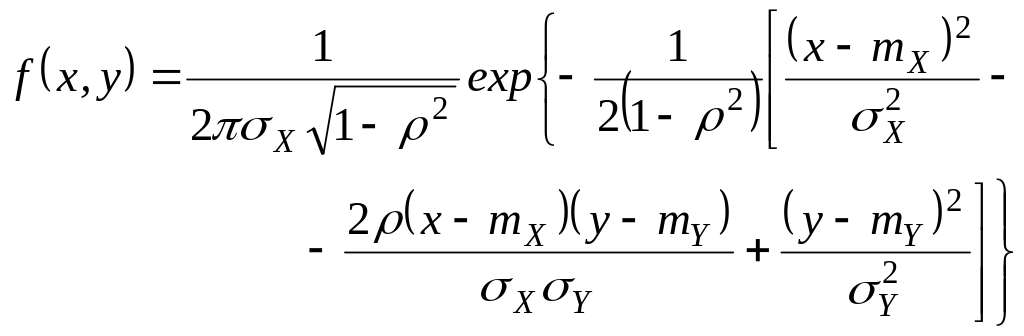(4.36)

Эта функция зависит от пяти параметров т_х, т_у, , и . Первые четыре параметра представляют собой математические ожидания и дисперсии соответствующих одномерных распределений, которые также являются гауссовскими:

(4.37)

(4.38)

Параметр  называется коэффициентом корреляции.

Для такого распределения вероятностей нетрудно вычислить величину средней взаимной информации. Используя в этом месте натуральные логарифмы и применяя формулу (4.32), получим

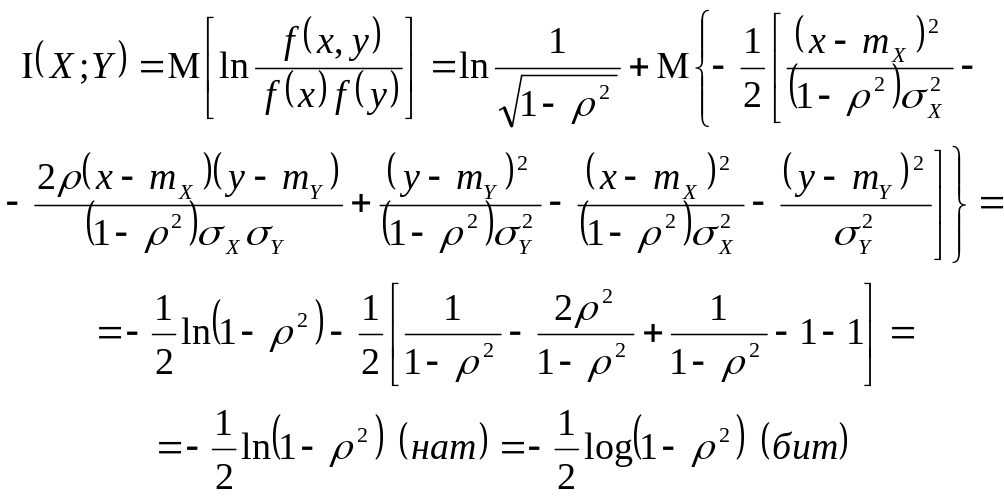(4.39)

где использованы определения диспепсии и коэффициента корреляции:

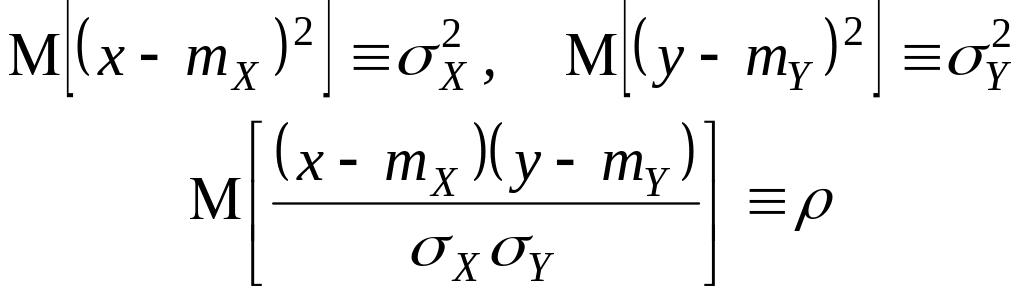(4.40)

Таким образом, средняя взаимная информация между двумя непрерывными совместно гауссовскими ансамблями (с. в.), имеющими коэффициент корреляции , определяется выражением

(4.41)

Во всех приведенных выше определениях средней взаимной информации (4.32)—(4.35) некоторые ансамбли могут быть непрерывными, а другие — дискретными. В этом случае приведенные формулы сохраняются, если ф. п. в. рассматривать как обобщенные ф. п. в. Возможно также представить эти формулы и в виде, использующем дискретные распределения. Для этого интеграл по соответствующей переменной должен быть заменен суммой, а ф.п.в. — выражениями вида (4.15), (4.16) с соответствующими обобщениями на случай более двух переменных. В качестве примера приведем формулу для средней взаимной информации I (X; Y | Z) для случая, когда X, Y — непрерывные ансамбли, а Z — дискретный:

(4.42)

Средняя взаимная информация между непрерывными или между непрерывными и дискретными ансамблями обладает многими из свойств, которые были раньше сформулированы для случая дискретных ансамблей.

4.2. Относительная энтропия и ее свойства

Практически все свойства средней взаимной информации являются общими для дискретных и непрерывных ансамблей. Эта общность является следствием того, что и дискретный и непрерывный случаи являются частными в общей абстрактной схеме введения информационной меры на измеримых вероятностных пространствах. Единственное отличие состоит в том, что для непрерывных ансамблей не определена собственная информация сообщений и, как следствие, не определена энтропия.

Однако можно ввести некоторые аналоги энтропии и в непрерывном случае и получить представление, похожее на (2.20). Рассмотрим среднюю взаимную информацию (4.32) между непрерывными ансамблями X и Y. Используя условные функции плотности вероятностей, можно записать

(4.43)

Если обозначить

(4.44)

то, используя (4.7), получим, что

I (X; Y) = H₀ (X) - H₀ (X | Y) = H₀ (Y) - H₀ (Y | X) (4.45)

Величины H₀ (), если существуют соответствующие интегралы, называются относительными (или дифференциальными) энтропиями непрерывных ансамблей. Они имеют много общих свойств с энтропиями дискретных ансамблей.

Первое свойство, отличающее относительную энтропию от энтропии дискретных ансамблей, состоит в том, что она может принимать различные по знаку значения. Это будет показано с помощью следующих примеров, в которых вычислена относительная энтропия для некоторых простых распределений вероятностей.

Пример 4.6. Пусть f (х) — ф. п. в. равномерного на отрезке (a, b) распределения:

Для ансамбля с таким распределением относительная энтропия H₀ (X) = log (b — а). Она принимает отрицательные значения, если (b — а) <1.

Пример 4.7. Пусть f (х) — ф. п. в. гауссовского распределения вероятностей с нулевым средним и дисперсией ²:

(4.46)

Тогда

(4.47)

где использовано условие нормировки , а также то, что математическое ожидание равно нулю и, следовательно,

.

Пусть {XY, f (x, у)} — непрерывный ансамбль, образованный парой совместно заданных непрерывных ансамблей {X, f (x)} и {Y, f(у)}. Величина

(4.48)

называется относительной энтропией ансамбля XY. Представляя f (х, у) в виде произведения условной и безусловной ф. п. в., получим

H₀ (XY) = H₀ (X) + H₀ (Y | X) = H₀ (Y) + H₀ (X | Y), (4.49)

т. е. относительная энтропия обладает свойством аддитивности.

Если {X₁,...,X_n, f(x)} совместно заданные п непрерывных ансамблей х = (x⁽¹⁾,..., x⁽ⁿ⁾), x⁽ⁱ⁾  X_i, i = 1, ..., n, то, используя соотношение f (x) = f (x⁽¹⁾) f (x⁽²⁾ | х⁽¹⁾) ... f (x⁽ⁿ⁾ | x⁽¹⁾,..., x^(n1)), получим

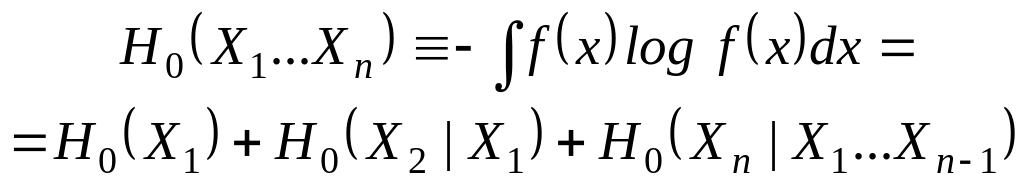(4.50)

С помощью неравенства для логарифма легко доказывается, что для непрерывных ансамблей X и Y

H₀ (Y | X)  H₀ (Y) (4.51)

с равенством в том и только том случае, когда ансамбли X и Y статистически независимы, т. е. когда выполняется соотношение (4.10).

Рассмотрим один важный частный случай, когда выражение для условной относительной энтропии можно упростить. Пусть X и Y — две случайные величины, связанные равенством Y = X + Z, где с. в. Z статистически не зависит от X. Обозначим через f_Z () ф. п. в. этой с. в. Тогда, как нетрудно увидеть,

f ( y | x ) = f_Z ( y – x ). (4.52)

Действительно, левая часть это ф.п.в. с.в. Y при фиксированном значении X = х. Так как при этом с. в. Y и Z отличаются только математическим ожиданием (математическое ожидание Y равно математическому ожиданию Z плюс х), то имеет место (4.54). Отсюда следует, что при любом x  X

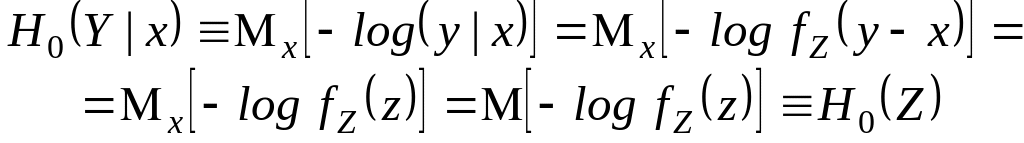(4.53)

где третье равенство — результат замены переменных, а четвертое — следствие независимости X и Z. Усредняя обе части (4.53) по всем x, получим, что для рассматриваемых с. в.

(4.54)

Относительная энтропия определяется распределением вероятностей на ансамбле, и естественным является вопрос о том для каких распределений она больше. Однако такой вопрос без дополнительных ограничивающих предположений лишен смысла поскольку, как видно, например, из (4.46) или (4.47), относительная энтропия может быть сделана сколь угодно большой либо соответствующим выбором интервала (а, b) в первом случае, либо выбором параметра ² во втором.

Пусть  — такой класс ф. п. в. на числовой прямой, что для каждой функции f(x)  выполняется условие

(4.55)

Слева в этом неравенстве написан второй начальный момент распределения с ф. п. в. f (х). Он называется средней мощностью с. в., ф. п. в. которой есть f (x). Название связано с тем, что в случае, когда х есть напряжение, то x² есть мощность в единичном сопротивлении. Таким образом,  — множество ф. п. в. для с. в. со средней мощностью, ограниченной числом с².

Т е о р е м а . Для любой ф. п. в. f (х)   выполняется неравенство

(4.56)

где H₀ (X) — относительная энтропия ансамбля {X, f (x)}. Равенство имеет место в том случае, когда

(4.57)

т. е. когда распределение вероятностей является гауссовским и имеет нулевое среднее и дисперсию с².

Докажем вначале вспомогательное неравенство. Пусть f (х) — произвольная функция из , тогда

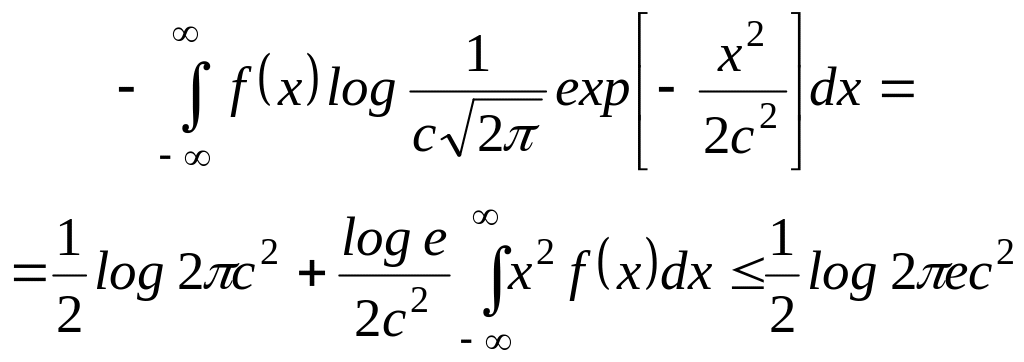(4.58)

Из этого неравенства следует, что

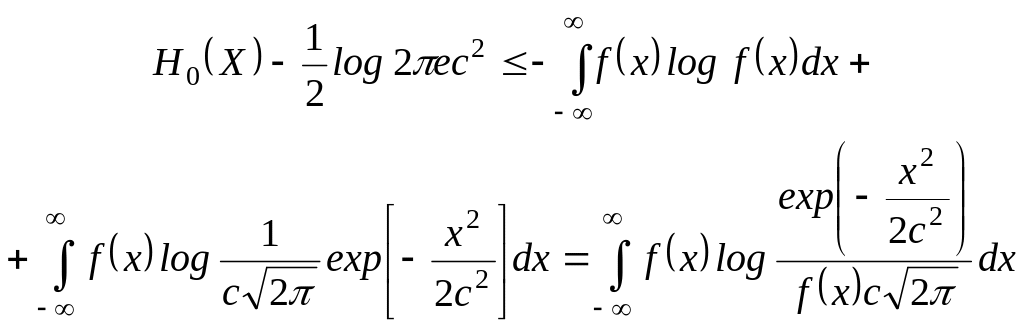
Отсюда, применяя неравенство для логарифма, получим

(4.59)

где последнее равенство следует из того, что каждое из выражений в квадратных скобках равно единице. Таким образом, получено неравенство (4.56). Случай равенства получается, когда имеет место равенство в неравенстве для логарифма, т. е. когда ф. п. в. определяется формулой (4.57). Теорема доказана.

Таким образом, мы показали, что среди всех случайных величин с ограниченным средним квадратом наибольшей относительной энтропией обладает гауссовская случайная величина. То, что эта случайная величина имеет нулевое математическое ожидание, не является существенным требованием. Легко показать, что случайные величины, отличающиеся только математическим ожиданием, имеют одинаковые относительные энтропии. Поэтому упоминание в теореме о том, что математическое ожидание равно нулю, можно опустить.

Рассмотрим теперь относительную энтропию системы случайных величин Х₁, ..., Х_п с совместной ф. п. в. f (х⁽¹⁾,..., х⁽ⁿ⁾). Обозначим через m₁,...,m_n математические ожидания этих величин:

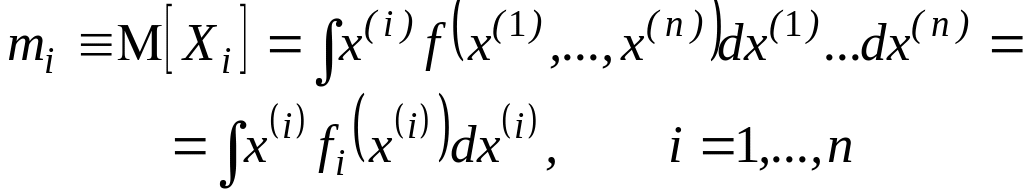(4.60)

где функции f_i (х⁽ⁱ⁾), i = 1, ..., п, определяются соотношениями (4.9). Обозначим через К_ij корреляционный момент с. в. X_i и Х_j:

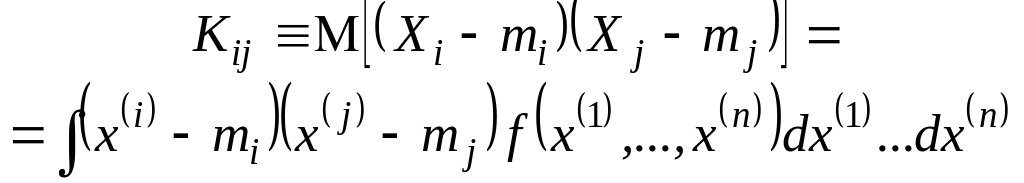(4.61)

Матрица К = [К_ij], i, j = 1, ..., n, элементами которой являются корреляционные моменты К_ij, называется корреляционной матрицей системы с. в. Х₁,..., Х_п.

Относительная энтропия системы с. в. Х₁,..., Х_n определяется соотношением

(4.62)

где f (х) = f (x⁽¹⁾,..., х⁽ⁿ⁾). B п-мерном случае сохраняется свойство экстремальности гауссовского распределения вероятностей по отношению к относительной энтропии.

Обозначим через K^1 матрицу, обратную матрице K, т. е. такую, что

K^1 K = I_n, (4.63)

где I_n — единичная матрица порядка п. Обратная матрица K^1 всегда существует, если матрица K обладает ненулевым определителем, что в дальнейшем и будет предполагаться:

det K  0 (4.64)

Так как К_ij = К_ji, то матрица K и, как нетрудно доказать, матрица K^1 являются симметрическими. Из определения обратной матрицы и определения матричного умножения следует, что

(4.65)

где — элементы матрицы K^1, а отсюда и из симметричности матрицы K следует, что

(4.66)

Функция

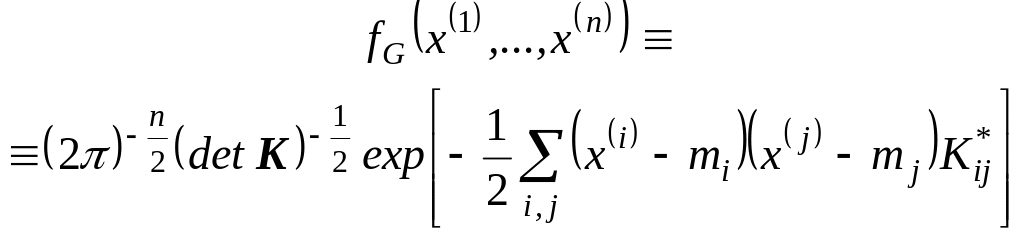(4.67)

называется ф.п.в. n-мерного невырожденного гауссовского распределения вероятностей. Если с. в. Х₁, ..., Х_п имеют ф. п. в. (4.67), то эти с. в. называются совместно гауссовскими. Можно показать, что в этом случае каждая из с. в. системы также имеет гауссовское распределение вероятностей.

Т е о р е м а . Пусть _п — класс ф.п.в. п c.в. заданными значениями математических ожиданий m₁, ..., т_n и заданной корреляционной матрицей K, det К  0. Для любой функции f (x)  _п; выполняется неравенство

(4.68)

причем равенство имеет место в том случае, когда f (х) есть ф.п.в. п-мерного гауссовского распределения вероятностей с математическими ожиданиями m₁, ..., т_п и корреляционной матрицей K, т. е. когда f (х) = f_G (х).

Докажем вначале вспомогательное равенство. Пусть f (х) — произвольная функция из _п, тогда

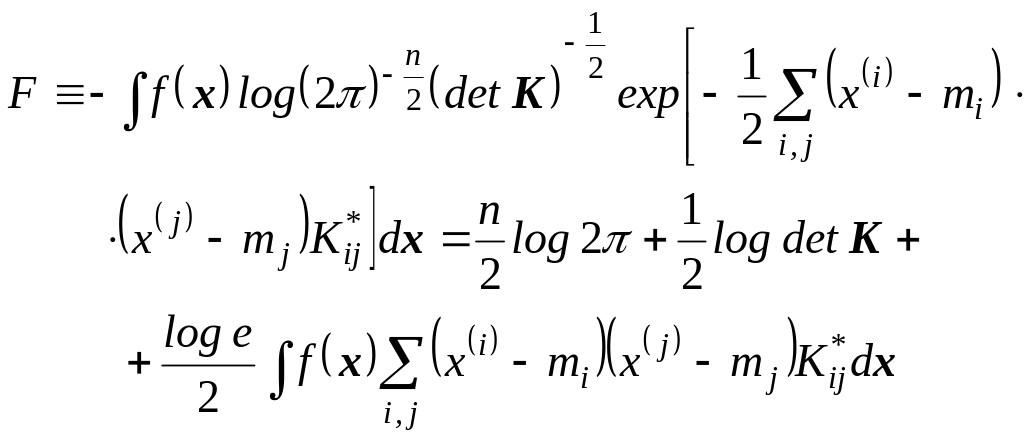(4.69)

Очевидно (см. (4.61) и (4.66)), что

(4.70)

откуда

(4.71)

Используя это равенство и неравенство для логарифма, получим

(4.72)

что и доказывает теорему.

Как и в одномерном случае, легко доказать, что относительная энтропия системы с. в. не зависит от математических ожиданий, поэтому упоминание о математических ожиданиях в теореме можно опустить.

Пример 4.8. Здесь мы дадим пример использования теоремы для вычисления средней взаимной информации между двумя гауссовскими случайными векторами. Пусть X = (Х₁, ..., Х_п) — вектор, образованный системой гауссовских с. в, Х₁, ..., Х_п с нулевыми средними и корреляционной матрицей К_X. Пусть Z =(Z₁, ..., Z_n) — такой же вектор с корреляционной матрицей К_Z, det К_Z  0; будем считать, что векторы X и Z статистически независимы. Нас интересует средняя взаимная информация I (Х; Y) между векторами X и Y = X + Z. Как было показано выше,

I (Х; Y) = H₀ ( Y ) - H₀ ( Y | X ) (4.73)

Так как Y — гауссовский вектор и корреляционная матрица этого вектора

К_Y=(М[Y_i Y_j])=(M[X_i + Z_i)(X_j + Z_j)])= =(М [X_i X_j])+(М [Z_i Z_j])=К_X +K_Z (4.74)

где третье равенство есть следствие независимости векторов X и Z, то det (К_X + К_Z)  0 и

(4.75)

Условная относительная энтропия H₀ (Y | X) = H₀ (Z), поскольку f (y | х) = f_Z (у — х), где f_Z (•) — ф. п. в. вектора Z. Аргументация здесь в точности такая же, как и при получении соотношения (4.56). Следовательно,

(4.76)

(4.77)

4.3. Непрерывные каналы с дискретным временем. Обратная теорема кодирования

Пусть множества X и Y сигналов на входе и выходе соответственно непрерывного канала с дискретным временем — числовые оси. Передача одного сигнала х  X (однократная передача) в некоторой фиксированный момент времени задается с помощью условной (или переходной) функции плотности вероятностей (ф. п. в.) f (у | х), у  Y. Передача последовательностей задается с помощью условных (или переходных) многомерных ф.п.в. в точности так же, как задается передача последовательностей по дискретному каналу. Мы будем считать, что передача сообщений начинается в момент времени i = 1, поэтому непрерывный канал с дискретным временем считается заданным, если для любого п = 1, 2, ... и любых последовательностей х = (х⁽¹⁾, ..., х^(п))  Х^п, у = (y⁽¹⁾, ..., у^(п))  Yⁿ заданы n-мерные ф. п. в. f (у | х), описывающие передачу последовательностей длины п в таком канале.

Непрерывный канал с дискретным временем называется каналом без памяти, если для всех п = 1, 2, ..., х  Х^п, у  Yⁿ,

(4.78)

Если, кроме того, ф.п.в., задающие передачу в моменты времени i и j, одинаковы для всех i и j, т. е. если

(4.79)

то говорят, что канал с дискретным временем удовлетворяет условию стационарности. В дальнейшем мы всегда будем предполагать, если противное не оговорено особо, что условие стационарности всегда выполняется.

В случае дискретного канала максимум средней взаимной информации на сообщение по всем распределениям вероятностей на входе давал пропускную способность канала, т. е. наибольшую скорость передачи, при которой вероятность ошибки могла быть сделана сколь угодно малой. В случае непрерывного канала это не так. Средняя взаимная информация может быть сделана какой угодно большой соответствующим выбором распределения вероятностей на входе. В этом основное отличие дискретных и непрерывных каналов. Следующий пример поясняет суть этого явления; он также подсказывает правильную постановку задачи кодирования.

Пример 4.8. Пусть X, Y, Z — гауссовские случайные величины (с. в ) связанные следующим соотношением: Y = X + Z, причем X и Z статистически независимы. Можно рассматривать X как входной и Y как выходной сигналы канала в некоторый момент времени. Величина Z называется шумом, а соответствующий канал — канал с аддитивным гауссовским шумом. Мы рассматриваем случай, когда распределение на входе канала является гауссовским В этом случае

(4.80)

где и | — дисперсии (мощности) сигнала на входе канала и шума. Очевидно, что = +

Средняя взаимная информация I(X; Y) может быть представлена как разность относительных энтропии

I (X; Y) = H₀ ( Y ) — H₀ ( Y | X) (4.81)

Из свойств относительной энтропии следует, что

(4.82)

(4.83)

Где

(4.84)

и, следовательно,

(4.85)

Используя (4.81), (4.82) и (4.85), получим, что

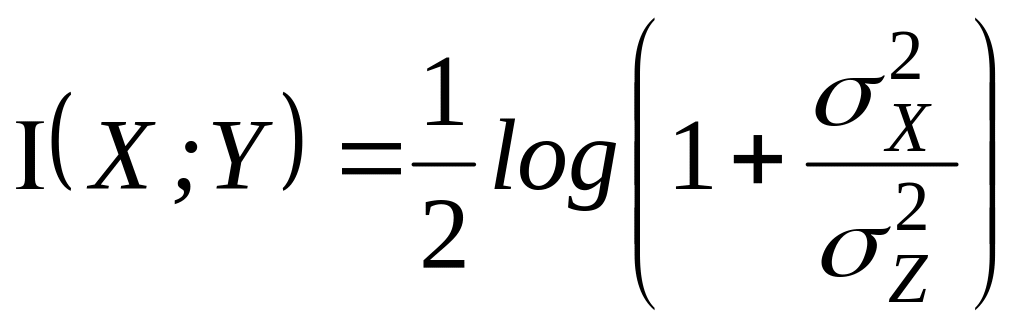(4.86)

Из этого выражения видно, что средняя взаимная информация между входными и выходными сигналами канала в некоторый момент времени может быть сделана сколь угодно большой за счет выбора достаточно большого отношения / . Если канал задан, то задана и мощность шума , поэтому, выбирая мощность входных сигналов достаточно большой, можно получить сколь угодно большое значение I (X; Y).

На практике входным сигналам нельзя придавать сколь угодно большую мощность, так как мощность передатчика ограничена. Поэтому входные сигналы непрерывных каналов, а, следовательно, и распределения вероятностей на входе канала должны подчиняться так называемым мощностным ограничениям.

Пусть и₁, ..., и_M — последовательности длины п (кодовые слова), образованные входными сигналами канала (и_i = ( )  Хⁿ, i = 1, .... М), и А₁, ..., А_M -непересекающиеся подмножества (решающие области), образованные выходными сигналами канала, A_i  Yⁿ, i = 1, ..., М. Кодом для непрерывного канала с дискретным временем, удовлетворяющим ограничению Р на среднюю мощность, будем называть множество пар {и₁, A₁; ...; и_M, А_M}, такое, что

(4.87)

для каждого кодового слова u_i. Число

(4.88)

называется скоростью, а число п — длиной кода. Так же как в дискретном случае, код для непрерывного канала будет обозначаться символом G (n, R).

Набор решающих областей задает правило декодирования: если выходная последовательность у канала принадлежит множеству А_i, то принимается решение о том, что передавалось кодовое слово и_i. Если при передаче и_i последовательность у не принадлежит А_i, то происходит ошибка. Вероятность этого события определяется соотношением

(4.89)

Как и в случае дискретных каналов, для каждого кода определены максимальная  и средняя  вероятности ошибок.

Пропускной способностью непрерывного канала с дискретным временем при ограничении Р на среднюю мощность входных сигналов называется максимальное число С такое, что для любого сколь угодно малого положительного  и любого R < С существует код G (n, R), все слова которого удовлетворяют ограничению (4.87) и максимальная вероятность ошибки которого удовлетворяет неравенству   .

Введем теперь понятие информационной емкости непрерывного канала с дискретным временем при ограничении на среднюю мощность входных сигналов. Для этого рассмотрим всевозможные ф. п. в. на Х^п. Обозначим через Ф_п (Р) множество всех ф. п. в. на Х^п таких, что

(4.90)

где

(4.91)

и

(4.92)

Информационной емкостью непрерывного канала с дискретным временем при ограничении Р на среднюю мощность входных сигналов называется число С^*, определяемое следующим соотношением:

(4.93)

где верхняя грань разыскивается по всем п и по всем ф. п. в. f (х)  Ф_п (Р), a I (Хⁿ; Yⁿ) — средняя взаимная информация, вычисленная для данного канала и для ф. п. в. f (х)  Ф_п (Р).

Понятие информационной емкости позволяет сформулировать и доказать обратную теорему кодирования. В основе доказательства обратной теоремы лежит неравенство Фано, которое справедливо для произвольного канала. Заметим, что в случае непрерывных каналов с дискретным временем условные вероятности р (w_j | u_i) принятия решения w_j при условии, что передано кодовое слово u_i, i = 1, ..., М, вычисляются следующим образом:

(4.94)

Т е о р е м а (обратная теорема кодирования для непрерывных каналов с дискретным временем при ограничении на среднюю мощность сигналов на входе). Пусть С^* — информационная емкость указанного выше канала при ограничении Р на среднюю мощность сигналов на входе. Пусть  — произвольное положительное число и R = С^* + . Тогда найдется такое положительное число , зависящее от R, что для всякого кода G (п, R), удовлетворяющего ограничению Р на среднюю мощность, средняя вероятность ошибки   .

Зафиксируем п и рассмотрим некоторый код G (п, R) при R = С^* + ,  > 0, все слова которого удовлетворяют условию (4.87). Обозначим через u₁, ..., и_M слова этого кода и положим

\

(4.95)

где  (х) — дельта-функция Дирака (если х = (х⁽¹⁾,…, х^(п)), то ). Функция f (x) является обобщенной ф. п. в. дискретного распределения на X^п, приписывающего одинаковые вероятности 1/М всем кодовым словам и нулевые вероятности всем остальным последовательностям из Х^п. Легко проверить, что функция f (х) принадлежит Ф_n (Р). Для того чтобы в этом убедиться, заметим, что неравенство (4.87) можно записать в следующей векторной форме:

(4.96)

где «т» — символ транспонирования вектора и_i. Рассмотрим левую часть неравенства (4.90). Очевидно,

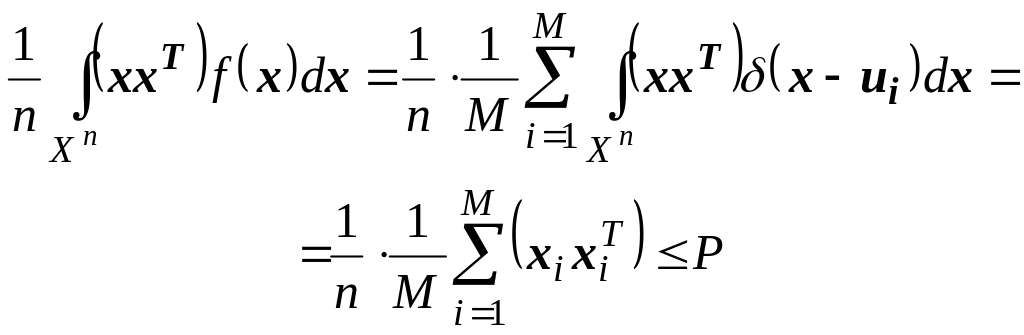(4.97)

т. е. для ф. п. в. (4.95) неравенство (4.90) выполняется.

Из определения информационной емкости (4.93) следует, что для ф. п. в. (4.95) выполняется следующая цепочка неравенств:

(4.98)

где U — ансамбль кодовых слов с равномерным распределением вероятностей, W — ансамбль решений, и последнее неравенство есть следствие невозрастания средней взаимной информации при преобразованиях. Доказательство теоремы завершается применением неравенства Фано и рассуждений, приведенных при доказательстве обратной теоремы кодирования для дискретных каналов. Теорема доказана.

4.4. Кодирование источников с заданным критерием качества.

Ранее требовалось определить наименьшее количество кодовых символов на сообщение источника, при котором сообщения возможно восстановить точно или со сколь угодно малой вероятностью ошибки по выходной последовательности кодера. Теперь не будем требовать точного или сколь угодно точного восстановления. Мы введем понятие критерия качества и ошибки восстановления, связанной с этим критерием качества, и потребуем, чтобы восстановление осуществлялось с ошибкой, не превосходящей заданное значение. Вопрос, который при этом будет нас интересовать, по-прежнему заключается в определении наименьшего количества кодовых символов на сообщение источника или наименьшей достижимой скорости кодирования, при которой такое восстановление можно осуществить.

Задача кодирования при заданном критерии качества естественно возникает при кодировании непрерывных источников. Действительно, всякий прибор, измеряющий сигналы на выходе непрерывных источников, обязательно вносит ошибки измерений. С другой стороны, если такой источник сопрягается с вычислительной машиной или цифровым вычислительным устройством, то его сообщения могут быть обработаны только с некоторой ошибкой, связанной с дискретностью устройства. Очевидно, что ошибка может быть сделана тем меньшей, чем больше символов некоторого алфавита, например, чем больше десятичных символов используется для представления одного сообщения непрерывного источника. Задача заключается в том, чтобы установить минимальное количество символов на сообщение, при котором величина ошибки не превосходит заданное значение.

При кодировании дискретных источников также можно представить себе ситуацию, в которой возникает задача кодирования с заданным критерием качества. Предположим, что с точки зрения некоторого получателя сообщения источника избыточны и ему достаточно иметь только какую-то часть из них. Пусть, например, дискретный датчик давления в кабине космического корабля измеряет давление с точностью 5 мм рт. ст. и каждое измерение имеет форму семиразрядного двоичного числа. Пусть также имеется контролирующая система, которая должна срабатывать, когда давление выйдет из допустимых пределов. С точки зрения получателя, которым является эта система, измеренные значения давления избыточны. Можно ввести критерий качества, адекватный задаче контроля, и задаться вопросом о том, какое количество двоичных символов в этом случае необходимо. Понятно, что это количество будет существенно меньшим, чем семь двоичных символов.

Другой важный случай, когда возникает задача кодирования с критерием качества, связан с передачей сообщений по каналам связи. Предположим, что сообщения некоторого источника передаются по каналу связи. Если в канале есть шум, то, как было показано в предыдущих главах, возможно так закодировать передаваемые сообщения, чтобы при декодировании ошибки появлялись бы со сколь угодно малой вероятностью, т. е. так, чтобы шум в канале практически не влиял бы на передачу сообщений. Единственное требование, которое должно быть при этом удовлетворено, состоит в том, чтобы количество информации, подаваемое в единицу времени на вход канала, не было слишком большим, точнее, чтоб'ы оно не превосходило константы С, определяемой каналом и называемой пропускной способностью канала. Пусть Н есть количество информации в единицу времени, порождаемое источником. Если Н < С, то возможно передать сообщения источника через канал так, чтобы они восстанавливались со сколь угодно малой вероятностью ошибки. Но если Н > С, то этого сделать нельзя и при декодировании почти всегда будут возникать ошибки.

Если теперь ввести критерий качества и в соответствии с ним определять численное значение ошибки, то можно поставить вопрос о том, какова наименьшая достижимая ошибка, возникающая при передаче сообщений данного источника по данному каналу. Нетрудно понять, что ошибка связана с количеством информации H, порождаемым источником. Если обозначить через Н () количество информации в единицу времени при ошибке , то наименьшая достижимая ошибка будет равна корню уравнения Н () = С.

4.4.1. Критерии качества. Постановка задачи кодирования с заданным критерием качества

Пусть источник U_X в каждый момент времени выбирает сообщение из множества X, которое может быть как дискретным, так и непрерывным, и Х^п — множество последовательностей сообщений х = (х⁽¹⁾, ..., x⁽ⁿ⁾), которые порождает этот источник за n последовательных моментов времени. Предположим, что последовательность сообщений (x⁽¹⁾, . . ., х^(п)) должна быть представлена с помощью аппроксимирующей последовательности у = (y⁽¹⁾, ..., y⁽ⁿ⁾) из элементов, вообще говоря, некоторого другого множества Y. Нас будет интересовать только такой случай, когда все, быть может бесконечное, множество Х^п последовательностей сообщений источника представляется с помощью конечного множества, содержащего М различных аппроксимирующих последовательностей у₁ , ..., у_M  Yⁿ,

Введем в рассмотрение функцию d_n (х, у), каждое значение которой будем считать величиной ошибки, возникающей при аппроксимации последовательности х с помощью последовательности у. Мы будем считать также, что

(4.99)

где d (х, у), х  X, у  Y, — некоторая неотрицательная функция, задающая величину ошибки и называемая критерием качества. Критерий качества задает величину ошибки при аппроксимации буквы х в последовательности х соответствующей буквой у в последовательности у и поэтому иногда называется побуквенным критерием качества. Для побуквенного критерия качества d_n (х, у) представляет собой среднюю величину из ошибок представления п компонент последовательности х. Мы будем предполагать, что d (х, у)  0 для всех х  X и у  Y.

Hас будут интересовать различные способы сопоставления последовательностей сообщений х  Х^п и аппроксимирующих последовательностей y_l, ..., у_M. Один из возможных способов — детерминированный. При появлении на выходе источника последовательностей х для аппроксимации используется вполне определенная последовательность у, которую можно обозначить через у (х). Имеется, вообще говоря, много (в непрерывном случае — бесконечно много) последовательностей х  Х^п, которые аппроксимируются с помощью одной и той же последовательности у, так что отображение у (х) не взаимно однозначно. В некоторых случаях удобно рассматривать случайный способ сопоставления, предполагая, что имеется некоторый вероятностный механизм аппроксимации, который описывается с помощью условных вероятностей р (у | х) использования последовательности у для аппроксимации последовательности х. Детерминированный способ аппроксимации также может быть описан с помощью условных вероятностей р (у | х), которые в этом случае задают вырожденное распределение, т. е.

(4.100)

Таким образом, вероятностная аппроксимация включает в себя как частный случай детерминированную.

При рассмотрении непрерывных источников аппроксимирующее множество Y, как правило, также непрерывно (представляет собой числовую ось). Поэтому случайную аппроксимацию задают с помощью функции плотности вероятностей f (у | х). Детерминированной аппроксимации при этом соответствует обобщенная ф. п. в

(4.101)

Пусть задан источник U_X. Это означает, что для любого п задано распределение вероятностей р (х), х  Х^п (в дискретном случае), или ф. п. в. f (х), х  Х^п (в непрерывном случае). Тогда для каждого условного распределения вероятностей р (у | х), х  Х^п, у  Yⁿ, или условной ф. п. в. f (у | х), х  Х^п, у  Yⁿ, задан ансамбль {XⁿYⁿ, р (х, у) = р (х) р (у | х)} (в дискретном случае) или ансамбль {XⁿYⁿ, f (х, у) = f (x) f (у | х)} (в непрерывном случае). Очевидно, что функция d_n (х, у) представляет собой случайную величину на ансамбле Х^пYⁿ. Ее математическое ожидание называется средней ошибкой

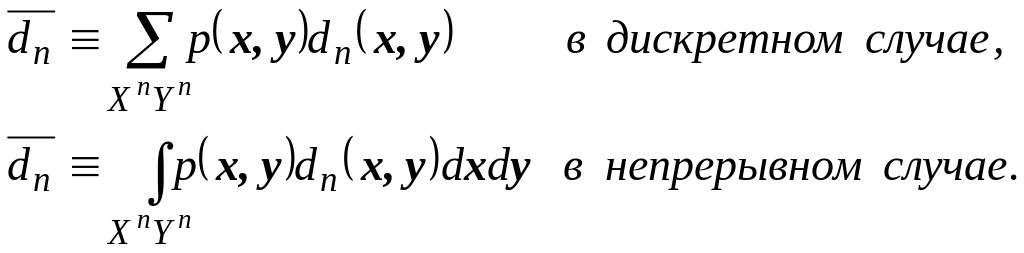(4.102)

Пусть X_iY_i — ансамбль пар сообщений (x⁽ⁱ⁾, y⁽ⁱ⁾), соответствующих моменту времени i, i = 1, 2, ..., п. Очевидно, что функция d (x⁽ⁱ⁾, y⁽ⁱ⁾) является случайной величиной на ансамбле Х_iY_i, ее математическое ожидание называется средней ошибкой аппроксимации i-й буквы. Так как математическое ожидание суммы равно сумме математических ожиданий, то из (4.102) следует, что

(4.103)

Пример 4.9. Пусть Х = Y = {a₁, ..., a_L} —два дискретных множества, состоящие из одного и того же набора элементов. Положим

(4.104)

Математическое ожидание с. в. d (x, у) на ансамбле XY

(4.105)

и

В этом случае средняя ошибка просто равна средней вероятности того, что символы в последовательностях х и у не будут совпадать. Такой критерий качества называется вероятностным.

Предположим, что L = 2, п = 3 и на множестве X = {0, 1} задано равномерное распределение вероятностей. Предположим также, что аппроксимирующее множество состоит из двух последовательностей у₁ = (000) и у₂ = (111). В соответствии с (4.99) и (4.105) величина d_n (x, у) равна относительному числу символов, в которых последовательности х и у не совпадают. Например,

d_n((010), (111)) = 2/3.

Рассмотрим неслучайное сопоставление элементов множества X³ и последовательностей у₁, у₂, при котором у (х) есть такая последовательность, которая минимизирует величину d_n (x, у). Это сопоставление приведено в следующей таблице.

Таблица 4

Последо-ватель-ность источни-ка х	Апроксими-рующая последова-тельность y(x)	Ошиб-ка dn (x, у)	Последо-ватель-ность источни-ка х	Апрокси-мирующая последова-тельность y(x)	Ошиб-ка dn (x, у)
000	000	0	100	000	1/3
001	000	1/3	101	111	1/3
010	000	1/3	110	111	1/3
011	111	1/3	111	111	0

Нетрудно найти, что средняя ошибка d₃ = ¹/₄. Каждая из аппроксимирующих последовательностей появляется с вероятностью ¹/₂ и, следовательно, энтропия ансамбля аппроксимирующих последовательностей равна 1. Это значит, что существует однозначно декодируемый двоичный код из двух слов, для которого требуется один двоичный символ на аппроксимирующую последовательность или один двоичный символ на три сообщения источника. При этом сообщения источника будут восстанавливаться со средней ошибкой ¹/₄.

Приведенный расчет показывает, что введение критерия качества и восстановление сообщений источника не точно, а с заданным уровнем ошибок, понижает по крайней мере в этом примере скорость кодирования. Заметим, что при точном восстановлении скорость равна 1 бит на сообщение, тогда как в рассматриваемом примере она равна ¹/₃ бит на сообщение.

Пример 5.1.2. Предположим, что множество X выбрано, как в предыдущем примере, а множество Y совпадает с X, но содержит дополнительный (L+ 1)-й элемент; обозначим его через а_о. Пусть

В этом случае сообщение а₀ можно трактовать как стирание. Если  существенно меньше 1, то эта функция качества соответствует случаю, когда ошибки существенно более нежелательны, чем стирания.

Пример 4.10. Пусть X и Y — числовые оси и сообщения источника представляют собой действительные случайные величины. Положим

d (x, у)  (х — y)² (4.106)

Такой критерий качества приемлем, если при аппроксимации особенно нежелательны большие ошибки. Математическое ожидание

M [d (x, у)]  M [(х — y)²] (4.107)

есть средний квадрат ошибки или дисперсия ошибки, если М [(X — Y)] = 0. Поэтому такой критерий качества называется квадратическим, а соответствующая средняя ошибка — среднеквадратической.

Пример 4.11. Ниже мы покажем, что критерий качества можно подобрать так, чтобы выделить интересующие получателя свойства сообщений. Пусть имеется цифровой датчик давления и каждое измерение имеет форму семиразрядного двоичного числа х = (х⁽⁰⁾,х⁽¹⁾, ..., х⁽⁶⁾), причем величина давления , где  — некоторый нормирующий коэффициент. Будем для простоты считать, что давление представляет собой случайную величину, которая выходит из допустимых пределов (F_H, F_B) с вероятностью р и остается в допустимых пределах с вероятностью q = 1 — р.

Введем критерий качества и закодируем сообщения в соответствии с этим критерием так, чтобы по выходной последовательности кодера можно было бы однозначно определить, выходила или нет измеряемая величина из допустимых пределов. Пусть каждое сообщение х аппроксимируется семиразрядным двоичным числом у = (y⁽⁰⁾, y⁽¹⁾, ..., y⁽⁶⁾). Положим и

(4.108)

и выберем аппроксимирующее множество из двух чисел y_l, у₂ таких, что у₁ —любое число интервала (F_H /, F_В /,), a y₂ — любое число вне этого интервала. Если в качестве аппроксимирующего выбирается число, минимизирующее d(x, у) при заданном х, то, очевидно, средняя ошибка d будет равна нулю. При этом интересующее получателя событие — выход давления из допустимых пределов — определяется по у однозначно. Очевидно, сообщение у₁ имеет вероятность q, а сообщение y₂ — вероятность р, поэтому энтропия аппроксимирующего ансамбля равна h (р). Из результатов первой главы следует, что h (р) есть минимальное количество двоичных символов на сообщение, которое позволяет кодировать данный источник относительно критерия качества (4.108) с нулевой ошибкой.

Теперь дадим основные определения, относящиеся к задаче Кодирования источников с заданным критерием качества.

Пусть X — множество сообщений источника и Y — множество аппроксимирующих символов. Пусть п — некоторое натуральное число — длина кодируемых сообщений, тогда Х^п — множество всех последовательностей сообщений длины п на выходе источника, a Yⁿ — множество всех возможных аппроксимирующих последовательностей. Критерий качества d (х, у), х  X, у  Y, определяет величину ошибки d_n (х, у) (см. (4.99)) аппроксимации последовательности х  Х ^п последовательностью y  Y ^п.

Кодом для кодирования с заданным критерием качества последовательностей сообщений длины п называется произвольное множество Т_п = {u_l, ..., и_M}  Yⁿ аппроксимирующих последовательностей. Кодированием для кода Т_п называется произвольное отображение и (х) множества Х^п на множество кодовых слов Т_п. Число

(4.109)

называется средней ошибкой кодирования относительно критерия качества d (х, у). Число

(4.110)

называется скоростью кода Т_п.

Очевидно, что средняя ошибка минимизируется при таком кодировании, при котором для каждой последовательности х  Х^п выбирается кодовое слово и (х)  Т_п, минимизирующее величину ошибки d_n (x, u_i), другими словами,

(4.111)

Кодирование, определяемое соотношением (4.111), будем называть оптимальным для данного кода Т_п и данного критерия качества d (х, у).

Из приведенного выше определения следует, что каждый код характеризуется двумя величинами: средней ошибкой и скоростью кодирования R. Скорость кодирования представляет собой количество двоичных символов на сообщение источника, при котором возможно аппроксимировать сообщения источника со средней ошибкой .

На рис. 4.4 показана структура кодера источника, на выходе которого появляется в среднем R двоичных символов на сообщение. На выходе источника U_X последовательно появляются сообщения из множества X. Эти сообщения разбиваются на блоки длины п, и каждый блок подвергается кодированию независимо от остальных блоков. Устройство, обозначенное на рисунке буквой A (аппроксиматор), каждому блоку х  Х^п, поданному на его вход, сопоставляет аппроксимирующую последовательность из множества Т_п в соответствии с правилом кодирования (4.111). Все кодовые слова множества Т_п занумерованы; каждому слову сопоставляется последовательность двоичных символов, обозначающая его номер. Устройство, обозначенное на рисунке буквой В, определяет номер слова и (х) в множестве Т_п и представляет этот номер в двоичной форме (⁽¹⁾),  ⁽²⁾, ...,  ^пR).

Заметим, что количество двоичных символов на выходе кодера в точности равно R только в том случае, когда nR есть целое число (или М есть некоторая целая степень двойки). Если это не так, то количество двоичных символов на сообщение равно R' = | nR | / n, где | х | — наименьшее целое, большее или равное х. При больших п величины R и R' близки (отличаются друг от друга не более чем на 1/n).

Обозначим символом (R, d) код источника со скоростью R и средней ошибкой d.

U_X

A

B

x u (₁,…, _nR)

Рис. 4.4. Структура кодера

Пусть X и Y — фиксированные множества и d (х, у) — функция, определенная на множестве XY. Пусть U_X — источник, выбирающий сообщения из множества X.  -скоростью создания информации источником U_X относительно критерия качества d (х, у) называется наименьшее число H_ такое, что для любого R > H_ найдется (R, d) код относительно того же критерия качества при d  .

Далее мы будем заниматься отысканием -скорости создания информации некоторыми источниками. Для того чтобы установить, что некоторое число H_ является скоростыо создания информации относительно критерия качества d (х, у), следует доказать два утверждения:

1. Для любого R > H_ найдется п и код со скоростью R, кодирующий последовательности сообщений длины п, для которого средняя ошибка относительно критерия качества d (х, у) не превосходит  (прямая теорема кодирования).

2. Для любого R < H_ для всех п и для всех кодов со скоростью R средняя ошибка относительно критерия качества d (х, у) превышает  (обратная теорема кодирования).

4.5. Эпсилон - энтропия и ее свойства

Ключевая роль в задаче определения -скорости создания информации принадлежит специальной функции, эпсилон-энтропии, которую мы формально введем и изучим ее свойства. Полезность этой функции проявится позже. Дело обстоит в точности так же, как в задаче определения скорости создания информации дискретным источником. Мы вначале ввели и изучили энтропию, а затем показали, что скорость создания информации равна энтропии.

Пусть U_Х — непрерывный стационарный источник, выбирающий сообщения из множества X. Предположим, что Y — аппроксимирующее множество и d (х, у) — критерий качества. Для каждого целого п, п = 1, 2, ..., определен ансамбль {Х^п, f (х)} последовательностей сообщений длины п, распределение вероятностей на котором задается посредством ф. п. в. f(x), x = (x⁽¹⁾, ..., x⁽ⁿ⁾)  Xⁿ. Удобно полагать, что Х^п = Х₁ ,..., Х_n, где X_i — ансамбль сообщений в момент времени i.

Пусть Yⁿ — множество аппроксимирующих последовательностей у = (у⁽¹⁾, ..., y⁽ⁿ⁾), y⁽ⁱ⁾  Y, и f (y|x), x  Xⁿ, — произвольное семейство условных ф. п. в. на Yⁿ. Если Yⁿ —дискретное множество или дискретное подмножество непрерывного множества, то ф. п. в. f (у|х) будем рассматривать как обобщенные ф. п. в. Эти ф. п. в. совместно с ф.п.в. f (х) задают ансамбль {XⁿYⁿ, f (х, у)}, где f (х, у) = f (x) f (y|x), и ансамбль {Yⁿ, f (y)}, где

(4.112)

Удобно полагать, что Yⁿ = Y₁ ... Y_n, где Y_i —ансамбль аппроксимирующих сообщений в момент времени i. Заметим, что в общем случае ф. п. в. f_i (х⁽ⁱ⁾, y⁽ⁱ⁾), задающая распределение вероятностей на ансамбле Х_iY_i, зависит от номера i.

Для ансамбля {XⁿYⁿ, f (x, y)} определены две величины. Одна из них — средняя взаимная информация I (Xⁿ; Yⁿ) между ансамблями Xⁿ и Yⁿ:

(4.113)

Другая — средняя ошибка аппроксимации:

(4.114)

где

(4.115)

Пусть Ф_п () есть класс всех ф. п. в. f (y|x) такой, что для каждой функции из этого класса средняя ошибка не превосходит :

(4.116)

Пусть

(4.117)

где минимум разыскивается по всем функциям f (у|х) из Ф_п (). Тогда функция от  ^:

(4.118)

где точная нижняя грань берется по всем п, п = 1, 2, ..., называется эпсилон-энтропией непрерывного стационарного источника U_X относительно критерия качества d (x, у).

Рассмотрим свойства функции Н ().

Первое очевидное свойство этой функции состоит в том, что она не отрицательна и определена только для неотрицательных значений . Неотрицательность Н () следует из неотрицательности средней взаимной информации.

Второе свойство, также достаточно очевидное, состоит в том, что Н () — невозрастающая функция. Действительно, если ₁ > ₂, то при всех п множество Ф_п (₁) содержит множество Ф_п (₂) и, следовательно, минимум по некоторому множеству не может быть больше, чем минимум по части этого множества. Таким образом, H (₁)  H (₂).

Следующее свойство сформулируем в виде теоремы.

Т е о р е ма. Пусть U_X — источник без памяти, т. е. такой, что для любых п и любых х  Х^п, х = (x⁽¹⁾, ..., x⁽ⁿ⁾),

(4.119)

где все сомножители в правой части образованы с помощью одной и той же функции f (х) — безусловной ф. п. в. на ансамбле X. Тогда

(4.120)

где Ф () — множество всех одномерных условных ф. п. в. таких, что для любой функции f (у|х)  Ф ()

(4.121)

Имеем

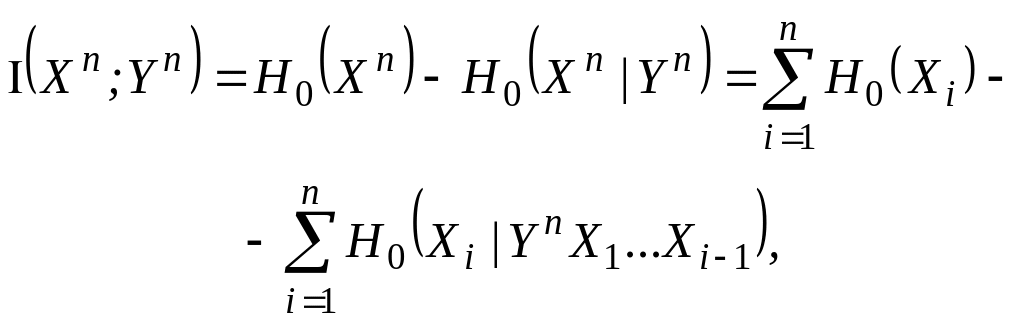(4.122)

где второе равенство является следствием независимости сообщений источника 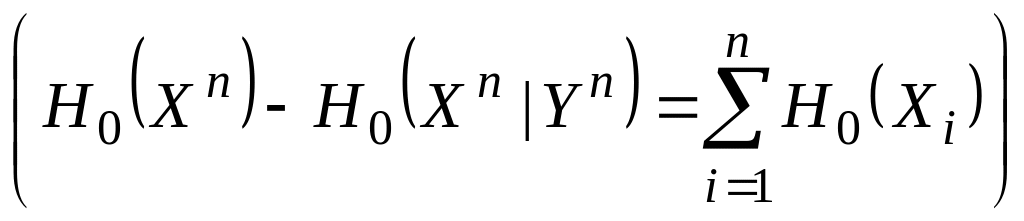и свойства аддитивности относительной энтропии. Далее, так как Yⁿ = Y₁ ... Y_n и относительная энтропия не уменьшается при исключении части условий, то для любого i, 1  i  п,

(4.123)

Поэтому

(4.124)

где использовано обозначение

и учтено то обстоятельство, что при всех i множества Х_iY_i совпадают между собой и с множеством XY. Индекс i в обозначении информации I_i (X; Y) означает, что она вычислена для ф. п. в. f_i (х, у) = f (х) f_i (у | х), которая для произвольной ф. п. в. f (у | х) может зависеть от индекса i. Если теперь положить ₁ = ... = _n = , то выражение в правой части (4.124) в силу выпуклости вниз средней взаимной информации по условным распределениям можно оценить следующим образом:

(4.125)

где I₀ (X; Y) — средняя взаимная информация, вычисленная для ф. п. в. f₀ (х, у) = f (x) f₀ (y | x), где

(4.126)

Из (4.114) следует, что f₀ (у | х)  Ф() для любой ф. п. в. f(y|x)Ф_n().

Заметим, что равенства в (4.125) и (4.124) достигаются, если выбрать

(4.127)

т.е. если пары (Х₁Y₁), ..., (X_nY_n) статистически независимы и одинаково распределены. Первое равенство является тогда следствием аддитивности информации, а второе — следствием того, что I_i (X; Y) = I₀ (X; Y) при всех i = 1, ..., п.

Покажем теперь, что функция f₀ (у | х) принадлежит множеству Ф(), если f₀ (у | х) принадлежит множеству Ф(). Для того чтобы в этом убедиться, достаточно увидеть, что при указанном выше выборе f₀ (y | x) средние ошибки будут одинаковы для всех i = 1, ..., п и равны . Но это так, поскольку пары (X_iY_i), i = 1, ..., п, одинаково распределены.

Таким образом, мы показали, что

(4.128)

Т е о р е м а . Эпсилон-энтропия Н () — выпуклая вниз функция .

Мы докажем эту теорему для случая источников без памяти и коротко обсудим общий случай. Для непрерывного источника без памяти

(4.129)

Предположим, что минимум в (4.129) для значений ₁ и ₂ достигается на условных ф. п. в. f₁ (у | х) и f₂ (y | x) соответственно. Пусть  — неотрицательное число, лежащее между нулем и единицей. Функция

(4.130)

есть ф. п. в., принадлежащая множеству Ф (₁+(1—)₂). Действительно, так как для функций f₁ (y | x) и f₂ (у | х) средние ошибки не превосходят величин ₁ и ₂ соответственно, то

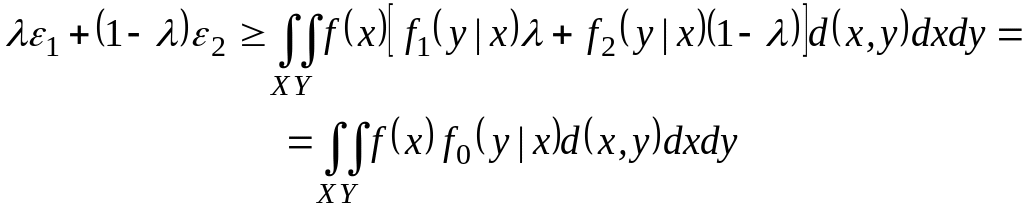(4.131)

Поэтому имеет место неравенство

(4.132)

где I₀(Х; Y) — средняя взаимная информация между ансамблями X и Y, вычисленная для функции f₀ (у|х). Теперь можно воспользоваться выпуклостью вниз средней взаимной информации по условным распределениям. Из выпуклости следует, что

I₀ (Х; Y)  I₁ (Х; Y) + (1) I₂ (Х; Y) = =H (_l) + (1 ) H (₂) (4.133)

где I_i (X; Y) — средняя взаимная информация, вычисленная для функции f_i (у | х).

Отсюда и из (4.132) вытекает выпуклость вниз функции Н ().

В общем случае в точности по той же схеме доказывается, что при каждом п функции Н_п () выпуклы вниз по . Выпуклость Н () следует из теоремы и из того, что предел последовательности выпуклых функций также является выпуклой в ту же сторону функцией. Теорема доказана.

Т е о р е м а . Пусть Н_п () ограничено при всех п = 1, 2,... Тогда последовательность {Н_п ()} имеет предел и

(4.134)

Эта теорема приводится без доказательства.

Теперь будет показано, что в некоторой области значений  эпсилон-энтропия Н () равна нулю. Пусть при некотором п

(4.135)

M_y есть условное математическое ожидание по ансамблю Х^п при условии, что у фиксировано. И пусть y  Yⁿ — элемент, на котором достигается этот минимум. Тогда Н_п () = 0 для всех   ₀ и, следовательно, H () = 0 при тех же значениях . Действительно, при выборе в качестве универсального аппроксимирующего элемента у₀ для всех х  Xⁿ средняя ошибка будет равна

(4.136)

Аппроксимации с помощью такого универсального элемента соответствует условная ф. п. в.

f (y | x) =  (y—y₀) для всех х  Х^п. (4.137)

Это означает, что ансамбли Xⁿ и Yⁿ статистически независимы и, следовательно, I (Xⁿ; Yⁿ) = 0 для ф. п. в. (4.137) Так как Н() не превышает 1/п I (Х^п | Yⁿ) = 0 и не отрицательно то H () = 0 для всех   ₀.

Пример 4.12. Рассмотрим квадратический критерий качества, введенный в примере 4.11. Пусть источник без памяти порождает случайные величины с нулевым математическим ожиданием . Число 0 является универсальным аппроксимирующим элементом при всех   D, где D —дисперсия величин на выходе источника. Действительно,

(4.138)

Эпсилон-энтропия такого источника равна 0 для всех   D.

Типичный график эпсилон-энтропии приведен на рис. 4.5.

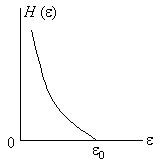
Рис. 4.5 Типичный график функции Н ()

5. Информационный подход к оценке качества функционирования систем связи

Под системой связи будем понимать совокупность технических средств, обеспечивающих передачу информации с заданными свойствами от различных источников различным получателям. Целенаправленная разработка системы связи может осуществляться при условии наличия критериев эффективности ее функционирования. Основной задачей системы связи является обеспечение максимальной скорости передачи при высоком качестве функционирования и экономичности системы.

Под качеством функционирования при этом понимается минимизация потерь информации, что в конечном итоге трансформируется в обеспечение высокой верности передачи.

Рассмотрим основные причины, приводящие к возможным потерям информации в системе связи. Они иллюстрируются схемой, представленной на рисунке 5.1.

На вход системы связи поступает поток сообщений, который далее может быть либо принят для передачи, либо не принят в связи с занятостью запоминающих или входных устройств системы связи. Поток сообщений, принятый для передачи, преобразуется в поток сигналов, предназначенных для передачи по каналу (будим полагать используемые в системе связи каналы дискретными и в качестве сигналов рассматривать последовательности символов кода). При этом преобразовании также могут возникать определенные потери информации, вызванные ненадежностью в основном кодирующих устройств и каналообразующей аппаратуры. Поток символов, поступивший из канала к приемнику может быть принят и не принят по причине неисправности аппаратуры или по причине ее занятости приемом других информационных потоков. Однако даже если поток был принят приемником, под действием помех в канале связи могут возникать такие ошибки, которые делают невозможным достоверное выявление информации. Последнее имеет место, если введенной в информацию избыточности оказалось недостаточно для исправления ошибок, возникших под действием помех в канале связи.

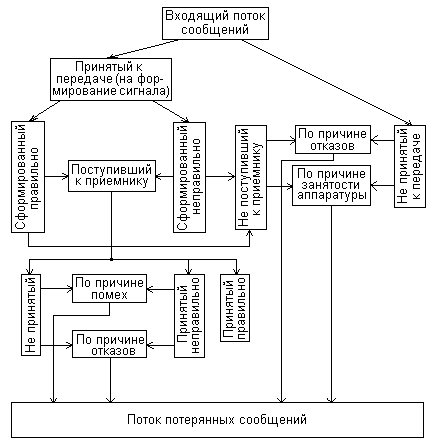
Рис.5.1. Основные причины, приводящие к возможным потерям информации в системе связи

Таким образом, из потока сообщений, поступающих на входы системы связи, формируется некоторый поток потерянных сообщений. Независимо от места возникновения потерь информации основными причинами потерь являются помехи в каналах связи, неисправность аппаратуры и перегрузка обслуживающих или запоминающих устройств.

Количественная оценка каждого из этих явлений может быть осуществлена с помощью теории вероятностей. Данное обстоятельство и позволяет сформировать единый информационный подход (т.е. подход с позиций теории информации) к оценке качества функционирования системы связи.

Для выяснения существа этого подхода рассмотрим подробнее все перечисленные составляющие потерь и их взаимодействие. Способность системы обеспечивать передачу информации с заданной верностью при воздействии помех в канале связи называют помехоустойчивостью.

Мешающее действие помех в дискретных каналах обычно оценивается некоторой моделью ошибок (в простейшем случае симметрично канала без памяти - вероятностью ошибки Р_ош). Эффективным средством борьбы с этим фактором является введение избыточности в передаваемый сигнал, которую называют информационной избыточностью. Существует два типа избыточности: кодовая избыточность и избыточность повторения. Под кодовой информационной избыточностью понимают наличие дополнительных, не несущих информации о существе передаваемого сообщения, разрядов в кодовой комбинации.

Для повышения качества функционирования технических средств можно использовать многократное повторение однотипных блоков, сигналов и т.п., для получения требуемой помехоустойчивости или надежности. Такую избыточность называют избыточностью повторения. Информационная избыточность повторения предполагает повторение информации в канале связи во времени, или повторение по временным или частотным каналам.

Наличие неисправности в аппаратуре приводит к ее неработоспособности. Под надежностью любой информационной системы понимают свойство системы выполнять свои функции "сохраняя во времени значения установленных эксплуатационных показателей в заданных пределах" (ГОСТ 13377-75). При оценке качества системы связи необходимо учитывать возможность возникновения сбоев и отказов. Под сбоем обычно понимается самоустраняющийся отказ, приводящий к кратковременному нарушению работоспособности. Под отказом понимают нарушение работоспособности аппаратуры.

Проблема надежности отличается от проблемы помехоустойчивости тем, что в случае отказа повторение одной и той же операции во времени не позволит обнаружить и исправить ошибку. Вместе с тем в системах с последовательными кодами одиночный отказ элемента может привести к неодиночной ошибке в выходном сигнале. Однако при соответствующем проектировании информационных систем основные методы обеспечения помехоустойчивой передачи информации могут быть применены к задаче конструирования надежных технических устройств. Также как и для повышения помехоустойчивости, для увеличения надежности необходимо вводить избыточность. В частности, с небольшими изменениями можно использовать большинство результатов теории кодирования при введении аппаратурной кодовой избыточности.

Проблема помехоустойчивости в определенной степени является противоречивой по отношению к проблеме надежности. Если для увеличения помехоустойчивости необходимо увеличивать избыточность передаваемой информации, то это приводит к усложнению системы и если вводимая избыточность не рассчитывалась на исправление ошибок, возникших из-за неисправности аппаратуры, то снижается надежность. Только оценивая помехоустойчивость и надежность единым критерием, можно оценить общую эффективность построения системы связи. Свойство системы в отношении помехоустойчивости и надежности можно связать с количеством информации, проходящим через систему.

Представим обобщенно мешающие воздействия в виде некоторых условных канала с шумом отказов аппаратуры и канала с шумом помех в линии связи (рисунок 5.2).

Рис.5.2. Обобщенно мешающие воздействия в виде некоторых условных канала с шумом отказов аппаратуры и канала с шумом помех в линии связи

Это соответствует выделению идеальной системы без потерь информации и последовательно соединенных с ней каналов с шумом отказов и помех. Объединим оба последних канала в единый канал с шумом (рисунок 5.3).

Рис.5.3. Канал с шумом

В соответствии с количеством информации, передаваемое через такой канал

I(Z,U)=H(Z)-H(Z/U),

где H(Z)-энтропия на выходе канала, H(Z/U) - условная энтропия приема ансамбля сообщений Z при условии наличия на входе канала ансамбля сообщений U.

Величину H(Z/U) можно определить, если с учетом имеющих место в канале помех и конкретной конфигурации аппаратной реализации системы определить вероятность потерь Р₀, вызванных ошибками выявления сообщения, возникающей из-за помех и отказов.

Однако для получения общей вероятности потерь в системе необходимо учесть еще потери, вызванные отказом в обслуживании. Расчет вероятности потерь по причине отказа в обслуживании можно вести исходя из известных в теории массового обслуживания соотношений.

Снижение этих потерь также может быть осуществлено путем введения избыточности в обслуживании. Она позволяет уменьшать время обслуживания информационных потоков, что в ряде случаев очень важно, т.к. в задачах, связанных с оперативным управлением, регулированием или контролем, существенную роль играет старение информации, поэтому задержки могут оказаться эквивалентными потере информации. Значительную сложность представляет выбор между избыточностью в информации и избыточностью в обслуживании. Информационная избыточность приводит к увеличению времени обслуживания каждого сообщения. Поэтому для компенсации потерь, связанных с отказом в обслуживании, вносится избыточность в обслуживании (увеличивают объем памяти буферных запоминающих устройств; число декодеров и т.д). Это усложняет аппаратуру и снижает надежность. Поэтому серьезной задачей является определение оптимальных соотношений по всем видам избыточности. Комплексный информационный подход к оценке потерь информации с учетом всех сторон функционирования технических средств позволяет добиться наивысшей эффективности работы системы связи.

5.1. Методы сокращения избыточности в системах передачи информации

5.1.1. Избыточность источника и эффективность ЭПП

Повышение эффективности СПИ неразрывно связано с сокращением избыточности. Это непосредственно следует из выражения  = 1—. При модуляции и кодировании в канале вносится избыточность с целью повышения помехоустойчивости. При кодировании источника избыточность сокращается с целью уменьшения (сжатия) необходимых данных для передачи сообщений. Более экономным может оказаться совместное кодирование для источника и для канала. Межсимвольная интерференция и межканальные помехи снижают эффективность реальных СПИ. Это снижение эффективности существенно зависит от частотной избыточности канала и избыточности системы разделения каналов. Следовательно, речь идет не просто о сокращении избыточности, а о рациональном ее использовании в различных звеньях (блоках) СПИ. Задача состоит в том, чтобы построить наиболее эффективную СПИ в целом при заданной степени сложности, а следовательно, и стоимости. Заметим, что информационная избыточность и аппаратурная избыточность определенным образом связаны между собой. Чем меньше информационная избыточность (больше ), тем сложнее система.

Рассмотрим -диаграммы (рис. 5.5) некоторых наиболее эффективных систем. Центральное место на этой диаграмме занимает система ФМ₄ без кодирования, и ее удобно принять за эталон для сравнения СПИ. Если начало отсчета перенести в точку ФМ₄, то в новой системе координат по вертикальной оси будет отсчитываться энергетический выигрыш  данной системы по сравнению с ФМ₄, а по горизонтальной оси — выигрыш  по удельной скорости передачи. В табл. 5.1 приведены значения этих выигрышей в дБ для некоторых систем, представленных на рис 5.4. Здесь же приведены значения информационной эффективности , рассчитанные по формуле для источника без избыточности (_и = 0).

Рис. 5.4. -диаграммы СПИ

На рис. 5.4 и в табл. 5.1 обозначено: ЦК — системы с циклическим кодированием (n = 511); СК — система со сверточным кодированием (v = 6 и R_K = ); БС₆ — система с биортогональными сигналами при М=16; ФМ₈-ЦК — система, в которой используется циклический код (п = 511) с многопозиционными сигналами ФМ₈; АФМ₁₆-СК — система, в которой используется сверточный код с кодовым ограничением v = 6 и многопозиционные сигналы АФМ₁₆.

Таблица 5.1

Выигрыш	ФМ4	ФМ16	АФМ16	БС16	ЦK (Rк=0.8)	СК (RK=0.5)	ФМ8=ЦК (п=255)	ЛФМ16=СК (RK=0.75)
, дБ , дБ 	0 0 0,47	-8,3 +3 0,51	-4,4 +3 0,65	+2,4 - 3 0,37	+3,1 -1 0,52	+5,4 -3 0,54	+ 1,4 +0,6 0,62	-0,3 +3 0,72

Из -диаграмм рис. 5.5 и табл. 5.1 видно, что при соответствующем выборе способов модуляции и кодирования информационная эффективная  достигает значения 0,5 и более.

Следовательно, возможности повышения эффективности СПИ за счет модуляции и помехоустойчивого кодирования в значительной мере исчерпаны (например, система АФМ₁₆-СК по информационной эффективности близка к идеальной системе). Дальнейшее повышение эффективности СПИ возможно за счет сокращения избыточности источника, которая для многих источников, как будет показано ниже, велика.

5.1.2. Информационные характеристики источника дискретных сообщений

Рассмотрим источник, который вырабатывает сообщения в виде последовательности дискретных элементов (букв), выбираемых из конечного множества (алфавита)

А = (а₁, а₂, ..., а_k) = {а_i}^K_i=1,

где К — объем алфавита источника.

Выбор букв происходит с некоторыми вероятностями, зависящими, как от предыдущих выборов, так и от конкретно рассматриваемого сообщения. Типичным примером такого сообщения является обычная телеграмма, представляющая собой последовательность букв (знаков), имеющих разную вероятность и статистически связанных между собой. При таком подходе в качестве математической модели источника принимается дискретный случайный процесс. Источник дискретных сообщений называется стационарным, если его вероятностное описание не зависит от начала отсчета времени.

Количество информации, вырабатываемое источником, определяется его энтропией. Если сообщения (буквы) статистически независимы (источник без памяти), то энтропия источника, равная среднему количеству информации на букву, определяется известным выражением

(5.1)

где P(a_i) —вероятность того, что на выходе источника появляется буква а_i.

Энтропия источника максимальна, когда все его сообщения имеют одинаковую вероятность Р(а) = 1 / К. В этом случае

(5.2)

Следовательно, величину энтропии Н(А) можно рассматривать как степень приближения распределения вероятностей сообщений данного источника к равномерному распределению.

Важным частным случаем является источник двоичных сообщений, для которого А = {а_i}²_i=1 = (0, 1). Если Р(0) =q, P(1)=1—q. 0  q  1, то согласно (5.1)

(5.3)

В общем случае сообщения, поступающие от источника, статистически зависимы. Примером может быть обычный текст, в котором появление той или иной буквы зависит от предыдущих букв. Так, после сочетания ЧТ вероятность появления гласных О, Е, И больше, чем согласных; после гласных не может появиться мягкий знак, мала вероятность появления в тексте более трех согласных подряд и т. д.

В ряде случаев последовательность сообщений на выходе источника образуют цепь Маркова. Стационарный источник, для которого каждая буква на выходе зависит лишь от l предыдущих букв, является марковским источником, состояниями которого являются все возможные последовательности из l букв. В частности, текст на русском языке достаточно хорошо аппроксимируется цепью Маркова.

Для стационарного источника зависимых дискретных сообщений энтропию можно определить как предел совместной энтропии H(A₁, А₂, ..., А_п) или условной энтропии

H(A_n/A₁, A₂, ..., А_п-1), т. е.

(5.4)

где

или

(5.5)

В теории информации доказывается, что энтропия источника зависимых сообщений всегда меньше энтропии источника независимых сообщений при том же объеме алфавита и тех же безусловных вероятностях сообщений.

Очевидно, имеют место следующие неравенства:

(5.6)

3десь Н₀ — максимальная энтропия (8.2); H₁ — энтропия источника независимых сообщений (8.1); Н₂ — энтропия источника, когда учитывается статистическая связь между двумя сообщениями (буквами); H₃ — энтропия источника с учетом трехбуквенных сочетаний и т. д.

Величина

(5.7)

называется избыточностью источника, а

(5.8)

определяет эффективность кодека источника. Для оценки эффективности устройств сжатия данных часто вводится величина , обратная величине _и:

(5.9)

которая называется коэффициентом сжатия.

Избыточность русского литературного языка близка к 80%. Избыточность поэтических произведений еще больше (энтропия меньше 1 бита на букву), так как в них имеются дополнительные вероятностные связи, обусловленные ритмом и рифмами. Деловые тексты, телеграммы весьма, однообразны, и поэтому их избыточность очень большая. Так, энтропия источника телеграфных сообщений не превышает 0,8 бит на букву (избыточность порядка 85%).

Избыточность дискретного источника  обусловлена тем, что элементы сообщения (буквы) не равновероятны (_р) и что между буквами имеется статистическая связь (обозначим эту избыточность через _). Очевидно, полная избыточность источника

(5.10)

Для русского языка _р=1 – H₁ / H₀= 0,13; _  0,73;  = 0,75. Следовательно, основная избыточность языка обусловлена статистической связью между буквами (_>>_p).

Для передачи по дискретному каналу сообщения источника представляют (кодируют) последовательностями кодовых (чаще всего двоичных) символов так, чтобы по этим последовательностям можно было однозначно (без ошибок) восстановить исходные сообщения при декодировании. Задача состоит в том, чтобы эффективно закодировать сообщения, т. е. обеспечить наиболее экономное представление букв источника бинарными последовательностями. При этом стремятся минимизировать среднее число битов на букву источника. Этот минимум, как известно, определяется энтропией источника H(A).

Теорема. При любом способе кодирования: 1) ; 2) существует способ кодирования, при котором величина будет сколь угодно близкой к H(A).

Таким образом, энтропия источника Н(А) определяет предельное значение двоичных символов, необходимых для представления букв источника. Теорема остается справедливой и в том случае, когда вместо двоичного используется m-ичное кодирование, но с той разницей, что логарифм при определении энтропии берется по основанию т. Для источника, все буквы которого независимы и равновероятны, оптимальным будет равномерный код. В этом случае H(A)=logK. Выберем для передачи каждой буквы последовательность из N бинарных символов. Количество различных последовательностей равно 2^N. Далее можно потребовать, чтобы 2^N = K (предполагается, что К — целая степень двух). Отсюда N = logK=H₀.

Таким образом, равномерный код, который широко используется в телеграфии (код Бодо), не является оптимальным для передачи текста телеграмм. При таком кодировании не учитывают статистические свойства источника и на передачу каждой из 32 букв русского языка тратится максимальное число двоичных символов, равное 5 бит. Согласно теореме 1 и статистике языка возможно более эффективное кодирование, при котором в среднем на букву русского текста будет затрачено не более 1,5 бит, т. е. примерно в 3 раза меньше, чем в коде Бодо.

Для реализации этих возможностей необходимо кодировать не отдельные буквы, а целые достаточно длинные последовательности букв (слова или даже фразы) и использовать для этого неравномерное кодирование, при котором более вероятным буквам (словам) присваивать короткие кодовые комбинации, а тем буквам (словам), которые встречаются редко, присваивать более длинные кодовые комбинации.

Задача эффективного кодирования наиболее актуальна не для передачи текста (телеграфии), а для других источников, обладающих большой избыточностью. К ним, в частности, относятся источники звуковых, видео- и телеметрических сообщений. В большинстве случаев эти источники относятся к классу источников непрерывных сообщений, которые рассматриваются далее.