- •2.1. Основные понятия…………………………………………….11
- •3.2. Кодирование в дискретных каналах…………………...……111
- •1. Информация. Сообщение. Сигнал
- •1.1. Основные понятия
- •1.2. Дискретизация непрерывных сообщений
- •2.1. Основные понятия
- •Из (2.19) следует, что
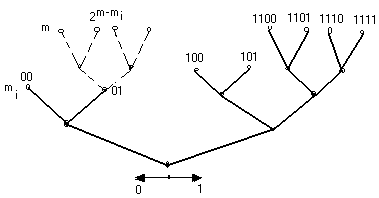
- •Р ис.2.4. Двоичное кодовое дерево для кода примера 2.19
- •Поскольку
- •Из свойства аддитивности тогда следует, что
- •Из условия (3.29) следует, что
- •3.2. Кодирование в дискретных каналах
- •Источник
- •5.1.3. Кодирование сообщений с заданной мерой верности
Из (2.19) следует, что
Рr (|X| ) 2X / 2 (2.20)
Это неравенство называется неравенством Чебышева.
Пусть X1, ..., Хn — независимые случайные величины, имеющие одинаковые распределения вероятностей р(х). Эти с. в. соответствуют n независимым экспериментам (например, n независимым бросаниям игральной кости), причем с. в. Хi соответствует эксперименту, проводимому в i-й момент времени. Пусть Y — среднее арифметическое указанных с. в., т. е.
![]() (2.21)
(2.21)
Легко определить математическое ожидание и дисперсию с. в. Y:
![]() (2.22)
(2.22)
где через mX обозначено математическое ожидание с. в. Х1,..., Хn (в силу одинаковой распределенности оно одинаково для всех случайных величин), и

Так
как с. в. Х1,...,
Хn
независимы, то при
![]() =0
при i
j
и
=2X,
где 2X
дисперсия
каждой из с. в. Хi.
Учитывая это, имеем
=0
при i
j
и
=2X,
где 2X
дисперсия
каждой из с. в. Хi.
Учитывая это, имеем
![]() (2.23)
(2.23)
Применим неравенство Чебышева к с. в. Y. В результате получим, что
![]()
Или
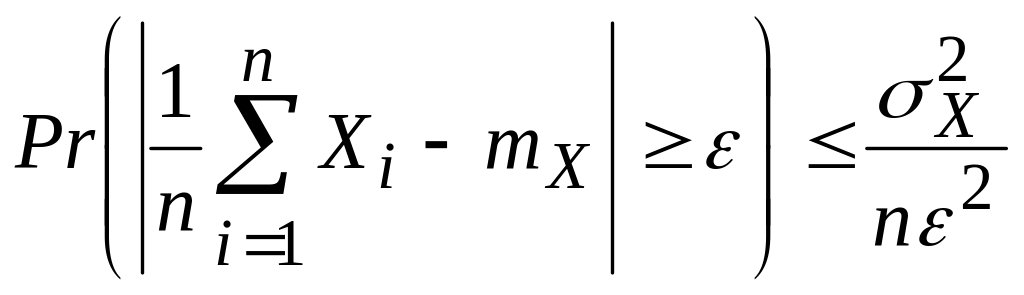 (2.24)
(2.24)
Полученный результат мы сформулируем в виде теоремы.
Т е о р е м а (Закон больших чисел в форме Чебышева.) Пусть Х1,..., Хn — независимые одинаково распределенные дискретные случайные величины, имеющие конечные математическое ожидание и дисперсию. Тогда для любых положительных и найдется такое N, зависящее от и , что для всех п > N вероятность того, что среднее арифметическое с. в. Х1,..., Хn будет отличаться от математического ожидания тХ каждой из случайных величин на величину, не меньшую чем , не превосходит :
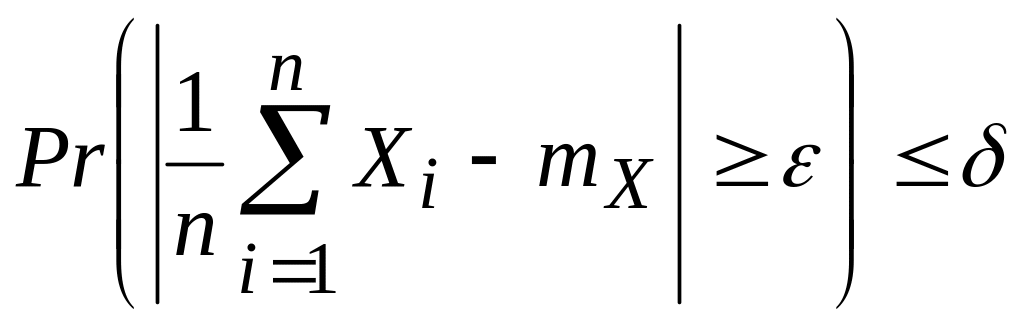 (2.25)
(2.25)
Пример 2.7. Пусть Х1,..., Хn — независимые одинаково распределенные случайные величины, принимающие значения 0 и 1 с вероятностями 1 — р и р соответственно. Легко видеть, что каждая из указанных с. в. имеет математическое ожидание, равное р, и дисперсию
![]()
С. в.
представляет собой относительное число (или долю) единиц в последовательности Х1,..., Хn. Применяя к с. в. Y закон больших чисел, получим, что при достаточно больших n для любого >0
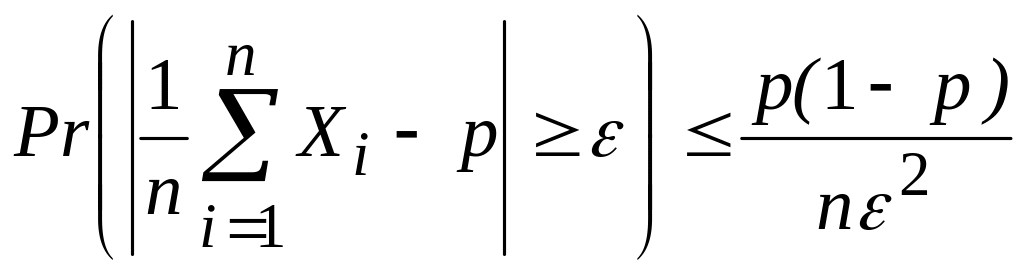 (2.26)
(2.26)
Другими сливами, доля единиц в достаточно длинной последовательности близки к вероятности появления единицы. Точный смысл этого утверждения проявляется с помощью неравенства (2.26). Конечно, не исключено, что в каком-либо эксперименте, в котором наблюдаются п случайных величин, определенных выше, доля единиц будет сильно отличаться от р. Однако вероятность этою события мала при достаточно больших п.
2.3. Количество информации в сообщении. Энтропия
В этом параграфе мы сформулируем основное теоретико-информационное понятие — количество информации в сообщении. Мы увидим, что информация определяется только вероятностными свойствами сообщений. Все другие их свойства, например, полезность для тех или других действий, принадлежность тому или иному автору и др., игнорируются. Это специфика теории информации, о которой иногда забывают, что часто приводит к неправильным выводам.
Пусть {Х, р (х)} ансамбль сообщений, X — {х1, ..., хL}.
Количеством собственной информации (или собственной информацией) в сообщении хiX называется число I (хi), определяемое соотношением
![]() ,
i=1, 2, . . ., L
(2.27)
,
i=1, 2, . . ., L
(2.27)
Основание, по которому берется логарифм в этом определении, влияет на единицу измерения количества информации. Наиболее часто употребляются логарифмы по основанию 2 и натуральные логарифмы. В первом случае единица измерения количества информации называется «бит», во втором — «нат».
Всюду ниже (если не оговорено противное) будем использовать только двоичные логарифмы и измерять количество информации в битах.
Рассмотрим основные свойства количества информации.
1. Собственная информация неотрицательна. Она равна нулю только в том случае, когда сообщение имеет вероятность 1. Такое сообщение можно рассматривать как неслучайное и известное заранее до проведения опыта. То сообщение имеет большую собственную информацию, которое имеет меньшую вероятность.
2. Рассмотрим ансамбль {XY, р (х, у)}. Для каждого сообщения из этого ансамбля, т. е. для каждой пары xi, yj, собственная информация I(xi, уj) = -log р (xi, уj). Если сообщения xi и уj статистически независимы, т. е. p(xi, уj)= p1 (хi) p2(yj), то
I(xi, уj) = —log p1(xi) - log p2 (уj) = I (xi)+I(yj) (2.28)
Это свойство называется свойством аддитивности информации Количество информации, определяемое соотношением (2.27), является действительной функцией на ансамбле {X, р (х)} и, следовательно, представляет собой случайную величину со значениями I(х1), ..., I(xL).
Математическое ожидание H (X) случайной величины I(х), определенной на ансамбле {X, р (х)}, называется энтропией этого ансамбля:
![]() (2.29)
(2.29)
Энтропия представляет собой среднее количество собственной информации в сообщениях ансамбля X.
Согласно определению собственная информация принимает бесконечные значения для сообщений, вероятности которых равны нулю. Однако энтропия любого дискретного ансамбля конечна, так как выражение вида zlogz при z=0 по непрерывности доопределяется как 0. Основанием для такого доопределения является следующее соотношение:
![]()
которое получается в результате применения правила Лопиталя для раскрытия неопределенности типа /.
Пример 2.8. Пусть X = {x1 , х2} — двоичный ансамбль и р (x1)=р, р (x2)=1-р — вероятности его сообщений. В этом случае энтропия является функцией одной переменной р
Н (X) =plog p(1 р) log (1 р) (2.30)
Эта функция показана на рис. 2.1. В точках р = 0 и р=1 она не определена и в соответствия с предыдущим замечанием доопределяется до нуля.
Поведение энтропии как функции от р может быть исследовано с помощью вычисления производной от правой части равенства (2.30).
Рассмотрим теперь свойства энтропии.
1. Энтропия всякого дискретного ансамбля неотрицательна:
H(Х)0 (2.31)
Равенство нулю возможно в том и только в том случае, когда существует некоторое сообщение хiX, для которого р (хi )= 1; при этом вероятности остальных сообщений равны нулю.
Неотрицательность следует из того, что собственная информация каждого сообщения дискретного ансамбля неотрицательна.
Равенство нулю возможно только тогда, когда каждое слагаемое в (2.29) равно нулю, а это равносильно условию, указанному выше.
2. Пусть L — число сообщений в ансамбле X, тогда
H(X) log (2.32)
причем равенство имеет место в том и только в том случае, когда все сообщения ансамбля имеют одинаковые вероятности.
Это неравенство можно доказывать с помощью стандартных методов поиска условного экстремума функции нескольких переменных. Однако имеется простое доказательство, основанное на следующем неравенстве для натурального логарифма:
ln x x 1 (2.33)
где равенство имеет место только при х = 1 (см. рис. 2.1). Неравенство (2.33) может быть проверено аналитически, если заметить, что разность In х — х + 1 имеет отрицательную вторую производную и стационарную точку при х=1.
Для доказательства (2.32) рассмотрим разность Н (X) — log L:
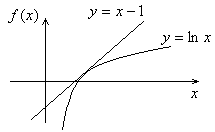
Рис.2.1. К неравенству для логарифма (2.33)

Теперь используем неравенство (2.33). В результате получим
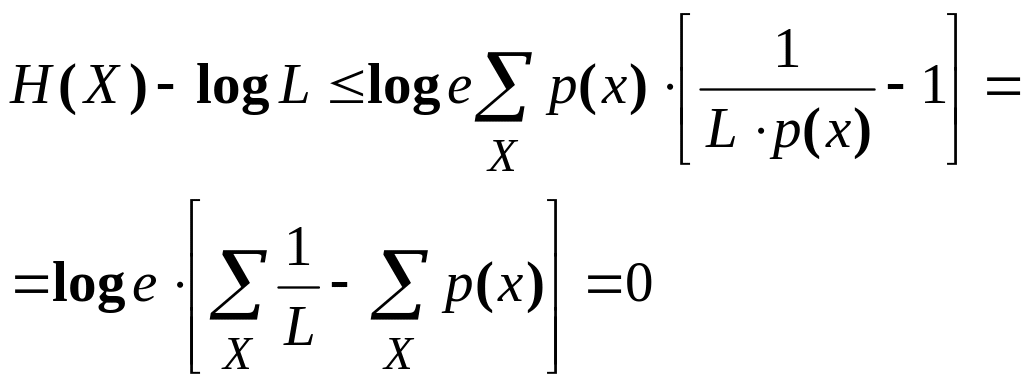
Отсюда следует неравенство (2.32). Поскольку
равенство в (2.33) имеет место только
тогда, когда аргумент логарифма равен
единице, то равенство в (2.32) имеет место
только тогда, когда![]() = 1 для всех х X,
т. е. когда р (х) = 1/L для
всех х X.
= 1 для всех х X,
т. е. когда р (х) = 1/L для
всех х X.
Таким образом, энтропия принимает наименьшее значение ансамбля, в котором сообщения предопределены заранее — одно из них появляется всегда, остальные — никогда. Энтропия принимает наибольшее значение log L, когда все сообщения одинаково вероятны. Эти два свойства часто используют для того, чтобы толковать энтропию как степень или меру неопределенности (степень неопределенности знаний экспериментатора) в эксперименте с получением сообщений ансамбля. Если сообщения заранее предопределены и экспериментатор знает, какое сообщение он получит, то неопределенность и энтропия равны нулю. Если ни одно сообщение не имеет преимуществ по отношению к другим и экспериментатор с одинаковыми шансами может получить любое сообщение, то как неопределенность, так и энтропия максимальны. Такое качественное толкование энтропии полезно, но не достаточно. Позже мы подробнее остановимся на содержательном смысле энтропии как скорости создания информации источником.
3. Пусть X и У — статистически независимые ансамбли. Тогда для каждой пары сообщений xiX и уjY выполняется равенство (2.28). Усредняя левую и правую части (2.28) по распределению р (xi, уj) и учитывая, что М[I (xi ,уj)] = Н (XY) есть энтропия ансамбля {XY, р (xi ,уj) }= p1 (xi) p2 (yj), получим
H(XY) = М [I(xi) + I(yj)] = H(Х) + H (Y) (2.34)
Это свойство называется свойством аддитивности энтропии.
2.4. Условная информация. Условная энтропия
Пусть {XY, р (х, у)} - пара совместно заданных дискретных ансамблей {X, p (х)} и {Y, р (у)}. Как указывалось выше, на каждом из множеств X и Y могут быть определены различные условные распределения. Зафиксируем некоторое сообщение yY, р (у)0, и рассмотрим условное распределение р (х|у) на X. Для каждого сообщения хX в ансамбле {X, р(х|у)} определена собственная информация
![]() (2.35)
(2.35)
которая называется условной собственной информацией сообщения х при фиксированном сообщении у. Как и раньше, I (х|у) можно рассматривать как случайную величину на ансамбле {Х; р (х у)}; ее математическое ожидание
![]() (2.36)
(2.36)
называется условной энтропией ансамбля X относительно сообщения уY.
Условную энтропию Н (Х|у) можно рассматривать как с. в. на ансамбле {Y, p (у)}.
Математическое ожидание Н (X|Y) случайной величины Н (Х|у), определенной на ансамбле {Y,p(y)}, называется условной энтропией ансамбля X относительно ансамбля Y:
 (2.37)
(2.37)
Следует помнить, что условная вероятность р(х|у), а следовательно, условная собственная информация I(х|у) и условная энтропия Н(Х|у), определены только для тех сообщений уY, вероятности которых отличны от нуля. Поэтому всюду ниже мы будем считать, что указанное условие выполнено и соответствующие вероятности не равны нулю. Если в ансамбле некоторые сообщения имеют нулевые вероятности, то мы будем исключать эти сообщения из рассмотрения, переходя тем самым к ансамблю, все сообщения которого имеют ненулевые вероятности.
Мы ввели условную энтропию Н (Х|Y), рассматривая вначале условную энтропию H(Х|y) при фиксированном сообщении как случайную величину на ансамбле Y, а затем находя математическое ожидание этой с. в. Можно поступить иначе и рассмотреть условную собственную информацию I(х|у) как действительную функцию, заданную на ансамбле {XY, р (х, у)} и, следовательно, как с. в. на этом ансамбле. Тогда энтропия H (Х|Y) есть математическое ожидание с. в. I(х|у) и может быть непосредственно определена с помощью правой части формулы (2.37).
Теперь мы продолжим рассмотрение свойств энтропии и условной энтропии.
1. Условная энтропия не превосходит безусловной энтропии того же ансамбля:
H(X|Y)H(Х) (2.38)
причем равенство имеет место в том и только том случае, когда ансамбли X и Yстатистически независимы.
Доказательство этого неравенства проводится с помощью неравенства для логарифма (2.33):
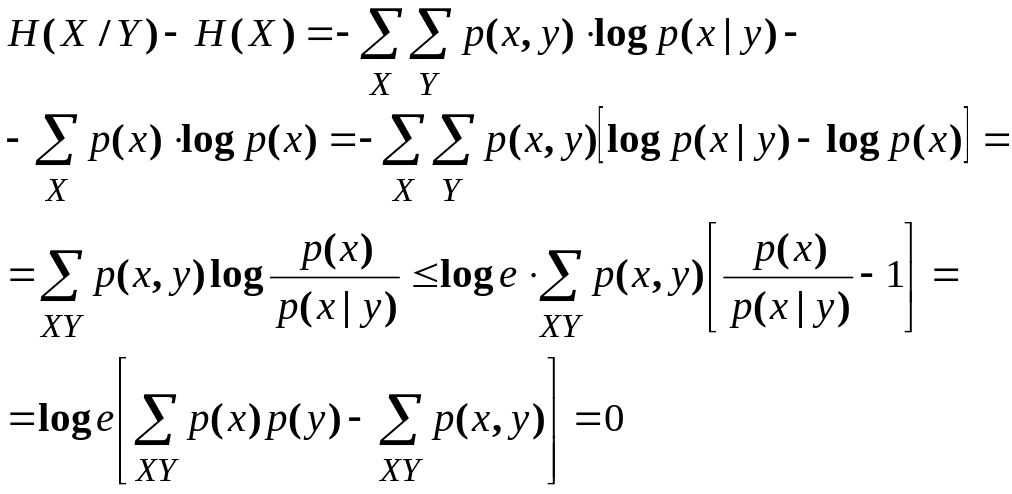 (2.39)
(2.39)
Равенство выполняется в том и только в том случае, когда р (х|у)=р (х) для всех х X, уY.
2. Математическое ожидание Н (XY) собственной информации пары сообщений (х, у)
![]() (2.40)
(2.40)
по определению представляет собой энтропию ансамбля XY. Используя соотношение р (х, у) = р (у)р(х|у) (определение условной вероятности), можно получить, что
 (2.41)
(2.41)
Аналогично, используя соотношение р (х, у) = р (х) р (у|х), можно получить, что
H(ХY) = H(Х)+H(Y|Х) (2.42)
Эти свойства также называются свойствами аддитивности энтропии. В случае независимых ансамблей соотношения (2.41) и (2.42) переходят в (2.34).
3. Предположим, что задан ансамбль {X,
р (х)} и на этом ансамбле определено
отображение (X)
множества X в множество
Y. Это отображение определяет
ансамбль {Y, р (у)}, для
которого p(y)=![]() .
Пусть H(Х), H
(Y) — энтропии ансамблей
X и Y
соответственно. Тогда
.
Пусть H(Х), H
(Y) — энтропии ансамблей
X и Y
соответственно. Тогда
H(Y)H(Х) (2.43)
и знак равенства имеет место в том и только том случае, когда отображение (х) обратимо, т. е. когда каждому элементу уY соответствует один и только один элемент хX.
Для доказательства неравенства (2.43) заметим, что совместное распределение вероятностей р (х, y) на произведении множеств X и Y задается следующим образом: р (х, у)= р (у|х) р (х), где р (у|х) = 1 для у =(х) и р (у|х)=0 для остальных уY. Другими словами, каждое сообщение ансамбля X однозначно определяет сообщение ансамбля Y (в этом случае говорят, что ансамбль X однозначно определяет ансамбль Y). Тогда, как легко показать, H(У|X)=0. Из аддитивности и неотрицательности энтропии получим, что
H (Y) H (Y)+H (X | Y)= H (X)+ H (Y | X)= H (X) (2.44)
Таким образом, при произвольных отображениях, задаваемых функцией (х), хX, при которых ансамбль X переходит в некоторый другой ансамбль Y, энтропия не возрастает. Энтропия не изменяется тогда и только тогда, когда H (X | Y) = 0, т. е. когда ансамбль Y однозначно определяет ансамбль X. Другими словами, энтропия сохраняется только при обратимых преобразованиях.
4. Пусть {XYZ, р (х, у, z)} —три совместно заданных ансамбля XYZ и
I(x | y, z)= log р (x | y, z) (2.45)
условная собственная информация сообщения х при фиксированной паре сообщений у, z, где
 (2.46)
(2.46)
Число
H(X|YZ)=M[
I(x | y,
z) ]=
![]() (2.47)
(2.47)
называется условной энтропией ансамбля X относительно пары ансамблей YZ.
Имеет место следующее неравенство:
Н (X | YZ) H (X | Y) (2.48)
которое доказывается таким же методом, как и неравенство (2.38). Равенство в (2.48) выполняется в том и только том случае, когда р (х | у, z) = р(х | у) для всех (х, у, z)XYZ, т. е. когда при данном сообщении у ансамбли X и Z статистически независимы.
Это неравенство легко обобщается на случай п совместно заданных ансамблей. Рассмотрим ансамбль {Х1 ... Хn, р(х(1), ..., х(n))}. Тогда для любых s и т, 1 s m i, имеет место следующее неравенство:
H (Хi | Xi-1… Xi-s) . H (Хi | Xi-1…Xi-m) (2.49)
Его левая и правая части определены, как и в (2.48), а именно, как математические ожидания соответствующих информации.
Для вывода еще одного важного неравенства заметим, что для любой последовательности (х(1), ..., х(п)) Х1 ... Хп ее вероятность может быть записана следующим образом:
![]() (2.50)
(2.50)
Где
![]() (2.51)
(2.51)
И
![]() (2.52)
(2.52)
Тогда
![]() (2.53)
(2.53)
Где
![]() (2.54)
(2.54)
— условная собственная информация сообщения x(i). Усредняя обе части соотношения (2.53), получим
![]()
![]() (2.55)
(2.55)
Используя (2.49), можно записать
![]() (2.56)
(2.56)
2.5. Энтропия на сообщение дискретного стационарного источника
Рассмотрим дискретный стационарный источник, выбирающий сообщения из множества X. Для удобства мы будем обозначать через Xi ансамбль сообщений в i-й момент времени, хотя множества {Xi} в каждый момент времени совпадают между собой и совпадают с множеством X. Для стационарных источников n-мерные распределения вероятностей п = 1, 2, ... не зависят от сдвига по оси времени. Следовательно, любые величины, зависящие только от n-мерных распределений вероятностей, одинаковы для всех сдвигов по оси времени. В частности, энтропия H(Xп), где Хп = Xi+1 ... Xi+n, не зависит от выбора числа i, указывающего расположение п последовательных моментов времени на оси времени. Поэтому всюду при рассмотрении стационарных источников мы будем опускать этот индекс i из обозначения энтропии.
Пусть X n-1 и Х n = Х n-1 Хn — два ансамбля последовательностей длины п — 1 и п соответственно и
![]() (2.57)
(2.57)
условная энтропия ансамбля Хп относительно ансамбля Xn-1.
Т е о р е м а Для всякого дискретного стационарного источника последовательность Н (Хn | Xn-1), п — 1, 2, ..., имеет предел:
![]() (2.58)
(2.58)
Покажем вначале, что последовательность
H(Х1), H(Х2|Х1), . . ., Н(Хn |Xn-1 Х1 ), . . . (2.59)
не возрастает. Хотя эта последовательность есть последовательность энтропии с возрастающим числом условий, непосредственно применить неравенство (2.49) нельзя, так как (2.59) есть последовательность энтропии различных ансамблей, а не одного ансамбля, как в (2.49). Однако в случае стационарных источников для всех целых i, j, п
Н(Хj |Xj-1 Хj-i )= Н(Хn |Xn-1 Хn-i ) (2.60)
поскольку левая и правая части этого равенства определяются только i + 1 -мерными распределениями вероятностей. Применяя теперь неравенство (2.49), получим, что последовательность (2.59) не возрастает.
С другой стороны, все члены этой последовательности ограничены снизу нулем. Любая невозрастающая последовательность, ограниченная снизу, имеет предел. Обозначая этот предел через H(X | X), получим утверждение теоремы.
Рассмотрим теперь последовательность
Нn (X)![]() n= 1, 2, . . . (2.61)
n= 1, 2, . . . (2.61)
Если эта последовательность имеет предел при п , то этот предел представляет собой среднее количество информации, порождаемое источником в единицу времени, и называется энтропией стационарного источника на сообщение.
Т е о р е м а . Для, всякого дискретного стационарного источника последовательность (2.61) имеет предел, причем
![]() (2.62)
(2.62)
Покажем вначале, что последовательность Hп (Х), п = 1, 2, ..., не возрастает. Рассмотрим энтропию H(Хп+1), где Xn+1=ХпXп+1 — ансамбль последовательностей сообщений длины п + 1. Используя свойство аддитивности энтропии, можно записать
H(Хп+1)=H(Хп)+H(Хп+1| Хп)=H(Хп) +H(Хп|Хп)
H(Хп)+H(Хп|Хп-1) (2.63)
где второе равенство есть следствие стационарности (см. 2.61)), а неравенство — следствие неравенства (2 .49). Используя (2 .56) и (2.49), можно получить
![]() (2.64)
(2.64)
Неравенства (2.63) и (2.64) совместно дают
![]()
Деля обе части этого неравенства на п + 1, получим
Hп+1 (X)Hп(X) (2.65)
т. е. рассматриваемая последовательность энтропии не возрастает.
Поскольку последовательность (2.61) не возрастает и каждый ее член ограничен снизу нулем, то она имеет предел. Покажем теперь, что этот предел совпадает с H (X | X).
Можно записать
 (2.66)
(2.66)
где k п. Выберем k таким, чтобы для заданного положительного выполнялось неравенство
H(Хk+1|
Хk)-H
(Х| Х)![]() (2.67)
(2.67)
Это всегда можно сделать, так как последовательность H(Xk+1|Xk), k = 0, 1, ..., имеет предел H (Х| X) и стремится к нему, не возрастая. По выбранному k определим N так, чтобы для всех п>N
![]() (2.68)
(2.68)
Тогда получим, что для любого >0 всегда найдется такое N, что для всех п > N
Нп(Х)Н(Х|Х) + (2.69)
С другой стороны,
![]() (2.70)
(2.70)
Так как — произвольное положительное число, то из (2.69) и (2.70) следует, что Н (X | X) является пределом последовательности Нп(Х), n = 1, 2, ... Теорема доказана.
2.6. Постановка задачи кодирования дискретных источников равномерными кодами
Обозначим через A некоторое множество, состоящее из D, D>1, элементов: А = {a1 ,…, aD}. Назовем его алфавитом кода источника. Элементы множества А будем называть кодовыми символами.
Последовательность кодовых символов называется кодовым словом, а любое семейство кодовых слов — кодом над алфавитом А.
Пример 2.9. Пусть А — множество букв русского алфавита (включая пробел) Любая последовательность букв заданной длины п является кодовым словом длины n над алфавитом A. Так, АБЬЮЙ-АБ есть слово длины 8 (-пробел). Другим примером кодового алфавита является множество десятичных цифр, включая пробел. Следующие последовательности -0001, -099 являются примерами двух кодовых слов длины 5 и 4 соответственно.
Пример 2.10. Пусть А = {0, 1}—двоичный алфавит. Множество последовательностей {011, 1100, 11,1} является кодом объема 4 над двоичным алфавитом. Это пример кода, слова которого имеют разную длину. Множество последовательностей {00, 01, 10, 11} также является двоичным кодом объема 4.
Код называется равномерным, если все его слова имеют одинаковую длину m, это число называется длиной кода. Если хотя бы два кодовых слова имеют различные длины, то код называют неравномерным.
Количество различных слов равномерного кода длины т не превосходит Dm — числа различных D-ичных последовательностей длины m. Количество различных слов неравномерного кода с максимальной длиной кодовых слов т не превышает D(Dт—1)/(D—1).
Кодированием сообщений ансамбля X посредством кода называется отображение (необязательно взаимно однозначное) множества сообщений в множество кодовых слов.
Пример 2.11. Пусть X— {x1 ..., х6}. Возможны следующие способы кодирования посредством двоичных кодов:
a) x1 000; x2 001; х3 010; x4 011; х5 100; х6 101;
б) x1 00; x2 01; х3 00; x4 10; х5 01; х6 11;
в) x1 00; x2 00; х3 01; x4 01; х5 10; х6 11.
В п. a) кодирование однозначно. В пп. б) и в) приведены два различных способа кодирования с одним и тем же множеством кодовых слов.
Рассмотрим теперь кодирование дискретного источника. Для того чтобы лучше понять основные проблемы, возникающие при кодировании, мы рассмотрим несколько подробных примеров.
Пример 2.12. Предположим, что на центральном телеграфе введена автоматическая обработка телеграмм, записанных в алфавите, объем которого для простоты будем считать равным 64 буквам (сюда входят сами буквы, русские и латинские, цифры, знак пробела и некоторые вспомогательные знаки). Предположим, что эффективность такой обработки определяется количеством телеграмм, которые можно ввести в запоминающее устройство (ЗУ) обрабатывающего устройства. Пусть объем ЗУ равен N двоичным ячейкам. Чтобы осуществить запись телеграмм в ЗУ, необходимо закодировать телеграммы с помощью двоичного кода.
Рассмотрим вначале так называемое побуквенное кодирование. В этом случае используют код, содержащий 26 = 64 кодовых слова, и каждой букве телеграммы сопоставляют некоторое кодовое слово. Предположим, что используется равномерный код, в котором все слова имеют длину 6 двоичных символов. При этом в ЗУ можно записать N/6 букв. Если считать, что средняя длина телеграммы — 20 слов, а средняя длина слова 8 букв, то в ЗУ можно поместить примерно N/960 телеграмм.
Второй способ кодирования состоит в том, что выделяется специальный словарь, например, из 213 = 8192 слов (такого словаря достаточно для составления практически любой телеграммы). Каждое слово словаря может быть закодировано с помощью двоичной последовательности длиной 13 символов. В этом случае в ЗУ можно записать N/260 телеграмм, т. е. в три-четыре раза больше, чем в первом случае.
При кодировании можно условиться о том, что всякое слово, не содержащееся в словаре, кодируется так же, как слово «ошибка». При декодировании вместо этих слов будет воспроизводиться слово «ошибка».
Таким образом, второй способ является значительно более эффективным. Полученный эффект объясняется тем, что далеко не всякая последовательность букв встречается в языке, а тем более среди слов телеграмм. Имеются почти невероятные буквосочетания, например, АБЬЮЙ-АБ. Однако необходимо помнить о том, что вероятность такого буквосочетания хотя и мала, но не равна нулю. Последнее следует, например, из того, что оно появляется в настоящем тексте. Поэтому при кодировании возможны ошибки.
Заметим, что при побуквенном кодировании все слова телеграмм могут быть однозначно (безошибочно) закодированы.
Изложенная в примере 2.12 идея может быть применена для кодирования произвольных дискретных источников равномерными кодами.
Предположим, что множество всех последовательностей длиной п из сообщений источника разбито на два подмножества. Первое из них образовано всеми теми последовательностями (блоками длиной п), которые сопоставлены с кодовыми словами взаимно однозначно. Это подмножество называется множеством однозначно кодируемых и декодируемых блоков. Второе подмножество образовано всеми остальными блоками, каждому из которых сопоставляется одно и то же кодовое слово (Можно сопоставлять и различные кодовые слова. Это не существенно. Существенно лишь, что эти кодовые слова использованы для представления однозначно кодируемых и декодируемых блоков.). Последнее подмножество называется множеством неоднозначно кодируемых и декодируемых блоков. Все кодовые слова имеют одинаковую длину т, которая определяется числом М кодовых слов: m — наименьшее целое, удовлетворяющее неравенству Dm M, где D — объем кодового алфавита. При кодировании последовательность сообщений на выходе источника разбивается на блоки длиной п, каждому блоку кодер сопоставляет соответствующее кодовое слово.
Описанный метод кодирования дискретного источника мы будем называть равномерным кодированием. Ошибкой равномерного кодирования является событие, состоящее в появлении неоднозначного кодируемого блока.
При равномерном кодировании количество
D-ичных кодовых символов,
приходящихся на одно сообщение, равно
![]() .
.
Число
![]() (2.71)
(2.71)
называется скоростью равномерного кодирования источника посредством кода с М кодовыми словами при разбиении последовательности сообщений на блоки длины п. Скорость равномерного кодирования измеряется в двоичных символах на сообщение.
Количество двоичных символов на сообщение
естественно измерятьчислом
![]() log М, а не
log М, а не
![]() .
Очевидно, что эти два числа совпадают,
когда число кодовых слов равно неравенству
Dm. В
остальных случаях именно первое из этих
чисел равно количеству двоичных символов
на сообщение.
.
Очевидно, что эти два числа совпадают,
когда число кодовых слов равно неравенству
Dm. В
остальных случаях именно первое из этих
чисел равно количеству двоичных символов
на сообщение.
Как видно из примера 2.12, существенной частью задания равномерного кода является указание множества последовательностей сообщений источника, которые кодируются с помощью кодовых слов однозначно. Все коды, которые имеют одинаковое число кодовых слов и однозначно кодируют одно и то же множество сообщений, имеют одинаковую скорость и одинаковую вероятность ошибки. Поэтому ни сами кодовые слова, ни способ сопоставления кодовых слов и однозначно кодируемых сообщений не имеют значения с точки зрения качества кода.
При кодировании с помощью равномерных кодов основная задача состоит в определении наименьшей возможной скорости кодирования, при которой вероятность ошибки может быть сделана произвольно малой. Наименьшая достижимая скорость кодирования является характеристикой источника сообщений и называется скоростью создания информации.
Скоростью создания информации дискретным источником при равномерном кодировании называется наименьшее число H такое, что для любого R > H и любого сколь угодно малого положительного числа найдется п (длина кодируемых сообщений) и равномерный код со скоростью кодирования R, для которого вероятность неправильного декодирования не превосходит .
В следующем примере показано, что по крайней мере для некоторых источников можно построить код с заданной малой вероятностью ошибки декодирования.
Пример 2.13. Рассмотрим двоичный источник без памяти, независимо выбирающий сообщения из множества X = {О, 1}, причем единица выбирается с вероятностью р < 1/2. Этот источник возможно кодировать побуквенно. При этом на каждое сообщение будет затрачиваться 1 двоичный символ. При любом безошибочном кодировании с помощью равномерного кода скорость кодирования не будет меньше единицы.
Предположим, что допускается некоторая достаточно малая вероятностьошибки при кодировании. Рассмотрим множество Хп всех последовательностей длины п на выходе источника. Оно содержит 2п последовательностей. Пусть >0 и Тп — это подмножество множества Хп, состоящее из всех последовательностей, в которых число единиц k удовлетворяет условию
| k n p | n (2.72)
Согласно закону больших чисел вероятность
появления на выходе источника
последовательности, принадлежащей
множеству Тп , не меньше, чем 1 —![]() и может быть сделана как угодно близкой
к единице выбором достаточно большого
п.
и может быть сделана как угодно близкой
к единице выбором достаточно большого
п.
Рассмотрим кодирование, при котором имеется равномерный код, состоящий из Мп кодовых слов, где Мп — количество различных последовательностей в Тп и каждой последовательности из Тп сопоставляется свое кодовое слово. Всем же последовательностям, не принадлежащим Тп, ставится в соответствие одно и то же слово, например, первое. При таком кодировании все последовательности сообщений из Тп будут воспроизводиться правильно, а при появлении на выходе источника последовательности, не принадлежащей Тп, будет происходить ошибка. Очевидно, что вероятность ошибки может быть сделана как угодно малой выбором достаточно большого п.
Оценим теперь скорость кодирования. Для этого необходимо оценить число Мп:
![]() (2.73)
(2.73)
где 2п + 1 — количество слагаемых в сумме, a k0 соответствует максимальному слагаемому. При р + 1/2 максимальное слагаемое получается при k0 = [п (р +)], где [x] — целая часть х. Используя верхнюю границу для числа сочетаний, получим, что
Мn(2n + 1) (2n0(10))1/2 2nh (o), (2.74)
где 0 =k0/n и h(0)=— 0 log0 —(1—0 )log(1—0 ). При этом скорость кодирования
![]() (2.75)
(2.75)
стремится к h (р + ) при больших п.
Возьмем, например, р = 0,1. Если положить R = 0,66 и найти из уравнения h(0,1+) = 0,66, то получим = 0,074. Вероятность ошибки Ре при кодировании последовательности сообщений длины п, т. е. вероятность появления такой последовательности, количество единиц в которой удовлетворяет неравенству | k — пр | > n, можно оценить, правда весьма грубо, с помощью неравенства Чебышева
![]()
откуда получается Ре 17/n . Использование Ре для оценки асимптотической формулы Муавра — Лапласа дает при больших п
![]()
![]() =
—0,03n.
=
—0,03n.
Выбирая достаточно малым, можно приближать скорость кодирования как угодно близко к величине h (р) = 0,47 — энтропии двоичного ансамбля, для которого одно из сообщений имеет вероятность р= 0,1.
Ниже мы покажем, что энтропия определяет наименьшее возможное значение скорости кодирования и согласно определению 2.6.4 дает величину скорости создания информации при равномерном кодировании.
Для того чтобы установить, что некоторая величина, скажем H, является скоростью создания информации, необходимо доказать два утверждения:
1. Для любого R > Н и произвольного положительного найдутся п и код со скоростью R, кодирующий отрезки сообщений длины п, для которого вероятность ошибки не больше . Такое утверждение называется прямой теоремой кодирования.
2. Для любого R < Н найдется зависящее от R положительное число такое, что для всех п и для всех равномерных кодов со скоростью R вероятность ошибки при декодировании больше, чем это . Другими словами, вероятность ошибки не может быть сделана равной нулю или сколь угодно малой. Это утверждение называется обратной теоремой кодирования.
2.7. Теорема о высоковероятных множествах дискретного источника без памяти
Рассмотрим дискретный источник без памяти, выбирающий сообщения из конечного множества X. Согласно определению источника без памяти вероятность каждой последовательности сообщении x(x(1),…,x(n) )Xп на его выходе может быть записана в виде
![]() (2.76)
(2.76)
где р (х), х X, — распределение вероятностей на множестве X. Будем полагать, что р (х) >0 для всех х X. В противном случае всегда можноперейти к рассмотрению суженного множества, для которого это предположение верно.
Пусть Н (X) — энтропия ансамбля {X, р (х)} и — некоторое положительное число. Определим подмножество Тп () множества Хп следующим образом:
![]() (2.77)
(2.77)
где I (x) = —log р (х) — собственная информация последовательности xХп.
Т е о р е м а Для любых положительных чисел и найдется N такое, что для всех п > N выполняются следующие неравенства:
![]() (2.78)
(2.78)
![]() (2.79)
(2.79)
где | Тп () | — число элементов в множестве Тп ().
В силу отсутствия памяти у источника
![]() (2.80)
(2.80)
где I(x(i)), i = 1, 2, ..., п, — независимые одинаково распределенные случайные величины, принимающие ограниченные значения. К последовательности таких случайных величин можно применить закон больших чисел, из которого следует, что при любых >0 и >0 найдется N такое, что при всех п > N
 (2.81)
(2.81)
или
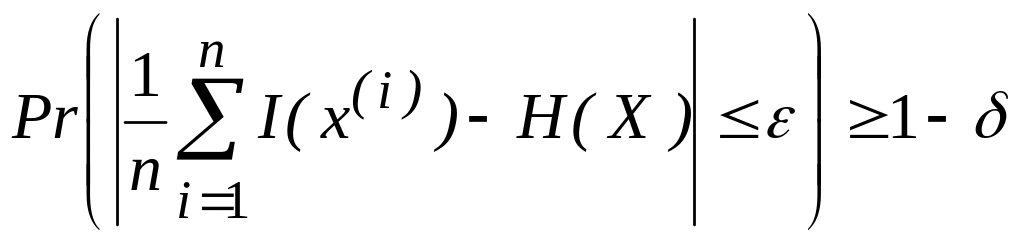 (2.82)
(2.82)
Нетрудно увидеть, что вероятность Рr (хТп()) равна левой части неравенства (2.82) и, следовательно, неравенство (2.78) справедливо.
С другой стороны, из определения множества Тп () следует, что для всякой последовательности хТп ()
![]() (2.83)
(2.83)
Суммируя обе части левого неравенства по всем элементам Тп(), получим следующую цепочку неравенств:
![]() (2.84)
(2.84)
откуда следует правое неравенство в (2.84). Суммируя теперь обе части правого неравенства в (2.83) по всем элементам Тп (), получим, что для достаточно больших п
![]() (2.85)
(2.85)
что дает левое неравенство в (2.79). Теорема доказана.
Теорема показывает, что последовательности
сообщений на выходе дискретного источника
без памяти могут быть подразделены на
две группы: Тп()
и
![]() (),
где второе множество — это дополнение
первого до Хп. Последовательности
из первой группы обладают тем свойством,
что их вероятности достаточно близки
друг к другу (см. (2.83)) и суммарная
вероятность всех элементов этого
множества весьма близка к единице (см.
(2.78)). Тем не менее, множество Тп
()
может составлять лишь очень малую долю
по числу элементов от множества Хп.
Действительно, если обозначить число
элементов в X через L,
то | Хп |= Ln
= 2nlogL
. Доля множества
Тп ()
в Хп
(),
где второе множество — это дополнение
первого до Хп. Последовательности
из первой группы обладают тем свойством,
что их вероятности достаточно близки
друг к другу (см. (2.83)) и суммарная
вероятность всех элементов этого
множества весьма близка к единице (см.
(2.78)). Тем не менее, множество Тп
()
может составлять лишь очень малую долю
по числу элементов от множества Хп.
Действительно, если обозначить число
элементов в X через L,
то | Хп |= Ln
= 2nlogL
. Доля множества
Тп ()
в Хп
![]() (2.86)
(2.86)
Если log L — Н (X) — = >0, т. е. если энтропия источника строго меньше, чем log L, и достаточно мало, то а убывает к нулю при увеличении п как 2 -n.
Эти свойства множества Тп() позволяют называть его множеством типичных последовательностей или высоковероятным множеством дискретного источника без памяти.
Следующие примеры показывают структуру высоковероятных множеств для двух двоичных источников.
Пример 2.14. Рассмотрим двоичный источник сообщений о результатах подбрасывания симметричной монеты. Вероятности сообщений одинаковы и равны 1/2. Энтропия такого ансамбля Н(X)=1. Вероятность любой последовательности сообщений длины п не зависит от последовательности и равна 2-n. Отсюда следует, что I(х) = п = пН(X), т. е. все последовательности из Хп принадлежат множеству Тп () при любом . Другими словами, для этого источника Хп = Тп () и высоковероятное множество совпадает с множеством всех последовательностей.
Пример 2.15. Пусть двоичный источник без памяти выбирает сообщения из множества Х= {О, 1}, причем 1 появляется с вероятностью р < 1/2. Для такого источника
Н (X)= —р log р — (1 — р)log (1 — р),
р(х)=рt(1-p) n-t , xXn (2.87)
где t— количество единиц
в последовательности х. Обозначая
![]() ,
получим
,
получим
![]() (2.88)
(2.88)
и, следовательно,
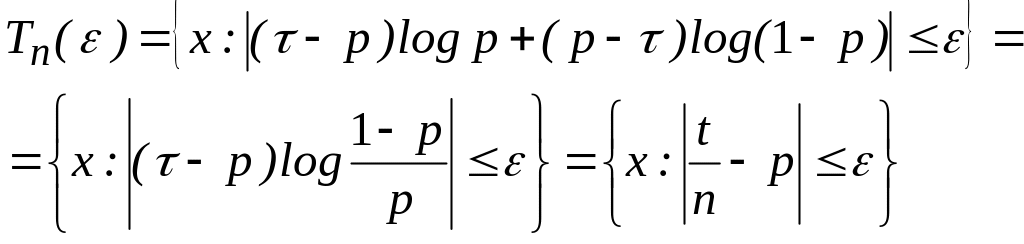 (2.89)
(2.89)
где
![]() .
.
Таким образом, высоковероятное множество для рассматриваемого источника состоит из таких последовательностей х Хп, число единиц в которых близко к пр. Например, если р = 0,1, то Н(X) = 0,47. Высоковероятное множество состоит из последовательностей, число единиц в которых близко к 0,1n. Количество последовательностей в этом множестве близко к 2nН(Х) =2n0,47 . Так, при п = 100 это число примерно равно 10 -16.
2.8. Скорость создания информации дискретным источником без памяти при равномерном кодировании
В этом параграфе мы покажем, что скорость создания информации дискретным источником без памяти при равномерном кодировании равна его энтропии. Как отмечалось в 2.6, для доказательства этого утверждения нужно доказать прямую и обратную теоремы кодирования. Каждый код, кодирующий сообщения источника, характеризуется скоростью кодирования — отношением логарифма числа кодовых слов к длине кодируемых сообщений, множеством однозначно кодируемых сообщений и вероятностью ошибки. Поэтому, говоря о том, что существует код со скоростью R, кодирующий источник с вероятностью ошибки Ре, мы подразумеваем, что существуют п, код с 2nR кодовыми словами и множество однозначно кодируемых последовательностей сообщений Тп Хn, для которых вероятность ошибки равна Рe.
Предположим, что дискретный источник без памяти выбирает сообщения из множества X с распределением вероятностей р(х), р(x) 0 для всех хX, и H (X) — энтропия ансамбля {Х, p(х)}.
Т е о р е м а (прямая теорема). Пусть R > H(X), тогда для любого положительного существует код со скоростью R, который кодирует дискретный источник без памяти с вероятностью ошибки, не превышающей .
Согласно теореме 2.7.1 для любых положительных и найдется N такое, что для любого п>N вероятность появления на выходе источника последовательности сообщений х, не принадлежащей высоковероятному множеству Тп(), не превосходит . Если выбрать Тп() в качестве множества однозначно кодируемых последовательностей, то вероятность ошибки декодирования не будет превышать . При этом количество кодовых слов не должно быть меньше числа элементов в множестве Тп(). Это условие будет удовлетворено, если
2nR 2n[H(X)+] (2.90)
откуда следует, что R H(X) + . Теорема доказана.
В теореме утверждается существование кода, кодирующего дискретный источник без памяти с произвольно малой вероятностью ошибки. В действительности доказано нечто большее, а именно, что для любых , > 0 найдется N и последовательность кодов, кодирующих отрезки сообщений длины п, п = N+1, N + 2, ..., и имеющих скорость R = H(X) + , причем для каждого кода этой последовательности вероятность ошибки не превосходит .
Т е о р е м а (обратная теорема). Пусть R<H(X), тогда существует, зависящее от R положительное число такое, что для каждого кода, кодирующего дискретный источник без памяти со скоростью R, вероятность ошибки Ре не меньше, чем .
Кроме того, для любой последовательности кодов со скоростью R
![]() (2.91)
(2.91)
где Реп — вероятность ошибки для кода, кодирующего отрезки сообщений длины п.
Докажем сначала справедливость соотношения (2.91). Пусть = H(X) — R > 0 и Тп (/2), п=I, 2, ..., — последовательность высоковероятных множеств. Обозначим через Тп, п = 1, 2, ..., последовательность произвольных множеств таких, что ТпXn и
|Тп| = 2nR= 2n[H(X) ] (2.92)
Для каждого п множество Тп будем рассматривать как множество однозначно кодируемых последовательностей сообщений. Поэтому (см. рис. 2.2)
![]() (2.93)
(2.93)
где Тп (/2) — дополнение множества Тп (/2) до Хп и — символ пересечения множеств. Из теоремы о высоковероятных множествах следует, что
![]() = 0, > 0.
(2.94)
= 0, > 0.
(2.94)
Р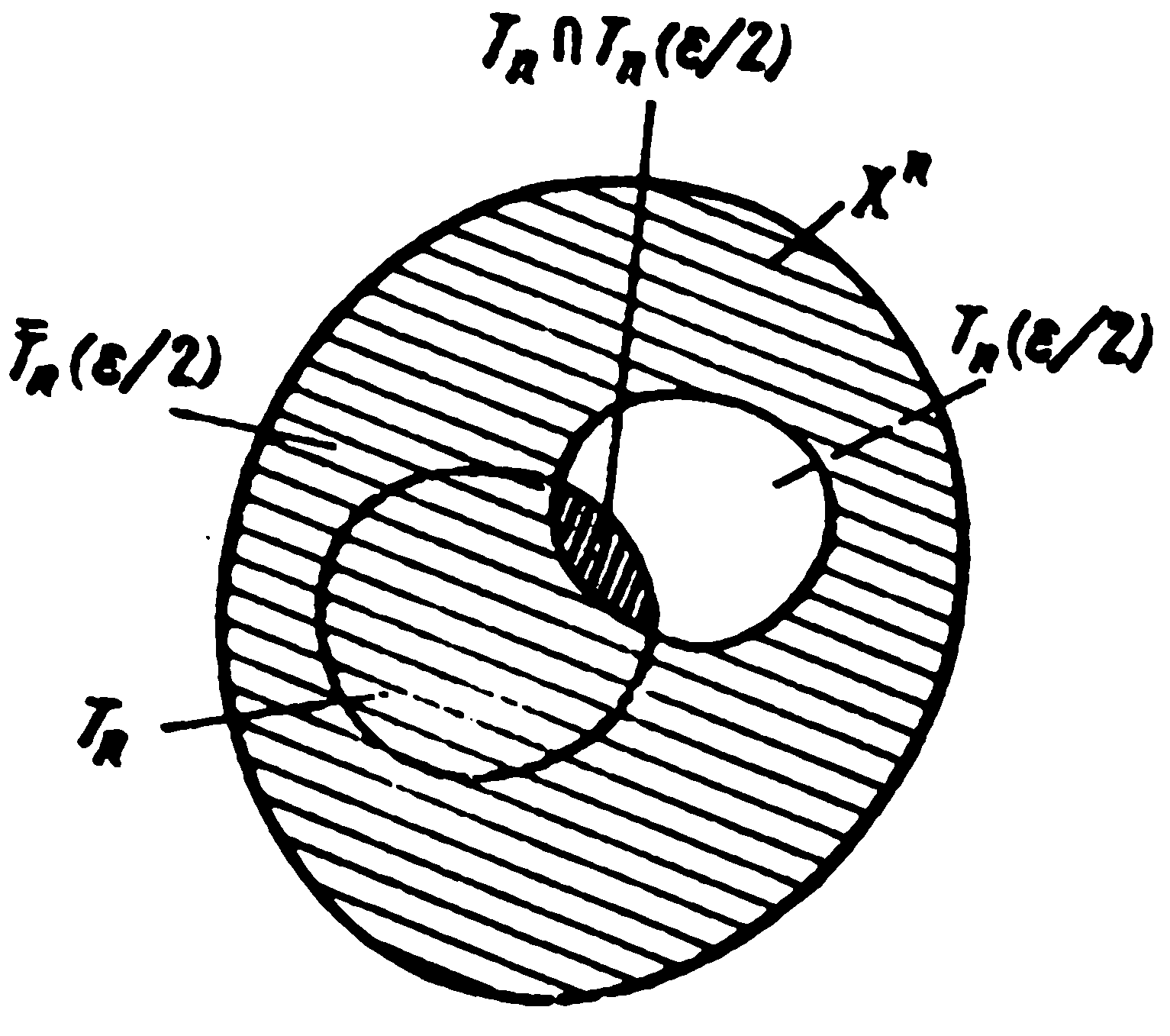 ис.2.2.
К доказательству обратной теоремы
кодирования
ис.2.2.
К доказательству обратной теоремы
кодирования
Рассмотрим теперь вероятность Рr(ТпТп(/2)). Для всякой последовательности х Тп (/2)Тп имеем р (х) 2 n[H(X) /2] , так как при этом хТп(/2). Число элементов в множестве ТпТп(/2) не превосходит |Тп |= 2nR, следовательно,
 (2.95)
(2.95)
Учитывая (2.94) и (2.95), из (2.93) получим (2.91).
Докажем теперь первое утверждение
теоремы. Для этого заметим что при R
< H(X)
множество
![]() не пусто при каждом п. Так как р(х)0
для всех хX,
то каждая последовательность хХп
имеет ненулевую вероятность. Следовательно
Для каждого конечного п найдется такое
(п) > 0 что Реп(п).
С другой стороны, в силу (1.8.2) найдется
такое N, что Для всех п>N
выполняется неравенствоРеп >
1/2. Полагая
не пусто при каждом п. Так как р(х)0
для всех хX,
то каждая последовательность хХп
имеет ненулевую вероятность. Следовательно
Для каждого конечного п найдется такое
(п) > 0 что Реп(п).
С другой стороны, в силу (1.8.2) найдется
такое N, что Для всех п>N
выполняется неравенствоРеп >
1/2. Полагая
=min {(1), (2), …, (N), ½},
получим, что для любого п и любого Тп
Реп > 0 (2.96)
Теорема доказана.
Таким образом, прямая и обратная теоремы кодирования показывают, что скорость создания информации при равномерном кодировании дискретного источника без памяти равна его энтропии. Этот вывод позволяет дать энтропии следующее толкование.
Представим себе, что источник подсоединен к некоторому устройству (кодеру источника), осуществляющему кодирование со скоростью R. Если кодовый алфавит содержит D символов, то в среднем на каждое сообщение источника будет появляться R/log D символов на выходе кодера. Для наилучшего кодера это количество будет весьма близким к Н(X)/logD. Следовательно, энтропия источника есть наименьшее количество двоичных символов на сообщение на выходе наилучшего двоичного кодера для этого источника при условии, что сообщения источника могут быть восстановлены по выходу кодера сколь угодно точно.
2.9. Эргодические дискретные источники
При рассмотрении дискретных источников
без памяти мы видели, что энтропия
источника представляет собой количество
информации, порождаемое источником в
единицу времени. Основанием для такого
вывода был закон больших чисел, из
которого вытекало, что собственная
информация в единицу времени
![]() с большой вероятностью близка к энтропии
H(X) при
больших п. В более общем случае, когда
сообщения источника не являются
независимыми, закон больших чисел может
оказаться неприменимым. Однако существует
широкий класс стационарных источников,
для которых величина
при больших п близка в вероятностном
смысле к энтропии на сообщение Н (Х|Х).
Это верно для так называемых эргодических
источников.
с большой вероятностью близка к энтропии
H(X) при
больших п. В более общем случае, когда
сообщения источника не являются
независимыми, закон больших чисел может
оказаться неприменимым. Однако существует
широкий класс стационарных источников,
для которых величина
при больших п близка в вероятностном
смысле к энтропии на сообщение Н (Х|Х).
Это верно для так называемых эргодических
источников.
Рассмотрим вначале множество из т одинаковых, не зависящих друг от друга стационарных источников. Пусть все источники рассматриваются на отрезке времени длины k и Xk — ансамбль сообщений для каждого источника. Рассмотрим функцию
I(x(k) | x(k 1) ,…, x(1) ) log p(x(k) | x(k 1) ,…, x(1) ) (2.97)
отображающую Xk в действительную ось. Для каждого источника эта функция представляет собой случайную величину, определенную на Xk. Так как предполагается, что источники независимы и одинаковы, то случайные величины Ii (x(k) | x(k 1) ,…, x(1)), i= 1, 2, ..., m, независимы и одинаково распределены.
Пусть
![]() (2.98)
(2.98)
— среднее арифметическое условной собственной информации сообщения x(k) для т источников. Математическое ожидание каждого слагаемого в сумме равно Н(X|Xkl). Поэтому по закону больших чисел для любых положительных и
Pr ( | Icp H (X | Xk1) | ) (2.99)
при достаточно больших m. Другими словами, средняя условная информация Iср, вычисленная по множеству источников (иногда говорят — по множеству реализаций, подразумевая, что каждый источник порождает одну реализацию последовательности сообщений), с большой вероятностью близка к условной энтропии H(X|Xk1) при больших т.
Рассмотрим теперь отрезки сообщений длины k на выходе какого-нибудь одного источника (или отрезки длины k одной реализации). Каждому отрезку x(i+l), ..., x(i+k) , i= 0, 1, ..., можно поставить в соответствие число
I(x(i+k) | x(i+k 1) ,…, x(i+1)) log p(x(i+k) | x(i+k 1) ,…, x(i+1)) (2.100)
— условную собственную информацию сообщения x(i+k). Среднее арифметическое этих информаций
![]() (2.101)
(2.101)
есть случайная величина, определенная на произведении k+т-1 ансамблей Х1 Х2 ... Хk+т-1. Величина Iср есть среднее арифметическое одинаково распределенных (в силу стационарности) случайных величин, которые не являются независимыми. Поэтому, вообще говоря, нет оснований полагать, что для любых положительных и
Pr ( | Icp H (X | Xk1) | ) (2.102)
при достаточно больших m. Если бы (1.9.6) действительно выполнялось, то
Рr(|Icp - Icp | 2 ) (2.103)
при достаточно больших т. В этом случае можно было бы утверждать, что среднее значение условных информаций, вычисленное по множеству источников, и среднее значение условных информаций, вычисленное по реализации одного источника, с большой вероятностью близки друг к другу при больших т.
Это рассмотрение можно обобщить, если на ансамбле Xk рассматривать произвольные функции (х(1),..., х(k)) и определять для них среднее по множеству источников аналогично (2.98) и среднее по одной реализации аналогично (2.101). Класс источников, для которых оба этих средних в вероятностном смысле близки независимо от выбора k и функции ( • ), носит название класса эргодических источников. Поэтому предположение (2.102) для эргодических источников выполняется.
Теперь дадим более строгое определение эргодических источников.
Пусть UX — стационарный источник, выбирающий сообщения из множества X, и ... x(1), x(0), х(1), х(2), ... — последовательность сообщений на его выходе. Пусть (х1 ..., xk) — произвольная функция, определенная на множестве Xk и отображающая отрезки сообщений длины k в числовую ось. Пусть
z(i) (x(i+1),…, x(i+k)), i=1,2,…, (2.104)
— последовательность случайных величин, имеющих в силу стационарности одинаковые распределения вероятностей. Обозначим через тz математическое ожидание случайных величин z(i).
Дискретный стационарный источник называется эргодическим, если для любого k, любой действительной функции (х1 ..., xk) М (•) < , определенной на Xk, любых положительных и найдется такое N, что для всех п>N
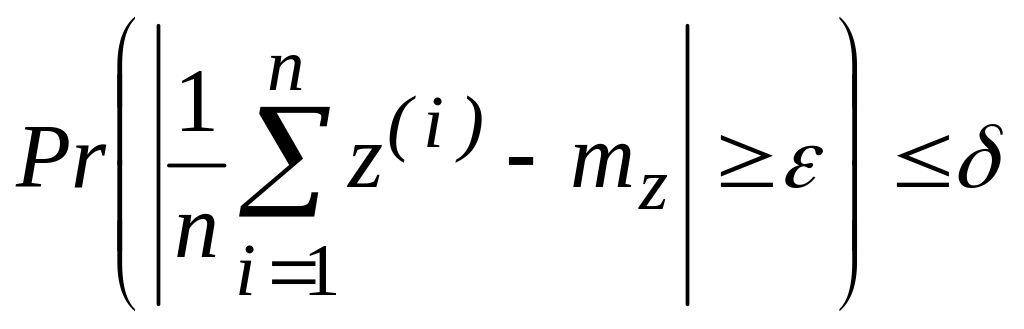 (2.105)
(2.105)
Пример 2.16. Если выбрать (x(1),..., x(k))= — log p( x(k) | x(k1),…, x(1)), то в случае дискретного эргодического источника предположение (2.102) будет выполняться.
Свойство эргодичности является весьма
полезным не только в теоретико-информационных
задачах. Благодаря эргодичности, многие
характеристики источников могут быть
найдены экспериментально с помощью
наблюдения, может быть достаточно
длительного, одной реализации
последовательности сообщений.
Действительно, наблюдая одну реализацию
и вычисляя по ней величины z(1),
..., z(n),
можно достаточно хорошо оценить величину
mz,
если в качестве оценки этой величины
брать среднее![]() .
Неравенство (2.105) показывает, что с
достаточно малой вероятностью, величину
которой можно задать заранее, оценка и
истинное значение будут отличаться
более чем на .
Следующий пример иллюстрирует одну из
таких задач оценивания.
.
Неравенство (2.105) показывает, что с
достаточно малой вероятностью, величину
которой можно задать заранее, оценка и
истинное значение будут отличаться
более чем на .
Следующий пример иллюстрирует одну из
таких задач оценивания.
Пример 2.17. Пусть дана реализация на выходе дискретного эргодического источника и требуется по этой реализации оценить вероятность, с которой источник порождает некоторое сообщение, например, x1X. Интуитивно ясно, что для этого достаточно подсчитать частоту появления этого сообщения в данной реализации. Однако точное обоснование того, почему нужно делать так, основано на применении свойства эргодичности. Положим k = 1 и
![]() (2.106)
(2.106)
Тогда М (x) = Рr(x=х1). Очевидно, есть частота появления сообщения х1 и (2.106) есть обоснование того, почему частота является хорошей оценкой вероятности.
Т е о р е м а Всякий дискретный стационарный источник без памяти является эргодическим.
Зафиксируем k и некоторую функцию (х1 ..., xk ) заданную на Xk, положим п = kl,
z (i) = (х(i),..., х (i+k1)), i=1,…,n
и рассмотрим сумму
![]() (2.107)
(2.107)
Где
![]() (2.108)
(2.108)
Заметим, что случайные величины z(i), i = 1, 2, ..., п, не являются независимыми, хотя сообщения рассматриваемого источника независимы. Однако случайные величины z((s1)k+j), s = 1, 2, ...,l, независимы, так как соответствующие им функции не имеют общих аргументов. Поэтому wj для каждого j есть сумма независимых одинаково распределенных случайных величин.
Используя (2.107), можно получить следующие соотношения:

Pr(![]() хотя бы при одном j)
(2.109)
хотя бы при одном j)
(2.109)
где
неравенство следует из того, что событие,
состоящее в том, что среднее арифметическое
k
величин больше ,
влечет событие, состоящее в том, что
хотя бы одно слагаемое в сумме больше
.
Поскольку случайные величины j,
j
— 1, ..., k,
одинаково распределены, то вероятности
—
![]() одинаковы для всех j
и, следовательно, правую часть (2.9.13)
можно оценить сверху величиной
одинаковы для всех j
и, следовательно, правую часть (2.9.13)
можно оценить сверху величиной
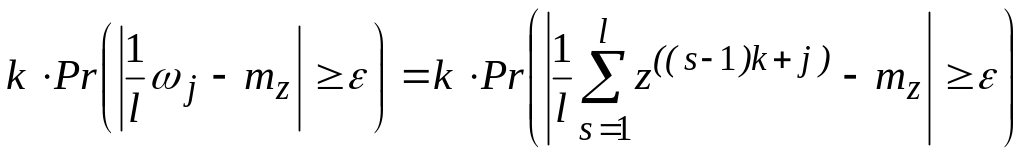 (2.110)
(2.110)
Случайные величины, стоящие под знаком суммы в (2.110), таковы, что можно применить закон больших чисел, согласно которому при достаточно большом l, а следовательно, при фиксированном k и достаточно большом n=kl, правая часть (2.110) будет не большей, чем любое заданное наперед положительное число . Теорема доказана.
В теореме показано, что стационарность и независимость являются достаточными условиями эргодичности. Метод доказательства теоремы подсказывает более слабое условие эргодичности. Используя этот метод, можно показать, что эргодичным является всякий дискретный стационарный источник, сообщения на выходе которого, разделенные интервалом в i, i N, единиц времени, независимы для некоторого ограниченного N.
Полезно разобрать пример стационарного неэргодического источника с тем, чтобы на этом примере более детально познакомиться с природой эргодичности.
Пример 2.18 Пусть имеются две урны. В первой урне лежат два белых и один черный шар. Во второй урне лежат два черных и один белый шар. Производится следующий эксперимент. Пусть случайно выбирается одна из двух урн, причем первая выбирается с вероятностью р. Затем из выбранной урны осуществляется последовательное извлечение шаров с возвращением. Экспериментатор подсчитывает число извлечений белого шара. Если в начале эксперимента выбрана первая урна, то частота появлений белого шара, зарегистрированная экспериментатором, будет равна 2/3, в противном случае — 1/3. Если имеется n независимо работающих экспериментаторов, то примерно nр из них зарегистрируют частоту 2/3, а примерно n(1—р) из них — частоту 1/3. Частота v появления белого шара в среднем по множеству всех экспериментаторов равна
![]() (2.111)
(2.111)
Если число р отлично от нуля или от единицы, то число v не совпадает с частотой, вычисленной по одной реализации (полученной одним экспериментатором). Следовательно, источник сообщений, соответствующий описанному эксперименту, не является эргодическим.
U
П
U1
 Выход
Выход

U2
Рис. 2.3. Неэргодический источник с двумя эргодическими компанентами
Структуру неэргодического источника примера 2.18 можно представить себе следующим образом (см. рис. 2 3) Имеются два эргодических (в данном примере — не имеющих памяти) источника U1, U2 и переключатель П, который может находиться в одном из двух положений. Переключатель случайно устанавливается в одно из положений при включении источника и остается в этом положении на протяжении всей работы. Экспериментатор имеет дело с одной реализацией на выходе источника, которой может соответствовать только одно положение переключателя. Наблюдая эту реализацию, экспериментатор не может вынести решение о том, с каким источником, эргодическим или нет, он имеет дело, так как ему недоступны другие возможные реализации. Можно показать, что всякий неэргодический источник можно представить в виде комбинации эргодических источников (эргодических компонент), аналогичной той, которая показана на рис. 2.3. В общем случае число компонент может быть большим, даже бесконечно большим.
Вернемся к рассмотрению количества информации, порождаемого эргодическим источником в единицу времени. Естественно ожидать, что это количество с большой вероятностью должно быть близким к энтропии на сообщение Н (Х|Х). Для того чтобы в этом убедиться, необходимо доказать, что для любых >0 и >0 найдется N такое, что при n > N
![]() (2.112)
(2.112)
На первый взгляд может показаться, что (2.112) прямо следует из определения эргодического источника. Однако это не так.
Информацию на сообщение можно представить следующим образом:
![]() (2 .113)
(2 .113)
Как легко видеть, под знаком суммы стоят случайные величины, полученные с помощью различных функций (•) (первое слагаемое является функцией одной переменной, второе —двух и т. д.), тогда как в определении эргодического источника (2.105) суммируются случайные величины, полученные с помощью одной и той же функции. Кроме того, Н(Х|Х) не является математическим ожиданием ни одного слагаемого под знаком суммы. Вместе с тем неравенство (2.112) справедливо для любого эргодического источника при достаточно большом n. Этот факт устанавливается в так называемой лемме Мак-Миллана.
Л е м м а (М а к -М и л л а н). Для любого дискретного эргодического источника любых, положительных и найдется N такое, что для всех n > N выполняется неравенство 2.112
Пусть р(х) = р(x(1),…, х(n) ), хXn, — распределение вероятностей для последовательностей сообщений дискретного стационарного эргодического источника. Определим для любого целого m, 1 m n, функцию
![]() (2.114)
(2.114)
Согласно
этому определению Q(х)
является аппроксимацией распределения
вероятностей р(х) источника, при которой
учитывается статистическая зависимость
каждого сообщения лишь от m
предшествующих ему сообщений.
Отметим, что
![]() .
Это легко проверяется суммированием
правой части (2.114) вначале по х(n),
затем по х(n1)
и в конце — по (х(1),...,
х(m)).
.
Это легко проверяется суммированием
правой части (2.114) вначале по х(n),
затем по х(n1)
и в конце — по (х(1),...,
х(m)).
Установим теперь простое свойство аппроксимирующего распределения Q(х), вытекающее из эргодичности. Покажем, что для любых >0 и >0 найдется N такое, что для всех n>N имеет место неравенство
![]() (2.115)
(2.115)
Для
того чтобы это доказать, заметим, что
для любых двух случайных величин
![]() и
и
![]() и любого >0
имеет место неравенство
и любого >0
имеет место неравенство
![]() (2.116)
(2.116)
которое
следует из того, что если |![]() +
|
,
либо |
|
,
либо |
|
.
Заметим также, что
+
|
,
либо |
|
,
либо |
|
.
Заметим также, что
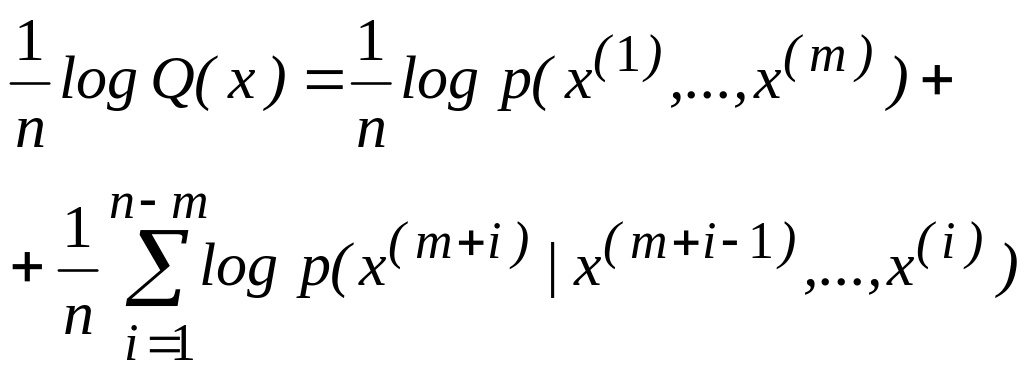 (2.117)
(2.117)
Так как
![]()
для всех i, то согласно предположению об эргодичности для любых >0 и >0 найдется N такое, что для всех n>N
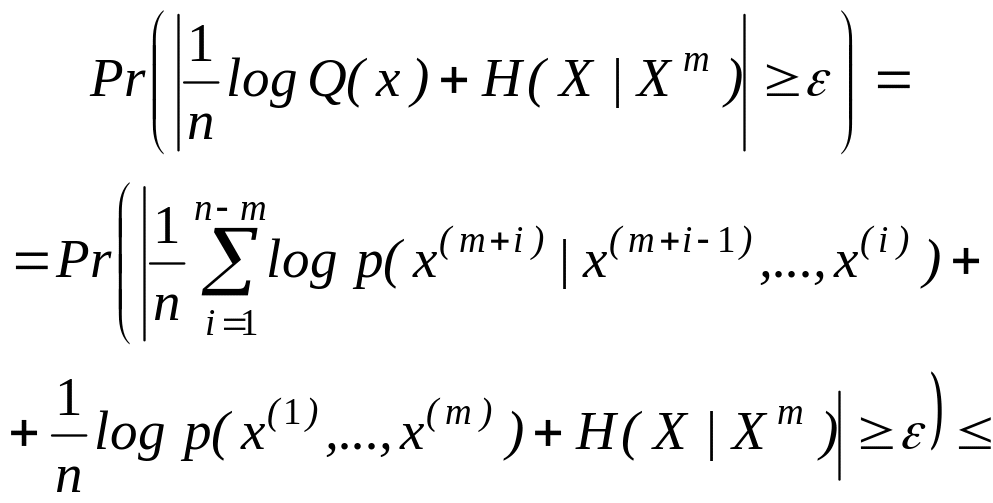

где первое неравенство — следствие неравенства (2.116), а второе — следствие эргодичности и того, что log р(х(1),…, х(m)) принимает ограниченные значения с вероятностью 1. Таким образом, утверждение, связанное с неравенством (2.115), доказано.
Покажем далее, что распределение Q(х) достаточно хорошо аппроксимирует исходное распределение р(х), а именно, что для любых >0 и >0 найдется такое N, что при достаточно большом m для всех n>N выполняется неравенство
![]() (2.118)
(2.118)
Для доказательства этого утверждения воспользуемся неравенством Чебышева. Имеем
![]() (2.119)
(2.119)
Чтобы оценить математическое ожидание, стоящее в правой части этого неравенства, применим неравенство для логарифма согласно которому можно записать, что log х log е для все х0, и, следовательно,
|log х| 2х log е — log х (2.120)
Неравенство (2.120) легко проверяется посредством отдельного рассмотрения случаев х 1 и х < 1. Отсюда следует, что
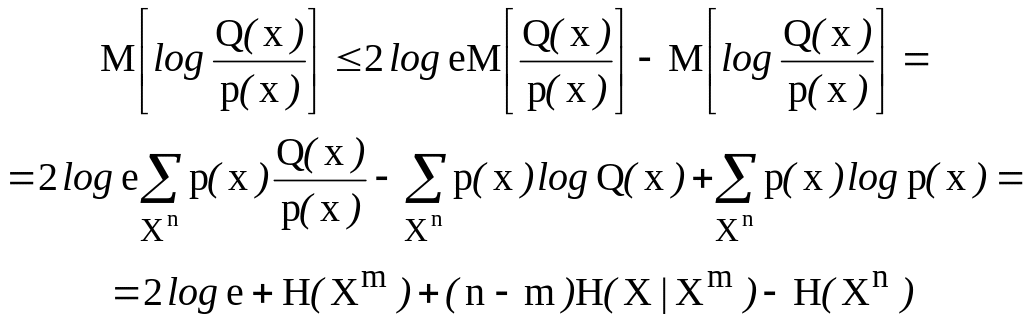
и из (2.119) вытекает, что
![]() (2.121)
(2.121)
Из теорем следует, что при любых фиксированных и , при достаточно большом, но фиксированном m, правая часть неравенства (2.121) стремится к нулю при n. Поэтому найдется N такое, что при всех n>N будет выполняться неравенство q .
Для завершения доказательства леммы следует показать, что для любых >О и >О найдется N такое, что при n >N
![]()
Для заданных и выберем m и N такими большими, чтобы при всех n>N выполнялись неравенства
q /2
| H ( X | X m) H ( X | X )| /3
![]()
Тогда из утверждений, связанных с неравенствами (2.115) и (2.118), будет следовать, что
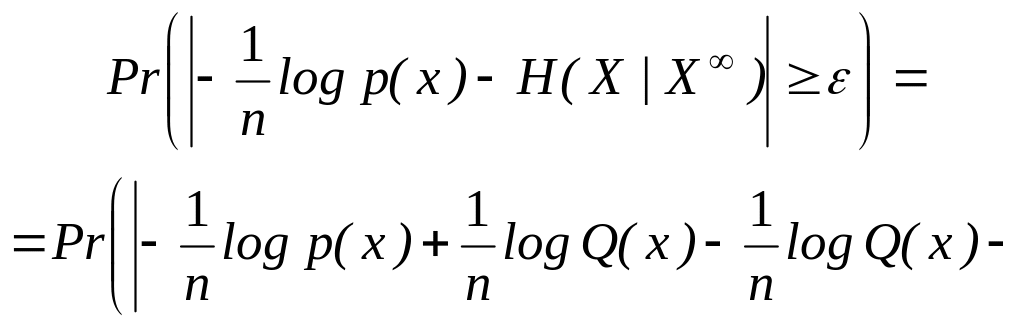
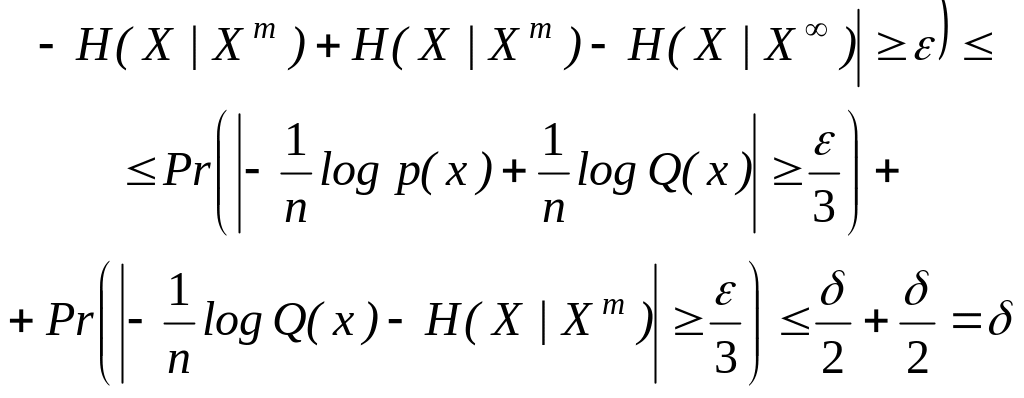
Лемма доказана.
Из леммы Мак-Миллана может быть легко выведена теорема о высоковероятных множествах, а также прямая и обратная теоремы кодирования при равномерном кодировании дискретного эргодического источника.
Т е о р е м а (теорема о высоковероятных множествах). Пусть UХ — дискретный эргодический источник, и {Хn, р(х)}, n = 1, 2, ..., — ансамбли последовательностей длины n на его выходе. Пусть Н (X|Х) — энтропия на сообщение и — некоторое положительное число. Пусть Тn() — подмножество множества Xn, определенное для каждого n следующим образом:
![]() (2.122)
(2.122)
где I (х) = — log р (х) — собственная информация последовательности хХn. Тогда для любых >0 и >0 найдется N такое, что для всех п > N выполняются следующие неравенства:
Pr ( x Тn ( )) 1 (2.123)
![]() (2.124)
(2.124)
Т е о р е м а (прямая теорема кодирования). Пусть R>H(X|X), тогда для любого положительного существует код со скоростью R, который кодирует дискретный эргодический источник с вероятностью ошибки, не превышающей .
Т е о р е м а (обратная теорема кодирования). Пусть R<H(X|X), тогда существует зависящее от R положительное число такое, что для каждого кода со скоростью R, кодирующего дискретный эргодический источник, вероятность ошибки не меньше . Более того, для любой последовательности кодов со скоростью R
![]() (2.125)
(2.125)
где Рen — вероятность ошибки для кода, кодирующего отрезки сообщений длины п.
Доказательства прямой и обратной теорем практически не отличаются от доказательств соответствующих теорем для дискретных источников без памяти.
Из этих теорем следует, что скорость создания информации дискретным эргодическим источником при равномерном кодировании равна его энтропии на сообщение H(X|X). Это утверждение позволяет дать такое же толкование энтропии на сообщение для эргодических источников, как энтропии для постоянных источников: и то и другое есть наименьшее количество двоичных символов, приходящихся на одно сообщение на выходе наилучшего двоичного кодера, при условии, что сообщения могут быть восстановлены по выходу кодера сколь угодно точно.
2.10. Постановка задачи неравномерного кодирования дискретных источников. Коды с однозначным декодированием
В предыдущих параграфах мы познакомились с задачей равномерного кодирования дискретных источников и показали, что при таком кодировании скорость создания информации равна энтропии источника на сообщение. Здесь будет рассмотрен другой подход к задаче кодирования.
Для того чтобы его пояснить, вернемся к примеру 2.6.4. В этом примере были разобраны два метода кодирования телеграмм. Один метод, так называемый метод побуквенного кодирования, позволяет закодировать и затем безошибочно декодировать любую телеграмму, затрачивая на одну букву 6 двоичных символов. Второй метод оказался ключевым для задачи равномерного кодирования. Он позволяет однозначно кодировать не все телеграммы, а только некоторые типичные для данного источника. При таком кодировании на одну букву будет затрачиваться примерно 13/8 двоичных символов — существенно меньше, чем при побуквенном кодировании.
При кодировании телеграмм есть еще один метод кодирования, о котором не было ничего сказано раньше. Предположим, что известно, с какими вероятностями появляются те или другие буквы в телеграммах. Тогда можно использовать неравномерный код, в котором длины кодовых слов подобраны так, что часто встречающиеся буквы кодируются относительно короткими двоичными словами, а редкие —длинными. При таком способе побуквенного кодирования, использующем неравномерные коды, любая телеграмма может быть однозначно закодирована и однозначно декодирована, а среднее количество двоичных символов на букву может быть сделано меньшим, чем в случае равномерного побуквенного кодирования.
Как
и для любого метода кодирования источника,
основной характеристикой неравномерного
кодирования является количество
символов, затрачиваемых на кодирование
одного сообщения. В случае равномерного
кодирования это количество одно и то
же для любого сообщения источника.
Действительно, каждый отрезок из n
сообщений при равномерном кодировании
отображается в последовательность
![]() D-ичных
кодовых символов, представляющую собой
D-ичную
запись номера кодируемого отрезка. При
неравномерном кодировании это не так.
Количество символов, затрачиваемых при
кодировании, зависит от сообщений
источника и поэтому представляет собой
случайную величину. В этом случае
разумной мерой качества кодирования
является среднее количество символов
на сообщение.
D-ичных
кодовых символов, представляющую собой
D-ичную
запись номера кодируемого отрезка. При
неравномерном кодировании это не так.
Количество символов, затрачиваемых при
кодировании, зависит от сообщений
источника и поэтому представляет собой
случайную величину. В этом случае
разумной мерой качества кодирования
является среднее количество символов
на сообщение.
Обозначим через mi длину слова, кодирующего сообщение xiX. Пусть р (xi) — вероятность этого сообщения, тогда
![]() (2.126)
(2.126)
будет
средней длиной кодовых слов, кодирующих
ансамбль сообщении {Х, р(х)}. Предположим,
что неравномерный код используется для
кодирования отрезков сообщений длины
n,
т. е. для кодирования ансамбля {Хn,
р (х)}, где р(х) — распределение вероятностей
на Хn,
задаваемое с помощью задания источника.
Пусть
![]() — средняя длина кодовых слов.
— средняя длина кодовых слов.
Число
![]() (2.127)
(2.127)
называется средней скоростью неравномерного кодирования посредством D-ичного кода при разбиении последовательности сообщений на блоки длины п. Средняя скорость неравномерного кодирования измеряется в двоичных символах на сообщение.
Пример 2.19 Предположим, что n = 1 и источник порождает в каждый момент времени одно из восьми сообщений х1, ..., х8. Вероятности сообщений приведены во втором столбце табл. 2.10.1.
Заметим, что энтропия ансамбля сообщений этого примера равна 2,75 бит. В таблице приведены два двоичных кода — равномерный и неравномерный, которые однозначно кодируют указанное множество сообщений. Для первого кода все слова имеют одинаковую длину, равную 3. Для второго — слова имеют различные длины и, как нетрудно подсчитать средняя длина равна 2,75 символов (совпадение с энтропией неслучайно). Оба кода осуществляют побуквенное кодирование. Скорость кодирования в первом случае равна 3 бит/сообщение, а во втором — 2,75 бит/сообщение.
Таблица 2.1
xi |
p(xi) |
Равномерный код |
Неравномерный код |
mi |
x1 |
1/4 |
000 |
00 |
2 |
x2 |
1/4 |
001 |
01 |
2 |
x3 |
1/8 |
010 |
100 |
3 |
x4 |
1/8 |
011 |
101 |
3 |
x5 |
1/16 |
100 |
1100 |
4 |
x6 |
1/16 |
101 |
1101 |
4 |
x7 |
1/16 |
110 |
1110 |
4 |
x8 |
1/16 |
111 |
1111 |
4 |
Средняя скорость неравномерного кодирования зависит от выбора n и множества кодовых слов. Наша цель состоит в определении наименьшей достижимой средней скорости. Прежде чем перейти к решению этой задачи, необходимо ответить на следующий вопрос: любой ли неравномерный код пригоден для кодирования сообщений источника, и если нет, то какие ограничения на него должны быть наложены? Покажем существо этого вопроса следующим примером.
Пример 2.20. Предположим, что источник порождает сообщения х1, х2, х3, х4 и эти сообщения кодируются следующим образом: х10, х201, х310, х4011. Кодовый алфавит состоит из двух символов 0 и 1. Пусть на выходе источника появилась следующая последовательность сообщений х2 х3 х2 х1… Кодер вырабатывает для каждого сообщения свое кодовое слово. На его выходе возникает последовательность 0110100... Нет специального разделительного знака пробела между словами. Если бы он был, то следовало бы рассматривать кодовый алфавит, состоящий из 0, 1 и пробела, что привело бы к задаче кодирования с кодовым алфавитом из трех символов. Декодеру известно лишь начало указанной выше двоичной последовательности, но неизвестно, с какого символа начинается второе кодовое слово, третье и т. д. Оказывается, что эта последовательность допускает несколько различных способов декодирования: (х2 х3 х2 х1...) — правильное декодирование, (х4 х2 х1 х1 ...), (х4 х1 х3 х1...) — неправильные декодирования. В этом примере причиной неоднозначности декодирования является то, что кодовое слово 0 является началом слова 01, а это слово в свою очередь является началом слова 011. Коды примера 2.19 позволяют декодировать однозначно. Для равномерного кода это так потому, что; все слова имеют одинаковую длину; последовательно отсчитывая по три символа, мы будем получать кодовые слова. Для неравномерного кода примера 2.19 ни одно слово не является началом другого, и поэтому разбиение на кодовые слова происходит однозначно.
Коды, в которых ни одно слово не является началом другого, называются префиксными. Коды, в которых любая последовательность кодовых слов допускает однозначное разбиение на кодовые слова, называются кодами со свойством однозначного декодирования. Префиксные коды являются кодами со свойством однозначного декодирования, но не наоборот.
Пример 2.21. Код, образованный словами 0, 01, 011, не является префиксным, но является однозначно декодируемым. Покажите это самостоятельно.
Таким образом, для кодирования сообщений источника пригодны только те коды, которые допускают однозначное декодирование.
Скоростью создания информации дискретным источником при неравномерном кодировании называется наименьшее число Н такое, что для любого R>Н найдется n (длина кодируемых сообщений) и неравномерный код со средней скоростью кодирования R, который допускает однозначное декодирование.
Ниже мы покажем, что скорость создания информации при неравномерном кодировании совпадает со скоростью создания информации при равномерном кодировании и равна энтропии источника на сообщение.
Для того чтобы доказать, что число Н есть скорость создания информации при неравномерном кодировании, нужно как и раньше, доказывать прямую и обратную теоремы. Первая из них будет утверждать, что для всех R >Н найдется n и однозначно декодируемый неравномерный код со средней скоростью R, а вторая будет утверждать, что для любого R < H не существует однозначно декодируемого кода ни при каком n.
Прежде чем приступить к детальному изучению задачи неравномерного кодирования, докажем теорему, в которой формулируется необходимое условие того, чтобы код был однозначно декодируем.
Т е о р е м а Предположим, что однозначно декодируемый код состоит из М слов, длины которых равны т1,…,тM и кодовый алфавит содержит D символов.
![]() (2.128)
(2.128)
Пусть L — произвольное положительное целое число. Имеет место следующее равенство:
![]() (2.129)
(2.129)
Заметим,
что в выражении, стоящем в правой части
равенства (2.129), каждое слагаемое
соответствует каждой возможной
последовательности из L
кодовых слов. Сумма
![]() равна суммарной длине соответствующей
последовательности кодовых слов. Если
через Aj
обозначить число последовательностей
из L
кодовых слов, имеющих суммарную длину
j,
то (2.129) можно переписать следующим
образом:
равна суммарной длине соответствующей
последовательности кодовых слов. Если
через Aj
обозначить число последовательностей
из L
кодовых слов, имеющих суммарную длину
j,
то (2.129) можно переписать следующим
образом:
![]() (2.130)
(2.130)
где m — максимальное из чисел т1,…,тM. Код однозначно декодируем, если при любом L и любом j имеется единственная последовательность кодовых символов длины j, образованная L кодовыми словами. Так как Dj — максимальное количество различных последовательностей длины j, то Aj Dj. Подставляя это неравенство в (2.130), получим
![]() (2.131)
(2.131)
Или
![]() (2.132)
(2.132)
Неравенство (2.132) справедливо при всех положительных целых L. Переходя к пределу при L , получим утверждение теоремы.
Таким образом, мы получили необходимое условие того, чтобы код обладал свойством однозначного декодирования. Ниже будут изучены коды, для которых легко показать, что это условие является также достаточным.
2.11. Кодовые деревья. Неравенство Крафта
Как было сказано выше, префиксные коды обладают свойством однозначного декодирования. В таких кодах ни одно кодовое слово не является началом другого. Удобное описание префиксных кодов дают специальные графы, называемые деревьями (или кодовыми деревьями). D-ичным деревом называется граф, т. е. такая система узлов и связывающих их ребер, в котором нет петель или замкнутых путей и в котором из каждого узла выходит не более D ребер и в каждый узел, кроме одного (корня дерева), входит точно одно ребро. Каждому из ребер, выходящих из узла, сопоставляется один символ кодового алфавита, содержащего D символов, причем различным ребрам, выходящим из одного узла, сопоставляются различные символы. На рис. 2.4 показаны двоичные кодовые деревья, соответствующие кодам примеров 2.19. Под рисунком дерева показано правило сопоставления ребер и двоичных символов: каждому правому ребру сопоставляется 1, каждому левому — 0. На рис. 2.5 приведен пример троичного дерева, соответствующего троичному коду 00, 01, 02, 10, 11, 12, 20, 210, 220, 221, 222.
Для доказательства следует показать, что условие (2.11.1) является необходимым и достаточным условием существования дерева, концевые узлы которого имеют порядки т1,…,тM.