1. Дискретная модель жесткой нити

В качестве расчетной схемы реальной нити принимается цепь, состоящая из отдельных, соединенных между собой элементов с упругими вставками. Масса элементов и все нагрузки приводятся в узлы (рис. 1).

Рис. 1

Уравнения равновесия узлов и элементов цепи имеют вид [1]

	(1.1)
	(1.2)
,	(1.3)

где , 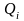‑ продольная и поперечная силы в -м элементе цепи, ‑ изгибающий момент в - м узле, - угол наклона - го элемента к оси , ‑ длина элемента цепи,

‑ начальная длина заготовки нити, ‑ координаты -го узла.

Считаем, что материал стержней линейно-упругий. Абсолютное удлинение элемента цепи пропорционально продольной силе, а изгибающий момент пропорционален кривизне (закон Гука)

,	(1.4)
	(1.5)

В формулах (1.4), (1.5) введены следующие обозначения: ‑ модуль упругости материала, 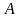‑ площадь, ‑ момент инерции поперечного сечения элемента цепи.

Обозначим через длину элемента цепи в результате продольной деформации. Тогда выражение для продольной силы можно представить в виде

.

(1.6)

Длину -го элемента цепи выразим через координаты узлов:

.

(1.7)

Направляющие косинусы элемента цепи определяться по формулам:

,

(1.8)

После подстановки (1.6) и (1.8) в уравнения (1.1), (1.2) получим

,	(1.9)
	(1.10)

Если в уравнениях (1.9), (1.10) изгибную жесткость положить равной нулю (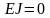 ), то получим уравнения нелинейных колебаний гибкой нити [2].

Подстановка выражений для изгибающего момента (1.5) в уравнение равновесия элемента (1.3) дает

.

(1.11)

В уравнениях (1.9) заменяем слагаемые, содержащие поперечную силу по формулам (1.11). В результате получаем

.

(1.12)

Аналогичная замена в уравнениях (1.10) дает

(1.13)

После подстановки выражений для направляющих косинусов элементов цепи (1.8) в уравнения (1.12), (1.13) получим систему нелинейных дифференциальных уравнений относительно неизвестных координат узлов цепи , ( ). Полученные уравнения описывают нелинейные колебания дискретной модели жесткой нити.

Если в уравнениях (1.12), (1.13) (записанных через координаты узлов цепи) силы инерции положить равными нулю, то приходим к системе 2(n-1) нелинейных уравнений статики жесткой нити с симметричной и положительно определенной матрицей Якоби.

Отметим, что нелинейные уравнения статики для дискретной модели жесткой нити, но записанные в усилиях, были получены в работе [3]. Неизвестными в этих уравнениях являлись проекции на координатные оси усилий в элементах цепи и безразмерные величины . Методом начальных параметров уравнения были сведены к системе трех нелинейных уравнений. В качестве неизвестных были приняты проекции на координатные оси усилий в первом элементе цепи , и величина , связывающая отношение поперечной и продольной сил.

Результаты сравнительных расчетов по двум описанным выше алгоритмам показали хорошее совпадение.

Отметим, что уравнения (1.12), (1.13) (в перемещениях) могут быть использованы для описания работы нитевых моделей упругого основания [4]. Для этого в уравнениях (1.13) необходимо ввести слагаемые , суть которых – реакции в упругих опорах, моделирующих основание.

Если упругие опоры сопротивляются только сжатию, то получим уравнения, описывающие колебаний жесткой нити на одностороннем упругом основании. Такая расчетная схема может применяться при исследовании колебаний трубопроводов, заглубленных в грунт.

Решение отдельных задач статики плоских стержневых систем с односторонними связями приведено в [5]. В работе [6] показано использование гибких нитей в качестве односторонних связей.
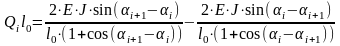