Матрица стандартизованных рангов

Оцениваемые объекты	Эксперты						Ri	i		i
	1	2	…	j	…	n
1	r11	r12	…	r1j	…	r1n	R1	1		1
2	r21	r22	…	r2j	…	r2n	R2	2		2
…	…	…	…	…	…	…	…	…	…	…
i	ri1	ri2	…	rij	…	rin	Ri	i		i
…	…	…	…	…	…	…	…	…	…	…
m	rm1	rm2	…	rmj	…	rmn	Rm	m		m
Тi	Т1	Т2	…	Тj	…	Тn	Ri		S(2)

Задача построения обобщенной оценки объектов, если эксперты использовали количественную шкалу, заключается в определении среднего значения или медианы оценки. При измерении в порядковой шкале методом ранжирования и индивидуальных оценок экспертов обобщение оценок производится нахождением суммарного ранга и относительной значимости каждого объекта.

Оценки, полученные в результате обработок, являются случайными величинами, поэтому необходимо определение их достоверности.

Сумма рангов (абсолютная значимость) по каждому объекту

R_i = ,

где r_ij – ранг (место) i–го объекта у j–го эксперта.

Средняя сумма рангов

= или = .

Сумма квадратов отклонений суммарных рангов от средней суммы рангов

S(²) = = ,

где _i – отклонение суммарных рангов от средней суммы рангов.

Показатель связанных рангов в j–й ранжировке

T_j = ,

где H_j – число групп равных рангов в j–й ранжировке;

h_k - число равных рангов в k–й группе связанных рангов при ранжировке j–м экспертом.

Если совпадающих рангов нет, то h_k = 0 и T_j = 0.

Степень согласованности мнений экспертов при наличии совпадающих рангов определяется величиной коэффициента конкордации Кендалла.

W =

где m – общее количество оцениваемых факторов; n – общее количество экспертов, участвующих в оценке значимости факторов.

Коэффициент конкордации изменяется от 0 до 1, причем, если W = 0, согласованность мнений экспертов отсутствует, а если W = 1, все эксперты придерживаются одинакового мнения.

Коэффициент конкордации позволяет определить, - существует ли неслучайная согласованность во мнениях экспертов. Чем ближе значение W к 1, тем выше будет степень неслучайной согласованности.

Значимость полученного коэффициента конкордации обычно оценивается по критерию χ² – ХИ-квадрат.

χ² = n  (m -1)  W = .

Полученное расчетное значение критерия χ² сравнивается с табличным. Если > , то можно утверждать при уровне доверительной вероятности p = 1 – , что имеется неслучайно согласованность мнений экспертов по ранжировке объектов (например, факторов, существенных для моделирования структур производственных систем). Табличное значение критерия χ² определяется по таблицам квантилей χ² – распределения в столбце, соответствующем уровню достоверности  = 1 – p (обычно  принимается равным 1% или 5%), в строке, соответствующей числу степеней свободы ν = m –1 (количество оцениваемых объектов без одного).

Относительная значимость оцениваемых объектов

_i = = .

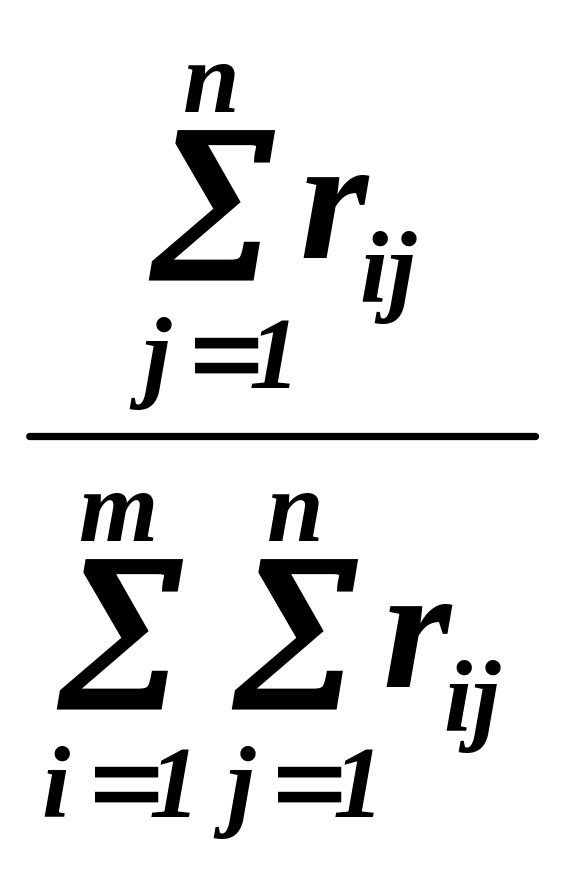Диаграмма значимости оцениваемых объектов может быть построена по показателям абсолютной R_i или относительной _i значимости. Диаграмма наглядно показывает важные объекты и те, которыми можно пренебречь.

Пусть для оценок качества продукции предлагается использовать следующие показатели: Х₁ – уровень обработки изделия, Х₂ – качество материалов, Х₃ – прогрессивность модели, Х₄ – стоимость изделия, Х₅ – функциональность изделия, Х₆ – выразительность фирменного знака и совершенство упаковки. С помощью опроса 10 экспертов необходимо выбрать три наиболее существенных показателя.

Экспертные оценки, преобразованная матрица рангов, все необходимые расчеты и графические построения представлены в табл. 3, табл. 4 и на рис. 1. Наиболее значимыми показателями являются 3-й, 1-й и 2-й.

При обработке экспертной информации может быть использован подход к определению коэффициентов компетентности экспертов, основанный на нормированных балльных оценках. Таблица нормированных балльных оценок для каждого эксперта строится путём деления каждого балла на суммарный балл для данного эксперта (табл. 8):

5/18=0,278; 4/18=0,222; 3/18=0,167; 2/18=0,111; 1/18=0,056;

(0,167+0,176+0,286+0,118+0,211+0,176+0,278+0,176+0,239+

+0,211)/10=0,203.

Таблица 8

Результаты опроса мнений экспертов

Показатели	Специалисты											2		V
	1	2	3	4	5	6	7	8	9	10
1	3	3	4	2	4	3	5	3	4	4	3,5	0,72	0,85	0,24
2	4	3	2	4	2	3	3	4	3	4	3,2	0,68	0,82	0,26
3	5	5	4	5	5	5	4	5	4	5	4,7	0,23	0,48	0,1
4	1	3	1	2	2	3	1	2	2	3	2,0	0,67	0,82	0,41
5	2	1	2	3	4	1	2	2	3	1	2,1	0,99	0,99	0,47
6	3	2	1	1	2	2	3	1	1	2	1,8	0,62	0,79	0,44
	18	17	14	17	19	17	18	17	17	19	Суммарный балл

Взвешенные суммы относительных балльных оценок определяются путём суммирования нормированных баллов для каждого эксперта, предварительно умноженных на средние баллы характеристик:

0,167٠0,203+0,222٠0,185+0,278٠0,272+0,056٠0,115+0,111٠0,122=0,188.

Таблица 9

Оценка компетентности экспертов

Средние баллы характеристик	Нормированные балльные оценки для экспертов по оцениваемым характеристикам 1 2 3 4 5 6 7 8 9 10
0,203	0,167	0,176	0,286	0,118	0,211	0,176	0,278	0,176	0,235	0,211
0,185	0,222	0,176	0,143	0,235	0,105	0,176	0,167	0,235	0,176	0,211
0,272	0,278	0,294	0,286	0,294	0,263	0,294	0,222	0,294	0,235	0,263
0,115	0,056	0,176	0,071	0,118	0,105	0,176	0,056	0,118	0,118	0,158
0,122	0,111	0,059	0,143	0,176	0,211	0,059	0,111	0,118	0,176	0,053
Сумма взвешенных оценок	Взвешенные суммы относительных балльных оценок
1,883	0,188	0,188	0,195	0,189	0,182	0,188	0,185	0,193	0,186	0,189
	Коэффициенты компетентности экспертов
	0,1	0,1	0,104	0,1	0,097	0,1	0,098	0,103	0,099	0,1

Коэффициенты компетентности экспертов определяются как отношения взвешенных сумм относительных балльных оценок к сумме взвешенных оценок:

0,188+0,188+0,195+0,189+0,182+0,188+0,185+0,193+

+0,186+0,189=1,883;

0,188 / 1,883 = 0,1 и т.д.

Таким образом, эксперт, у которого оценки ближе к среднегрупповым, полагается самым компетентным.

Матрица исходных экспертных оценок подвергается обработке и преобразуется в матрицу нормальной ранжировки так, чтобы сумма рангов в каждом столбце равнялась значению (m+1)•m/2, где m-число ранжируемых характеристик. Для этого расставим ранги (места), занимаемые оценками, в порядке их возрастания, причем ранжируемым параметрам, получившим одинаковые оценки, приписываются значения рангов, равные среднему арифметическому значению мест, которые они делят между собой. Например, для оценок "1", "2", "4" и "5" первого столбца значения мест составят 1, 2, 5 и 6 соответственно, а для оценок "3" этого же столбца среднеарифметическое значение мест будет равно (3+4)/2=3,5, поскольку таких оценок – две, и они делят между собой 3 и 4 места. Следовательно, этим оценкам будет соответствовать ранг 3,5.

Стандартизованные значения рангов вносятся на соответствующие места в матрицу (табл. 10).

Средняя сумма рангов:

или

где m - число ранжируемых параметров; n - число экспертов;

r_ij - место ранга i-го параметра у j-го эксперта.

Показатель повторяемости для 2-го столбца рассчитывается следующим образом: число повторений оценок составит 3, 1, 1, 1, тогда T₄ = (3³ – 3 + 1³ – 1 + 1³ – 1+ 1³ – 1)/12=2.

Определим степень согласованности мнений экспертов

W = = .

Таблица 10