1.4. Применение формул Эйлера и Муавра

Если в формуле Эйлера (1.2) заменить на , то Складывая эти равенства, получим: Вычитая, будем иметь:

иметь: .

Этими формулами пользуются для выражения степеней и и их произведений через синус и косинус кратных дуг.

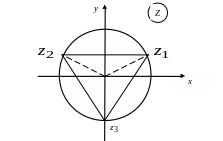
Рис. 3

Пример.

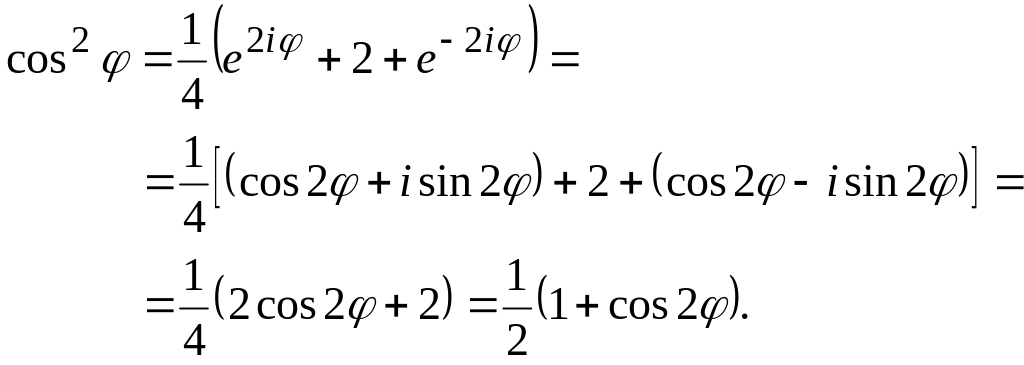
Пример.

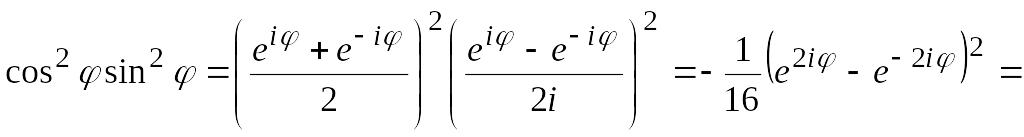
Рассмотрим теперь формулу Муавра. Если положить в ней , то получится:

Эта формула используется для выражения синуса и косинуса кратных дуг через степени синуса и косинуса.

Пример. При получим: Возведя левую часть в куб, имеем:

Используя определение равенства двух комплексных чисел, находим:

1.5. Многочлены в комплексной области

Определение. Многочленом или целой рациональной функцией от x называется функция , где n - целое положительное число. Коэффициенты действительные или комплексные числа.

Независимая переменная x может принимать как действительные, так и комплексные значения. Корнем многочлена называется такое значение переменной , при котором многочлен обращается в нуль: .

Для многочлена имеет место

Теорема Безу. При делении многочлена на разность получается остаток, равный .

Доказательство. При делении многочлена на частным будет многочлен , степень которого будет на единицу ниже степени . Остатком будет являться постоянное число R. То есть можно записать: Это равенство справедливо при всех , так как деление на при не имеет смысла. Перейдем к пределу в этом равенстве при . Предел левой части равен , а предел правой равен R. То есть

Следствие. Если - корень многочлена , то есть , то делится без остатка на и, следовательно, представляется в виде произведения , где - многочлен степени на единицу ниже степени .

Пример. Многочлен при обратится в нуль . Поэтому он делится без остатка на :

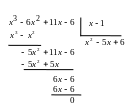
То есть представляется в виде произведения: Возникает вопрос: всякий ли многочлен имеет корни? Ответ на него дает

Основная теорема алгебры. Всякий многочлен n-ой степени (целая рациональная функция) имеет по крайней мере один корень, действительный или комплексный.

Пользуясь основной теоремой алгебры, легко доказать следующее.

Следствие. Всякий многочлен n-ой степени разлагается на n линейных множителей вида и множитель, равный коэффициенту при .

Доказательство. Пусть дан многочлен степени n: В силу основной теоремы алгебры этот многочлен имеет по крайне мере один корень, действительный или комплексный, который обозначим через . На основании следствия из теоремы Безу делится на , без остатка и можно записать: , где - многочлен - ой степени. Многочлен по основной теореме алгебры также имеет корень, который обозначим через . По следствию из теоремы Безу, , где - многочлен - ой степени. Аналогично . Продолжая этот процесс выделения линейных множителей, дойдем до соотношения , где - многочлен нулевой степени, то есть некоторое действительное число. На основании полученных равенств можно записать: . С учетом выражения для получим, что равняется коэффициенту при , то есть . Поэтому окончательно имеем:

(1.4)

Из этого разложения следует, что числа -корни многочлена , так как при подстановке правая часть (1.4), а следовательно, и левая, обращается в нуль. Никакое значение , отличное от не может быть корнем многочлена , так как ни один из множителей в правой части (1.4) не обращается в нуль при . Отсюда следует важный

Вывод. Многочлен n - ой степени не может иметь более n различных корней. Если в разложении (1.4) многочлена на линейные множители некоторые линейные множители окажутся одинаковыми, то их можно объединить. Тогда разложение на множители будет иметь вид:

(1.5)

При этом: В этом случае корень называется корнем кратности или - кратным корнем, - корень кратности и т.д. Если какое-либо , то корень называется корнем кратности один или простым корнем многочлена . Если многочлен имеет корень a кратности k, то мы будем считать, что многочлен имеет k одинаковых корней. Отсюда можно сделать окончательный

Вывод. Всякий многочлен n-ой степени имеет ровно n корней (действительных или комплексных).

Рассмотрим теперь многочлен , имеющий действительные коэффициенты . Для него имеет место формула (1.4), где корни могут быть как действительными, так и комплексными. Имеет место следующая

Теорема. Если многочлен с действительными коэффициентами имеет комплексный корень , то он имеет и сопряженный корень .

Доказательство. Подставим в многочлен значение , произведем возведение в степень, умножение на коэффициенты и приведем подобные. В результате получим . Так как - корень многочлена, то . Отсюда . Подставим теперь в многочлен . Ранее было показано, что если в выражениях для суммы, разности, произведения комплексных чисел заменить каждое комплексное число сопряженным, то и результаты указанных операций заменятся сопряженными числами (см. лемму). Поэтому в результате подстановки в получим число, сопряженное с числом . То есть . Так как , то , то есть значение также является корнем многочлена .

Таким образом, в разложении многочлена с действительными коэффициентами комплексные корни входят попарно сопряженными. Перемножив линейные множители этого разложения, соответствующие паре комплексно-сопряженных корней, получим трехчлен второй степени с действительными коэффициентами:

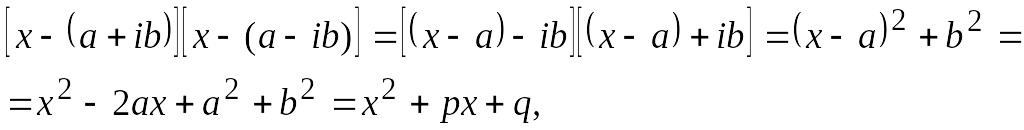где введены обозначения: , - действительные числа.

Если число является корнем кратности k, то сопряженное ему число должно являться корнем той же кратности k. Поэтому наряду с линейными множителями в разложение многочлена входят столько же линейных множителей вида . После перемножения они дадут трехчлен второй степени с действительными коэффициентами в степени k.

Таким образом, многочлен с действительными коэффициентами разлагается на множители с действительными коэффициентами первой и второй степени соответствующей кратности. То есть

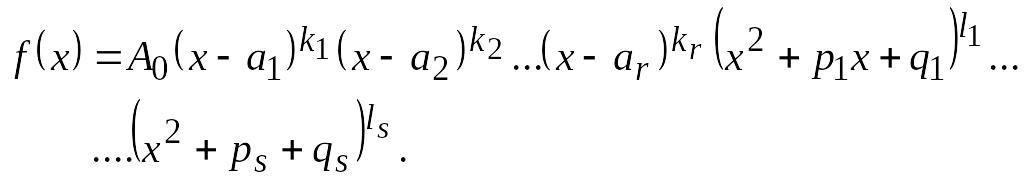При этом