Таким образом, при любом х имеет место разложение
.
Р а з л о ж е н и е
ф у н к ц и и
.
Имеем:
откуда, полагая
х =
0, получаем:
,
Составим по формуле (4.13) для функции
ряд Маклорена:
Легко проверить, что полученный ряд сходится абсолютно на всей числовой прямой. Исследуем остаточный член
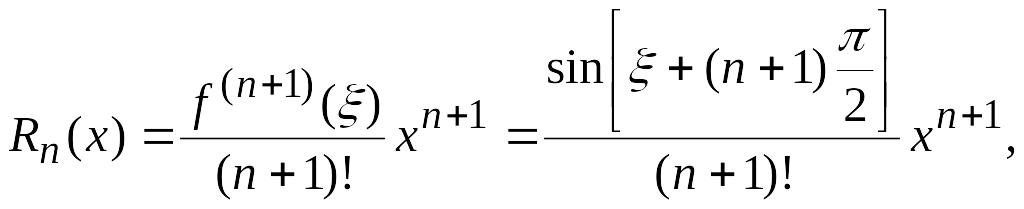
где
.
Так как
,
то
.
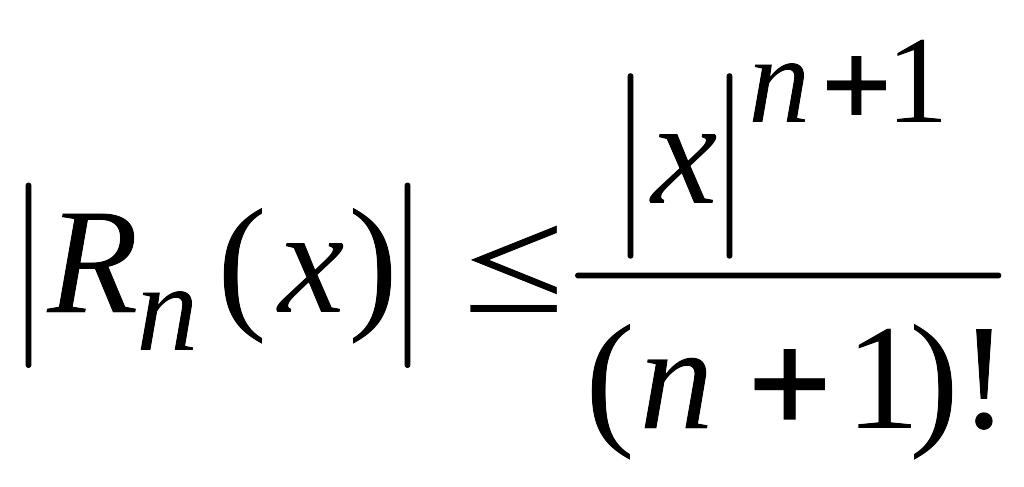В силу (4.16)
.
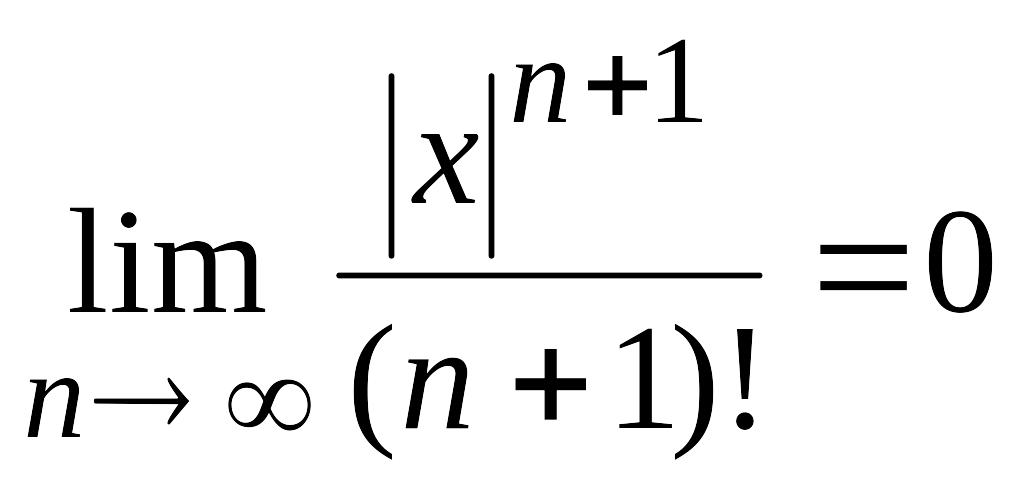Следовательно,
при любом х.
А это означает, что функция
является суммой построенного ряда, т.
е. имеет место разложение
.
Р а з л о ж е н и е
ф у н к ц и и
.
Аналогично предыдущему, можно получить
разложение функции
в ряд Маклорена, справедливое при любом
х.
Однако еще проще разложение
получается почленным дифференци-рованием
ряда для
:
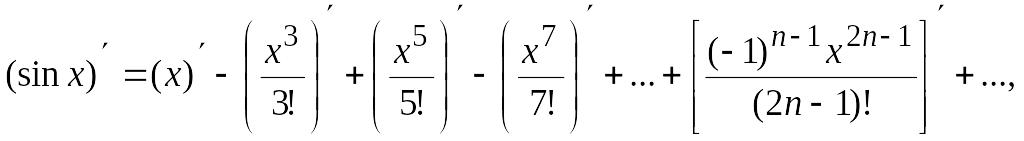откуда
.
Кроме
рассмотренных функций
,
,
в ряд Маклорена могут быть разложены и
многие другие функции. Вместо ряда
Маклорена можно было бы рассмотреть
более общий ряд Тейлора по степеням
,
где
,
т.е. ряд вида
Все изложенное полностью переносится и на эти ряды.
При разложении
функции
в ряд Маклорена было использовано
свойство почленной дифференцируемости
степенных рядов. Аналогично можно
использовать и другое свойство степенных
рядов – их почленную интегрируемость.
В качестве примера разложим с помощью
почленного интегрирования в степенные
ряды функции
и
.
Рассмотрим ряд
Данный ряд является геометрической
прогрессией, первый член которой равен
единице, а знаменатель
.
Как известно, при
данный ряд сходится и его сумма равна
.
Следовательно,
. (4.17)
Равенство (4.17)
является разложением функции
в степенной ряд.
Подставляя в
равенство (4.17)
вместо х, получаем равенство
справедливое при
Проинтегрируем этот степенной ряд
почленно в пределах от 0 до х (
).
Имеем
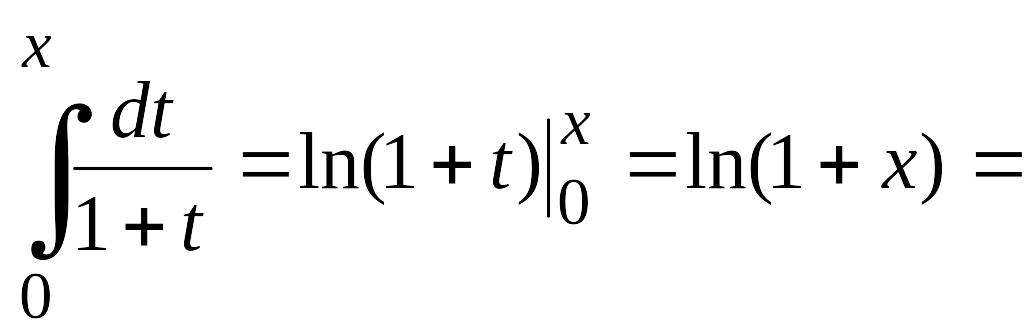
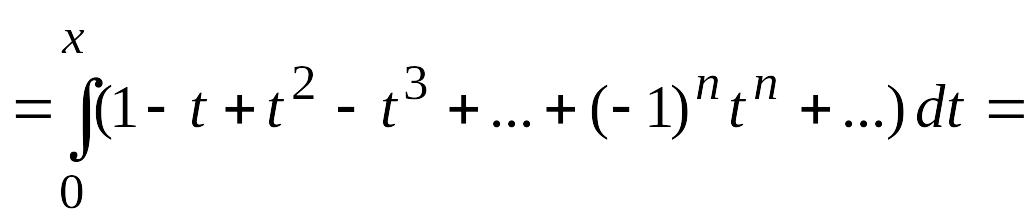
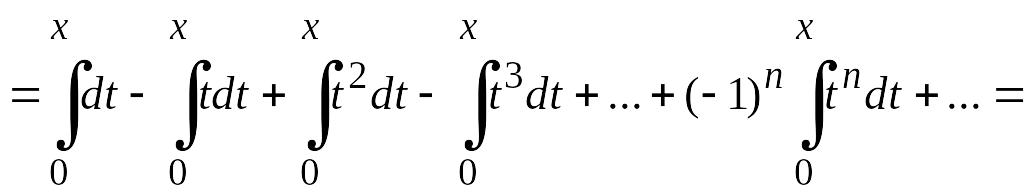
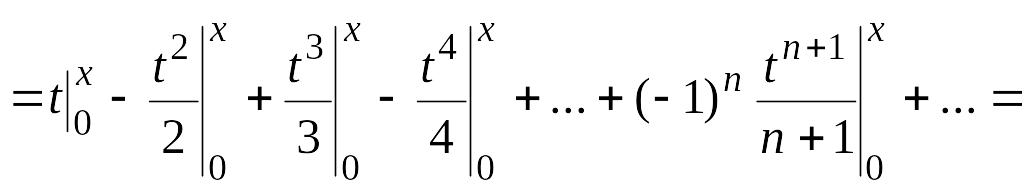
Отсюда
. (4.18)
Равенство (4.18)
является разложением функции
в степенной ряд. Оно справедливо при
.
Можно доказать, что это равенство верно
и для
.
Действительно, при
левая часть (4.18) равна
,
а правая часть – сходящийся по признаку
Лейбница числовой ряд
.
(4.19)
Остается проверить справедливость равенства
(4.20)
Для этого проинтегрируем от 0 до 1 выражение
,
полученное в
результате деления единицы на
.
Имеем
,
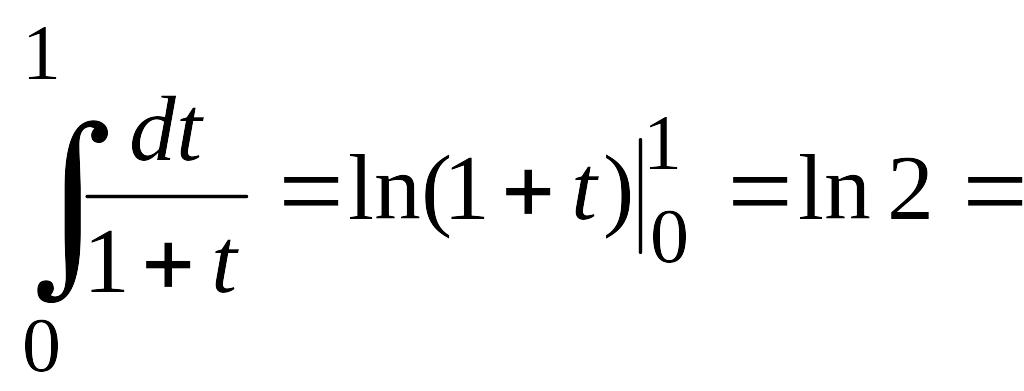
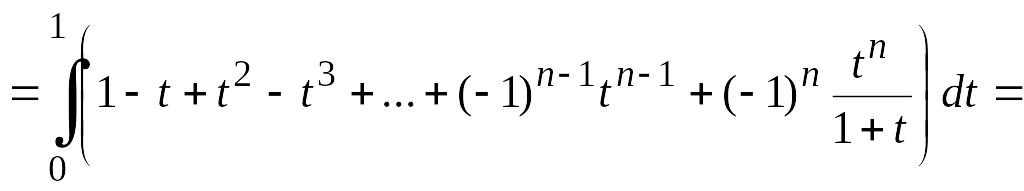
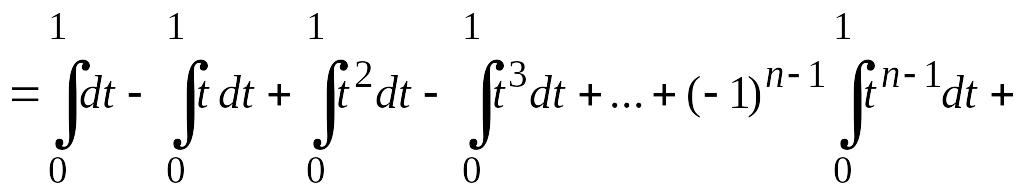
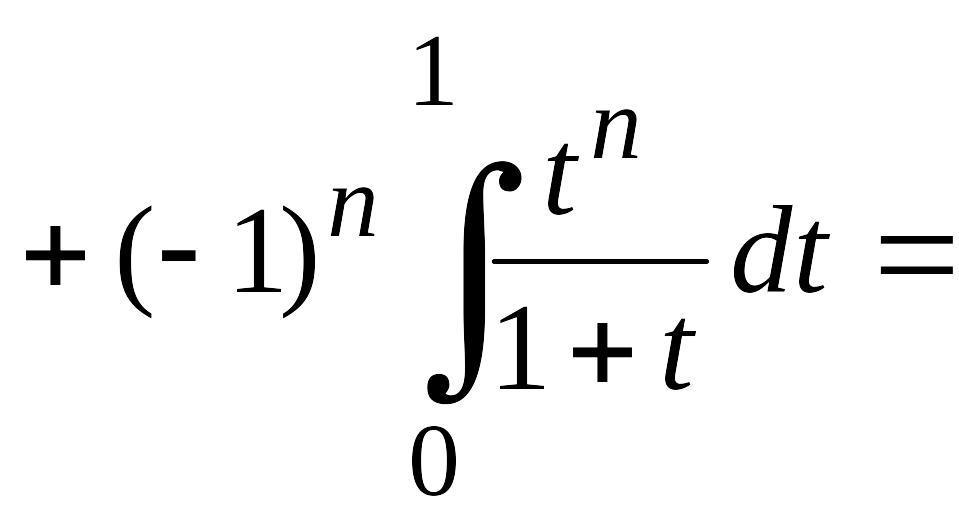
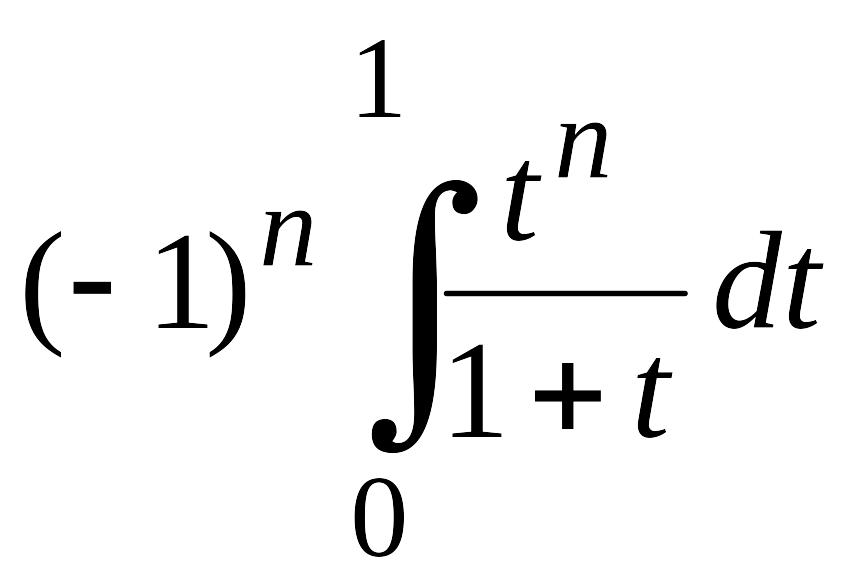т. е.
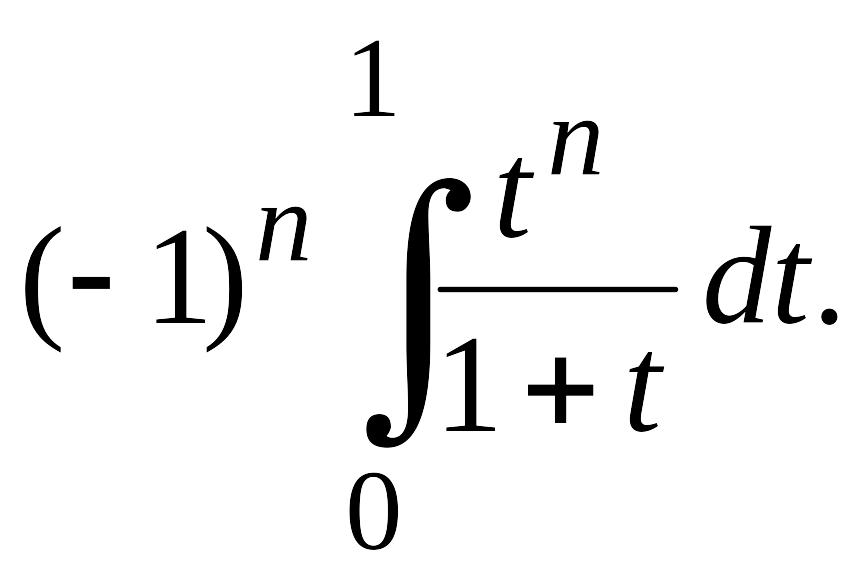(4.21)
В этом равенстве
сумма первых п слагаемых является
частичной суммой
ряда (4.19). Запишем (4.21) в виде
=
(4.22)
Так как
при
то
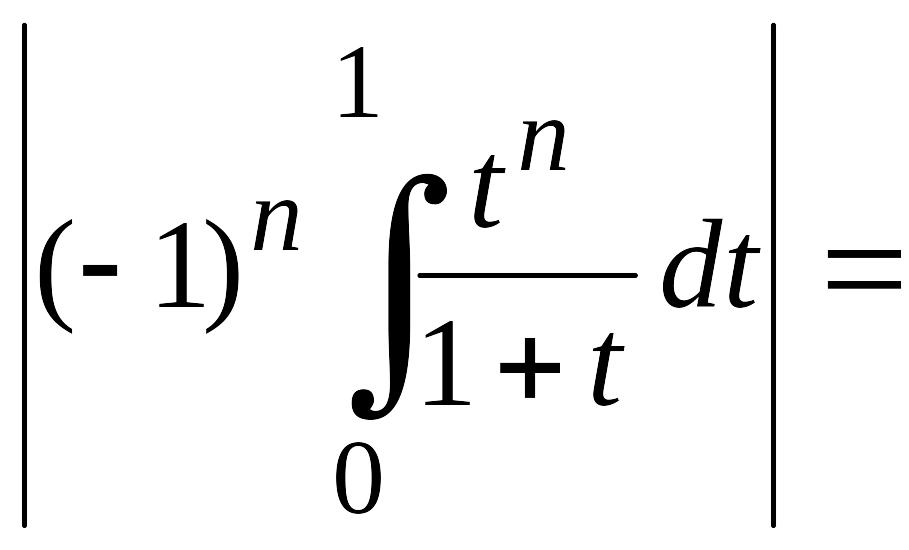
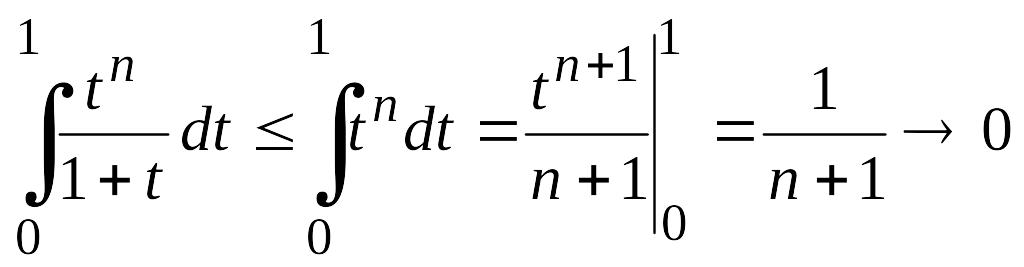
при . Отсюда заключаем, что интеграл в правой части
(4.22) стремится к нулю при , следовательно,
что
и означает справедливость равенства
(4.20).
Найдем теперь
разложение функции
.
Подставляя в (4.17)
вместо х
и интегрируя по t
от 0 до х,
имеем
. (4.23)
Равенство (4.23) справедливо при . Однако аналогично предыдущему можно показать, что оно верно и для .
В заключение
отметим, что степенные ряды имеют
разнообразные приложения. С их помощью
с любой заданной точностью вычисляют
значения функций (в частности, значения
и е);
находят приближенные значения определенных
интегралов, которые или не выражаются
через элементарные функции, или сложны
для вычислений. Так, например, интеграл
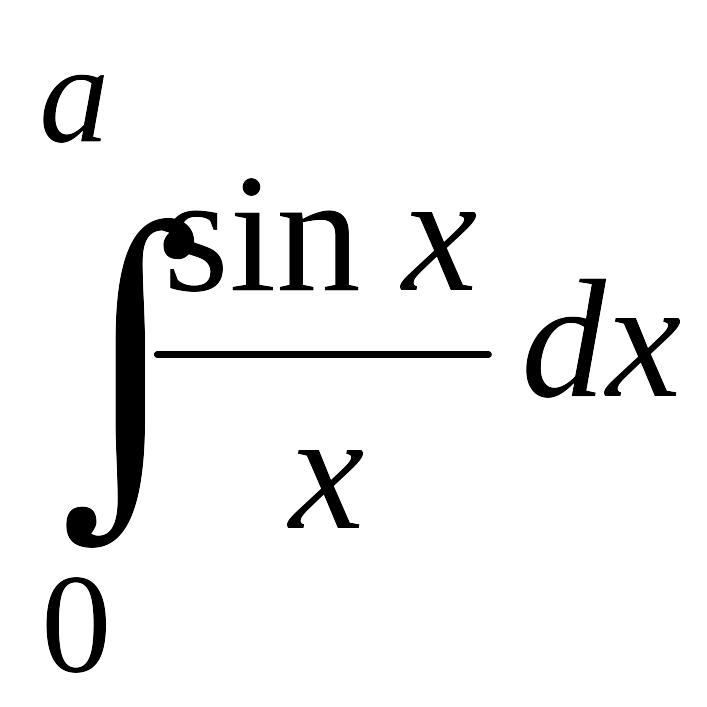не берется в элементарных функциях,
поскольку первообразная функции
не является элементарной. В то же время
эта первообразная легко выражается в
виде степенного ряда. Действительно,
так как
то, умножая этот ряд на
,
получаем
причем последний ряд сходится при любом
х.
Интегрируя его почленно от 0 до а,
имеем
.
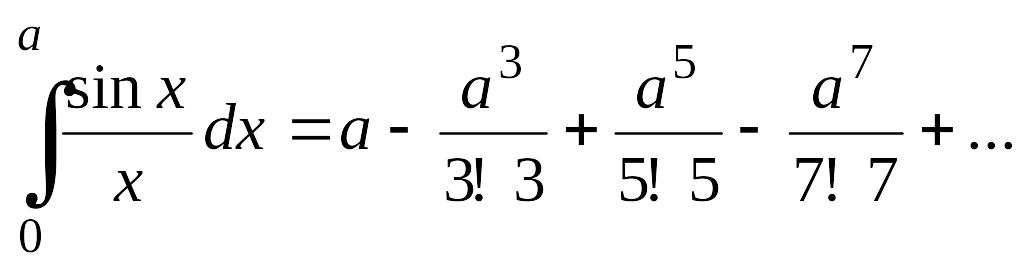С помощью этого равенства можно при любом а с любой степенью точности вычислить данный интеграл.