1.2. Основные действия над комплексными числами

Рассмотрим два комплексных числа и . Суммой двух комплексных чисел и называется комплексное число, определяемое равенством Аналогично, разностью двух комплексных чисел и называется комплексное число, определяемое равенством Произведением двух комплексных чисел и называется комплексное число, которое получается, если мы перемножим и как двучлены по правилам алгебры с учетом того, что

то есть:

Замечение 1. В соответствии с этим правилом произведение сопряженных комплексных чисел и выражается так:

то есть равно квадрату модуля каждого из них.

Деление комплексных чисел определяется как действие, обратное умножению. Практически оно выполняется так: чтобы разделить на , умножим делимое и делитель на комплексное число, сопряженное делителю, то есть на . Тогда делителем будет действительное число. Разделив на него действительную и мнимую части делимого, получим частное

,

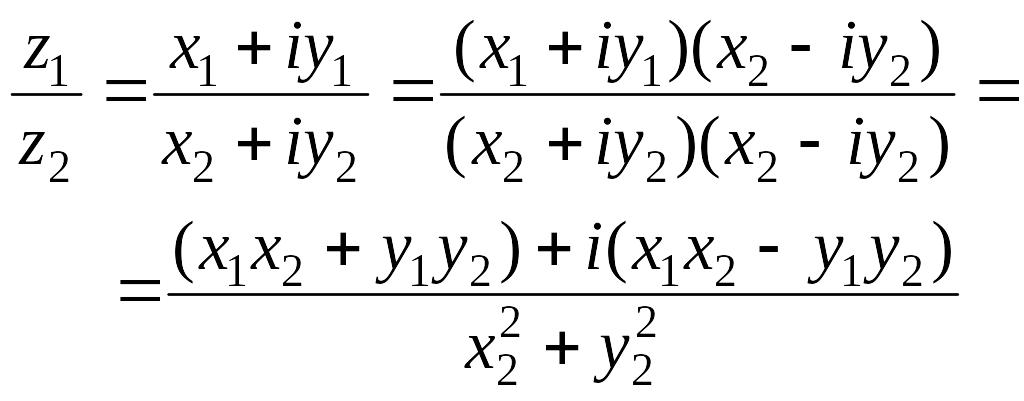то есть

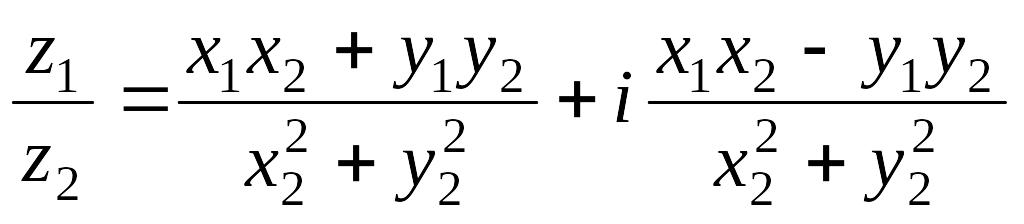
Замечание 2. Если в выражениях для суммы, разности, произведения и частного комплексных чисел заменить каждое комплексное число сопряженным, то и результат указанных операций заменится сопряженным числом. То есть:

_.

Доказательство проведем для соотношения:

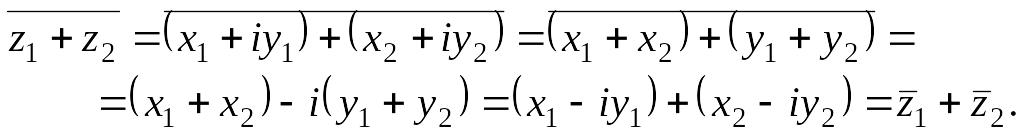
Остальные соотношения доказываются аналогично. Отсюда вытекает следующая лемма:

Лемма: Если в многочлен с действительными коэффициентами подставить , а затем сопряженное число , то и результаты этих подстановок будут взаимно-сопряженными. То есть

Выполнение операций умножения и деления двух комплексных чисел существенно упрощается, если эти числа заданны в тригонометрической форме. Пусть , . Тогда, выполнив умножение, получим:

_(**)

то есть модуль произведения равен произведению модулей сомножителей, а аргумент равен сумме аргументов сомножителей.

Для деления имеем:

.

Это равенство легко проверяется умножение делителя на частное. То есть модуль частного равен частному модулей делимого и делителя, а аргумент равен разности аргументов делимого и делителя.

1.3. Возведение в степень и извлечение корня из комплексного числа

Из формулы (**) следует, что если n - целое положительное число, то

Эта формула называется формулой Муавра. Она показывает, что при возведении комплексного числа в целую положительную степень модуль возводится в эту степень, а аргумент умножается на показатель степени.

Пример. Вычислить .

Решение. Представим комплексное число в тригонометрической форме: . Здесь . Применяя формулу возведения в степень, получим:

Рассмотрим задачу о вычислении корня n-ой степени из комплексного числа . По определению, комплексное число является корнем n-ой степени из z, то есть , если его n-я степень равняется подкоренному числу:

Так как у равных комплексных чисел модули должны быть равны, а аргументы могут отличаться на число, кратное , то получаем: . Отсюда , где k-любое целое число, -арифметическое значение корня (действительное, положительное). Следовательно,

Придавая k значениям получим n различных значений корня. Для других значений k аргументы корней будут отличаться от уже полученных на число, кратное и, следовательно, получатся значения корня, совпадающие с уже рассмотренными.

Т. е., корень n-ой степени из комплексного числа имеет n различных значений. Все n значений корней имеют один и тот же модуль , а аргументы отличаются на одну и ту же величину . Следовательно, на комплексной плоскости Z точки, соответствующие значениям являются вершинами правильного n - угольника, вписанного в окружность радиуса с центром в начале координат.

Пример. Найти все значения .

Решение. Для Т. е.

,

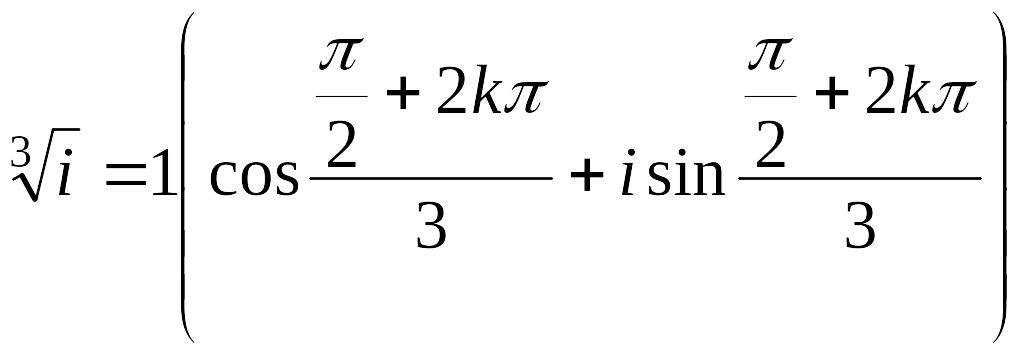(Рис. 3)