4.6. Ряды Фурье

1. Тригонометрический ряд и его основные свойства. Определение. Ряд вида

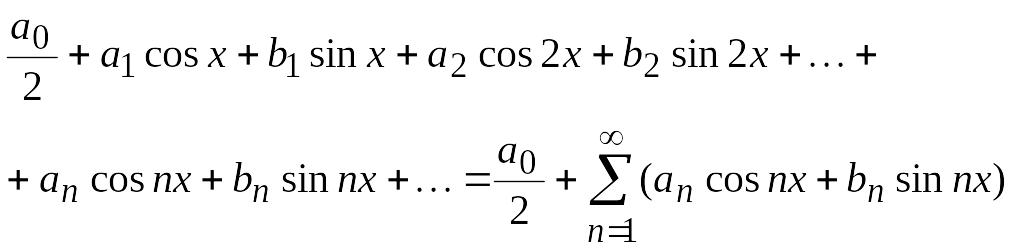(4.24)

называется тригонометрическим рядом, а числа коэффициентами тригонометри-ческого ряда.

В отличие от степенного ряда, рассмотренного ранее, в тригоно­метрическом ряде вместо простейших функций взяты тригонометрические функции

(4.25)

которые также хорошо изучены.

Прежде всего отметим, что все функции системы (4.25) являются периодическими с периодом . В самом деле, постоянная имеет любой период, а период функций sin nx и cos nx (n = l, 2, ...) равен и, следовательно, каждый член тригонометрического ря­да (4.24) является периодической функцией с периодом . По­этому и любая частичная сумма ряда (4.24) -периодична (если все члены ряда не меняются от замены х на , то и сумма его не изменяется от этой замены). Отсюда следует, что если ряд (4.24) сходится на отрезке то он сходится на всей число­вой прямой и его сумма, будучи пределом последовательности пе­риодических частичных сумм, является периодической функцией с периодом . Поэтому тригонометрические ряды особенно удобны при изучении периодических функций, описывающих различные периодические процессы, которые имеют место в природе и технике. Примерами периодических процессов служат колебательные и вра­щательные движения различных деталей машин и приборов, перио­дическое движение небесных тел и элементарных частиц, акусти­ческие и электромагнитные колебания и др.

Другим важным свойством функций системы (4.25) является их ортогональность на отрезке в следующем смысле: интеграл по отрезку от произведения любых двух различных функ­ций этой системы равен нулю, а интеграл по отрезку от квадрата любой функции этой системы отличен от нуля. Действительно,

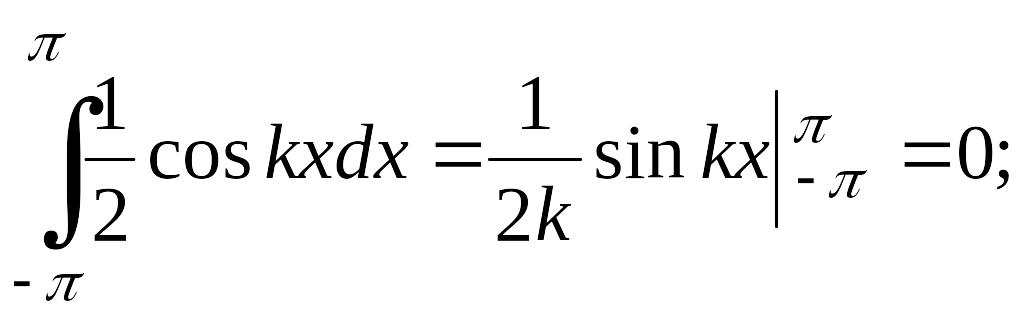
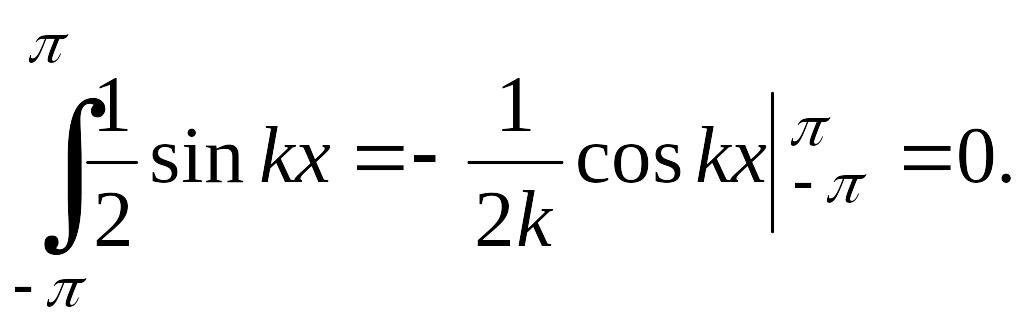(4.26)

Далее,

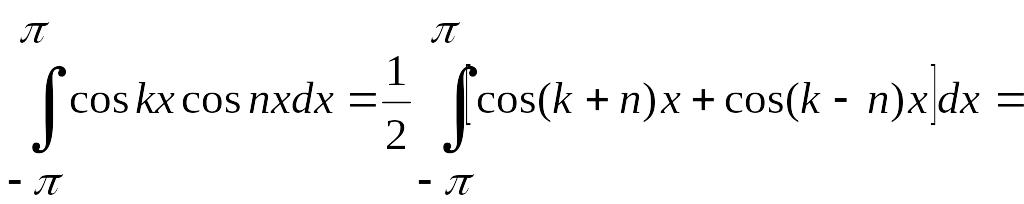
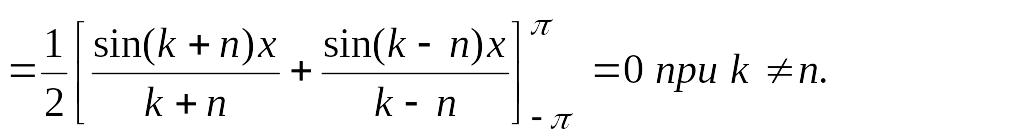(4.27)

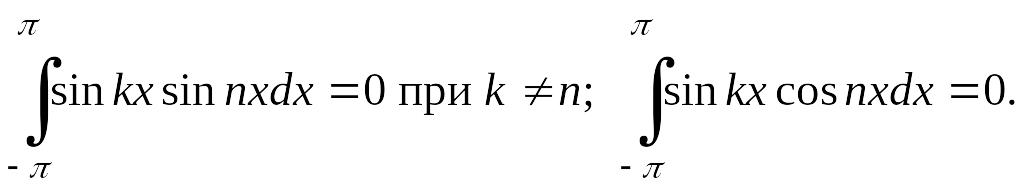(4.28)

Наконец,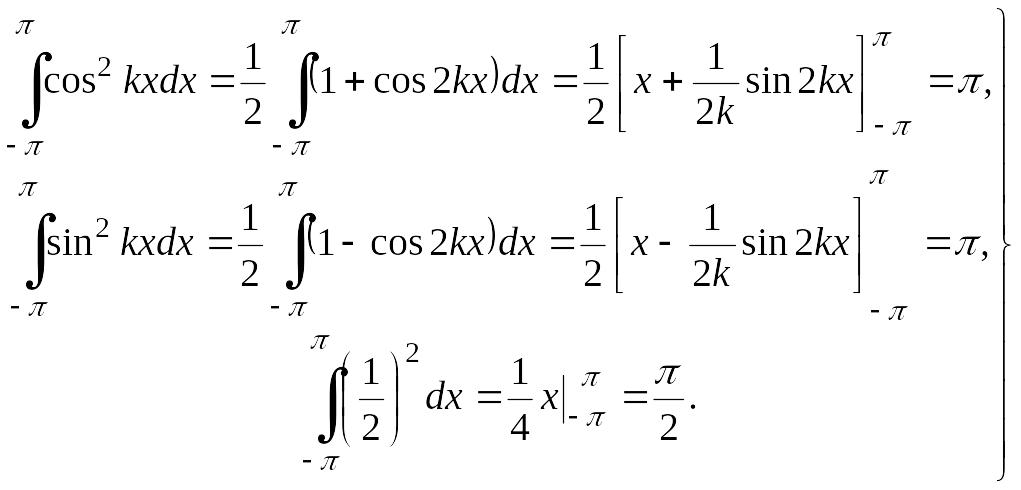 (4.29)

что и требовалось показать.

2. Ряд Фурье. Аналогично степенному ряду, для тригонометри­ческого ряда имеет место следующая теорема.

Теорема 19. Если функция определена и интегри­руема на отрезке , разлагается в тригонометрический ряд

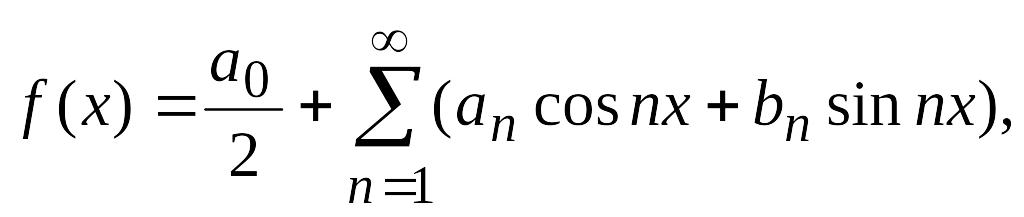(4.30)

который можно интегрировать почленно, то это разложение единственно.

Д о к а з а т е л ь с т в о. Интегрируя (4.30), получаем

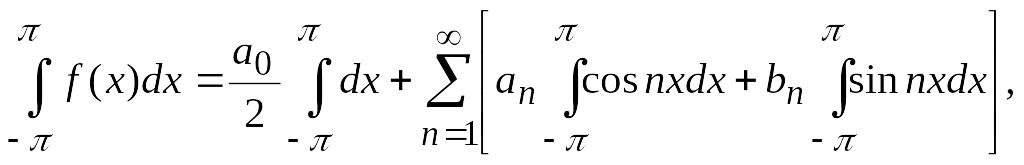
откуда, учитывая (4.26), находим 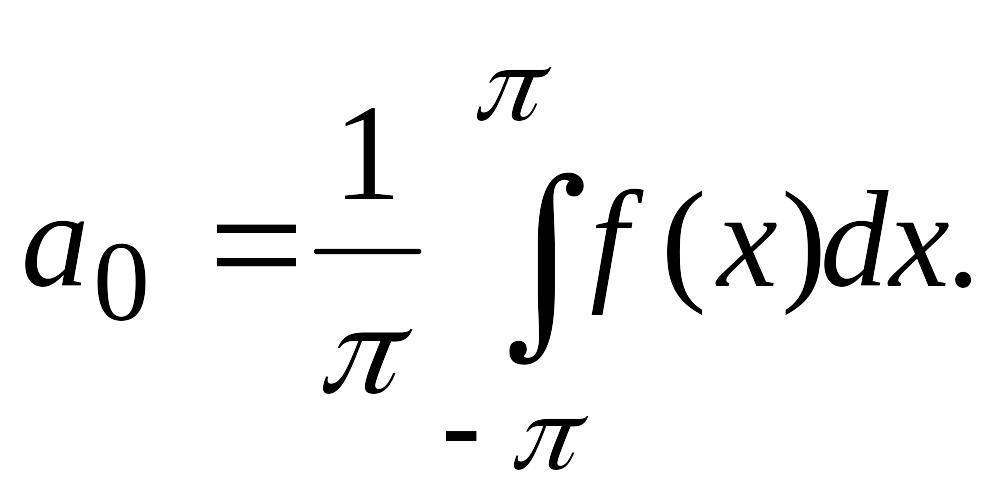(4.31)

Для определения коэффициента при (k – натуральное число) умножим равенство (4.30) на и проинтегрируем по х от  до . Тогда на основании формул (4.26)  (4.29) получаем

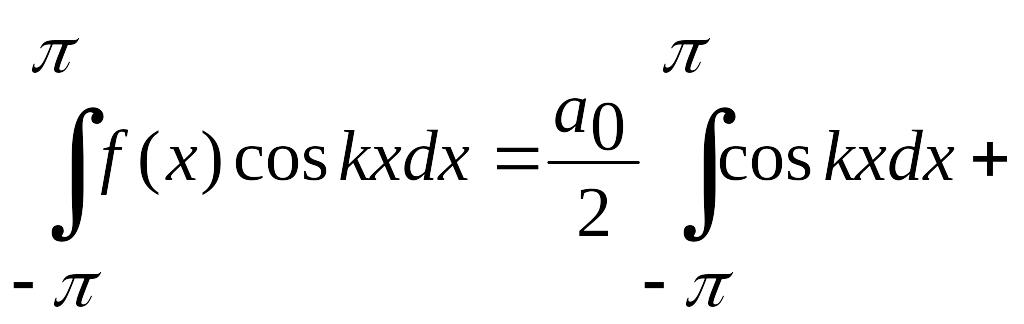
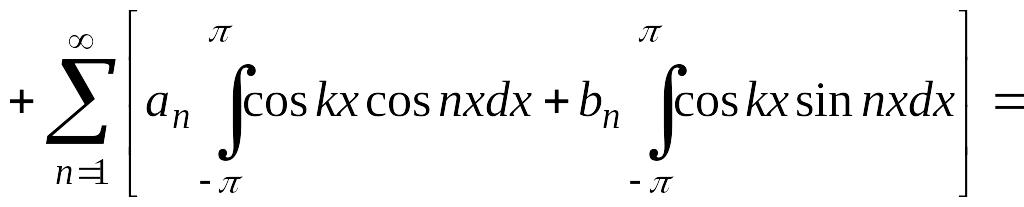
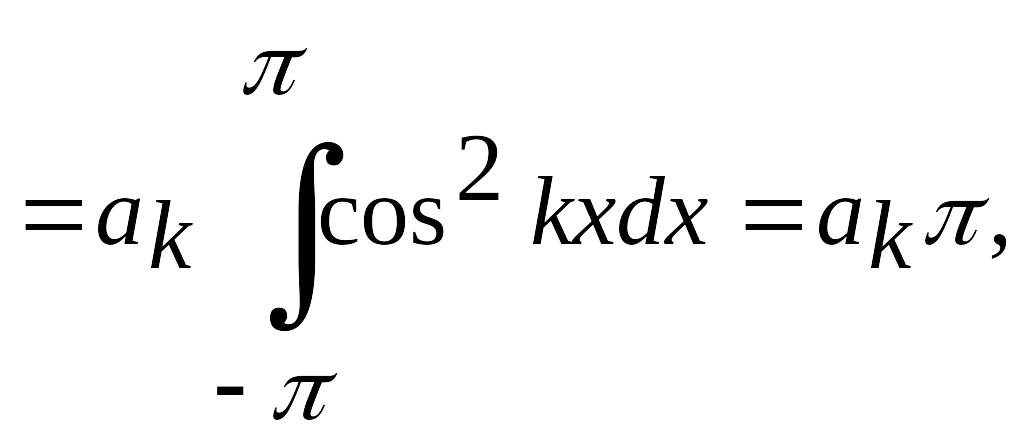
откуда

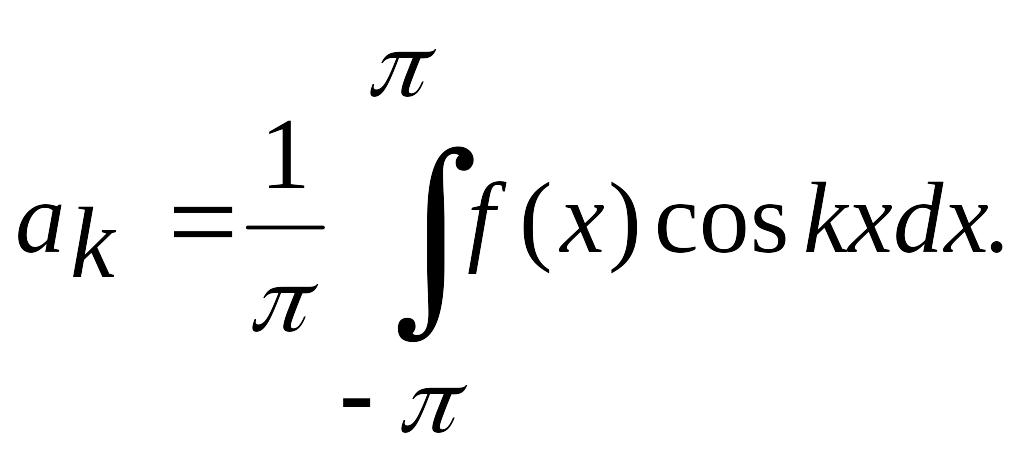. (4.32)

Аналогично, умножая равенство (4.30) на и интегрируя в пределах от до , на основании тех же формул получаем 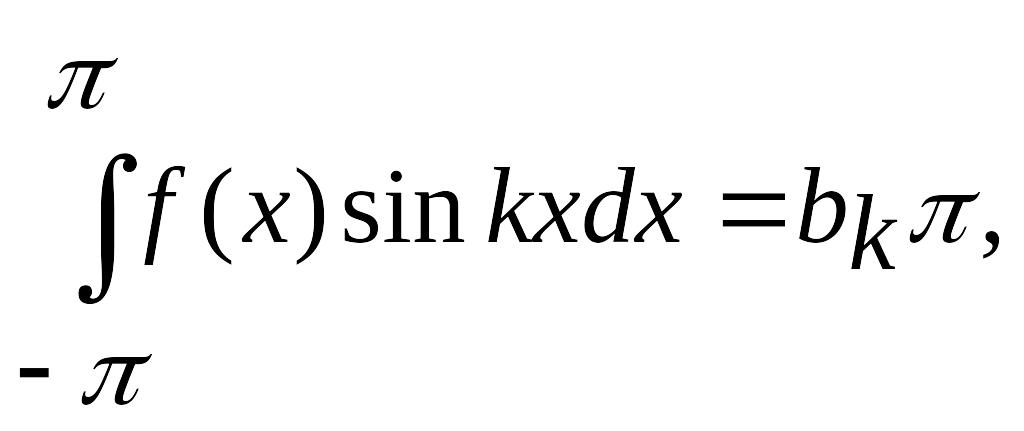откуда находим

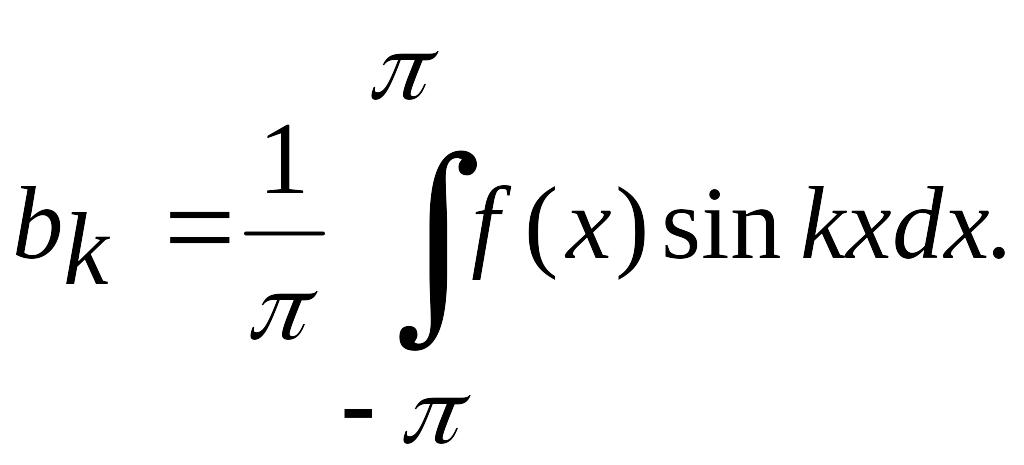. (4.33)

Таким образом, коэффициенты и ряда (4.30) определяются единственным образом формулами (4.31)  (4.33), что и доказывает теорему, которая дает основание ввести следующее определение.

Определение. Пусть  функция, определенная и интегри­руемая на отрезке Тогда числа , найденные по формулам (4.31)  (4.33), называются коэффици-ентами Фурье, а ряд 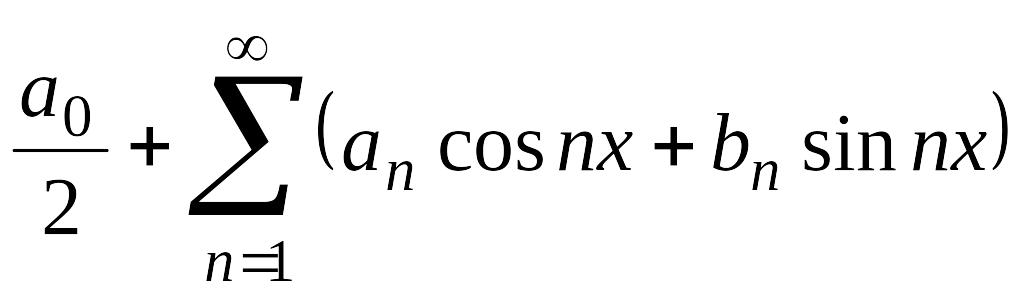с этими коэффициентами называется рядом Фурье функции .

3. Сходимость ряда Фурье. Введем понятие периодического продолжения функции , заданной на отрезке . Будем говорить, что функция F(x), определенная на всей число­вой прямой и периодическая с периодом , является периодиче­ским продолжением функции , если на отрезке

Очевидно, что если на отрезке ряд Фурье сходится к функции , то он сходится на всей числовой прямой к ее

периоди­ческому продолжению.

Установим, при каких условиях ряд Фурье функции схо­дится к этой функции. Ответ на поставленный вопрос дает следующая теорема.

Теорема 20. Пусть функция и ее производная  непрерывные функции на отрезке или же имеют на нем ко­нечное число точек разрыва 1-го рода, Тогда ряд Фурье функции сходится на всей числовой прямой, причем в каждой точке , в которой непрерывна, сумма ряда равна , а в каждой точке разрыва функции сумма ряда равна где и На концах отрезка сумма ряда равна . В любой точке сумма ряда Фурье равна F(x), если х – точка непрерывности F(x) и равна если х – точка разрыва F(x), где F(x) – периодическое продолжение .

4. Ряды Фурье для четных и нечетных функций. Пусть функция f(x) определена на отрезке и является четной, т.е. . Тогда ее коэффициенты Фурье равны нулю. Действитель­но,

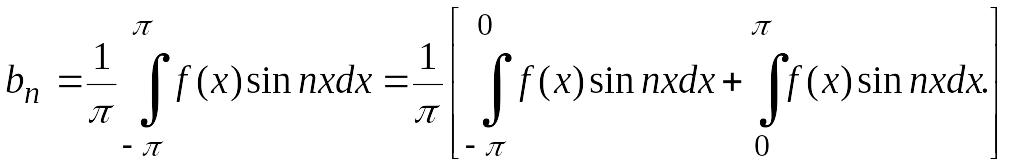
В первом интеграле в квадратных скобках сделаем замену перемен­ной. Положим x = t. Тогда dx = dt; если , то

; если то Принимая во внимание, что

функция четная, а функция sin х  нечетная, получаем

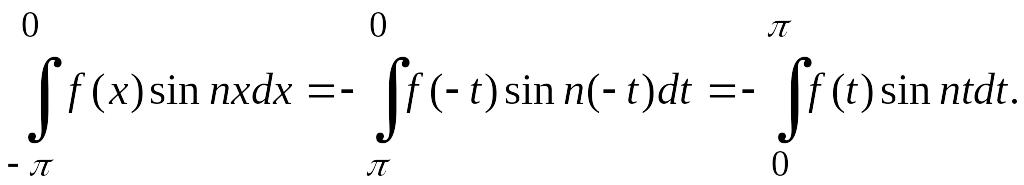
Следовательно,

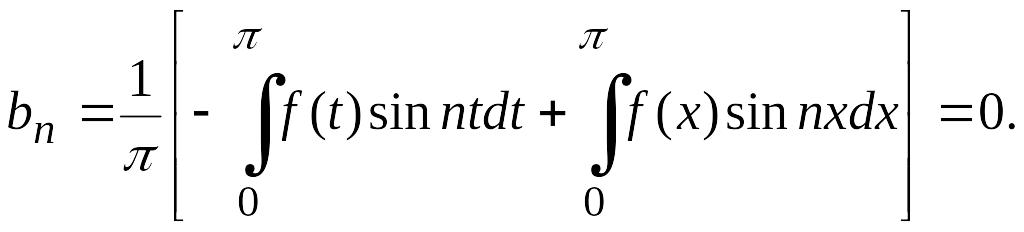
Аналогично, учитывая, что функции и четные, можно получить следующие выражения для коэффициентов :

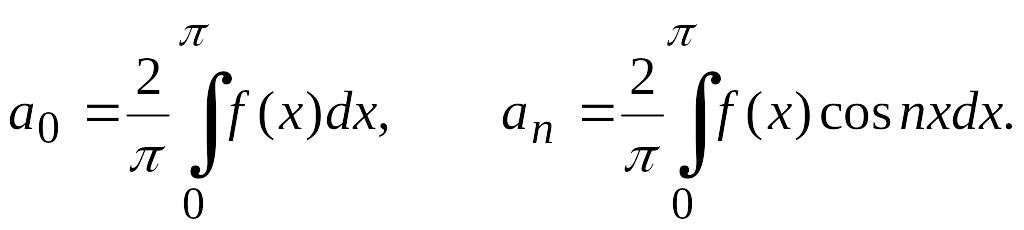(4.34)

Пусть теперь функция , определенная на отрезке , нечетная, т.е. . Тогда, используя рассуждения, аналогичные приведенным выше, можно показать, что коэффициен­ты Фурье равны нулю, а коэффициенты определяются выражениями

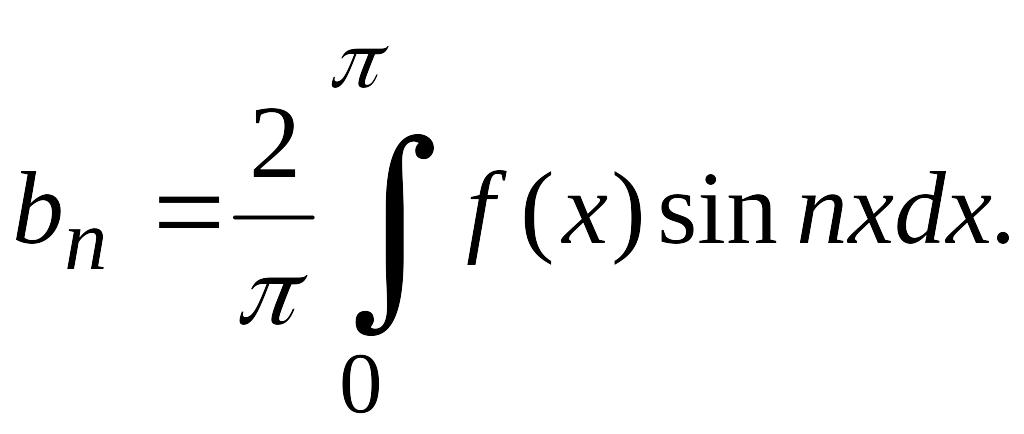(4.35)

Таким образом, если функция четная, то ряд Фурье содер­жит только косинусы и только синусы, если функция нечетная. Формулы (4.34) и (4.35) позволяют упростить вычисление коэффициен­тов Фурье, когда заданная функция является четной или нечетной.

Пример 1. Рассмотрим функцию = x. Эта функция удовле­творяет условиям теоремы 19 и, следовательно, может быть разложена в ряд Фурье. Так как она нечетная, то ее коэффициенты находятся по формуле (4.35). Имеем

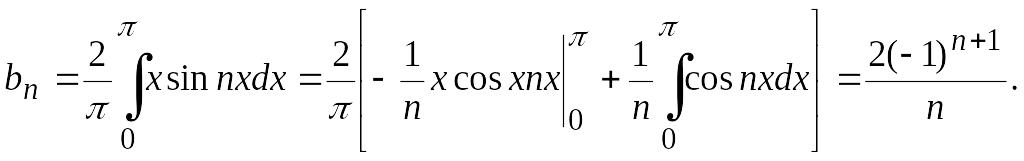Таким образом, получаем ряд Фурье данной функции

Это равенство справедливо для любого . В точках сумма ряда Фурье по теореме 19 не совпадает со значениями функции а равна

Вне отрезка сумма ряда является периодическим продолже­нием функции =x; ее график изображен на рис. 21, а.

Пример 2. Рассмотрим функцию Эта функция удов­летворяет условиям теоремы 19 и, следовательно, может быть разложена в ряд Фурье. Так как она чётная, то ее коэффициенты Фурье а находятся по формулам (4.34). Имеем

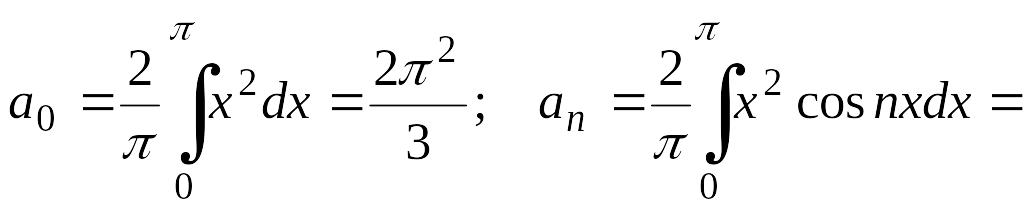
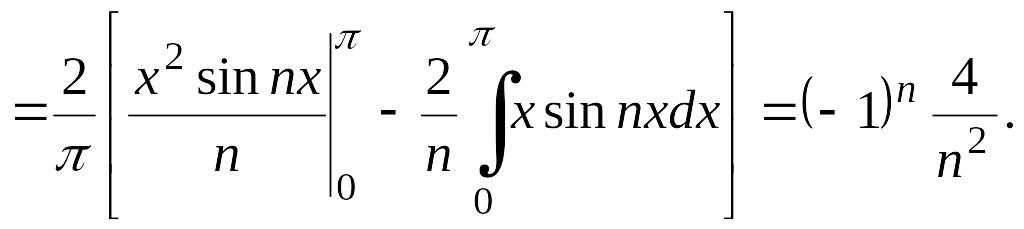
Значит, ряд Фурье данной функции имеет вид

Это равенство справедливо для любого , так как в точках сумма ряда в данном случае совпадает со значениями функции поскольку

График функции и суммы данного ряда Фурье изображены на рис. 21, б.

Рис. 21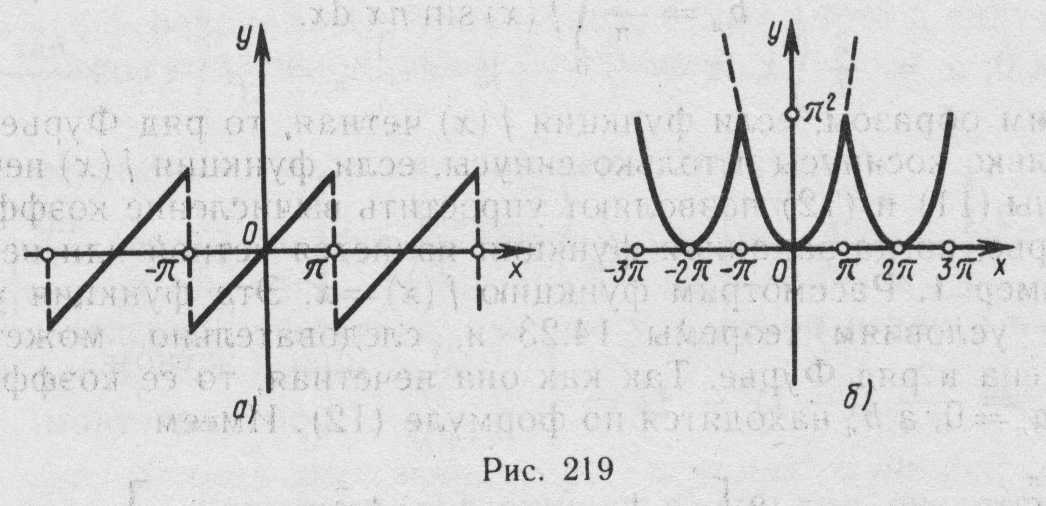

5. Ряд Фурье с периодом 2l. Пусть, функция определена на отрезке произвольное положительное число) и удовлетворяет на этом отрезке условиям теоремы 19. Разложим ее в ряд Фурье. Введем новую переменную по формуле и рассмотрим функцию . Очевидно, функция определена на отрезке и удовлетворяет на нем условиям теорема 19. Разложим функцию на отрезке в ряд Фурье

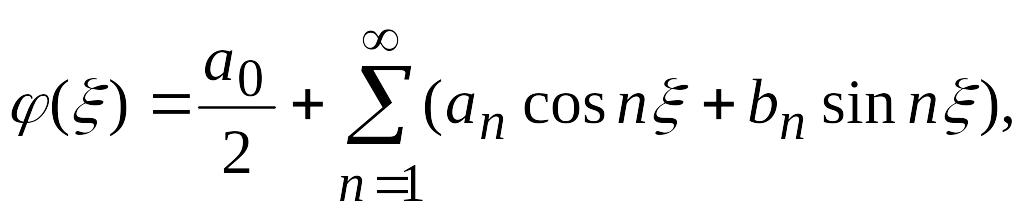(4.36)

где

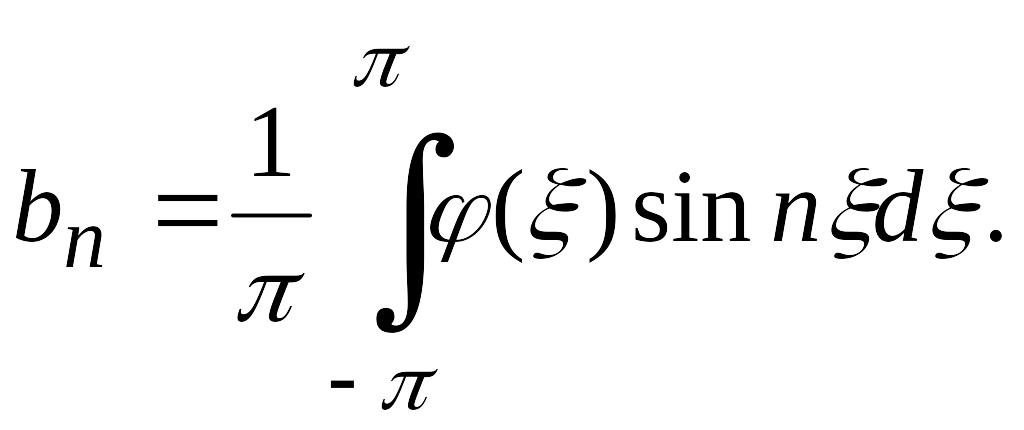
Вернемся теперь к старой переменной х: , Тогда формула (4.36) принимает вид

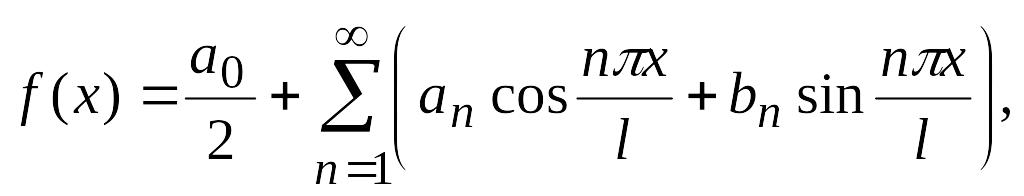(4.37)

где

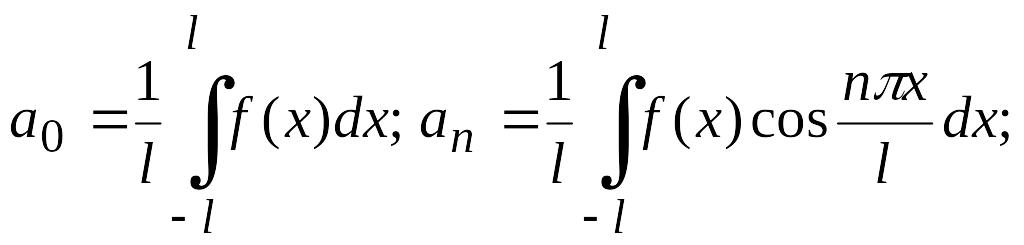
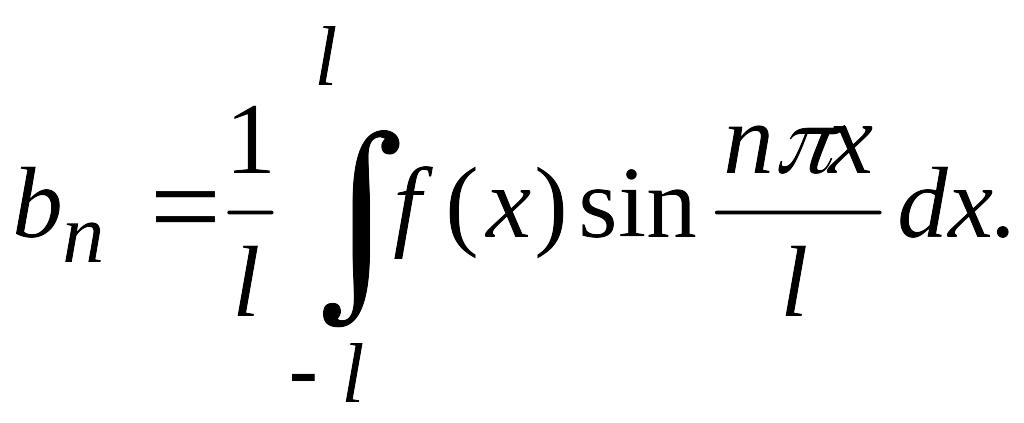
Формула (4.37) и есть ряд Фурье с периодом 2l.

Пример 3. Разложить в ряд Фурье с периодом 2l функцию , которая на отрезке задается формулой

Решение. Так как функция четная, то

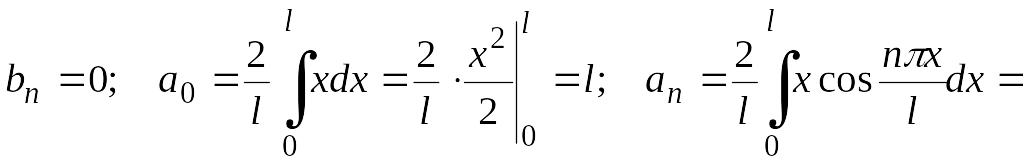
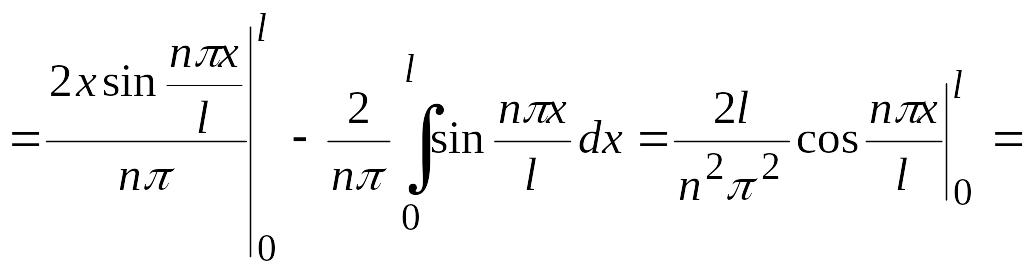
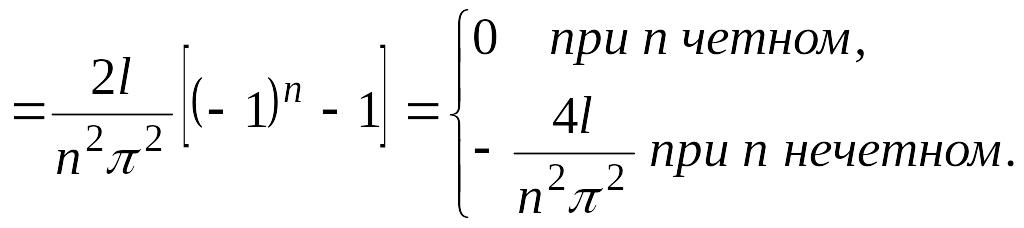
Следовательно, ряд Фурье функции имеет вид

Ф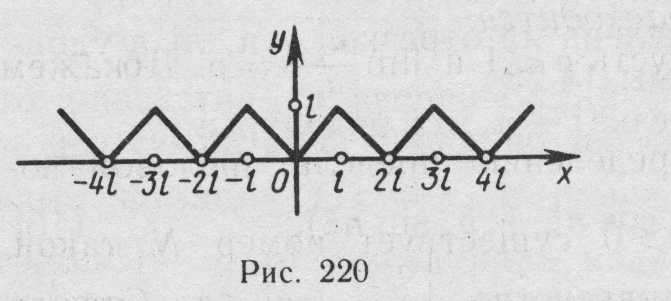 ункция удовлетворяет условиям теоремы 19 и полученное равенство справедливо для лю­бого , а это значит, что ряд сходится на всей число­вой прямой и его суммой явля­ется функция, график которой изображен на рис. 22.

О

Рис. 22

тметим, что ряды Фурье имеют широкое применение как в теоретических исследованиях, так и в практических задачах.