
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко математический анализ
- •Часть 2
- •Учебное пособие
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко
- •Часть 2
- •Воронеж 2013
- •Введение
- •1. Комплексные числа и действия над ними
- •1.1. Комплексные числа. Основные определения
- •1.2. Основные действия над комплексными числами
- •1.3. Возведение в степень и извлечение корня из комплексного числа
- •1.4. Применение формул Эйлера и Муавра
- •1.5. Многочлены в комплексной области
- •Задачи к п. 1
- •Ответы к п.1
- •Неопределенный интеграл
- •2.1. Первообразная и неопределенный интеграл
- •2. Неопределенный интеграл.
- •2.2. Основные свойства неопределенного интеграла
- •2.3. Таблица основных интегралов
- •2.4. Основные методы интегрирования
- •Интегрирование рациональных функций
- •2.6. Интегрирование иррациональных и трансцендентных функций
- •Задачи к п. 2
- •Ответы к п. 2
- •Индивидуальные задания
- •3. Определенный интеграл
- •3.1. Определение определенного интеграла
- •Интегрируемость непрерывных и некоторых разрывных функций Теорема 1. Если функция непрерывна на отрезке то она интегрируема на нем.
- •3.3. Основные свойства определенного интеграла
- •Оценки интегралов. Формула среднего значения
- •2. Формула среднего значения.
- •Интеграл с переменным верхним пределом
- •3.6. Формула Ньютона-Лейбница
- •3.7. Замена переменной в определенном интеграле
- •Пример 1. Вычислить
- •Формула интегрирования по частям в определенном интеграле
- •Некоторые физические и геометрические приложения определенного интеграла
- •3.10. Несобственные интегралы
- •1. Несобственные интегралы с бесконечными пределами интегрирования.
- •2. Несобственные интегралы от неограниченных функций.
- •Задачи к п. 3
- •Ответы к п. 3
- •3.11. Индивидуальные задания
- •Задача 4.
- •Задача 5.
- •Задача 6.
- •4. Ряды
- •4.1. Понятие числового ряда
- •Суммы конечного числа членов ряда
- •2. Свойства сходящихся рядов.
- •Ряды с неотрицательными членами
- •4.3. Знакочередующиеся ряды
- •4.4. Абсолютная и условная сходимость рядов
- •Возьмем какой-нибудь знакопеременный ряд
- •4.5. Степенные ряды
- •Таким образом, при любом х имеет место разложение
- •4.6. Ряды Фурье
- •Задачи к п. 2
- •Ответы к п. 2
- •Библиографический список
- •8. Краснов м.Л. Функции комплексного переменного. Операционное исчисление. Теория устойчивости / м.Л. Краснов, а.И. Киселев, г.И. Макаренко – м.: Наука, 1981. Оглавление
- •1. Комплексные числа и действия над ними …………….4
- •Неопределенный интеграл ……………………......…...23
- •3. Определенный интеграл.….……………....………........68
- •4. Ряды……..…………................………………...…...…...118
- •Бырдин Аркадий Петрович
- •Часть 2
- •394026 Воронеж, Московский просп., 14
Ряды с неотрицательными членами
Перейдем теперь к рассмотрению некоторых достаточных условий сходимости рядов с неотрицательными членами. Предварительно сформулируем теорему, которая будет использована в последующих рассуждениях.
Теорема 5. Для того чтобы ряд с неотрицательными членами сходился, необходимо и достаточно, чтобы последовательность частичных сумм этого ряда была ограничена.
Достаточные условия сходимости ряда. Установим ряд признаков, позволяющих сделать вывод о сходимости (расходимости) рассматриваемого ряда.
Теорема
6
(признак
сравнения).
Пусть даны два ряда с неотрицательными
членами
и
и для всех n
выполняется неравенство
![]() Тогда из сходимости ряда
следует
сходимость ряда
,
а из расходимости ряда
следует расходимость ряда
.
Тогда из сходимости ряда
следует
сходимость ряда
,
а из расходимости ряда
следует расходимость ряда
.
Пример 1.
Ряд
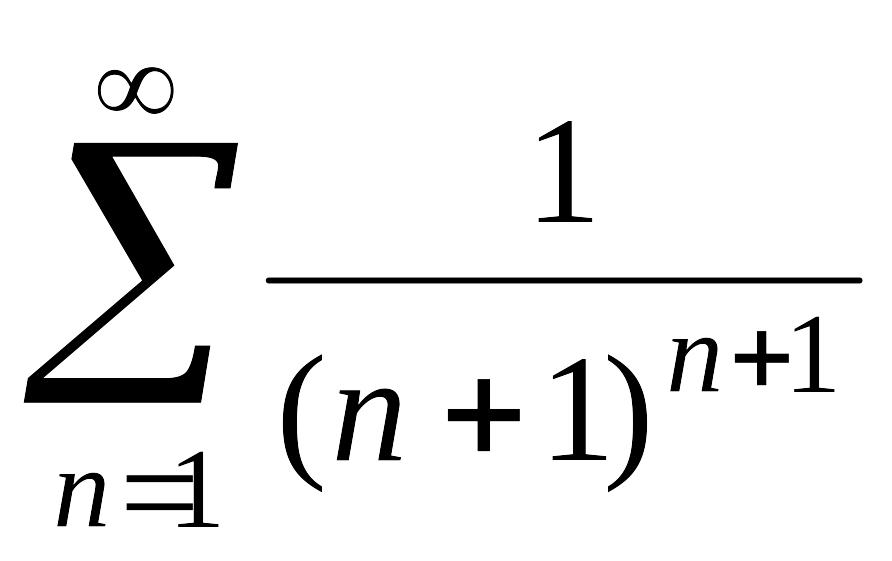 сходится, так как сходится
сходится, так как сходится
ряд из членов
геометрической прогрессии: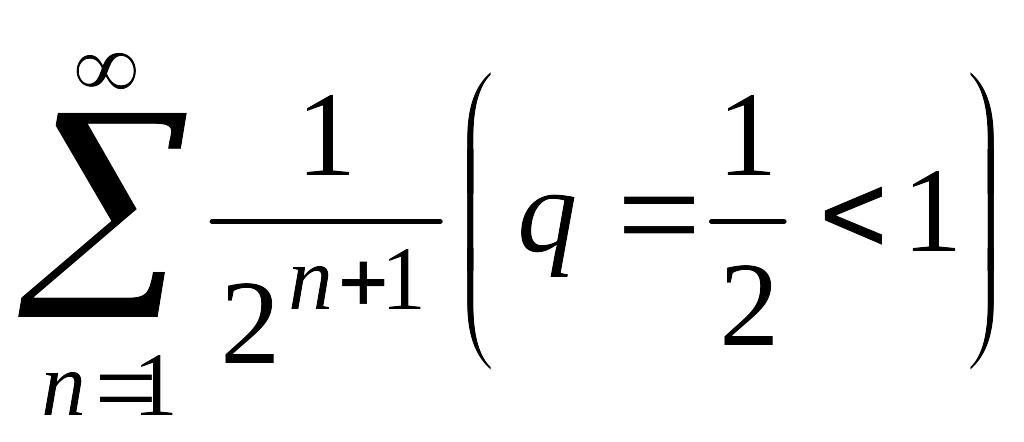 ,
,
а члены данного ряда не больше соответствующих членов ряда
сходящейся
геометрической прогрессии:
![]()
Пример
2. Ряд
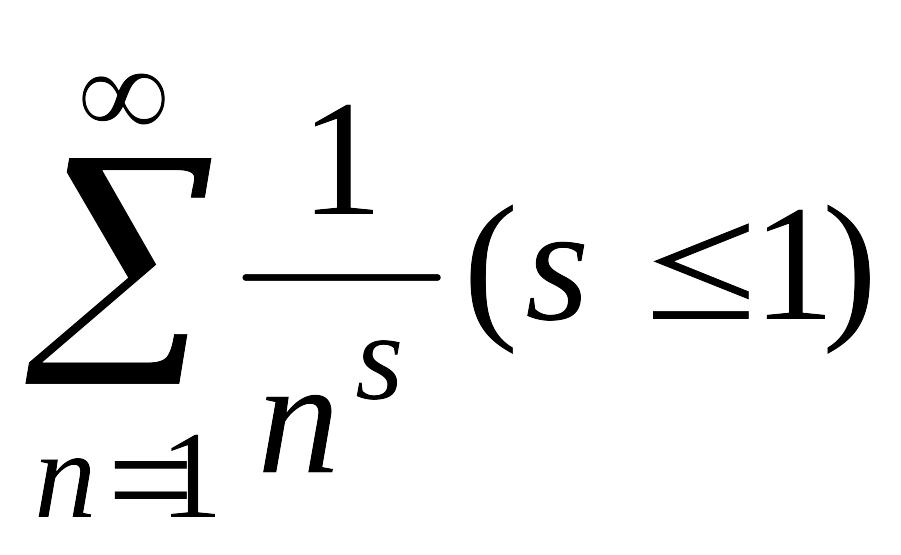 расходится, поскольку его члены не
меньше членов гармонического ряда
расходится, поскольку его члены не
меньше членов гармонического ряда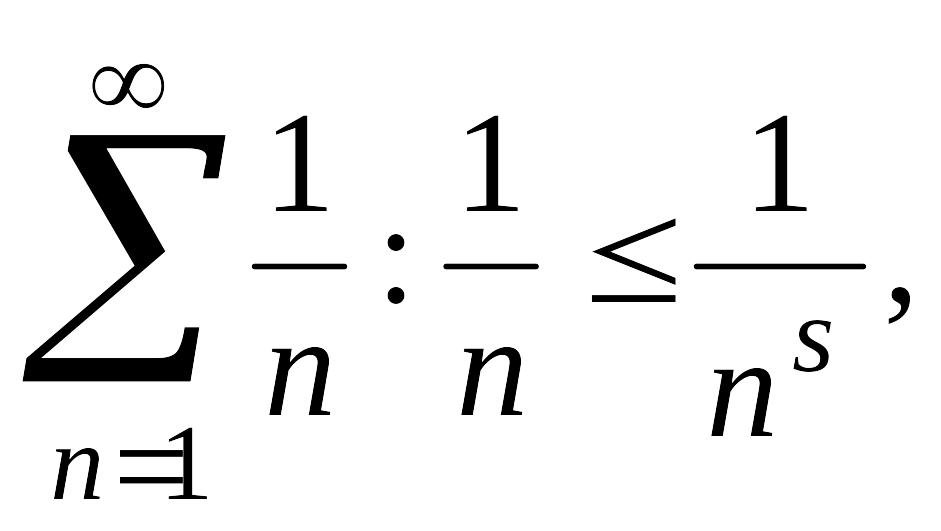 а гармонический ряд расходится.
а гармонический ряд расходится.
Существуют признаки сходимости рядов, позволяющие непосредственно судить о сходимости (или расходимости) данного ряда, не сравнивая его с другим рядом, о котором известно, сходится он или расходится. Рассмотрим два из них.
Теорема
7
(признак
Даламбера).
Пусть дан
ряд
с положительными
членами и существует предел
![]() .
Тогда
а)
при
.
Тогда
а)
при
![]() ряд сходится;
б)
при
ряд сходится;
б)
при
![]() ряд расходится.
ряд расходится.
З а м е ч а н и е.
При
![]() ,
как показывают примеры, ряд
может как сходиться, так и расходиться.
В этом случае необходимо дополнительное
исследование ряда с помощью признака
сравнения или других признаков.
,
как показывают примеры, ряд
может как сходиться, так и расходиться.
В этом случае необходимо дополнительное
исследование ряда с помощью признака
сравнения или других признаков.
Пример 3.
Ряд
![]() сходится, так как
сходится, так как
![]()
Пример
4. Ряд
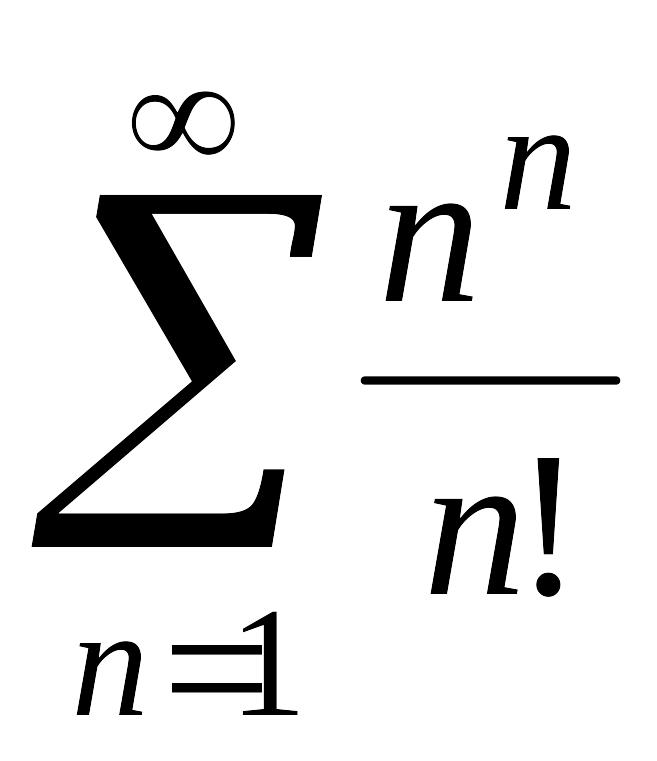 расходится, так как
расходится, так как
![]()
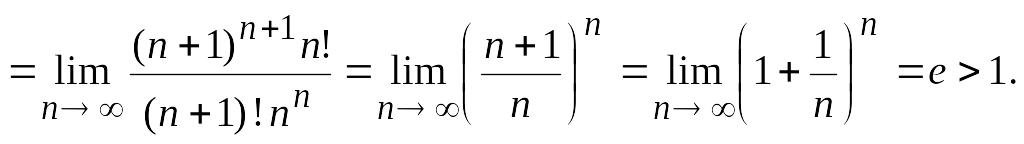
Пример
5.
Рассмотрим ряд
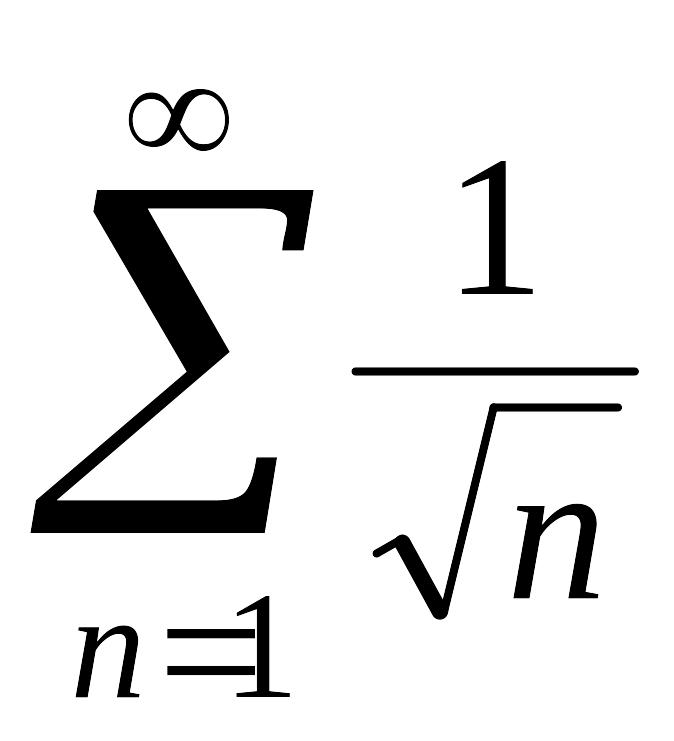 .
Имеем
.
Имеем
![]()
![]() Согласно признаку Даламбера сделать
заключение о сходимости или расходимости
ряда нельзя. Однако, как было показано
ранее (см. пример
2), этот ряд
расходится.
Согласно признаку Даламбера сделать
заключение о сходимости или расходимости
ряда нельзя. Однако, как было показано
ранее (см. пример
2), этот ряд
расходится.
Теорема
8
(признак
Коши).
Пусть дан
ряд
с положительными
членами и существует предел
![]() .
Тогда
а)
при
ряд сходится;
б)
при
ряд расходится.
.
Тогда
а)
при
ряд сходится;
б)
при
ряд расходится.
Пример 6.
Рассмотрим ряд
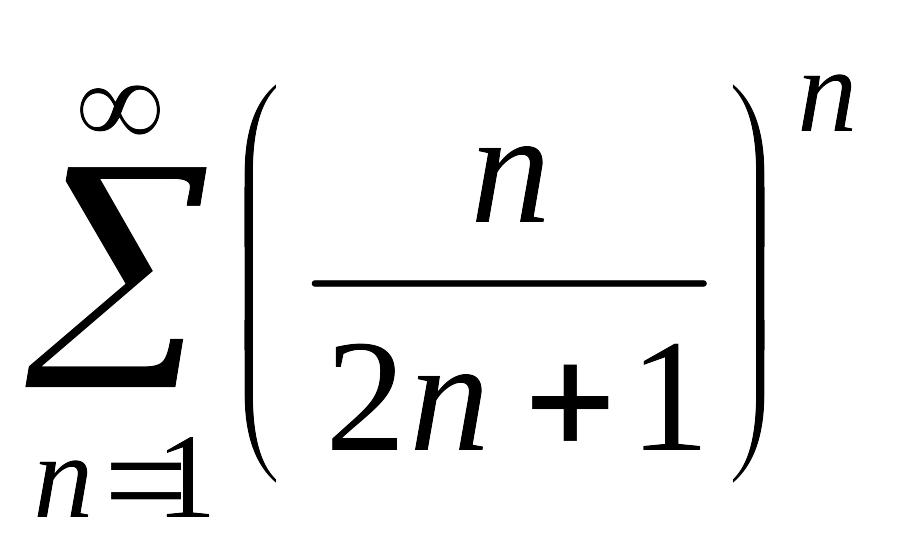 .
Имеем
.
Имеем
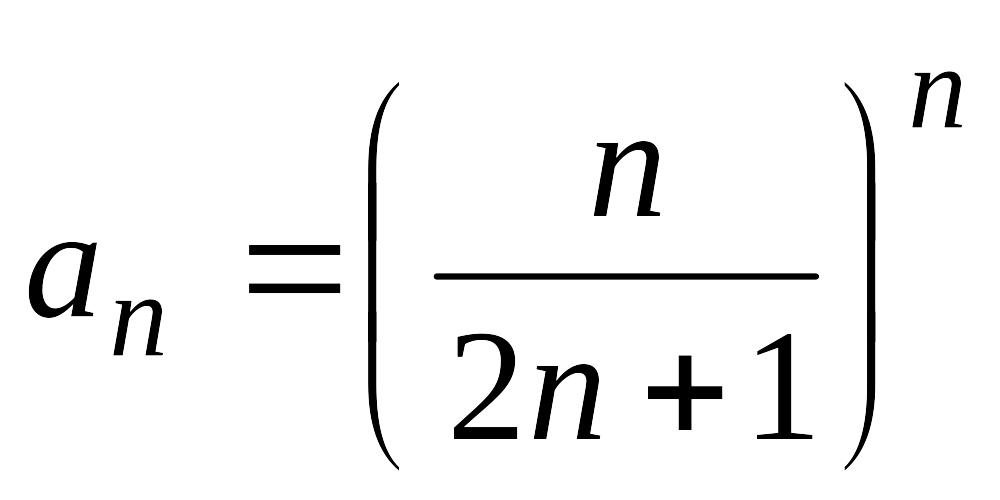 и
и
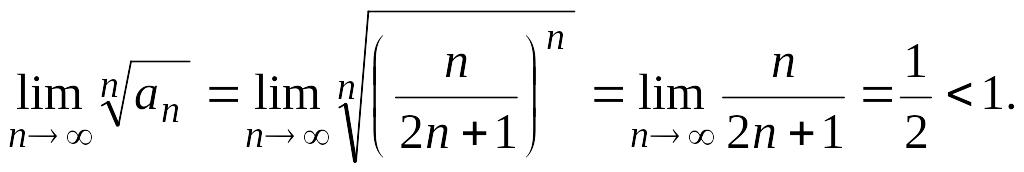 Согласно признаку Коши этот ряд сходится.
Согласно признаку Коши этот ряд сходится.
Теорема 9 (интегральный признак). Пусть дан ряд
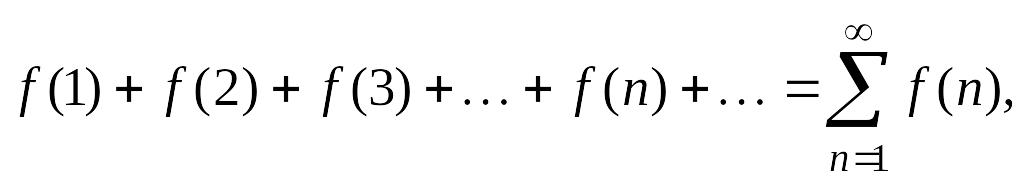
члены которого являются значениями некоторой функции
,
положительной, непрерывной и убывающей
на полуинтервале
![]() .
Тогда, если
.
Тогда, если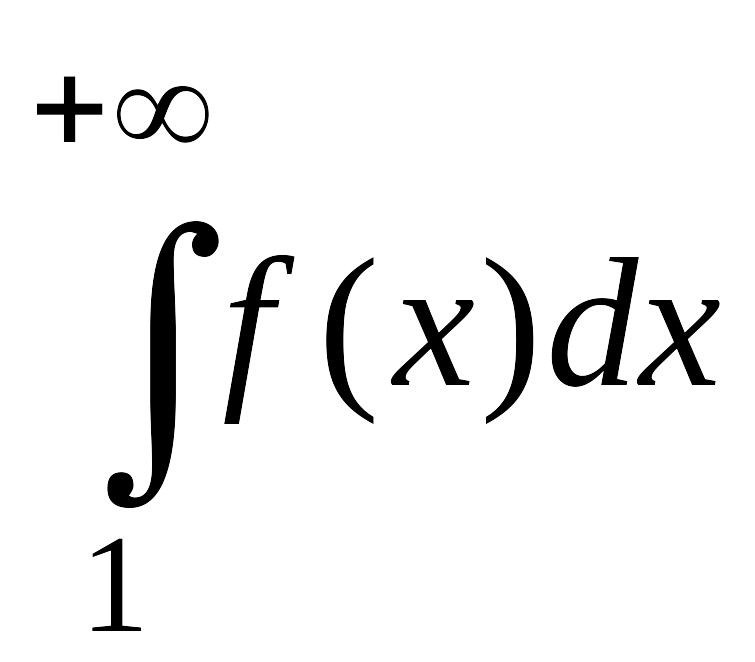 сходится,
то сходится и ряд
сходится,
то сходится и ряд
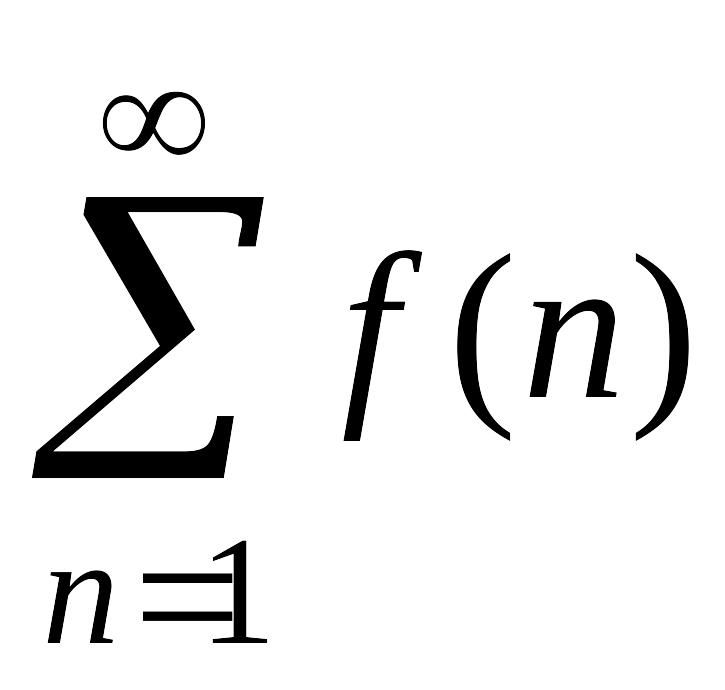 ;
если же
;
если же
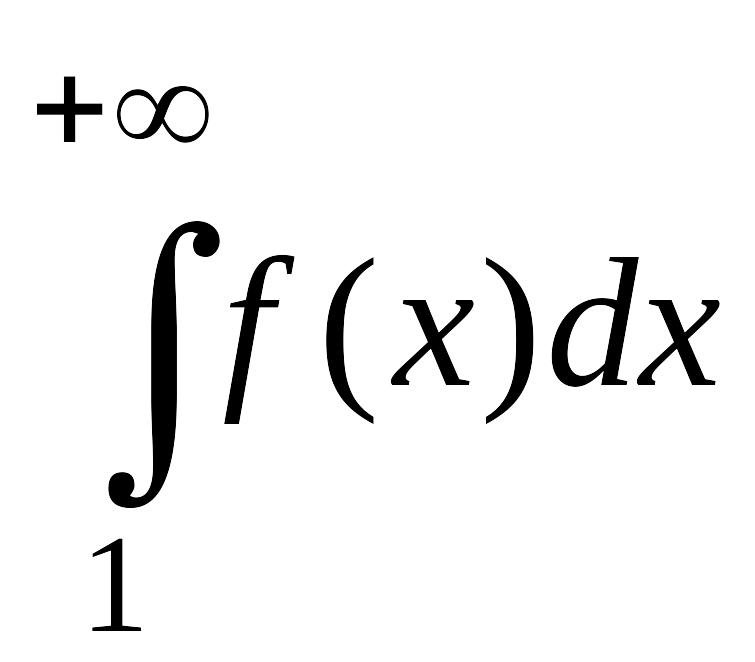 расходится,
то ряд
также расходится.
расходится,
то ряд
также расходится.
Пример 7. Рассмотрим ряд
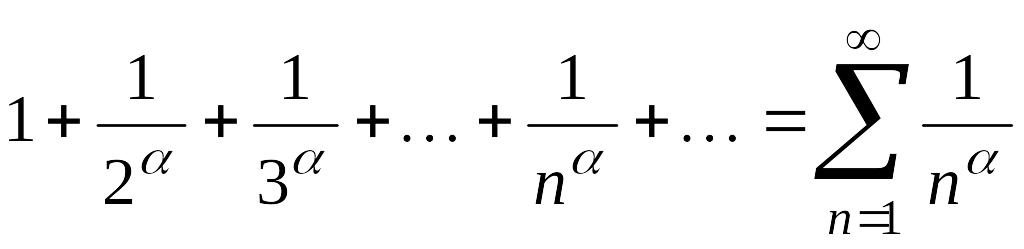 (
(![]() ).
).
С помощью
интегрального
признака
выясним поведение данного ряда при
.
Возьмем в качестве функции
функцию
![]() которая удовлетворяет условиям теоремы
8. Члены ряда равны значениям этой функции
при
которая удовлетворяет условиям теоремы
8. Члены ряда равны значениям этой функции
при
![]() .
Как известно,
несобственный интеграл
.
Как известно,
несобственный интеграл
![]() при
при
![]() сходится,
а при
сходится,
а при
![]() расходится. Следовательно, данный ряд
сходится при
и расходится при
.
расходится. Следовательно, данный ряд
сходится при
и расходится при
.
Заметим, что при
![]() такие ряды также расходятся, так как их
общий член не стремится к нулю при
такие ряды также расходятся, так как их
общий член не стремится к нулю при
![]() ,
т. е. нарушается необходимое условие
сходимости ряда (см. теорему
4).
,
т. е. нарушается необходимое условие
сходимости ряда (см. теорему
4).
В частности, при
![]() имеем сходящийся ряд
имеем сходящийся ряд
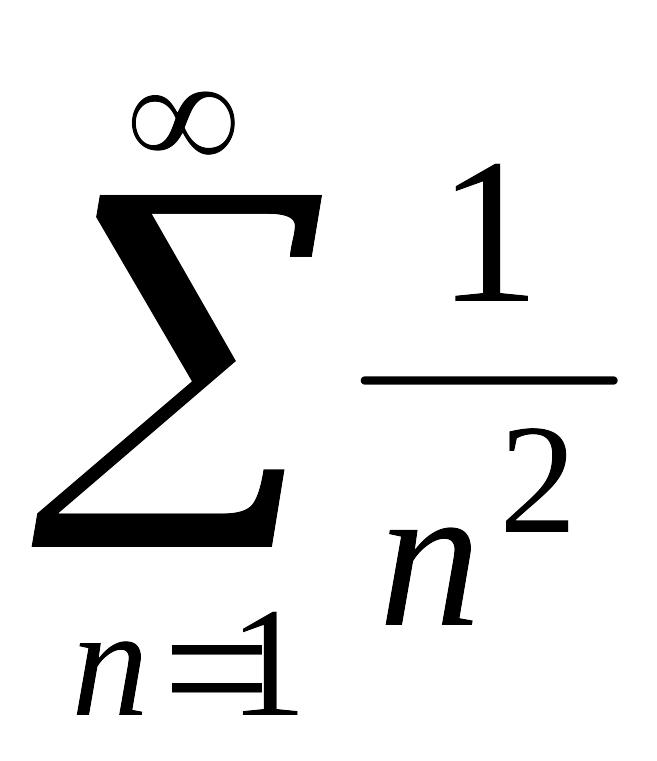 ;
;
при
расходящийся гармонический ряд
![]() ;
при
;
при
![]() pacходящийся
ряд
pacходящийся
ряд
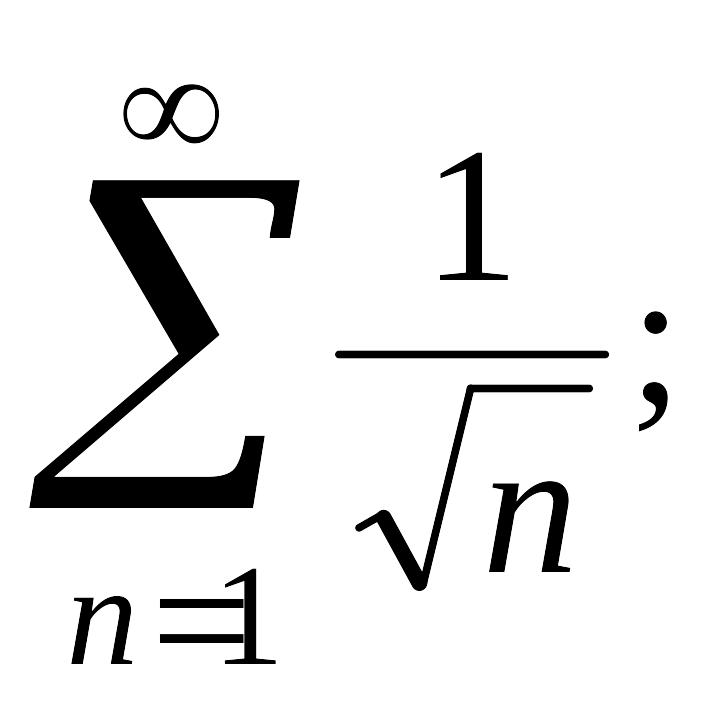 и т.д.
и т.д.
