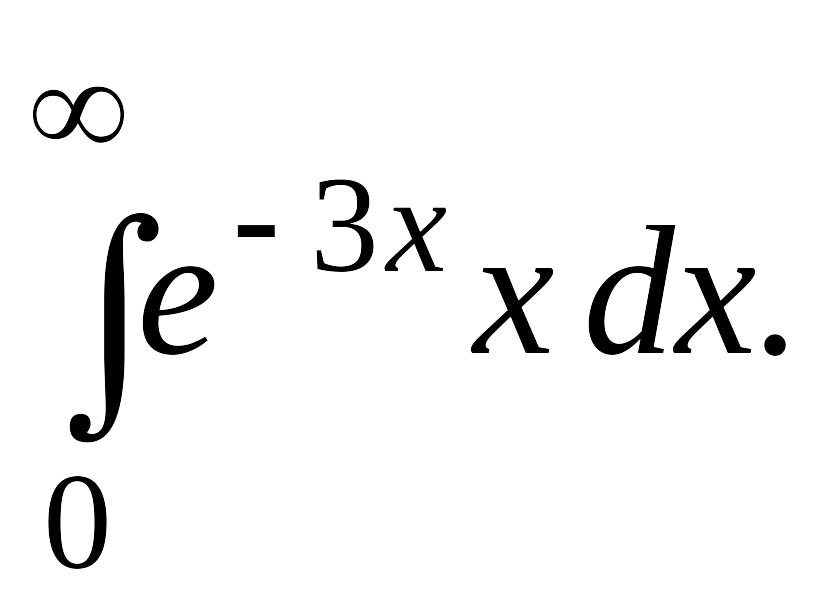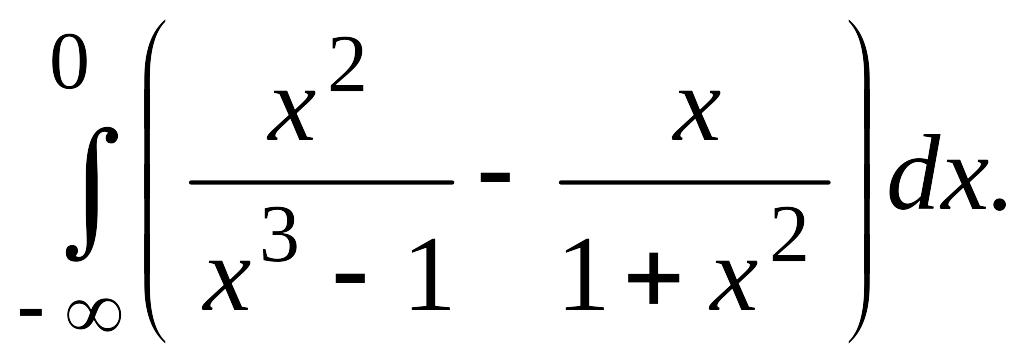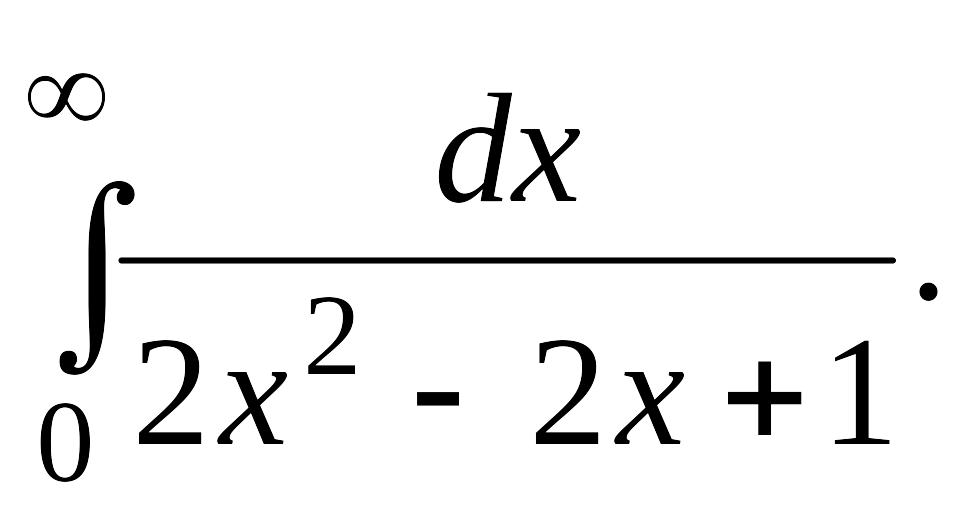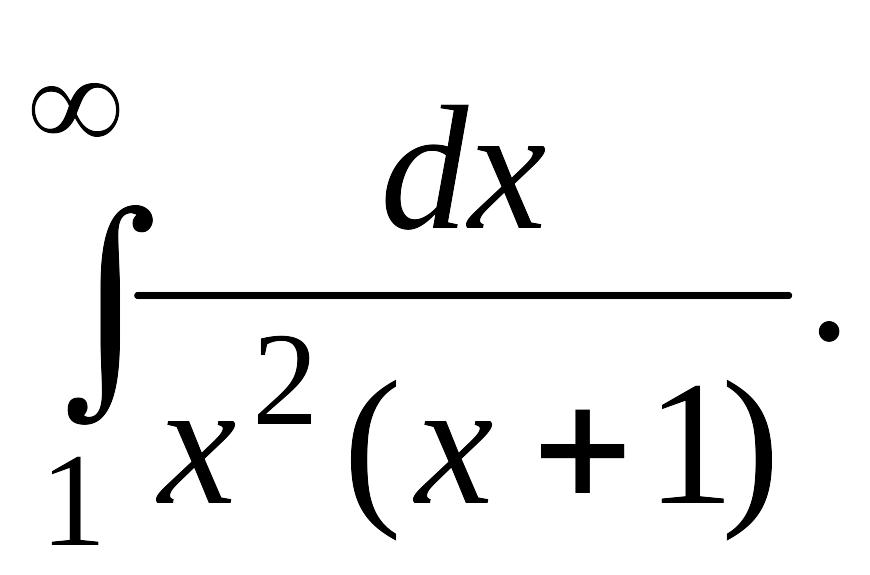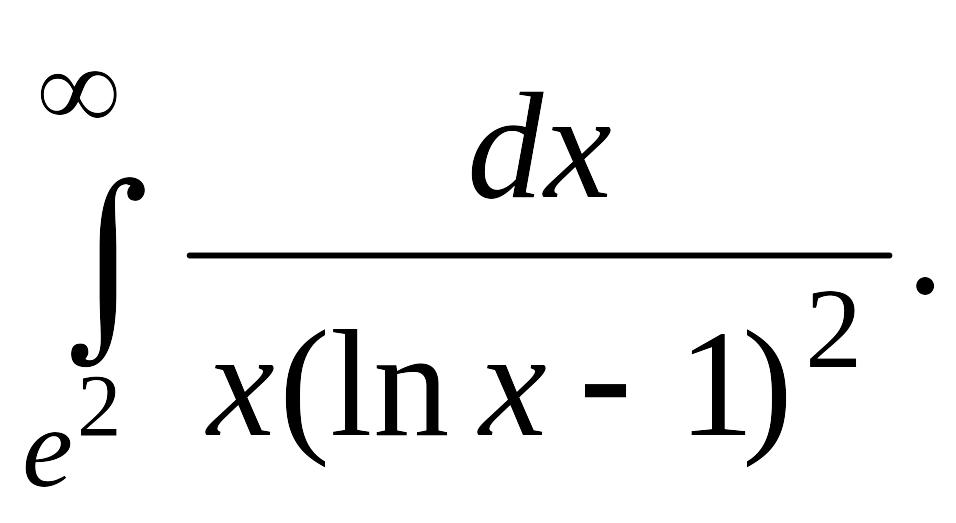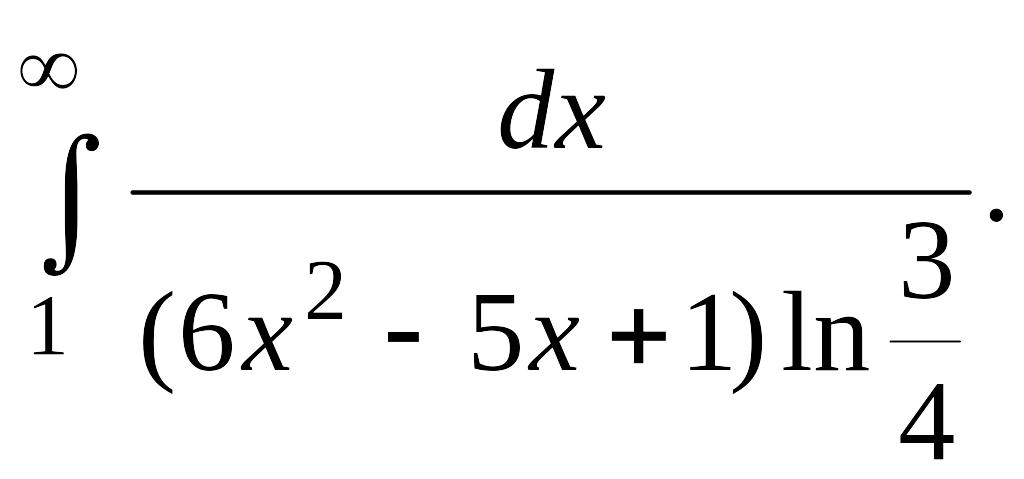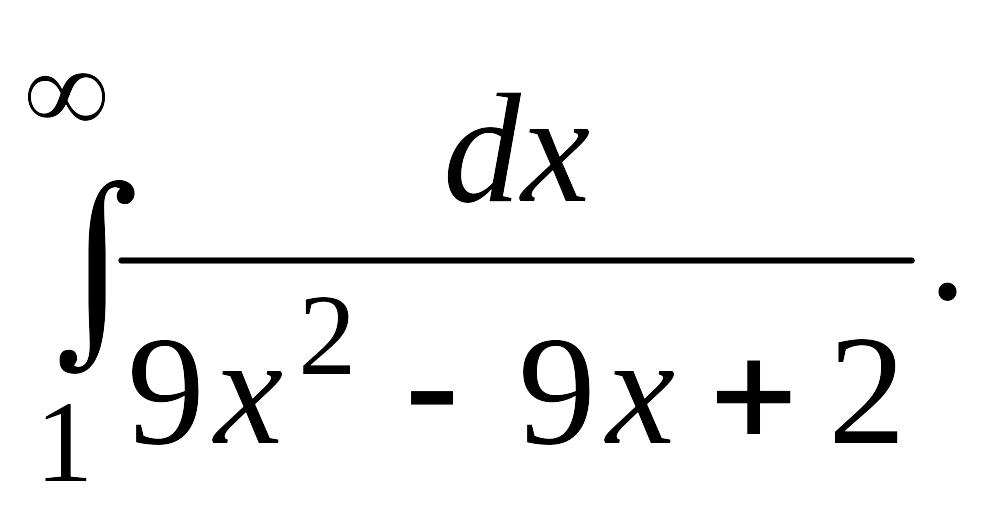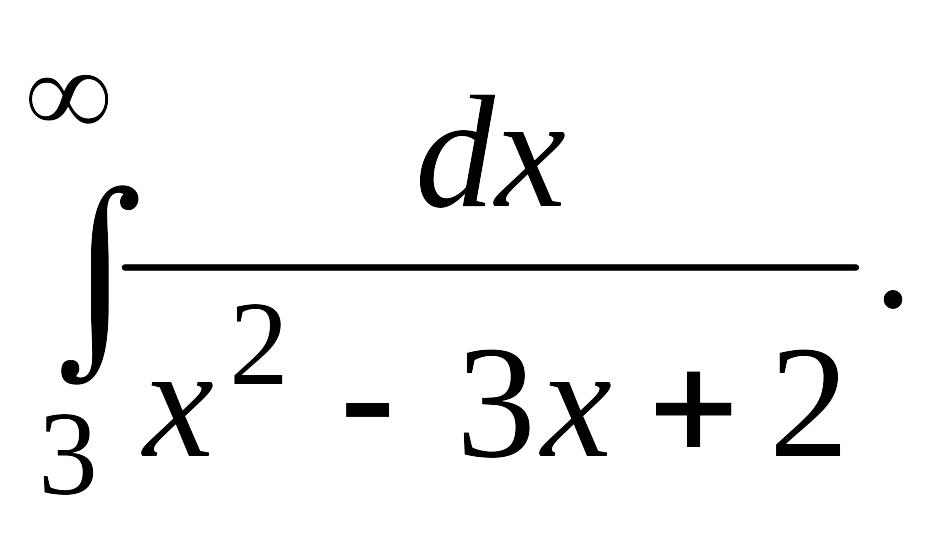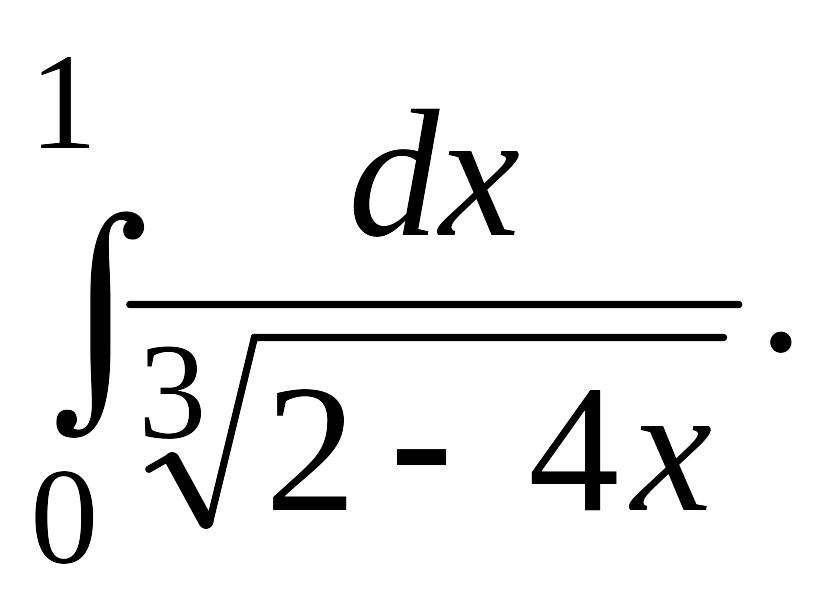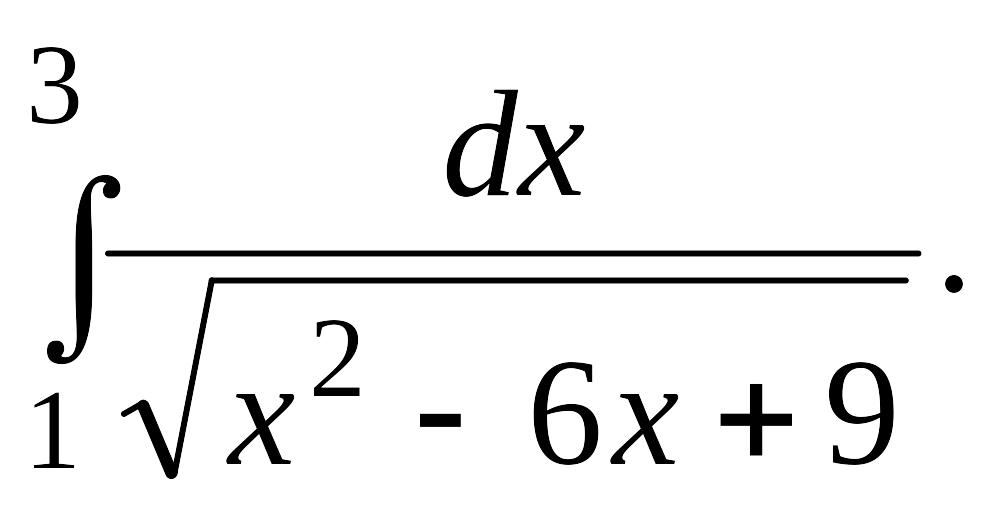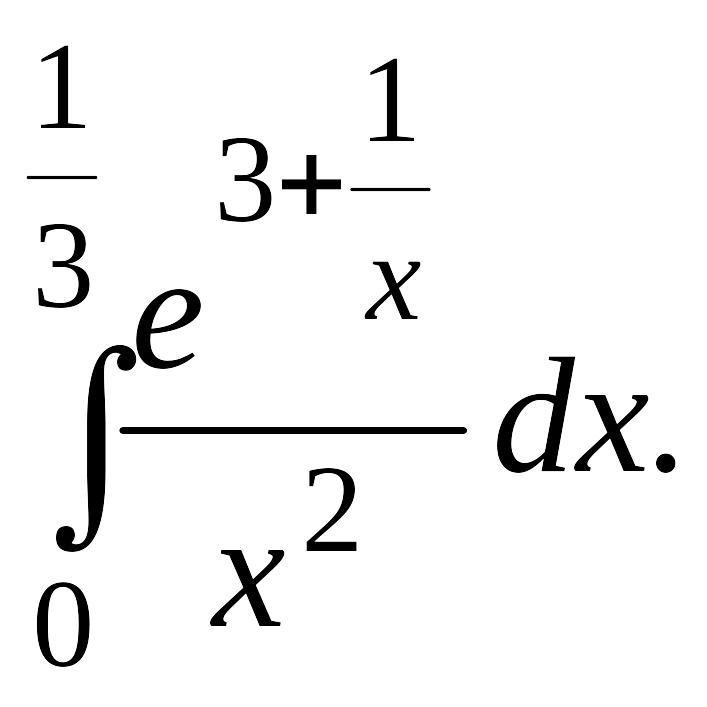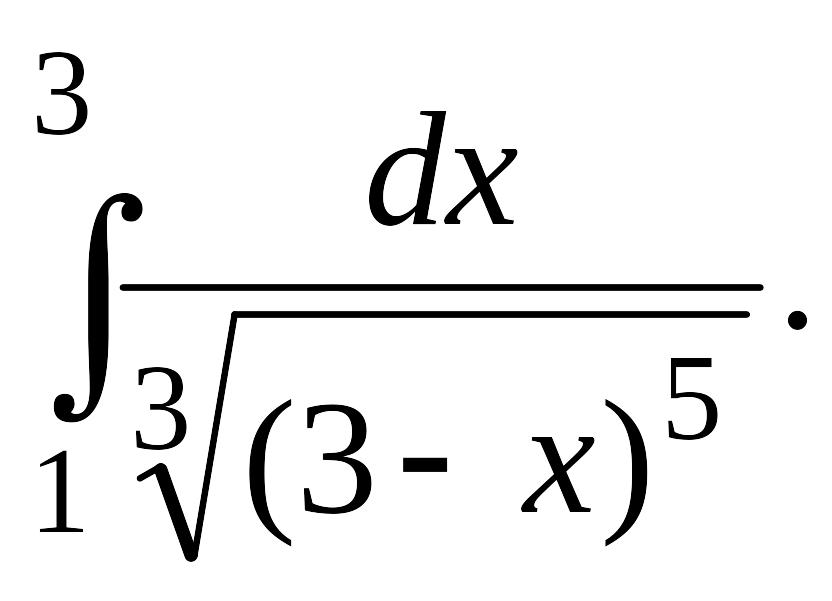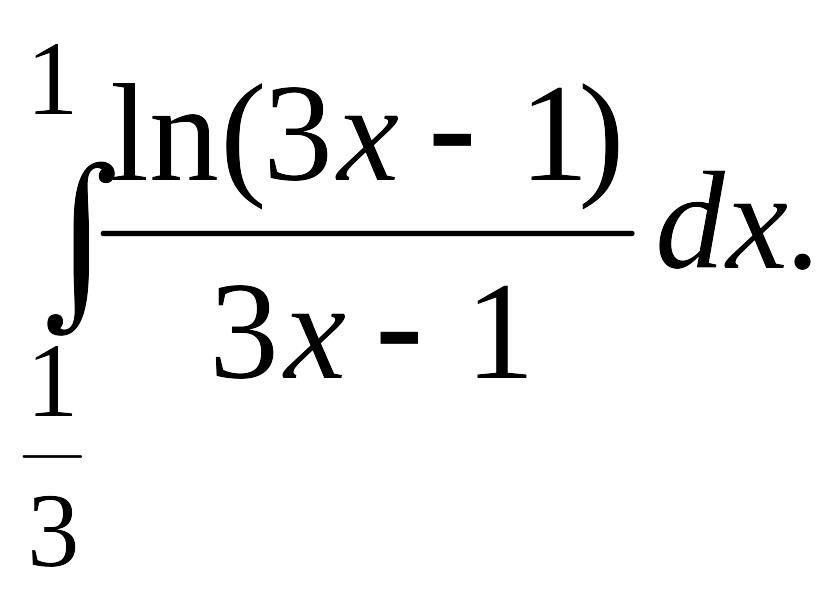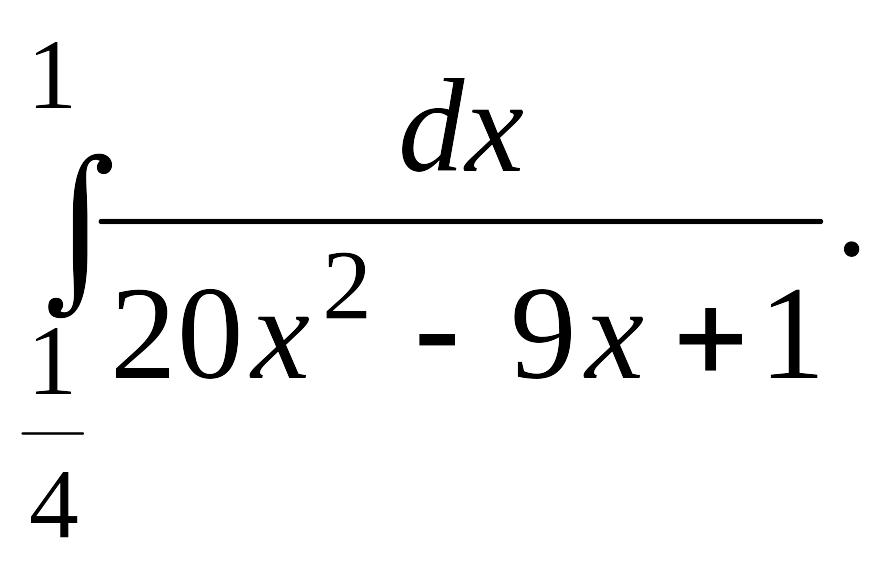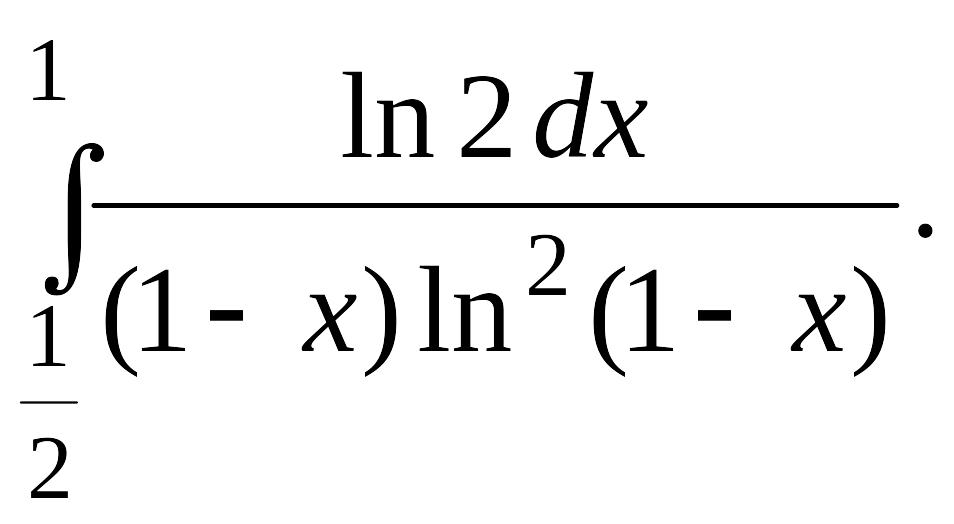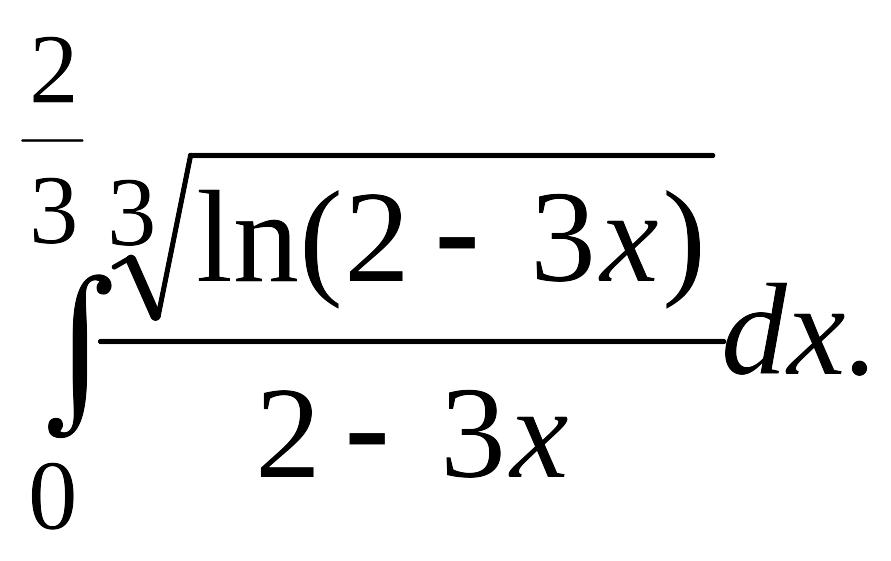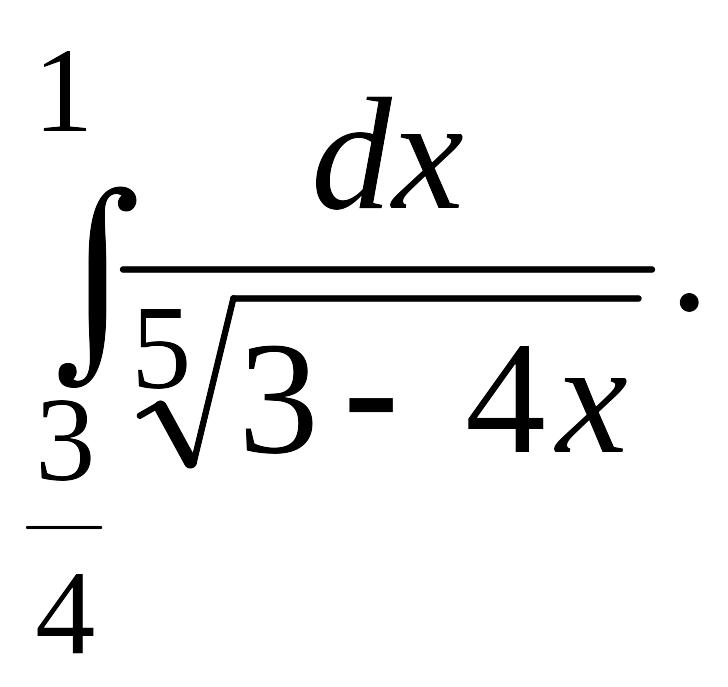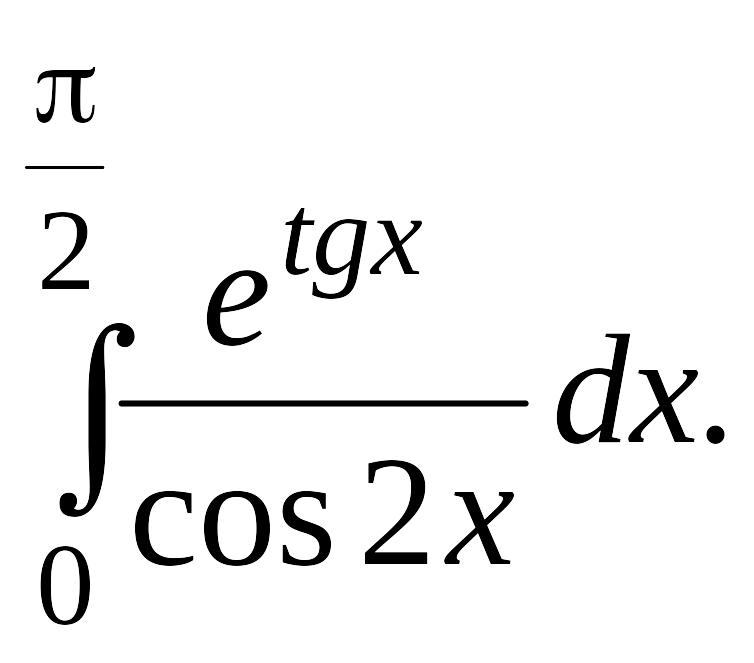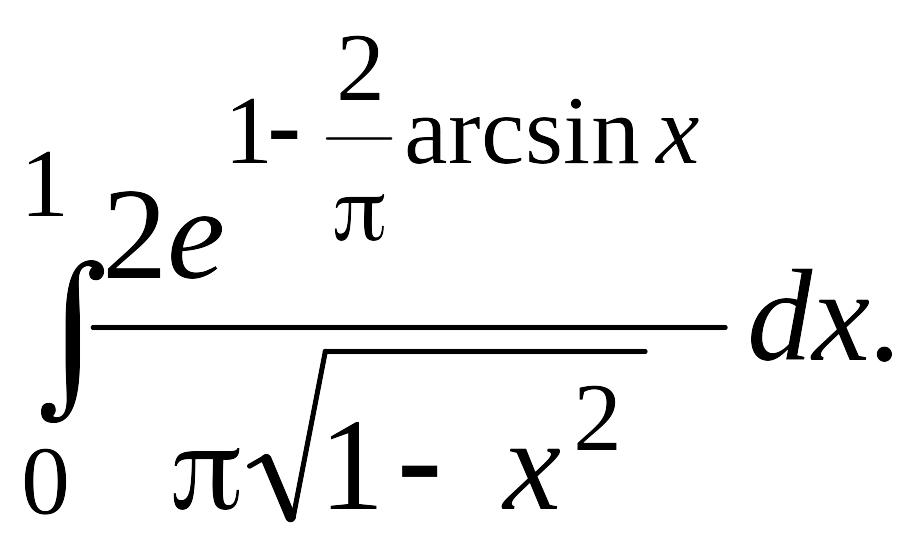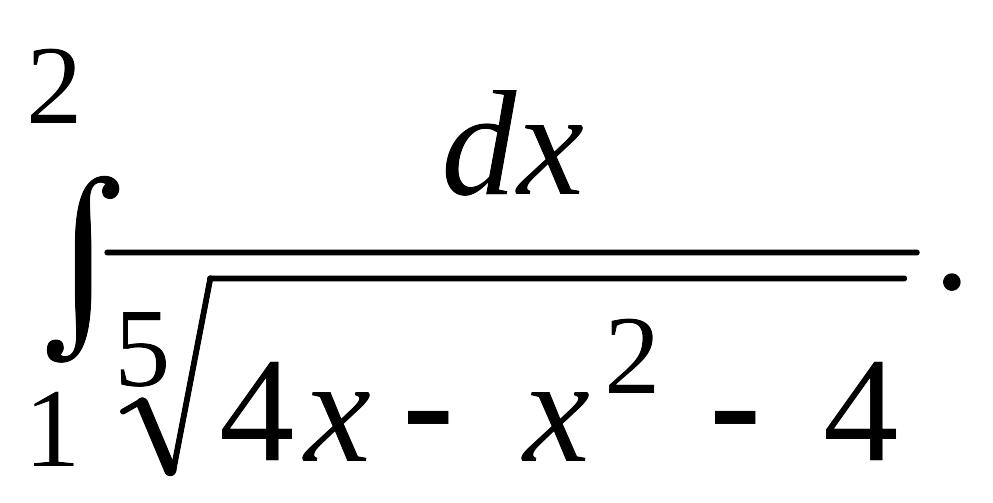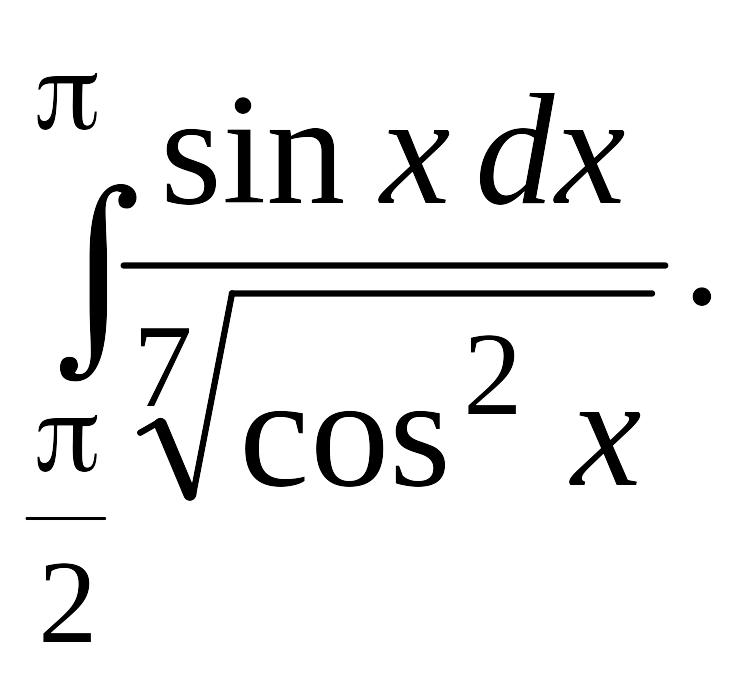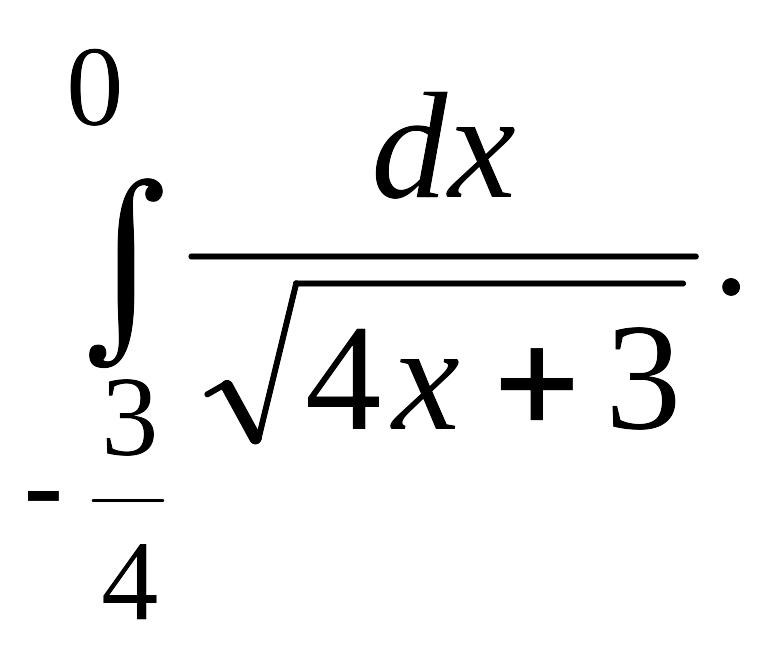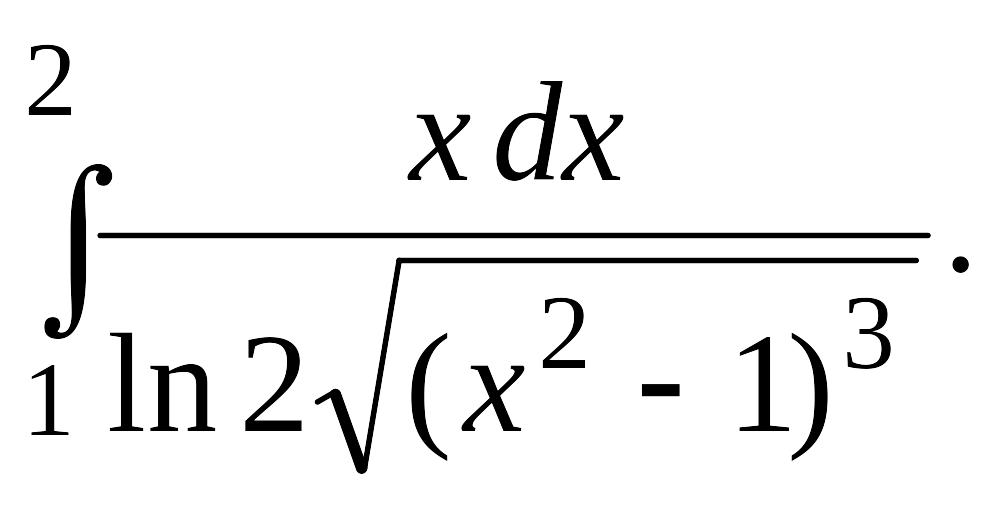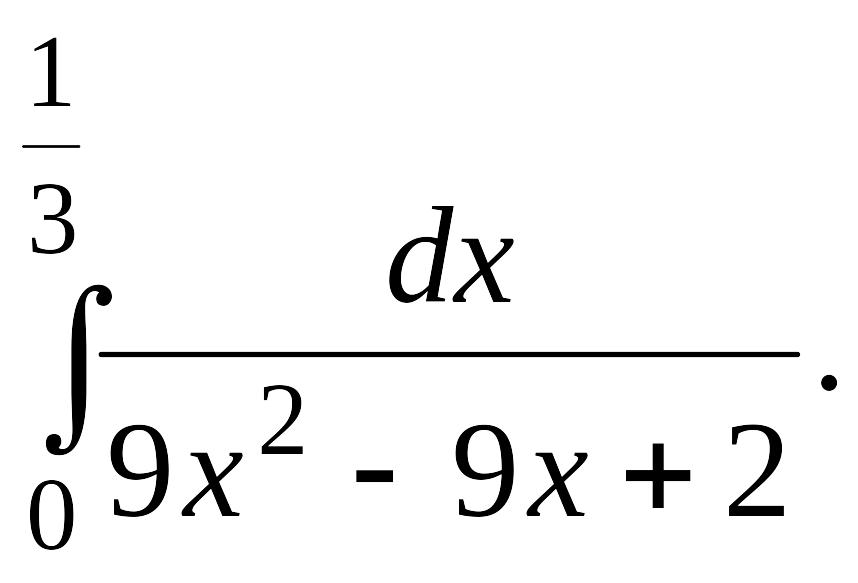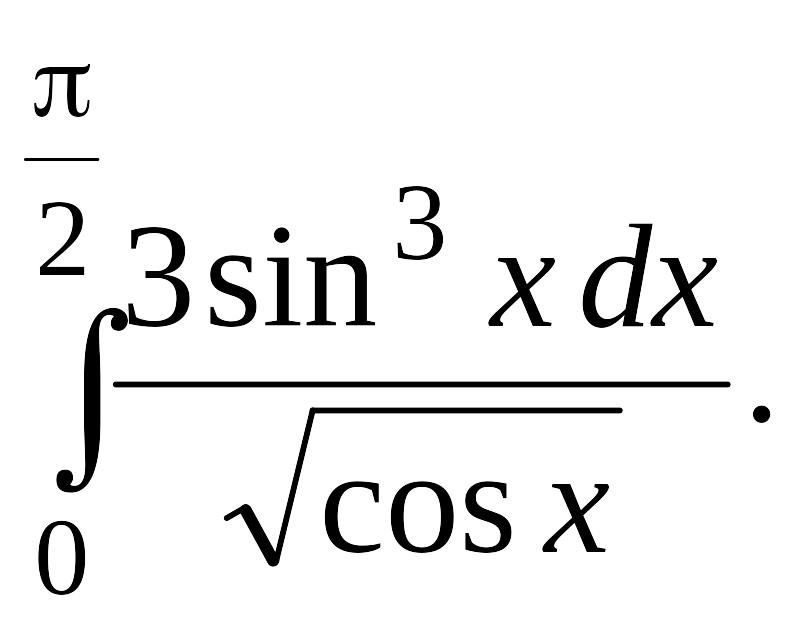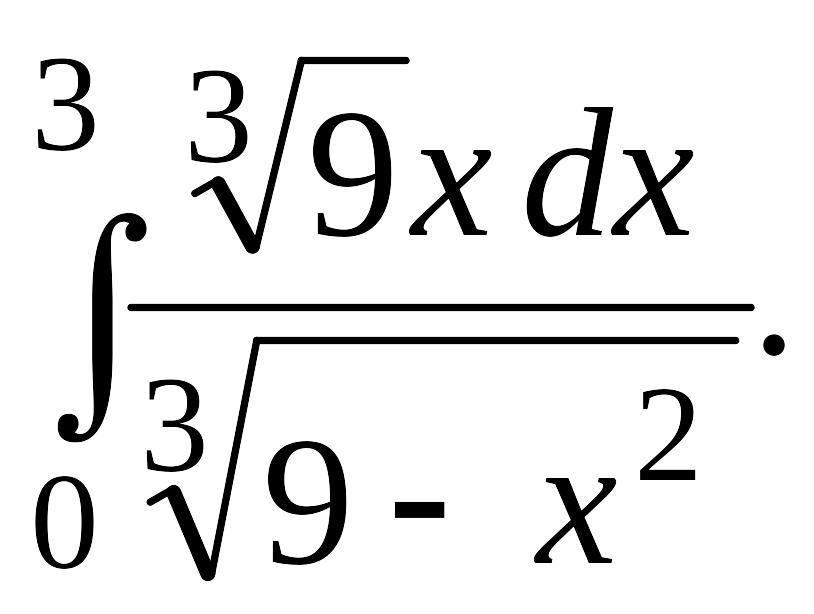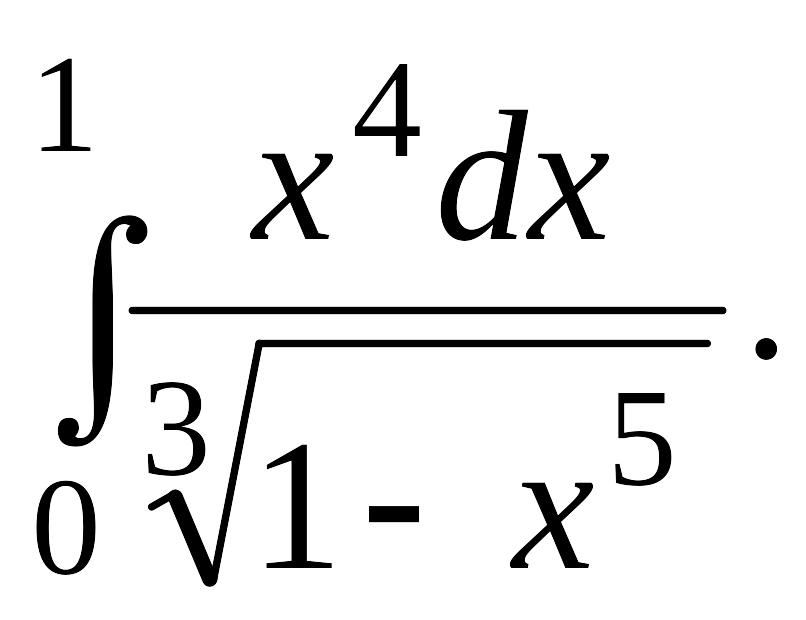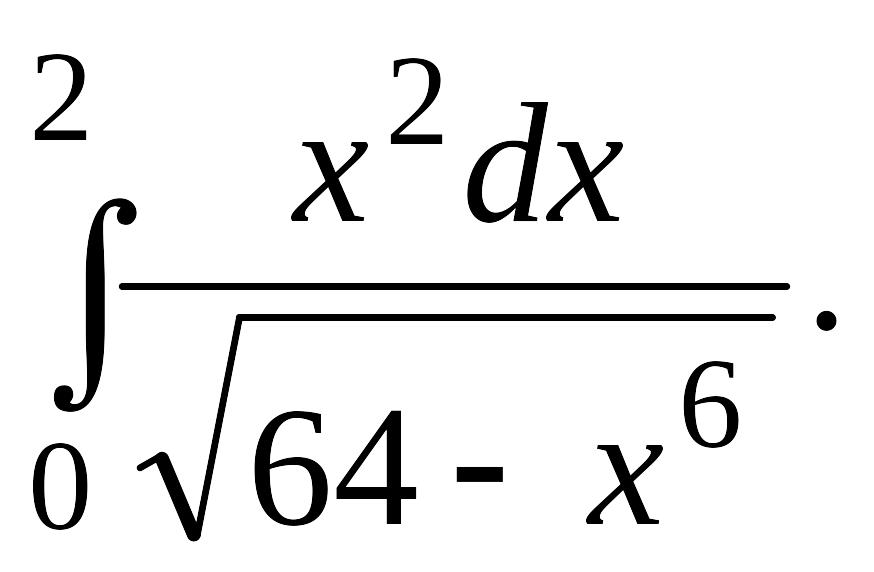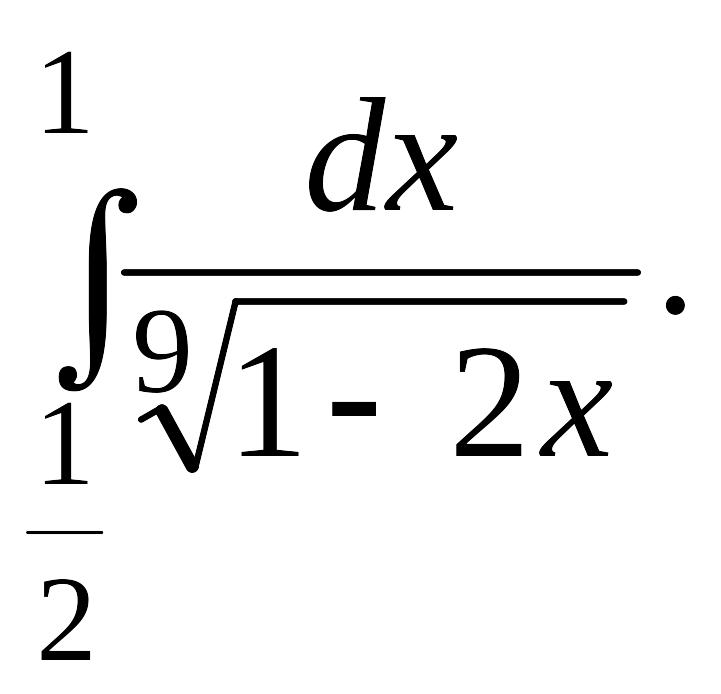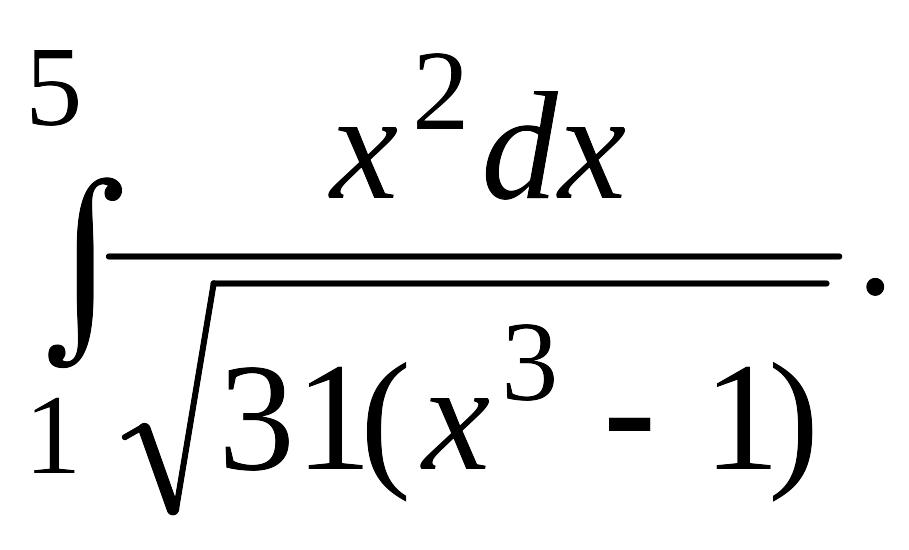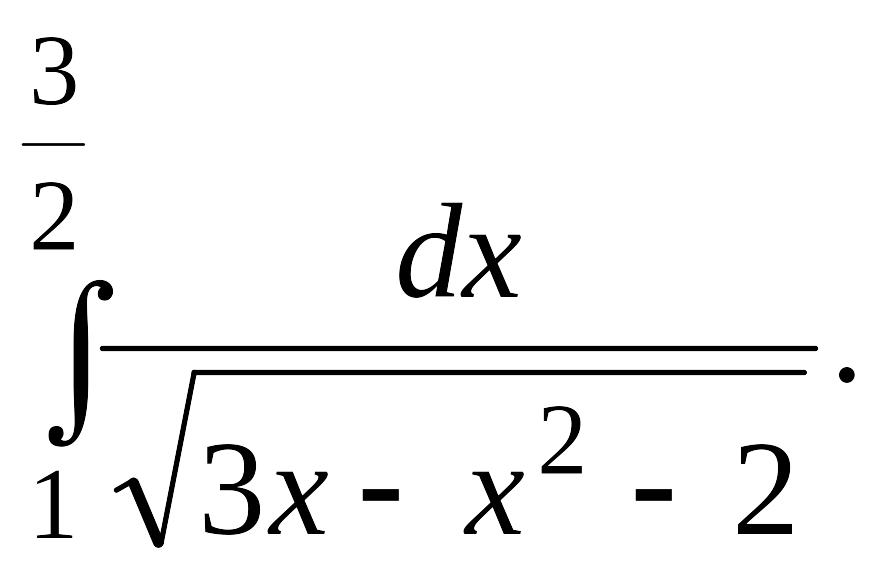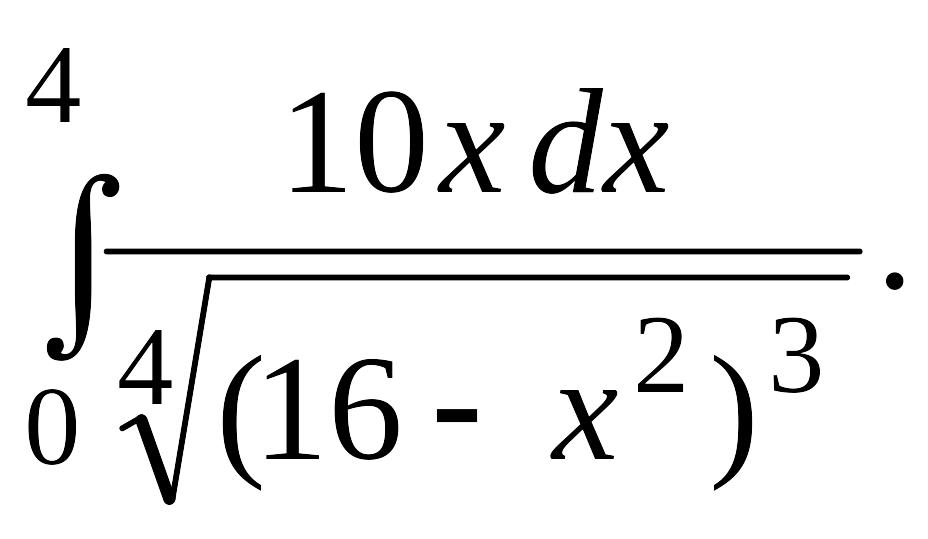- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко математический анализ
- •Часть 2
- •Учебное пособие
- •А.П. Бырдин н.В. Заварзин а.А. Сидоренко
- •Часть 2
- •Воронеж 2013
- •Введение
- •1. Комплексные числа и действия над ними
- •1.1. Комплексные числа. Основные определения
- •1.2. Основные действия над комплексными числами
- •1.3. Возведение в степень и извлечение корня из комплексного числа
- •1.4. Применение формул Эйлера и Муавра
- •1.5. Многочлены в комплексной области
- •Задачи к п. 1
- •Ответы к п.1
- •Неопределенный интеграл
- •2.1. Первообразная и неопределенный интеграл
- •2. Неопределенный интеграл.
- •2.2. Основные свойства неопределенного интеграла
- •2.3. Таблица основных интегралов
- •2.4. Основные методы интегрирования
- •Интегрирование рациональных функций
- •2.6. Интегрирование иррациональных и трансцендентных функций
- •Задачи к п. 2
- •Ответы к п. 2
- •Индивидуальные задания
- •3. Определенный интеграл
- •3.1. Определение определенного интеграла
- •Интегрируемость непрерывных и некоторых разрывных функций Теорема 1. Если функция непрерывна на отрезке то она интегрируема на нем.
- •3.3. Основные свойства определенного интеграла
- •Оценки интегралов. Формула среднего значения
- •2. Формула среднего значения.
- •Интеграл с переменным верхним пределом
- •3.6. Формула Ньютона-Лейбница
- •3.7. Замена переменной в определенном интеграле
- •Пример 1. Вычислить
- •Формула интегрирования по частям в определенном интеграле
- •Некоторые физические и геометрические приложения определенного интеграла
- •3.10. Несобственные интегралы
- •1. Несобственные интегралы с бесконечными пределами интегрирования.
- •2. Несобственные интегралы от неограниченных функций.
- •Задачи к п. 3
- •Ответы к п. 3
- •3.11. Индивидуальные задания
- •Задача 4.
- •Задача 5.
- •Задача 6.
- •4. Ряды
- •4.1. Понятие числового ряда
- •Суммы конечного числа членов ряда
- •2. Свойства сходящихся рядов.
- •Ряды с неотрицательными членами
- •4.3. Знакочередующиеся ряды
- •4.4. Абсолютная и условная сходимость рядов
- •Возьмем какой-нибудь знакопеременный ряд
- •4.5. Степенные ряды
- •Таким образом, при любом х имеет место разложение
- •4.6. Ряды Фурье
- •Задачи к п. 2
- •Ответы к п. 2
- •Библиографический список
- •8. Краснов м.Л. Функции комплексного переменного. Операционное исчисление. Теория устойчивости / м.Л. Краснов, а.И. Киселев, г.И. Макаренко – м.: Наука, 1981. Оглавление
- •1. Комплексные числа и действия над ними …………….4
- •Неопределенный интеграл ……………………......…...23
- •3. Определенный интеграл.….……………....………........68
- •4. Ряды……..…………................………………...…...…...118
- •Бырдин Аркадий Петрович
- •Часть 2
- •394026 Воронеж, Московский просп., 14
Ответы к п. 3
1.
![]() 2.
6. 3.
ln2.
4.
e(e
– 1).
2.
6. 3.
ln2.
4.
e(e
– 1).
5.
1/3. 6.
2. 7.
![]() 8.
1. 9.
8.
1. 9.
![]()
10.
![]() 11.
11.
![]() 12.
21/8. 13.
12.
21/8. 13.
![]()
14.
10/3. 15.
0. 16.
![]() .
17.
1. 18.
аrctg
2.
.
17.
1. 18.
аrctg
2.
19.
e
– 2. 20.
![]() 21.
0. 22.
21.
0. 22.
![]() 23.
23.
![]()
24.
![]() 25.
25.
![]() 26.
2ln2 – 1. 27.
26.
2ln2 – 1. 27.
![]()
28.
2 – ln2. 29.
1/3. 30.
1/3. 31.
![]() 32.
32.
![]() 33.
33.
![]() .
34.
1/2. 35.
.
34.
1/2. 35.
![]() 36.
36.
![]() 37.
32/3. 38.
37.
32/3. 38.
![]() 39.
1. 40.
8/3. 41.
4/3. 42.
1/2. 43.
11/2. 44.
39.
1. 40.
8/3. 41.
4/3. 42.
1/2. 43.
11/2. 44.
![]() 45.
1/2. 46.
45.
1/2. 46.
![]() 47.
47.
![]() .
.
48.
![]() 49.
1/3. 50.
4. 51.
9. 52.
9/4. 53.
49.
1/3. 50.
4. 51.
9. 52.
9/4. 53.
![]() 54.
54.
![]() 55.
55.
![]() 56.
56.
![]() 57.
57.
![]() 58.
58.
![]() 59.
14/3.
59.
14/3.
60.
![]() 61.
61.![]() .
62.
6a.
63.
8a.
.
62.
6a.
63.
8a.
64.
![]() 65.
65.
![]() 66.
66.
![]() 67.
67.
![]() 68.
68.
![]() 69.
69.
![]() 70.
70.![]()
71.![]()
72.
![]()
73.
![]() .
74.
.
74.
![]() 75.
75.
![]()
76.
![]() 77.
77.
![]()
78.
![]() 79.
79.
![]() 80.
80.
![]()
81.
![]() 82.
82.
![]() 83.
83.
![]()
84.
![]() 85.
A
= 0,125 кгм.
86.
85.
A
= 0,125 кгм.
86.
![]() 87.
87.
![]() 88.
88.
![]() 89.
1. 90.
1/2. 91.
ln2. 92.
Расходится.
89.
1. 90.
1/2. 91.
ln2. 92.
Расходится.
93.
Расходится. 94.
Расходится. 95.
1.
96.
![]() при
при
![]() расходится при
97.
расходится при
97.
![]() 98.
1.
99.
1. 100.
98.
1.
99.
1. 100.
![]() 101.
101.
![]() 102.
102.
![]()
3.11. Индивидуальные задания
Вычислить определенные интегралы с точностью до двух знаков после запятой.
Задача 1.
1.1. |
|
1.2.
|
1.3. |
|
1.4.
|
1.5. |
|
1.6.
|
1.7. |
|
1.8.
|
1.9. |
|
1.10.
|
1.11. |
|
1.12.
|
1.13. |
|
1.14.
|
1.15. |
|
1.16.
|
1.17. |
|
1.18.
|
1.19. |
|
1.20.
|
1.21. |
|
1.22.
|
1.23. |
|
1.24.
|
1.25. |
|
1.26.
|
1.27. |
|
1.28.
|
1.29. |
|
1.30.
|
В задачах 2, 3 вычислить несобственные интегралы или доказать их расходимость.
Задача 2.
12 |
|
2.2.
|
2.3. |
|
2.4.
|
2.5. |
|
2.6.
|
2.7. |
|
2.8.
|
2.9. |
|
2.10.
|
2.11. |
|
2.12.
|
2.13. |
|
2.14.
|
2.15. |
|
2.16.
|
2.17. |
|
2.18.
|
2.19. |
|
2.20.
|
2.21. |
|
2.22.
|
2.23. |
|
2.24.
|
2.25. |
|
2.26.
|
2.27. |
|
2.28.
|
2.29. |
|
2.30.
|
Задача 3.
3.1. |
|
3.2.
|
3.3. |
|
3.4.
|
3.5. |
|
3.6.
|
3.7. |
|
3.8.
|
14 |
|
3.10.
|
3.11. |
|
3.12.
|
3.13. |
|
3.14.
|
3.15. |
|
3.16.
|
3.17. |
|
3.18.
|
3.19. |
|
3.20.
|
3.21. |
|
3.22.
|
3.23. |
|
3.24.
|
3.25. |
|
3.26.
|
3.27. |
|
3.28.
|
3.29. |
|
3.30.
|

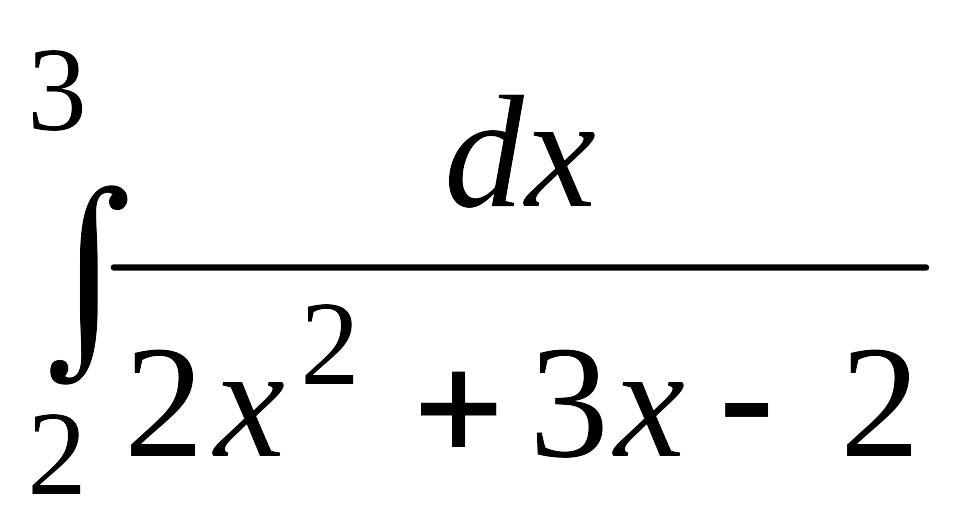 .
.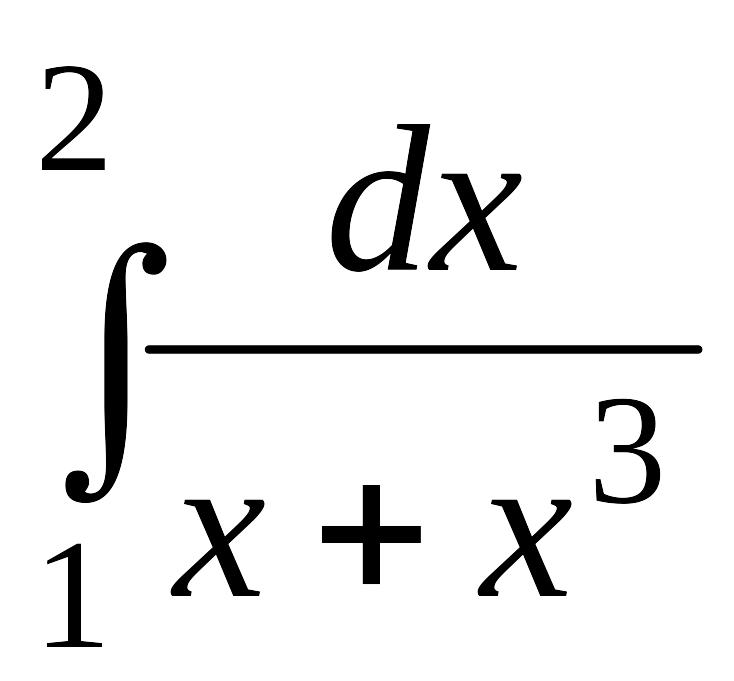 .
.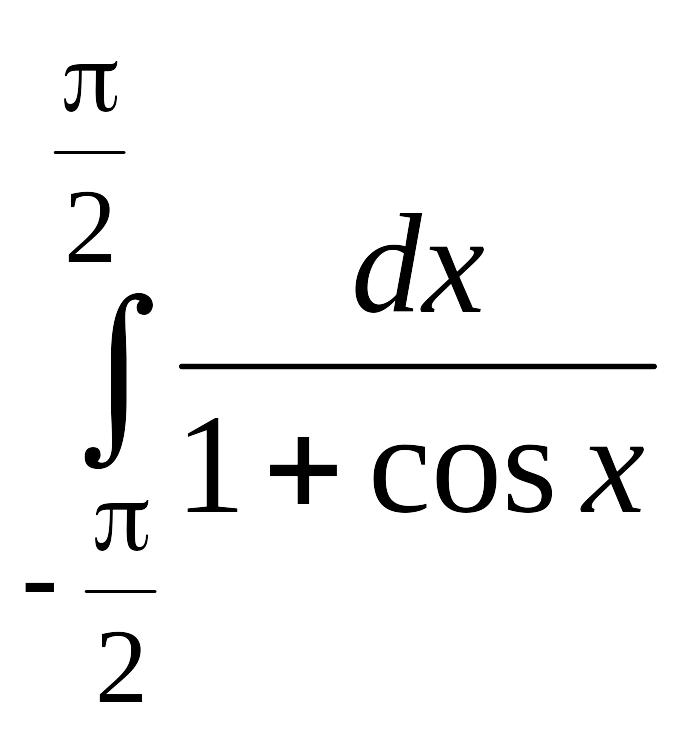 .
.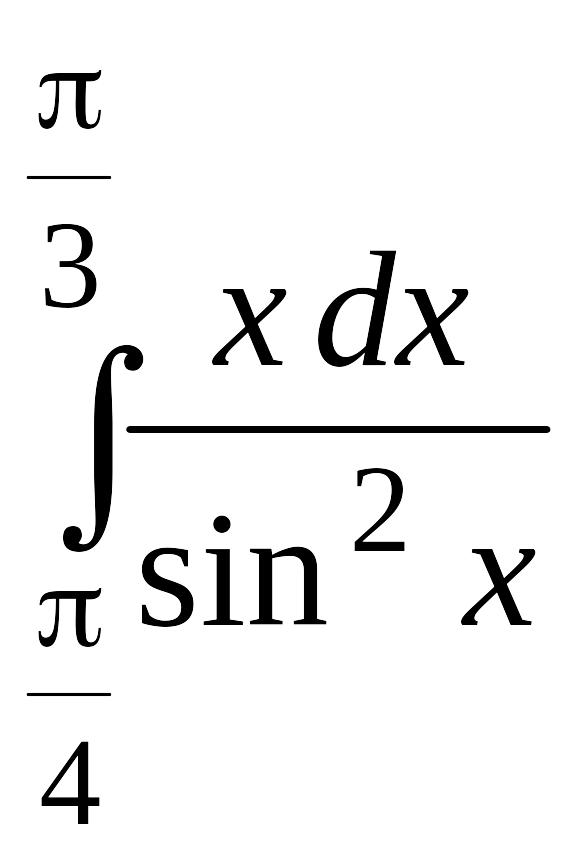 .
.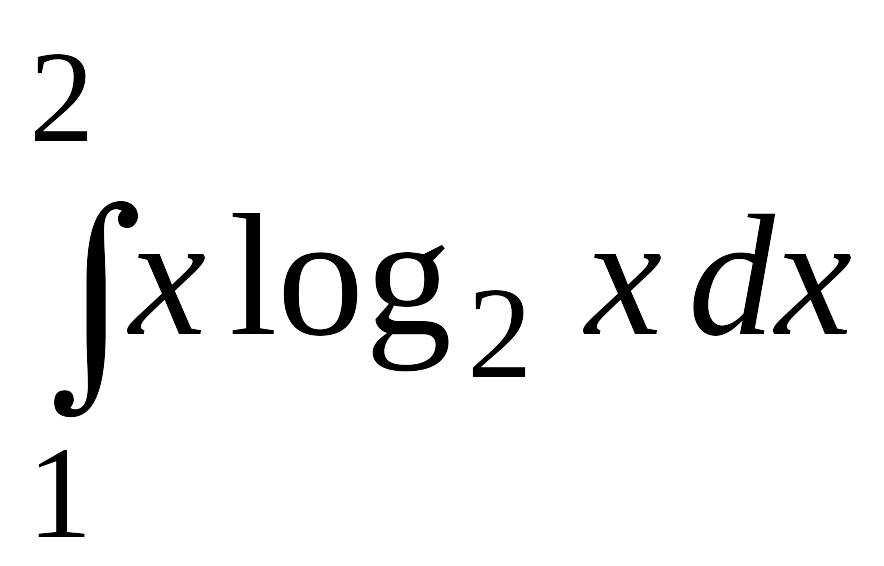 .
.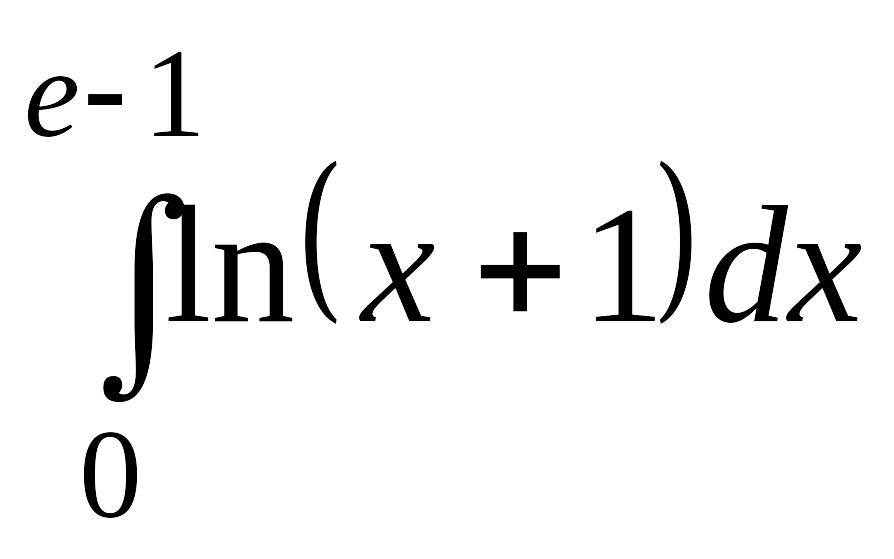 .
.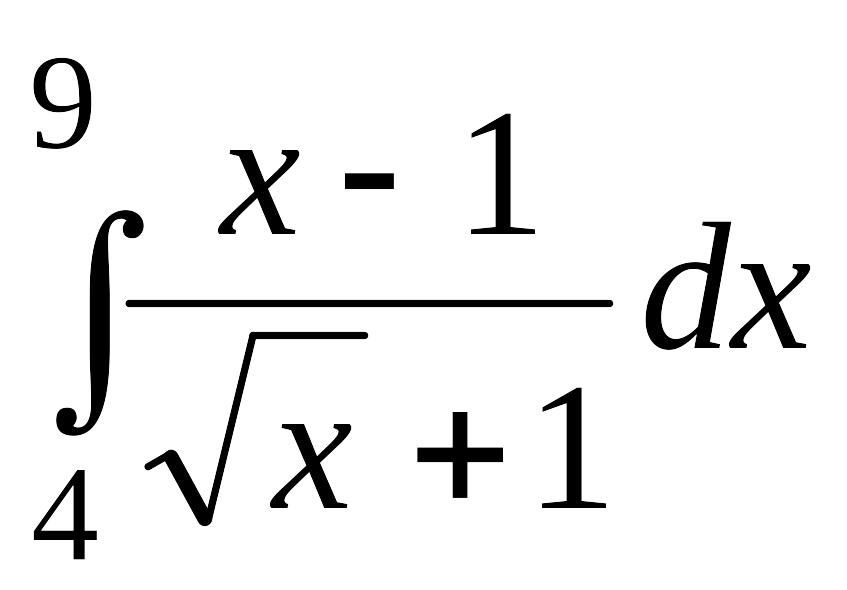 .
.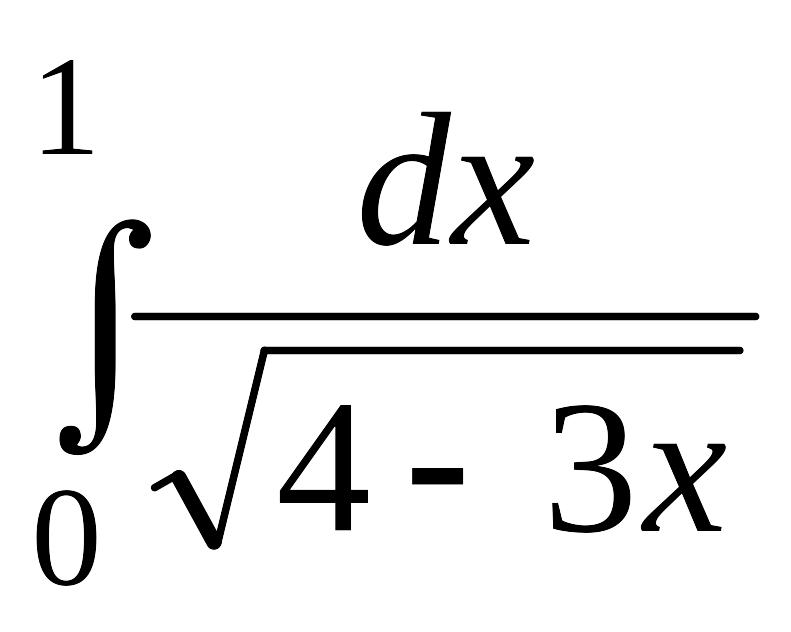 .
.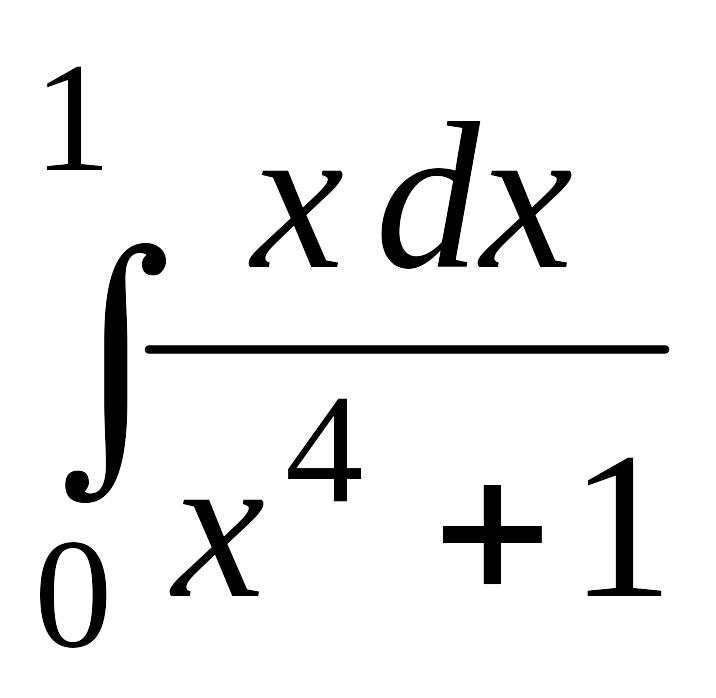 .
.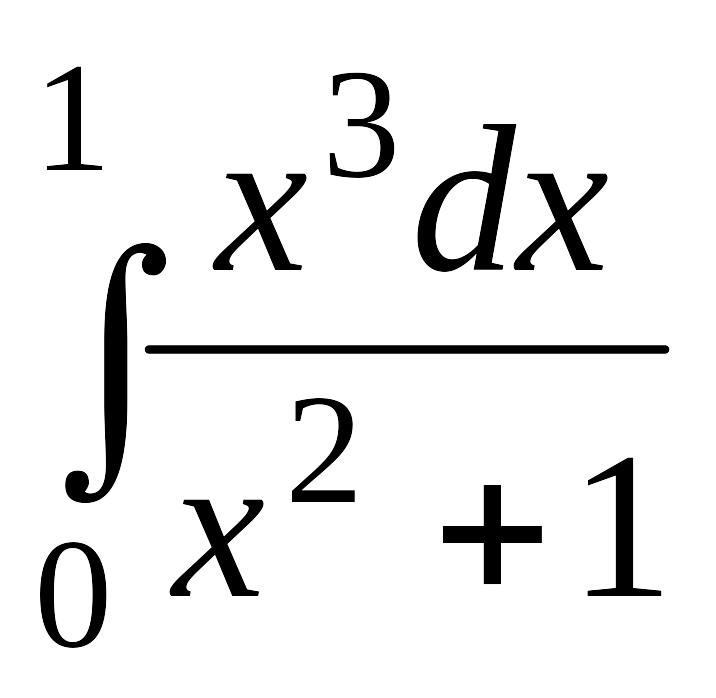 .
.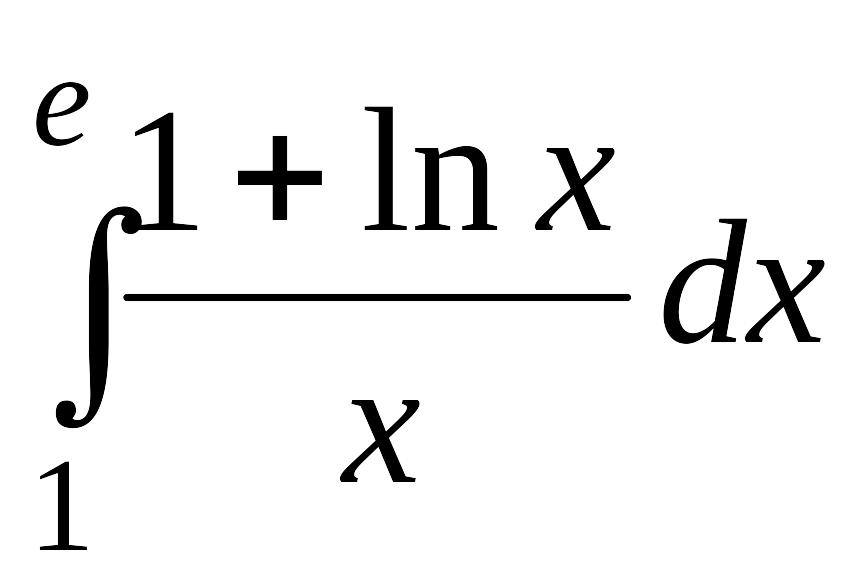 .
.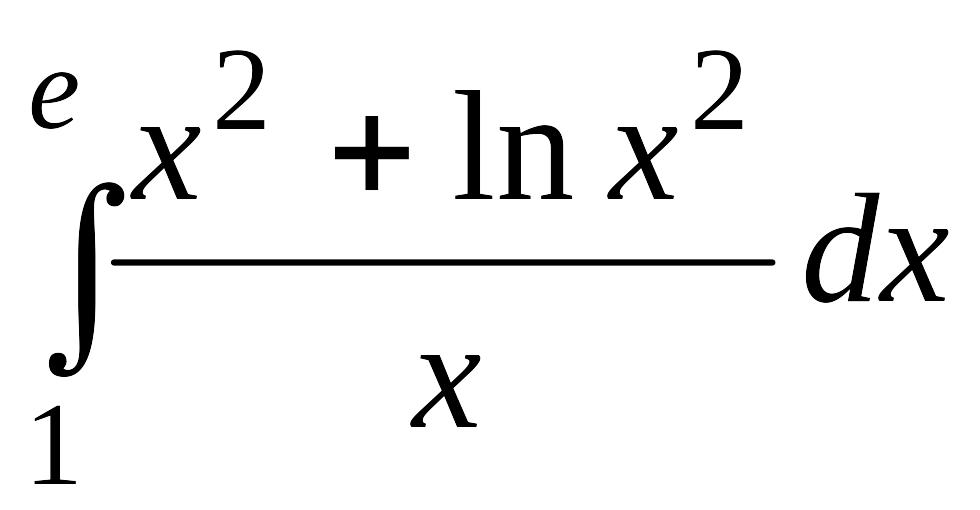 .
.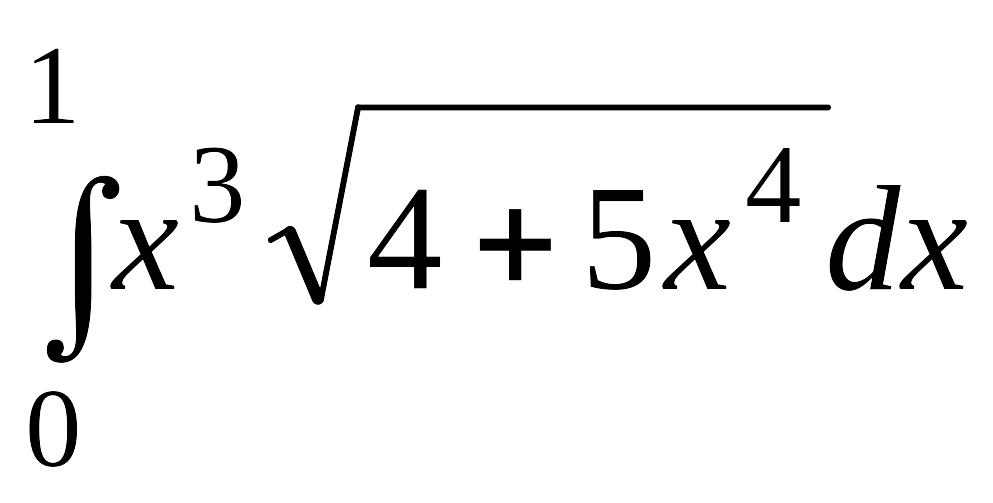 .
.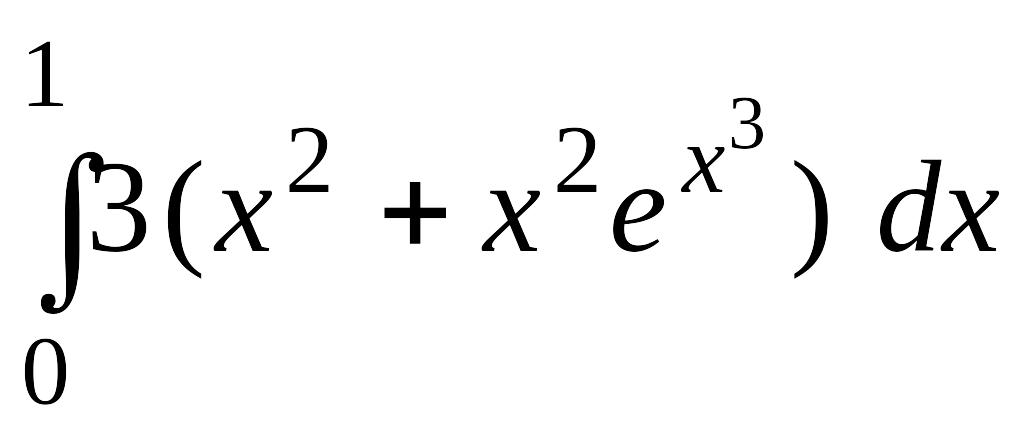 .
.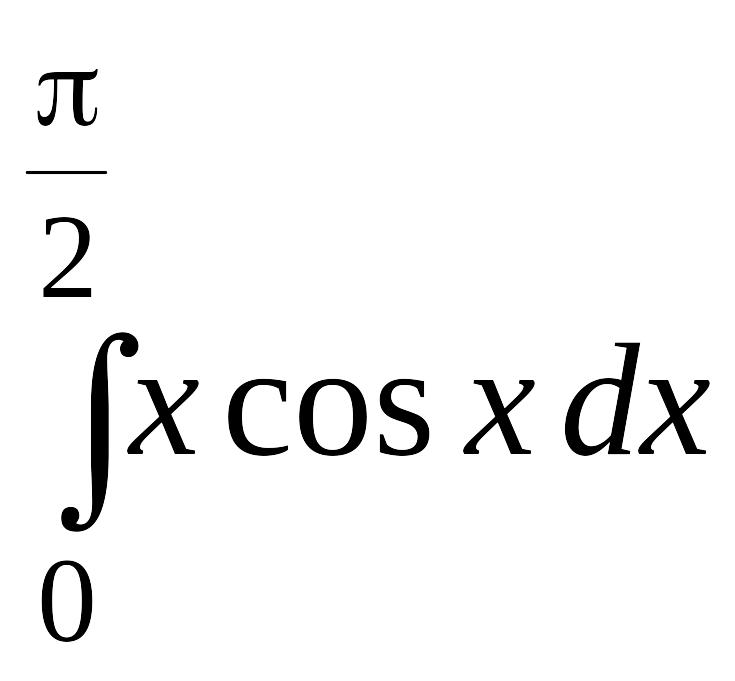 .
.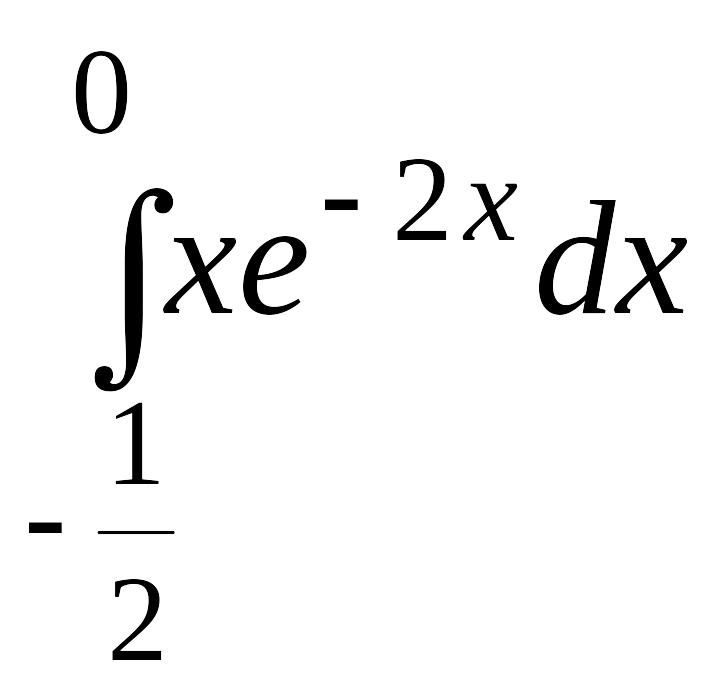 .
.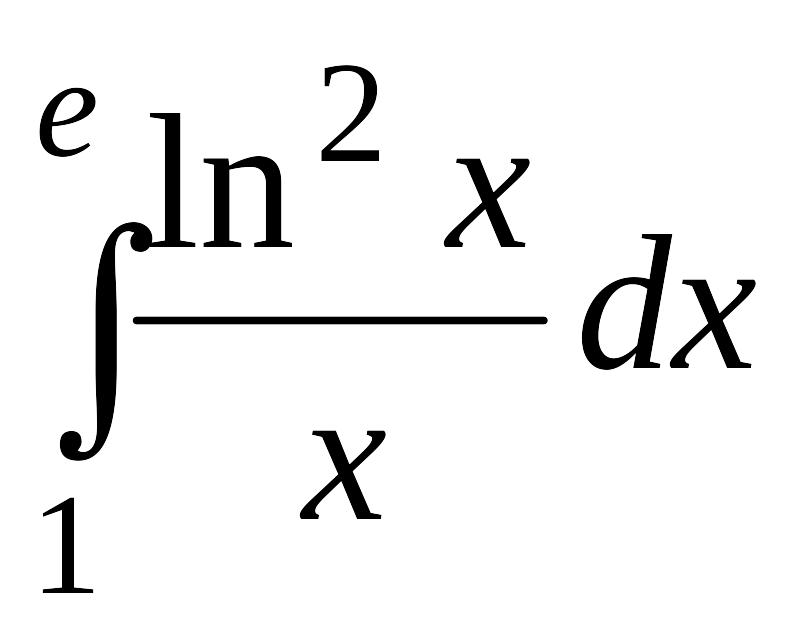 .
.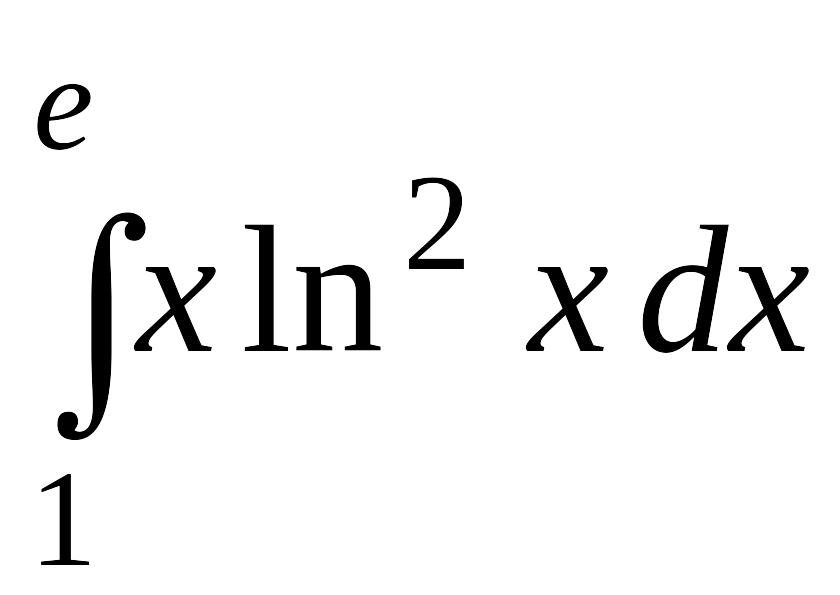 .
.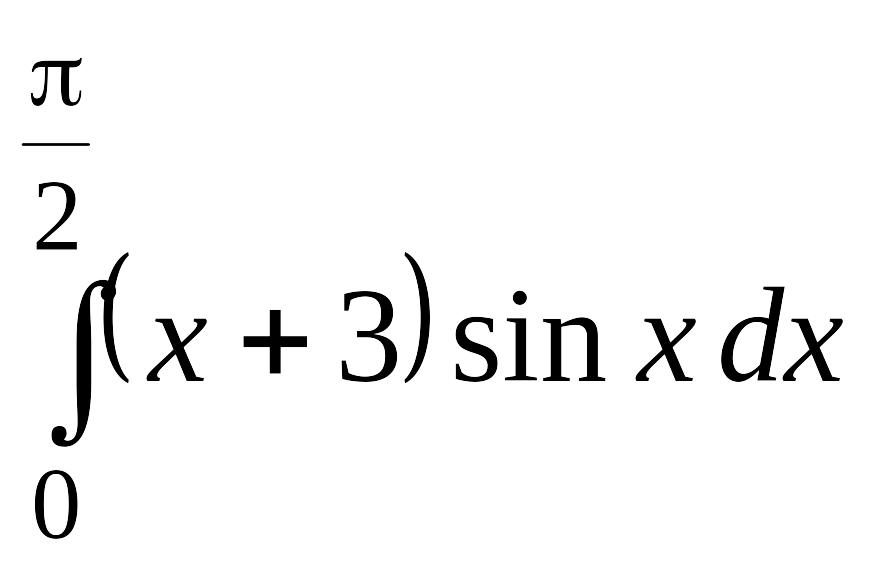 .
.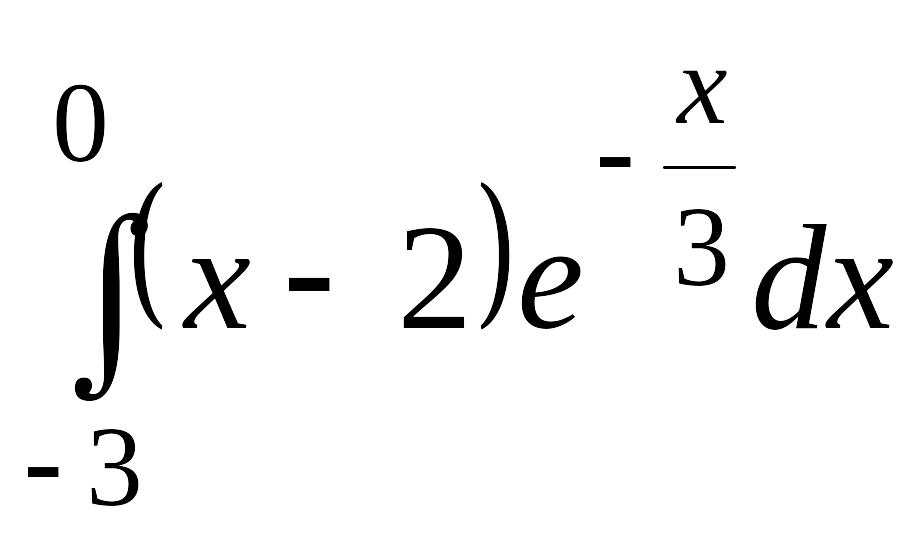 .
.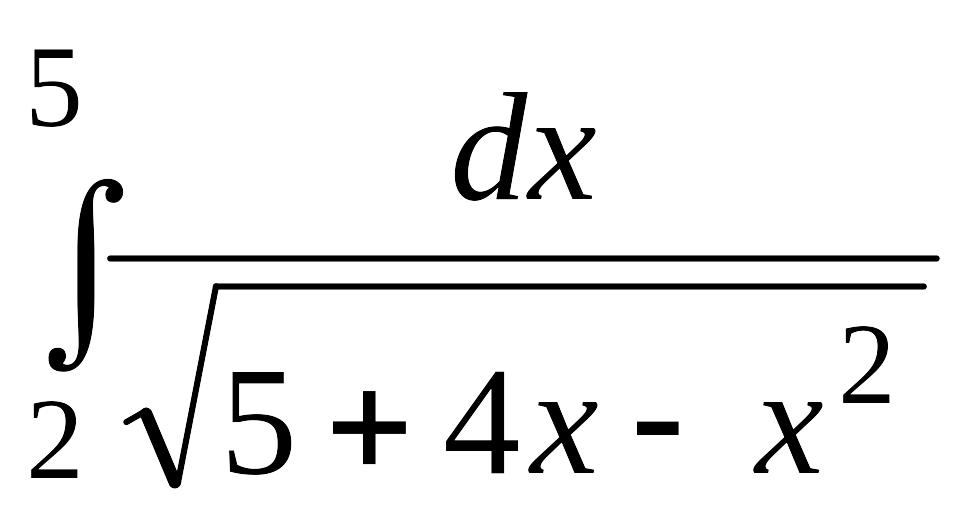 .
.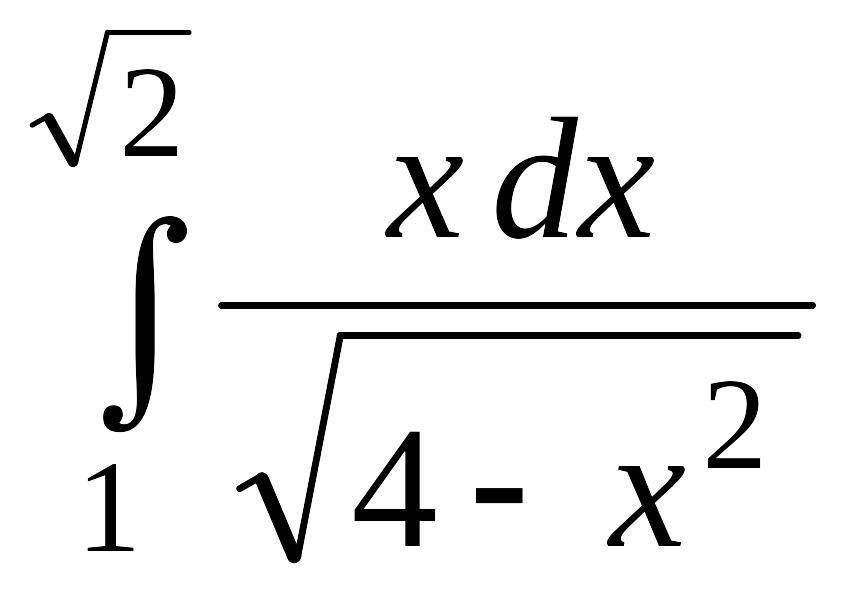 .
.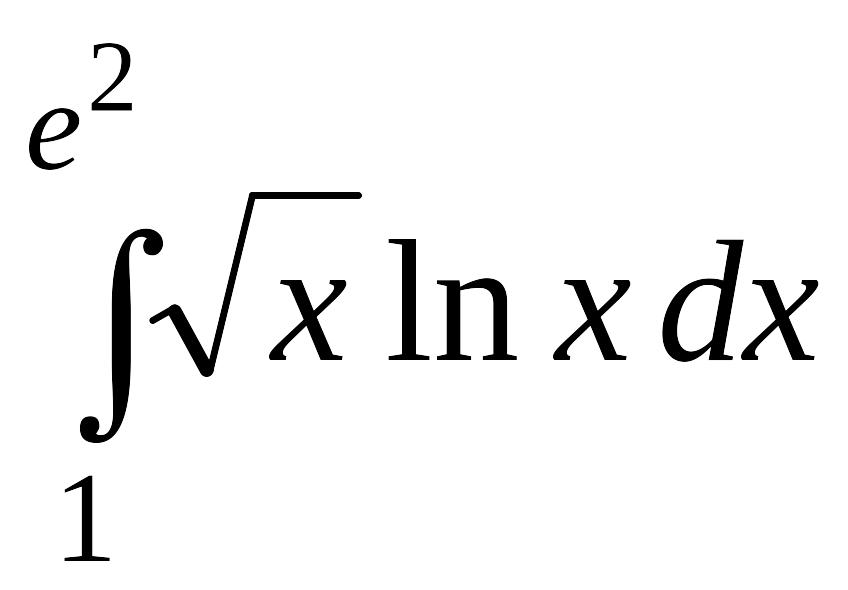 .
.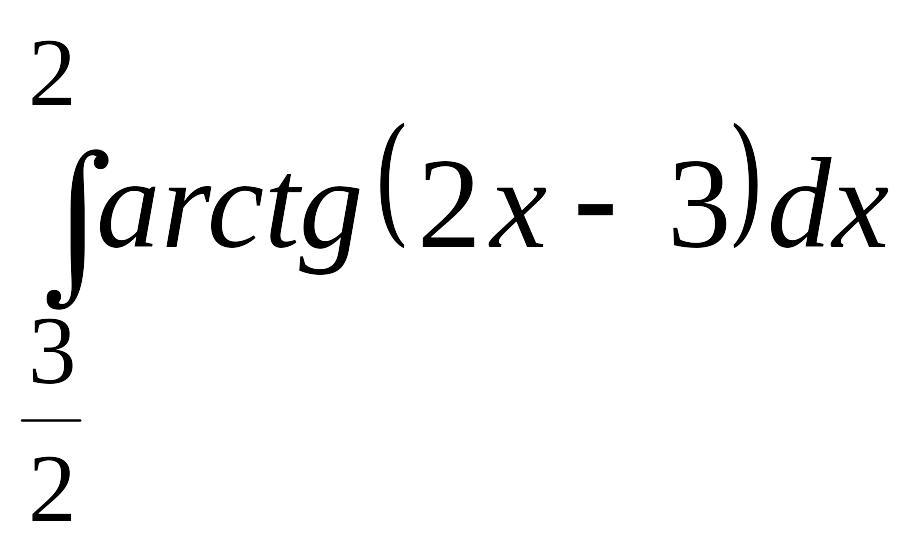 .
.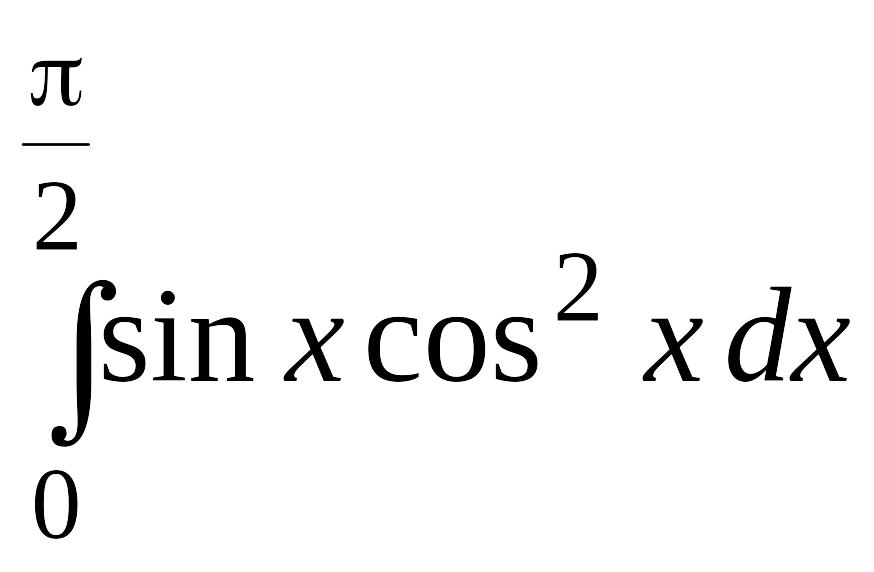 .
.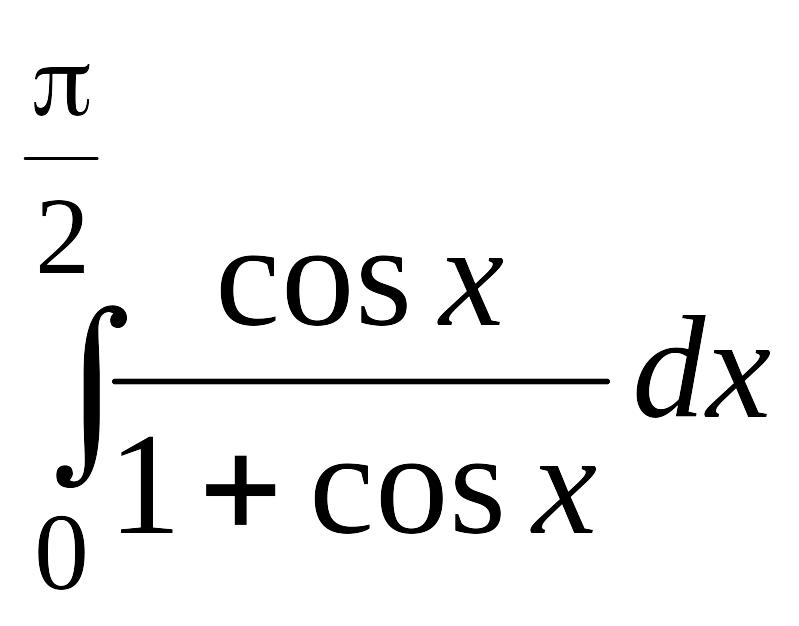 .
.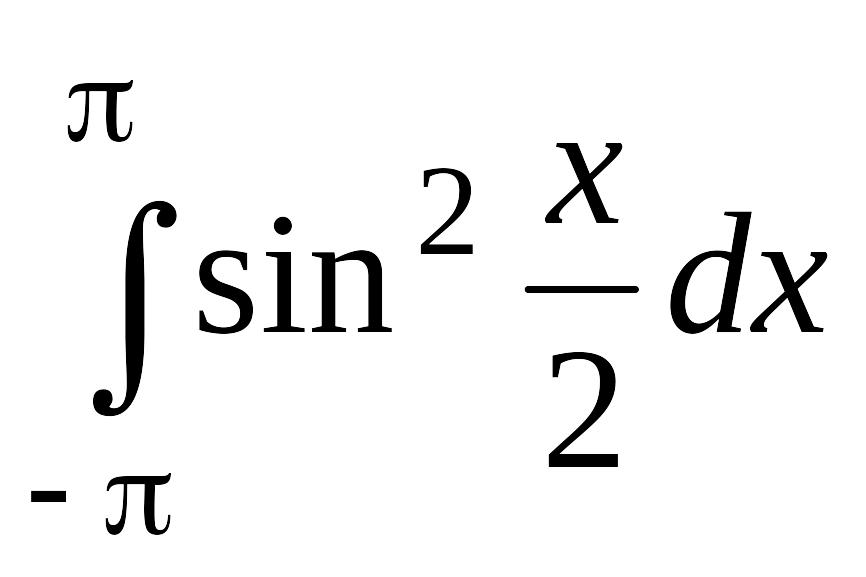 .
.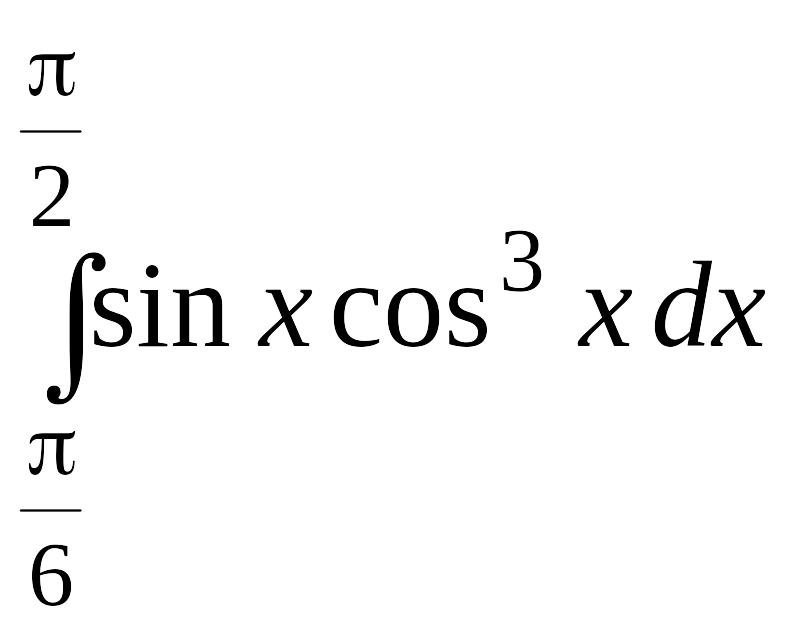 .
.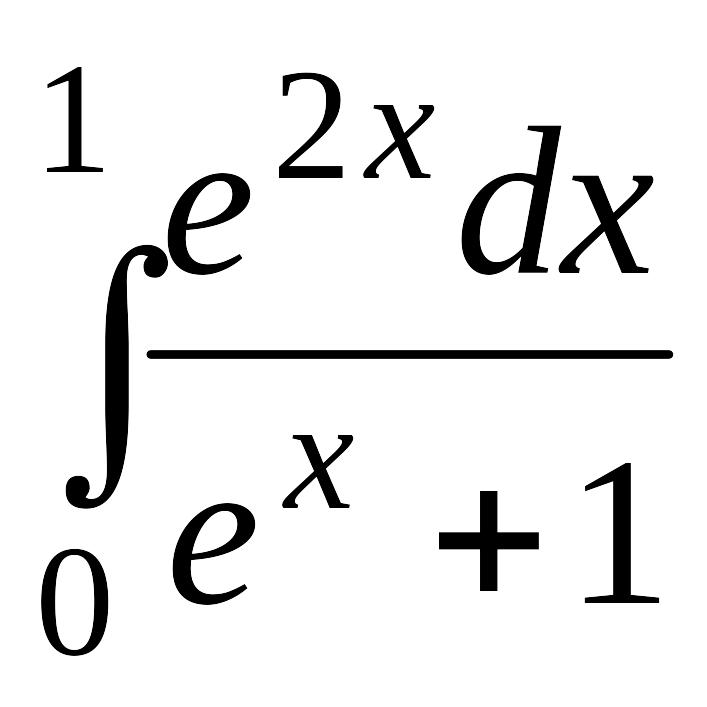 .
.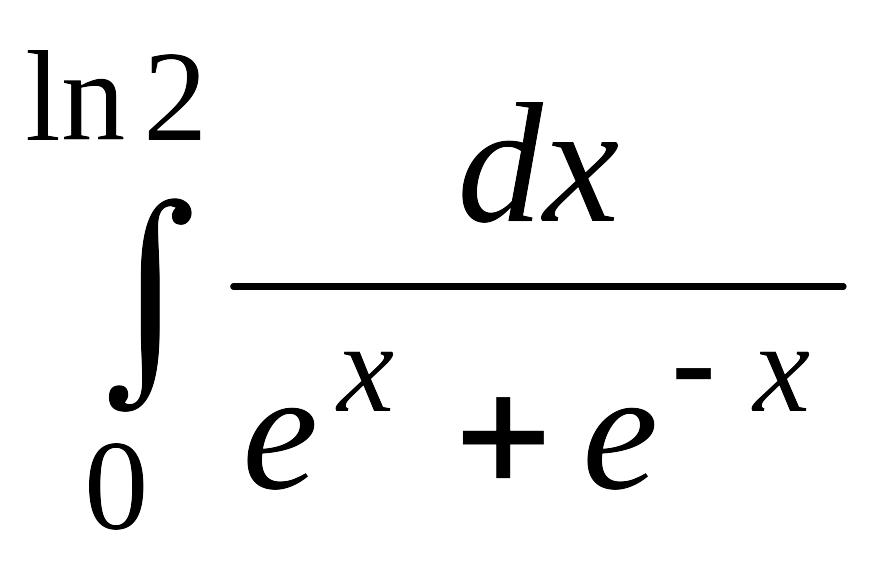 .
.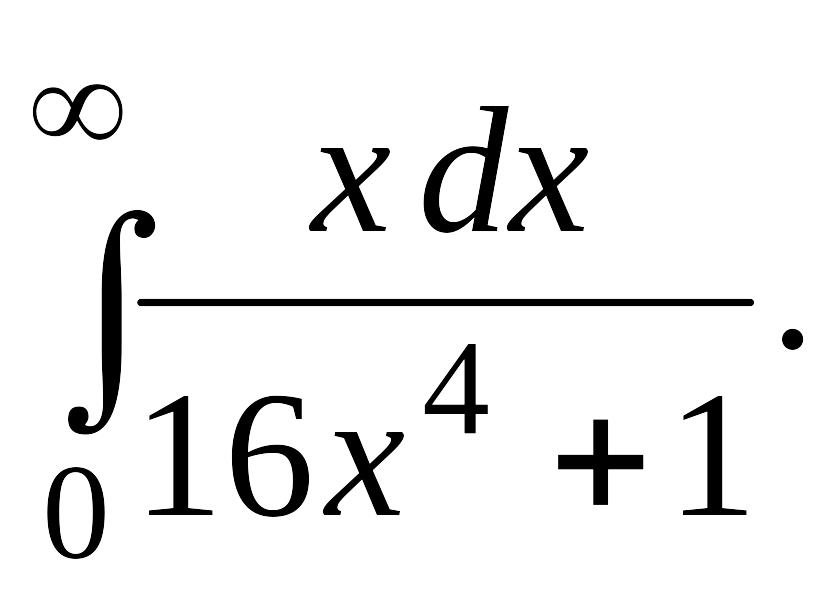
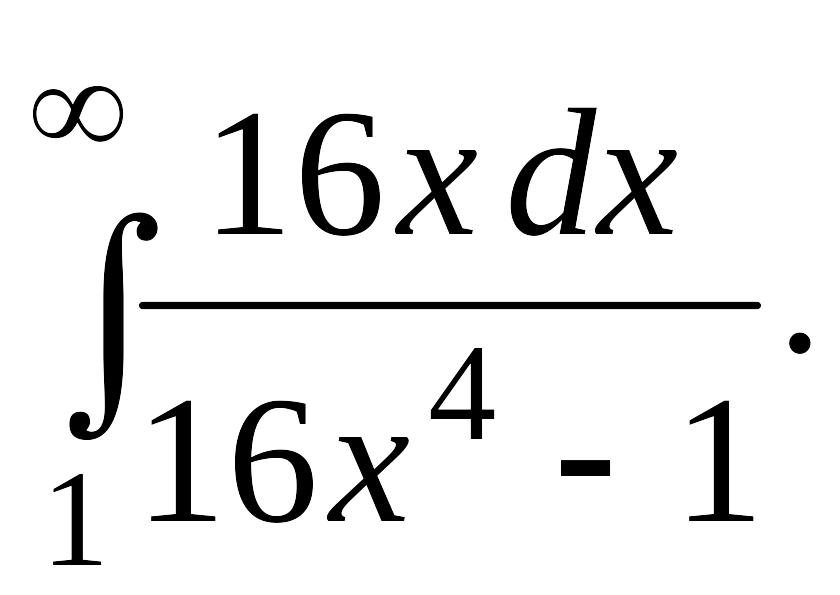
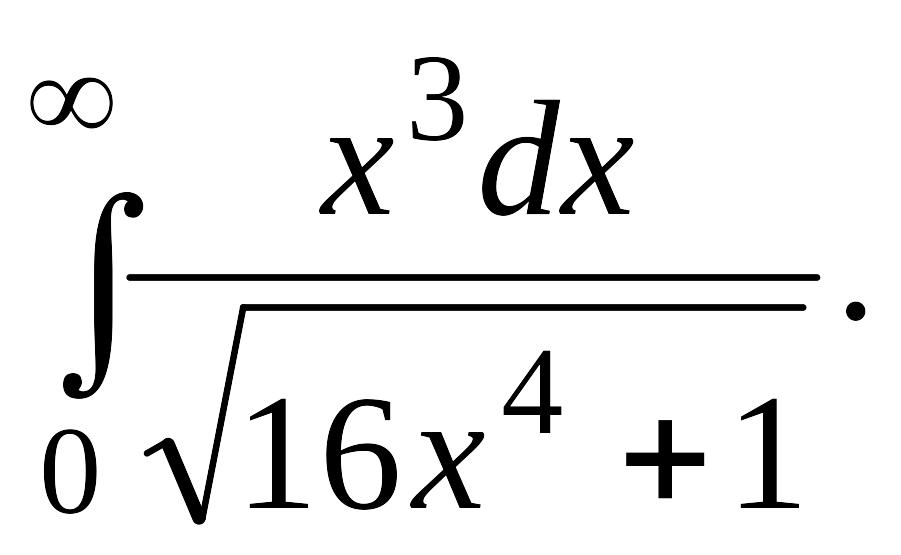
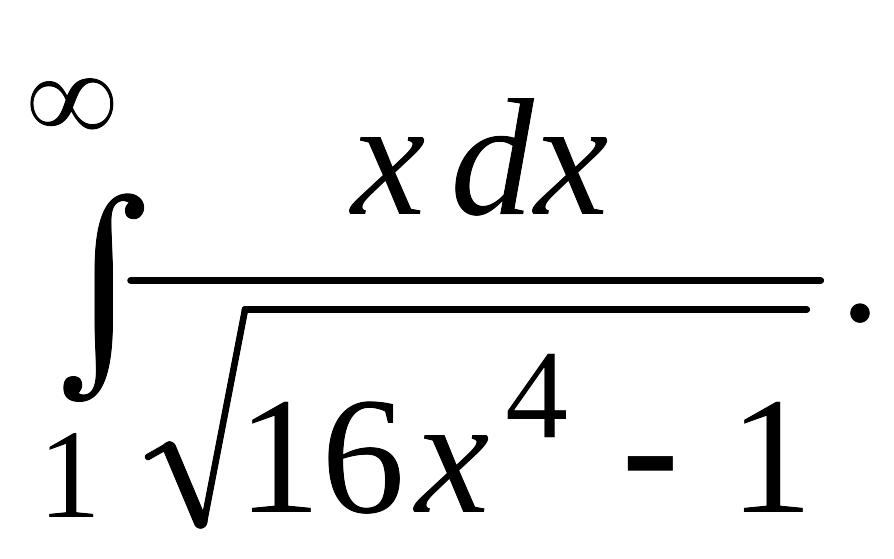
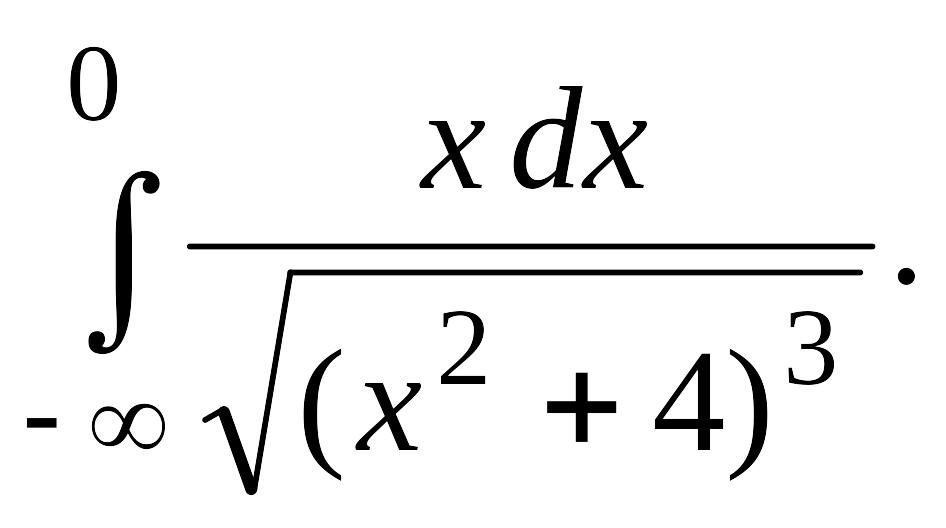
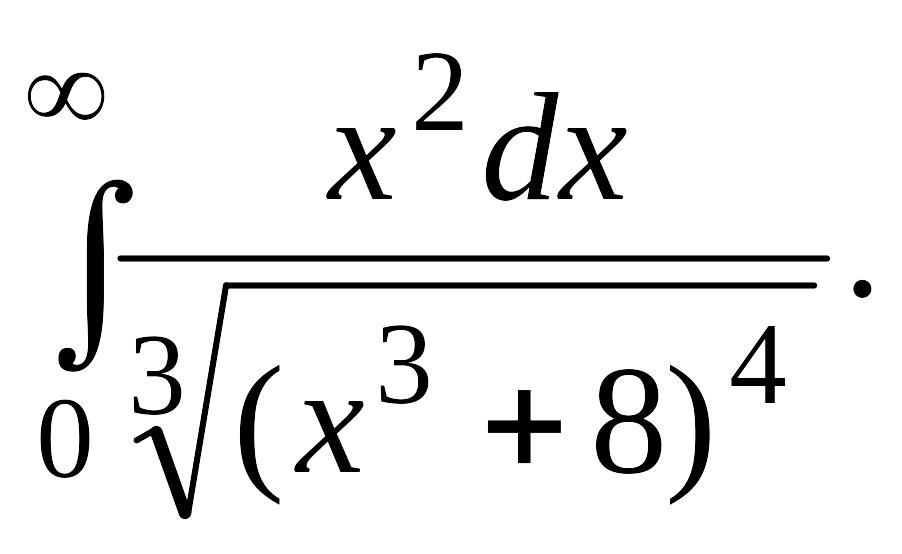
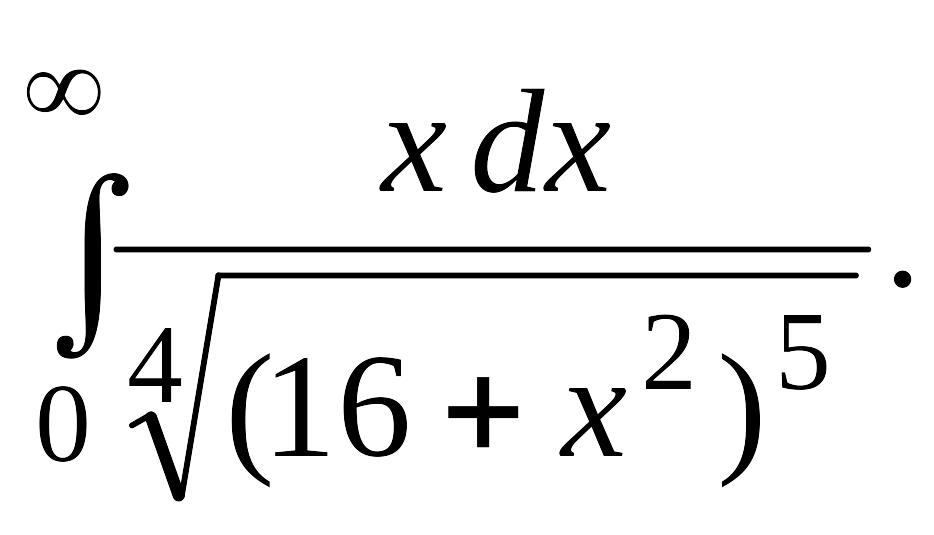
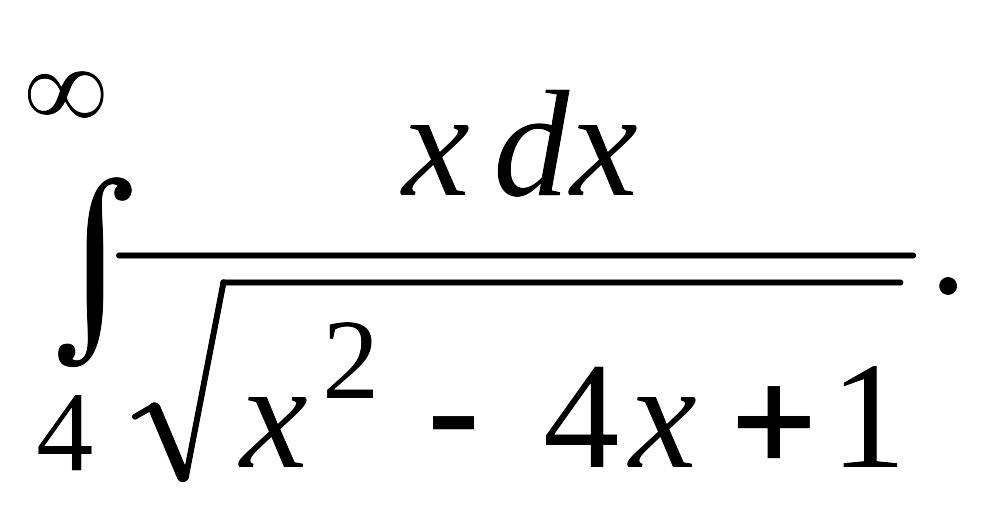
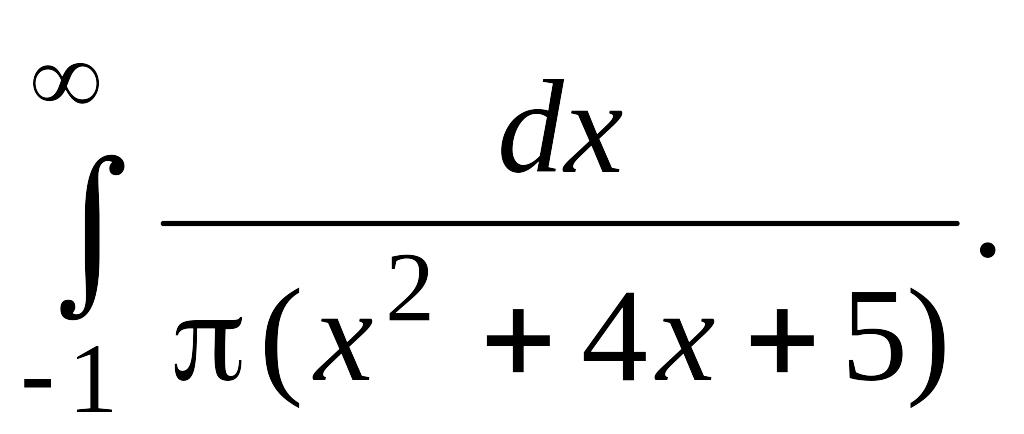
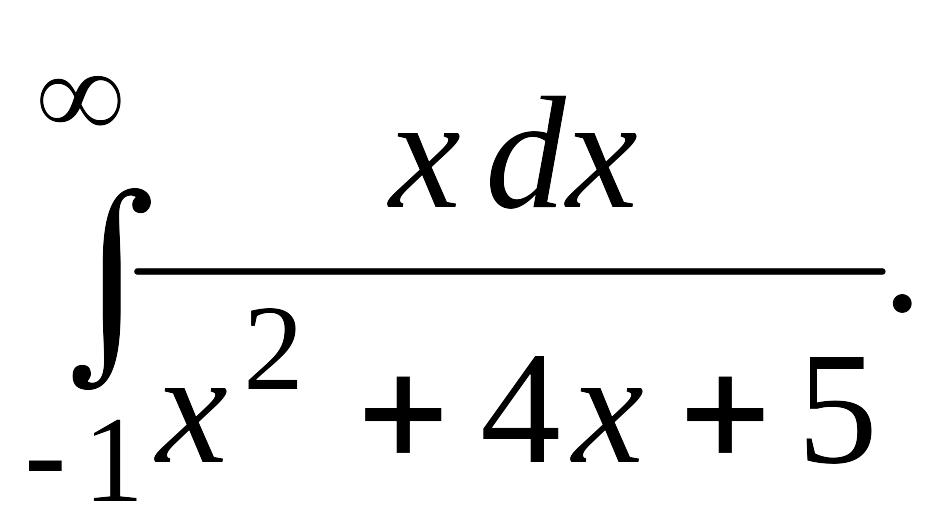
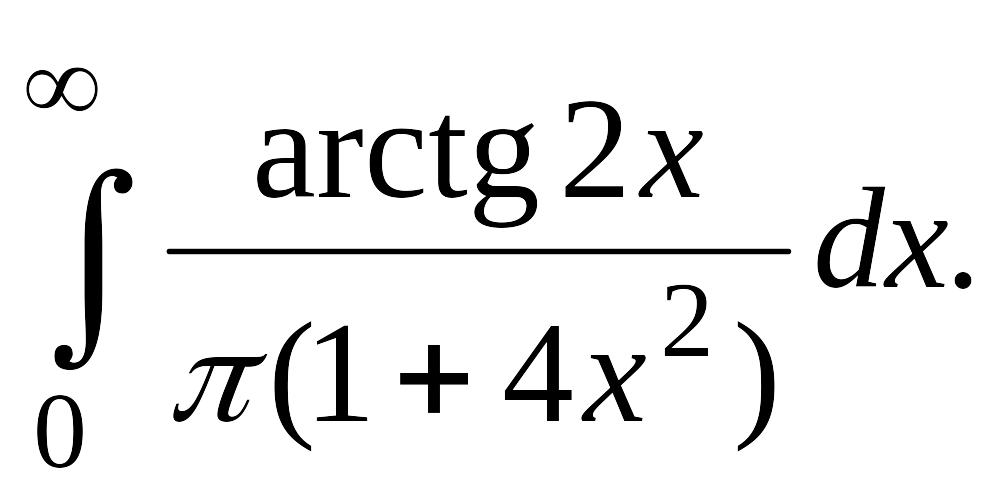
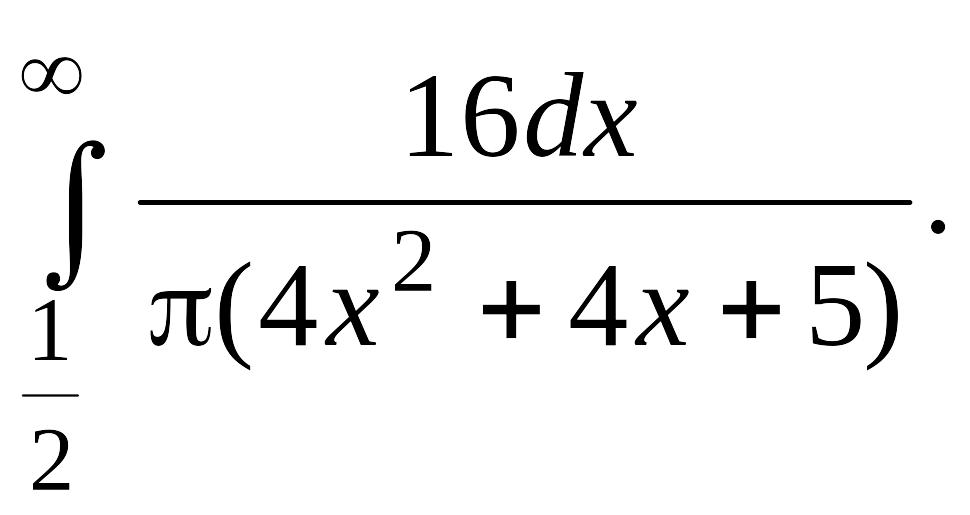
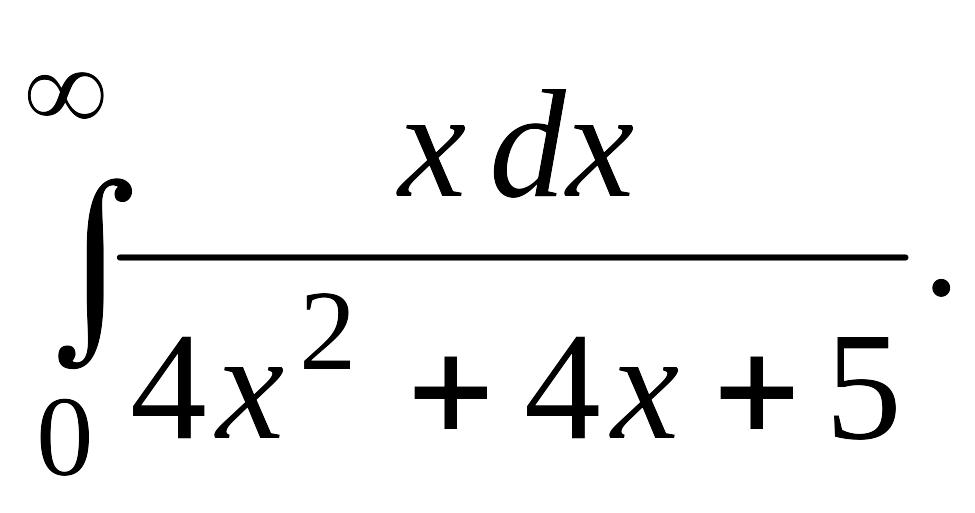
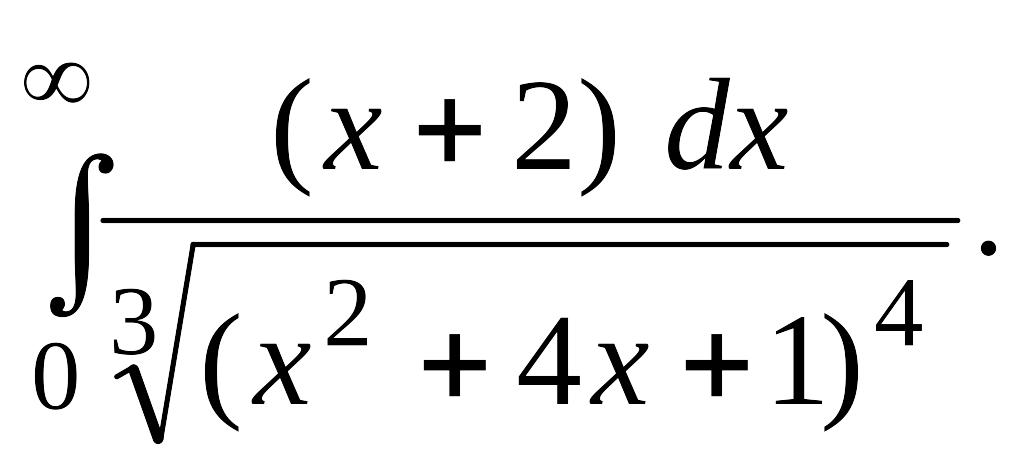
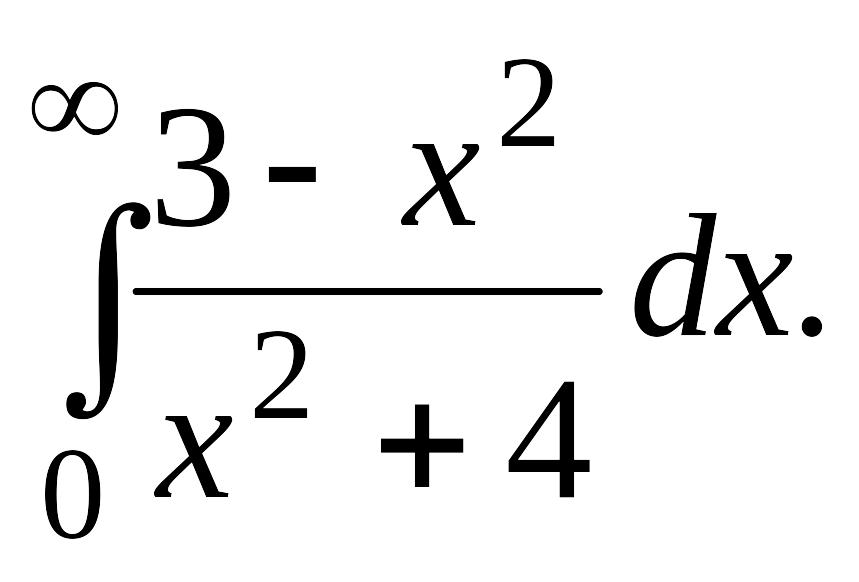
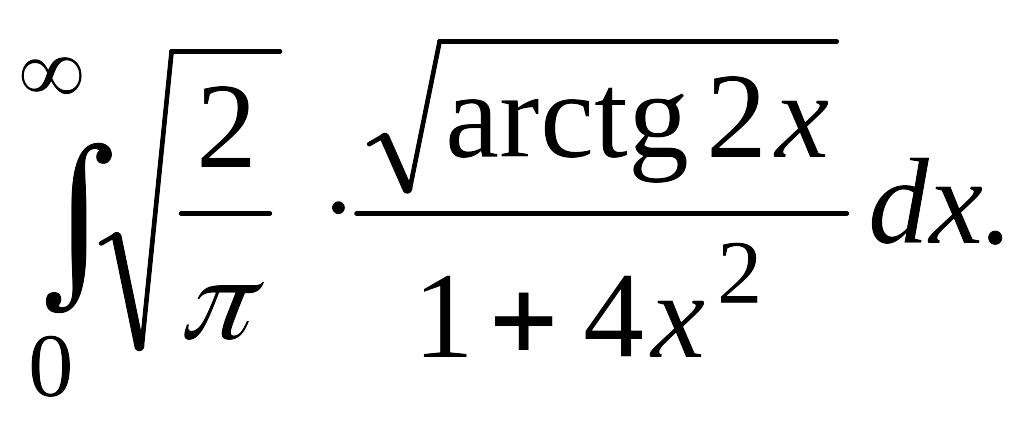
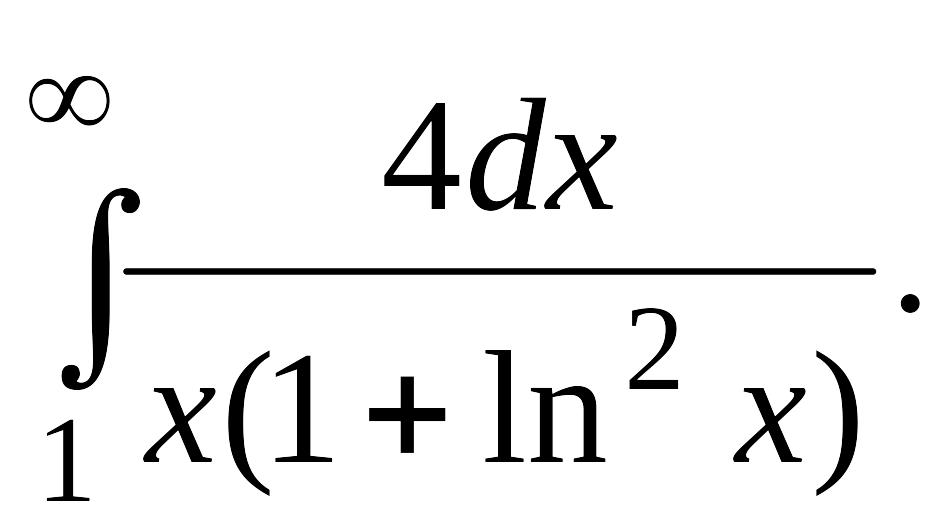
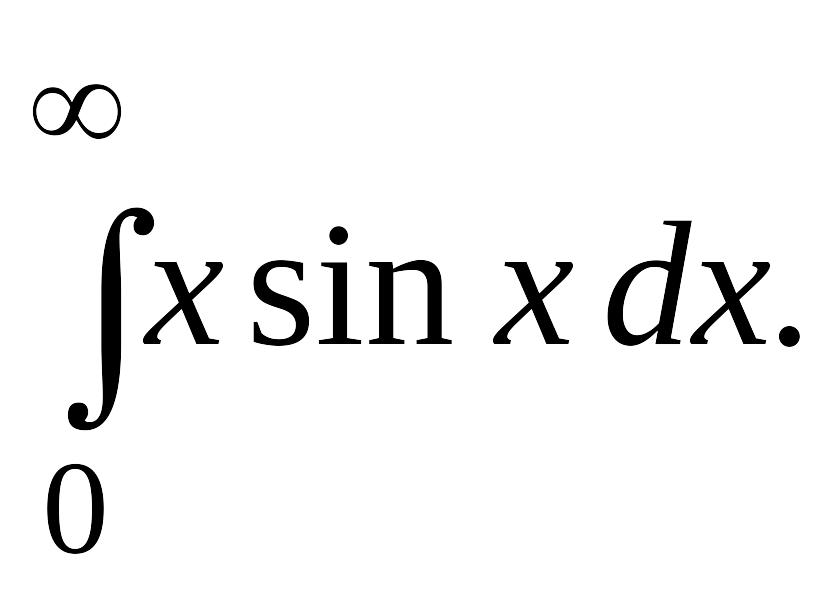
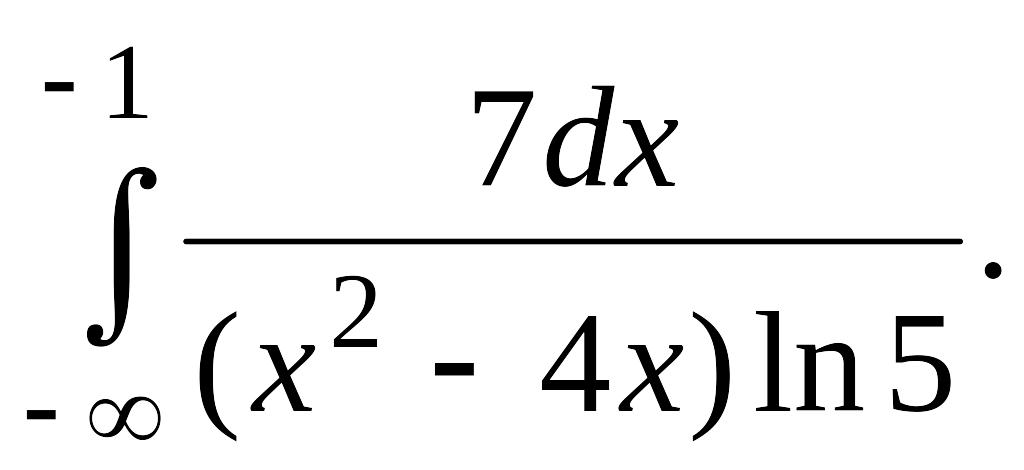
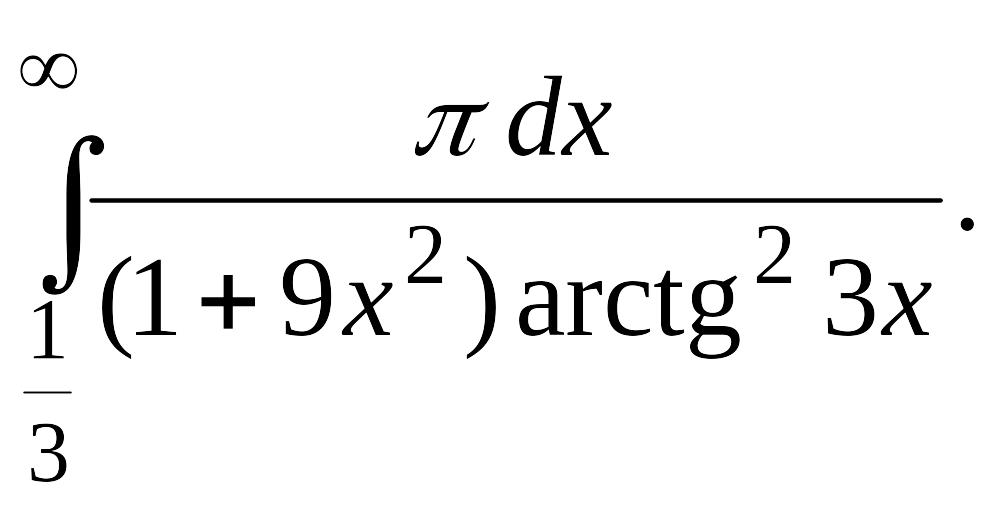
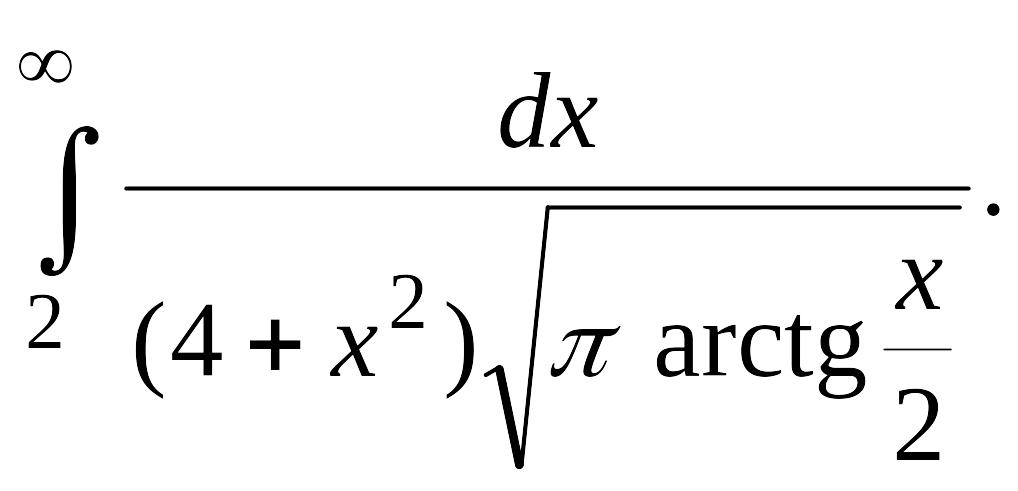
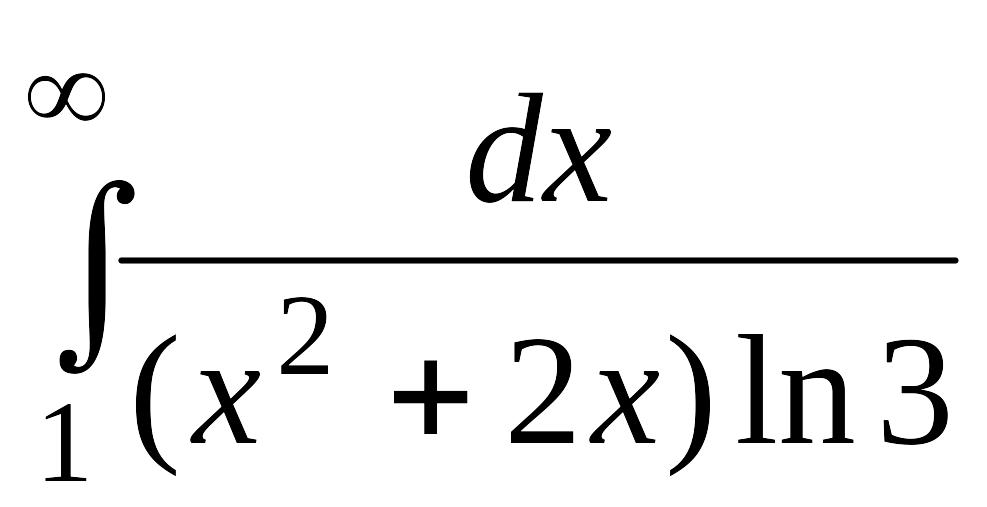 .
.