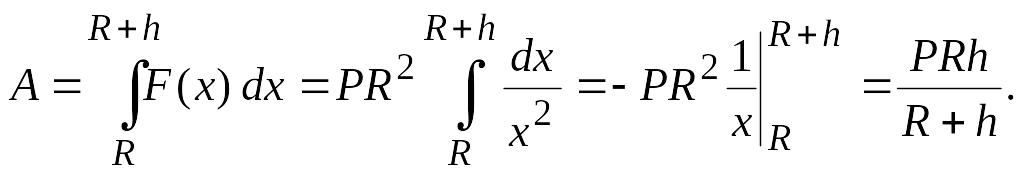Формула интегрирования по частям в определенном интеграле
Теорема. Если функции и имеют непрерывные производные на отрезке , то справедлива формула
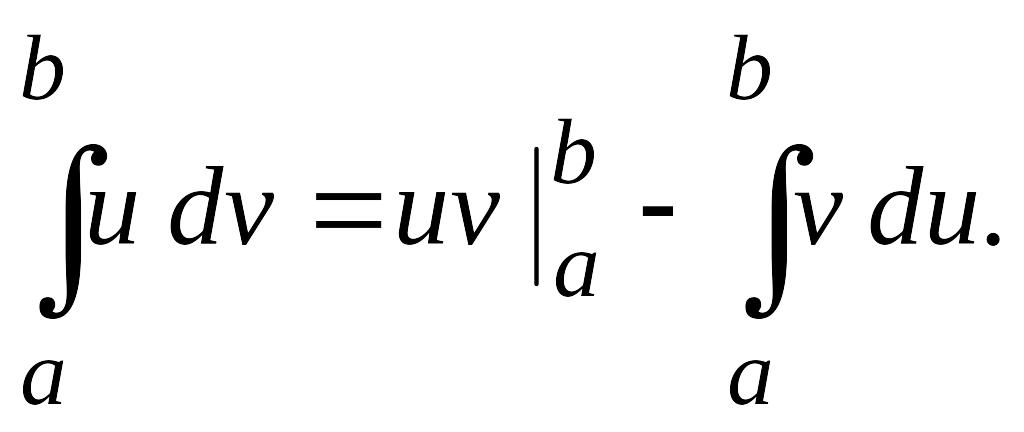(3.8)
Формула (3.8) называется формулой интегрирования по частям в определенном интеграле.
Пример 1.
Вычислить
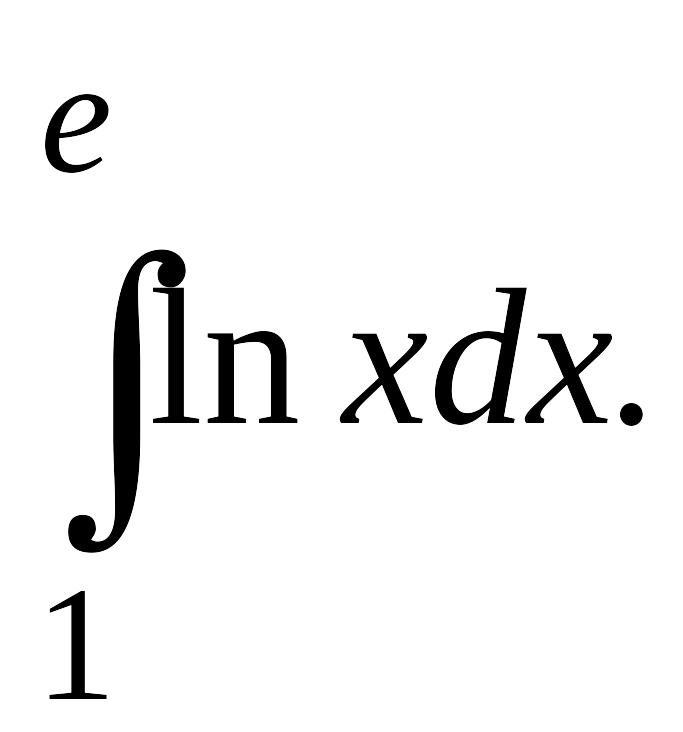
Решение.
Положим
,
;
отсюда
и по формуле (3.8) находим
.
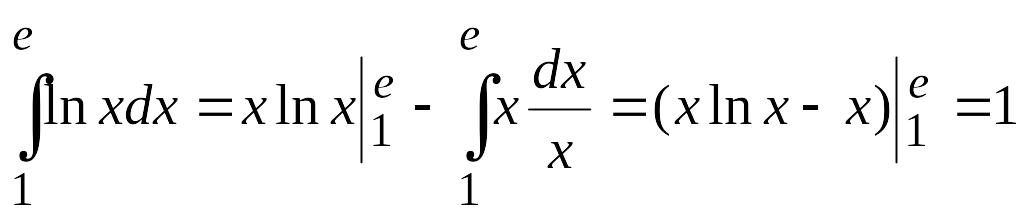Пример 2.
Вычислить
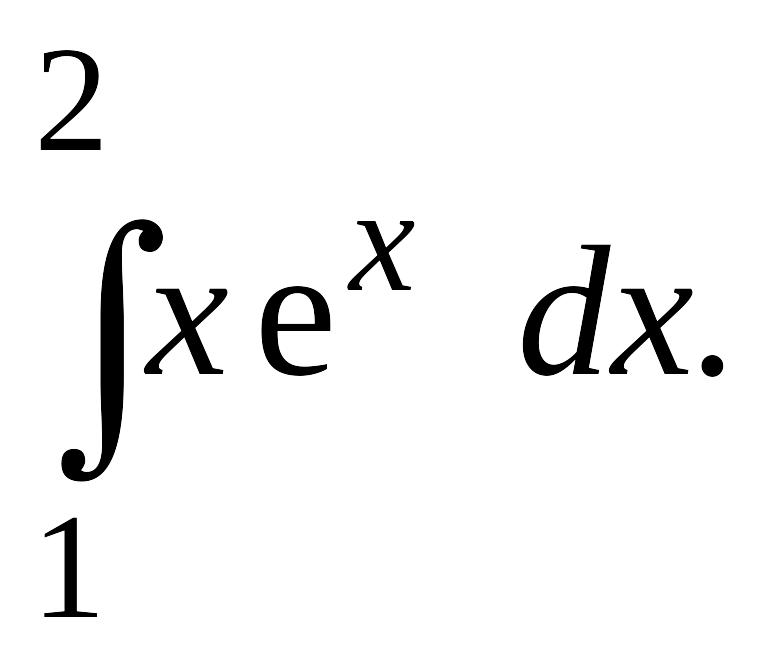
Решение.
Положим
отсюда
и по формуле (3.8) имеем
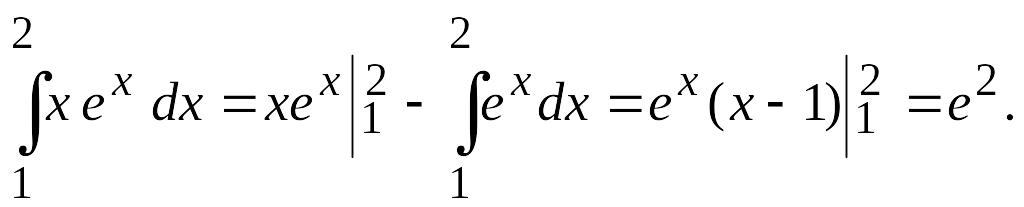
Пример 3.
Вычислить
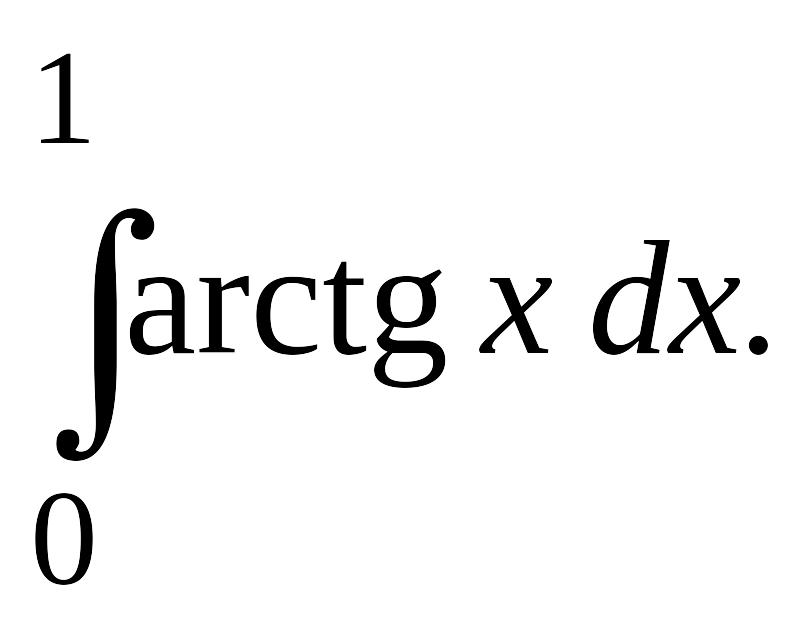
Решение.
Положим
,
;
отсюда
и по формуле (3.8) находим
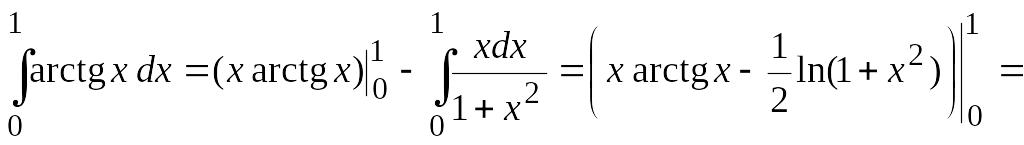
Некоторые физические и геометрические приложения определенного интеграла
1. Площадь
криволинейной трапеции. Пусть
на плоскости Oxy
дана фигура, ограниченная отрезком
оси Ох,
прямыми
,
и графиком непрерывной и неотрицательной
функции
на
.
Это криволинейная трапеция, площадь s
которой может быть вычислена по формуле
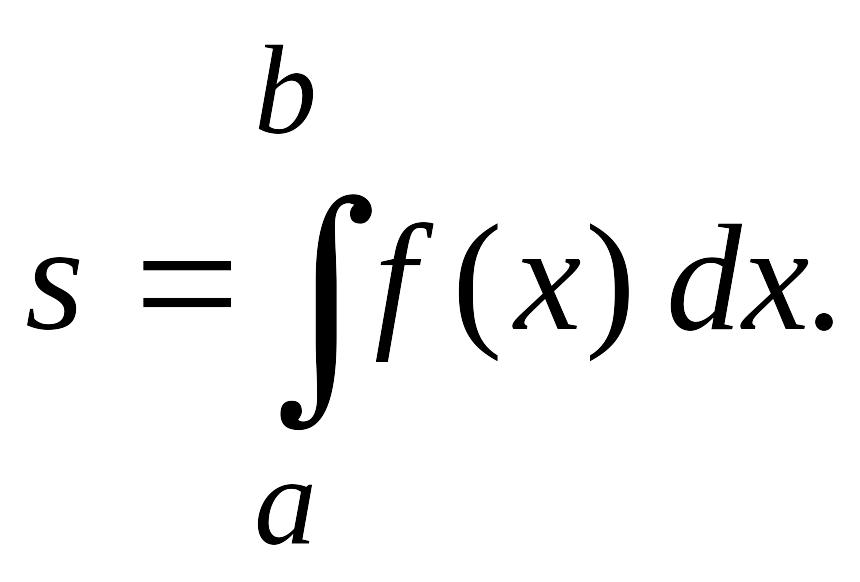(3.9)
Итак, определенный интеграл от неотрицательной непрерывной функции по численно равен площади криволинейной трапеции с основанием , ограниченной сверху графиком функции . В этом и заключается геометрический смысл определенного интеграла.
Пример 1.
Найти площадь
фигуры, ограниченной графиком функции
прямой
и осью Ох.
Решение.
По формуле (3.9) имеем
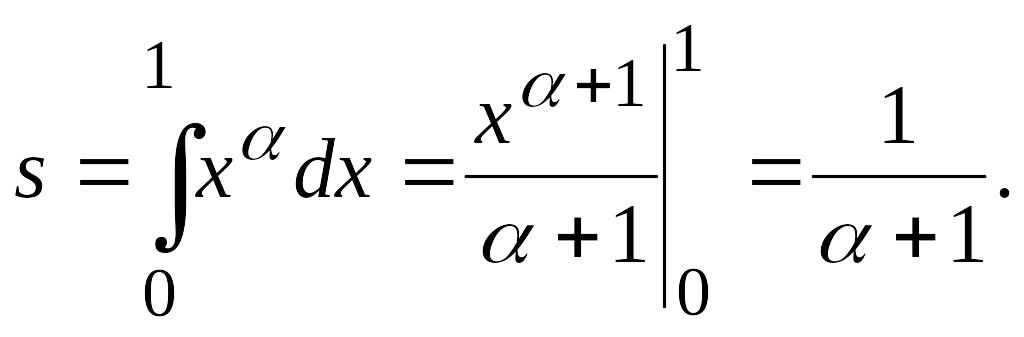
Если
,
то s
1/2; если
то s
1/3, и т. д.
Пусть фигура
ограничена снизу и сверху графиками
функций
и
(рис. 7), где
две
непрерывные функции. Если обе функции
неотрицательны, то площадь s
данной
фигуры равна разности площадей
криволинейных трапеций, ограниченных
сверху соответственно графиками функций
Следовательно,
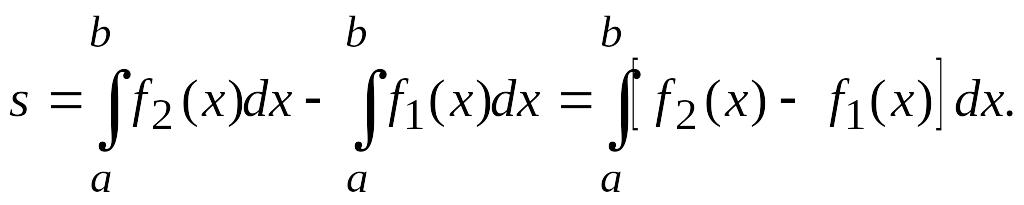(3.10)
Заметим, что формула
(3.10) справедлива и тогда, когда
и
не являются
неотрицательными.
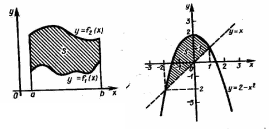
Рис. 7
Рис. 8
Пример 2. Вычислить площадь фигуры, ограниченной
графиками функций
и
(рис.
8).
Решение.
Найдем абсциссы точек пересечения
прямой
с параболой
.
Решая систему уравнений
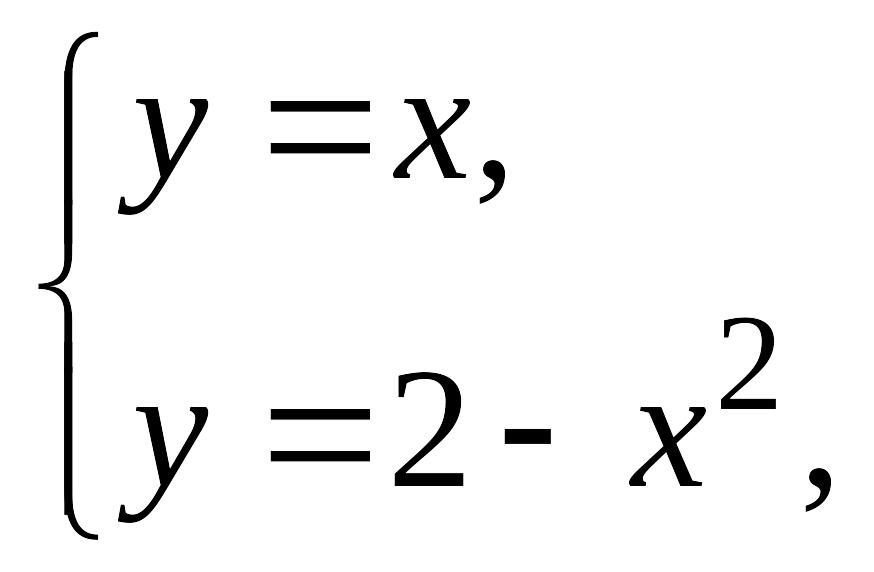получаем
Это и есть пределы интегрирования.
Искомая площадь фигуры согласно формуле
(3.10) такова:
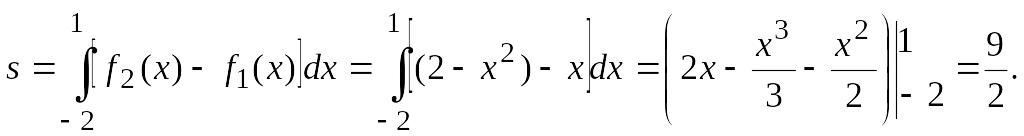
З а м е ч а н и е.
Для вычисления площади криволинейной
трапеции в случае, когда верхняя граница
задана параметрически уравнениями
причем
,
,
в формуле (3.9) надо сделать замену
переменной, положив
.
Тогда получим
.
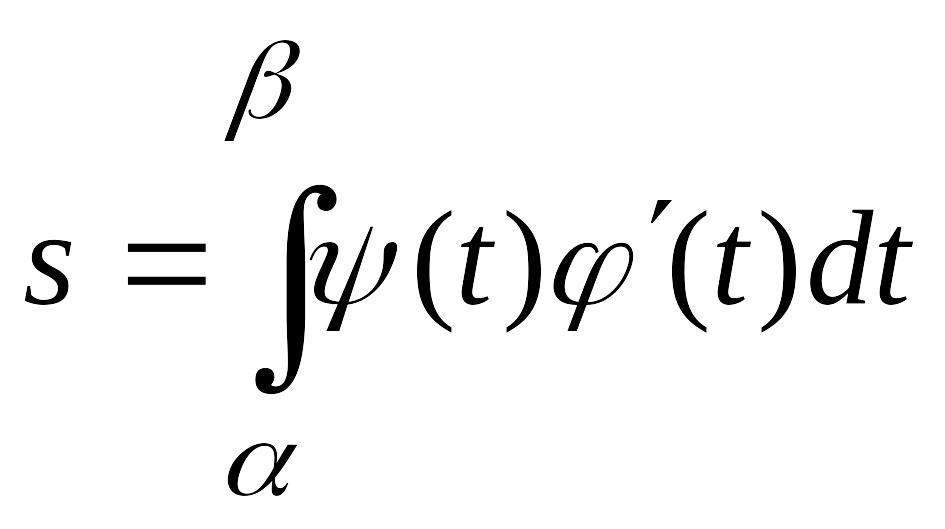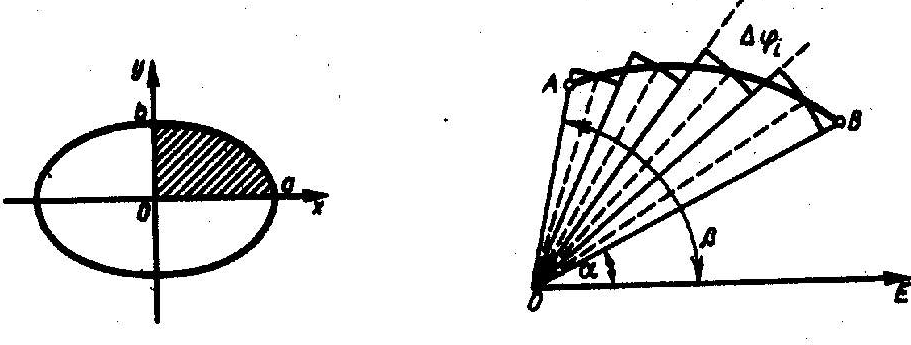
Рис. 9 Рис. 10
Пример 3. Вычислить площадь фигуры, ограниченной эллипсом
Решение. Эллипс симметричен относительно осей координат, поэтому достаточно вычислить площадь части фигуры, находящейся в I четверти (рис. 9). Следовательно, искомая площадь равна
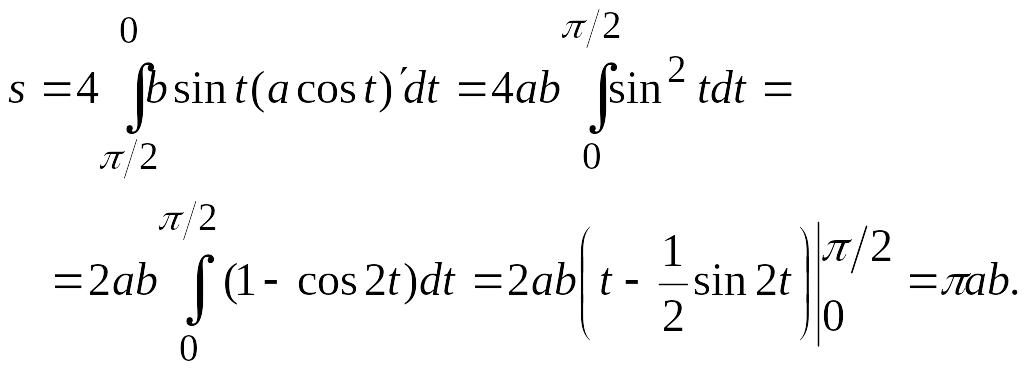
В частности, если
,
то получаем известную формулу площади
круга
2. Площадь
криволинейного сектора. Пусть
кривая АВ
задана в полярных координатах уравнением
причем функция
непрерывна и неотрицательна на отрезке
.
Плоскую фигуру, ограниченную кривой АВ
и двумя лучами, составляющими с полярной
осью углы
и
будем называть криволинейным
сектором
(рис. 10). Площадь
криволинейного сектора находится по
формуле
.
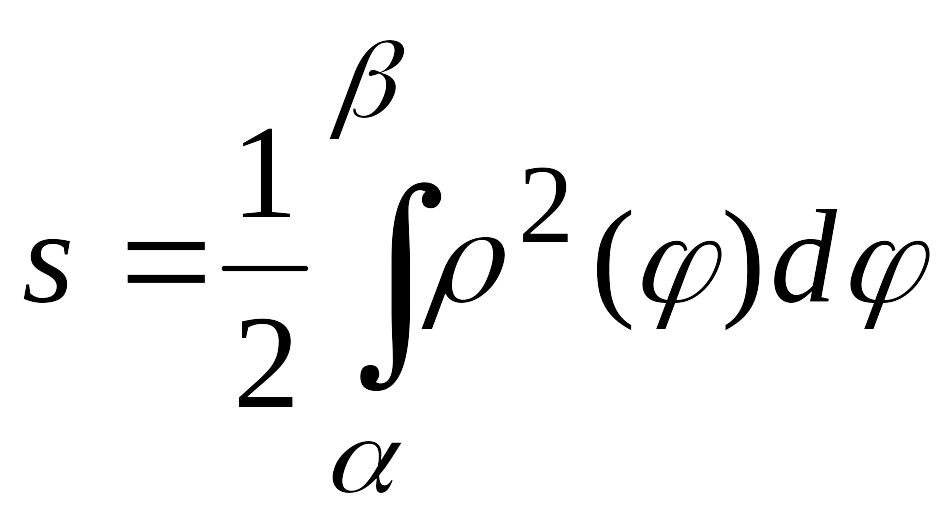(3.11)
Пример 4.
Вычислить
площадь фигуры, ограниченной полярной
осью и первым витком спирали Архимеда:
где а
– положительное число (рис. 11).
Решение.
При изменении
от 0 до
полярный радиус описывает кривую,
ограничивающую криволинейный сектор
ОАВС.
Поэтому по формуле (3.11) имеем
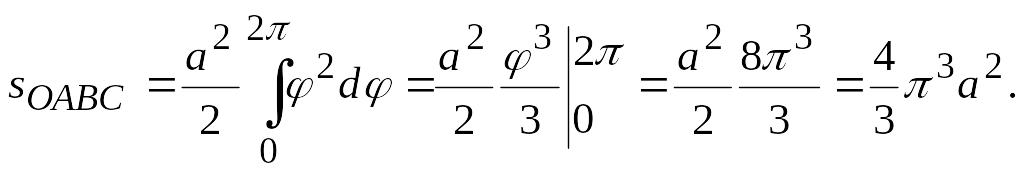
Расстояние от
точки С
до полюса равно
.
Поэтому круг радиуса ОС
имеет площадь
т. е. площадь фигуры, ограниченной
полярной осью и первым витком спирали
Архимеда, равна
площади круга с радиусом, равным
наибольшему из полярных радиусов витка.
К этому выводу пришел Архимед.
Рис. 11 Рис. 12
3. Длина дуги
кривой.
Пусть плоская кривая AB
задана
уравнением
,
где
– непрерывная функция на отрезке
.
Разобьем кривую АВ
на n
произвольных частей точками
в направлении от А
к В.
Соединив соседние точки хордами, получим
некоторую вписанную в кривую АВ
ломаную, длину которой обозначим через
Р
(рис. 12).
Через
обозначим
длину одного звена
ломаной, а через
длину
наибольшего из звеньев:
Определение.
Число L
называется пределом длин ломаных P при
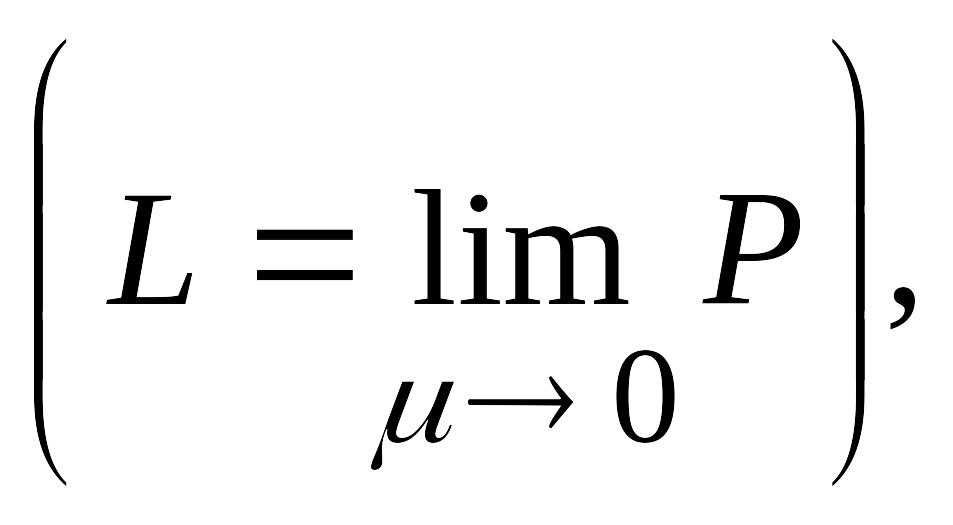если для любого
существует
такое, что для всякой ломаной,
у которой
,
выполняется
неравенство
Если существует
предел L
длин P
вписанных в кривую ломаных при
то этот предел называется длиной
дуги АВ.
Если функция
непрерывна вместе с
на отрезке
,
то длина дуги АВ
выражается
формулой
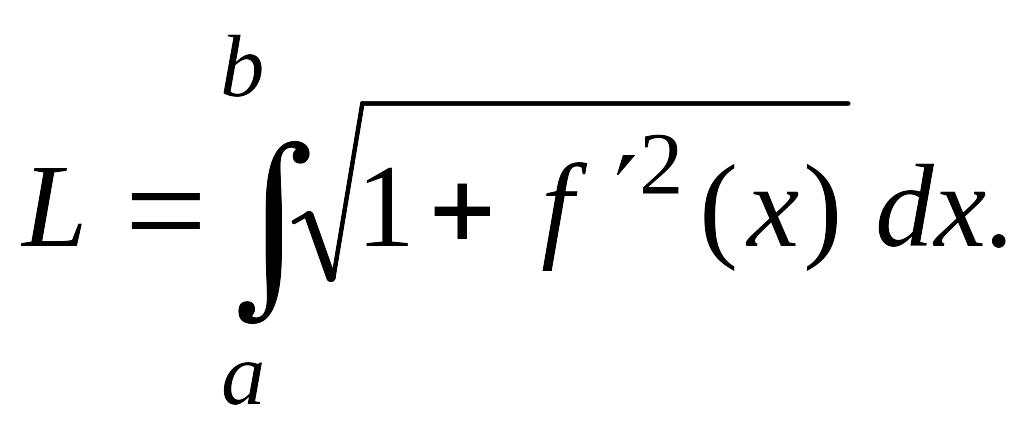(3.12)
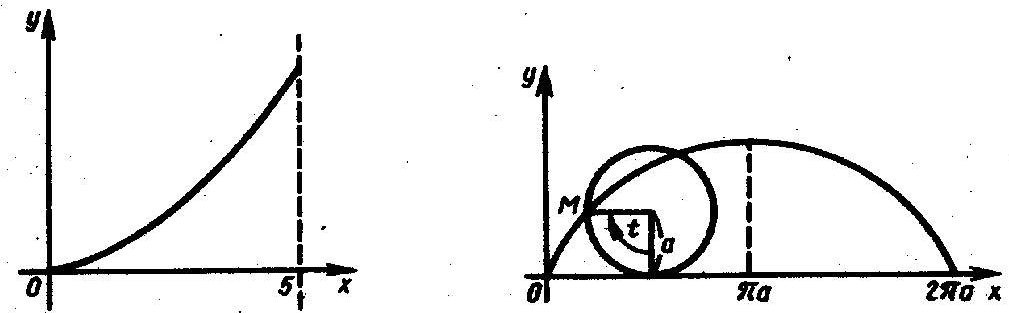
Рис. 13 Рис. 14
Пример 5.
Вычислить
длину дуги верхней ветви полукубической
параболы
если
(рис. 13).
Решение.
Из уравнения
находим:
Следовательно, по формуле (3.12) получим
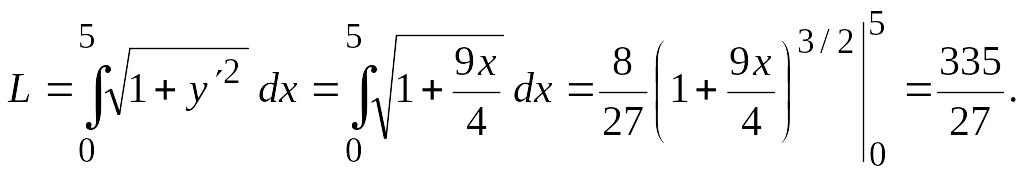
З а м е ч а н и е 1.
Для вычисления длины дуги в случае,
когда кривая AB
задана параметрически уравнениями
,
где
и
значения
параметра t,
соответствующие значениям
,
,
т.е.
в формуле
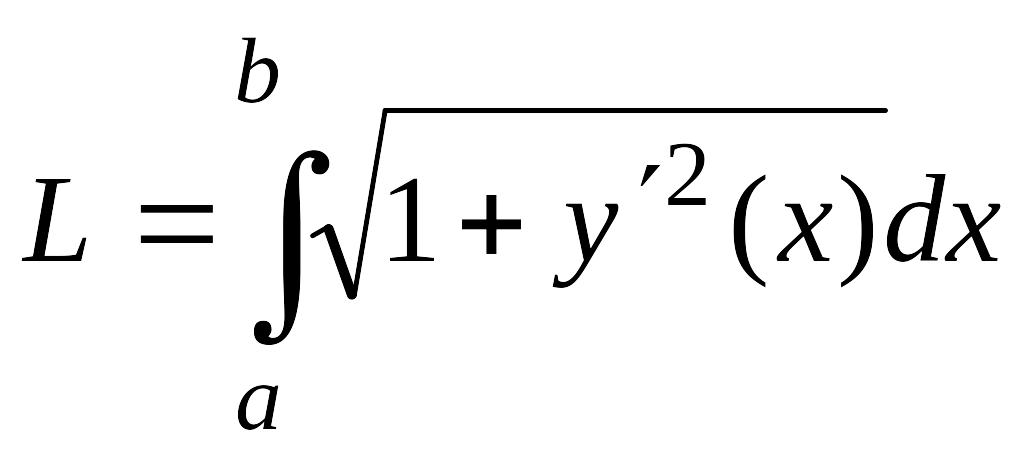надо сделать замену переменной, положив
Тогда получим
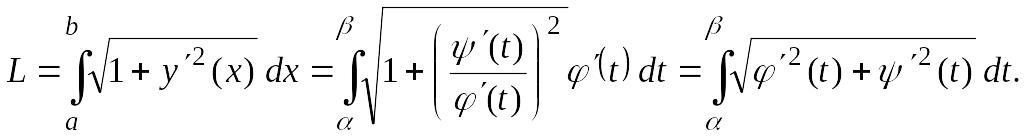(3.13)
Пример 6.
Вычислить длину дуги одной арки циклоиды:
(рис. 14).
Решение.
Из уравнений циклоиды находим:
Когда х
пробегает отрезок
параметр t
пробегает
отрезок
Следовательно, искомая длина дуги равна
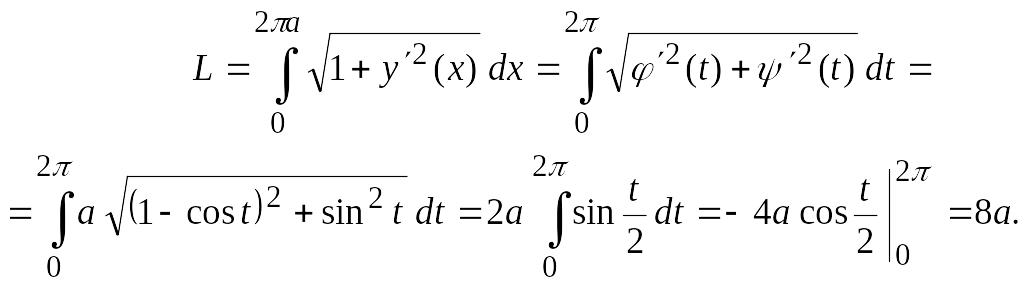
З а м е ч а н и е 2.
Для вычисления длины дуги в случае,
когда кривая AB
задана в
полярных координатах уравнением
где
имеет непрерывную производную
на отрезке
,
и точкам A
и B соответствуют
значения
,
равные
и
,
нужно перейти от полярных координат к
прямоугольным. Тогда получим параметрическое
задание кривой AB
уравнениями
.
Так как
то формула (3.13) принимает вид
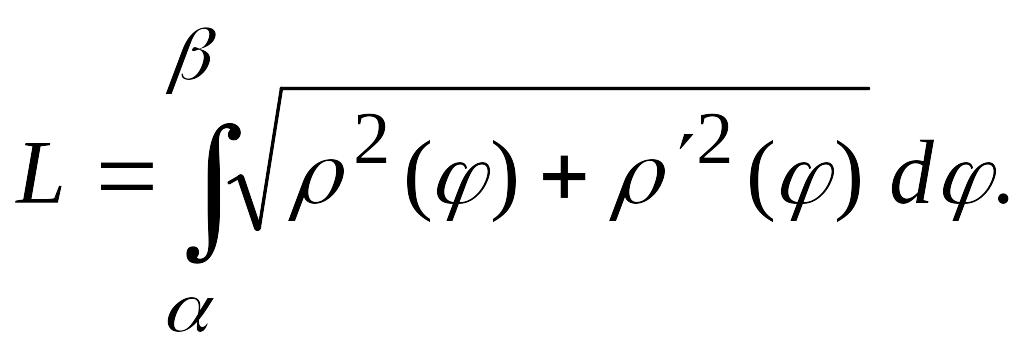(3.14)
Пример 7.
Вычислить длину первого витка спирали
Архимеда:
(см. рис. 11).
Решение. Первый виток спирали образуется при изменении полярного угла от 0 до . Поэтому по формуле (3.14) искомая длина дуги равна
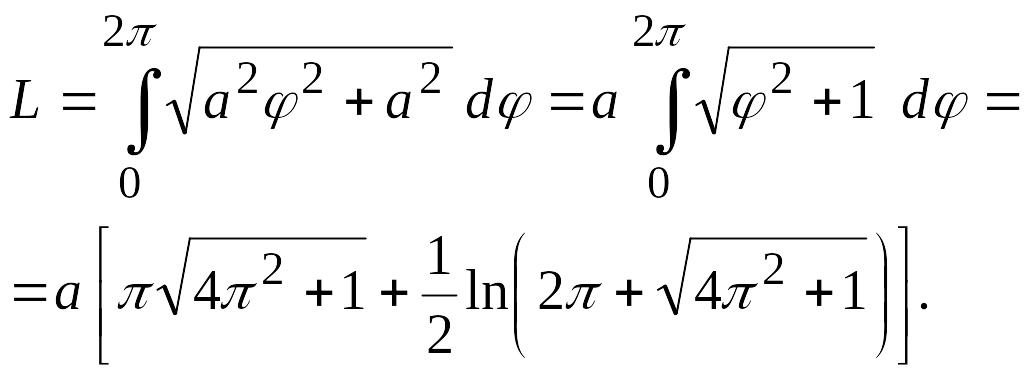
4. Объем тела вращения. Пусть функция непрерывна и неотрицательна на отрезке . Тогда тело, которое образуется вращением вокруг оси Ох криволинейной трапеции, ограниченной сверху графиком функции , (рис. 15) имеет объем
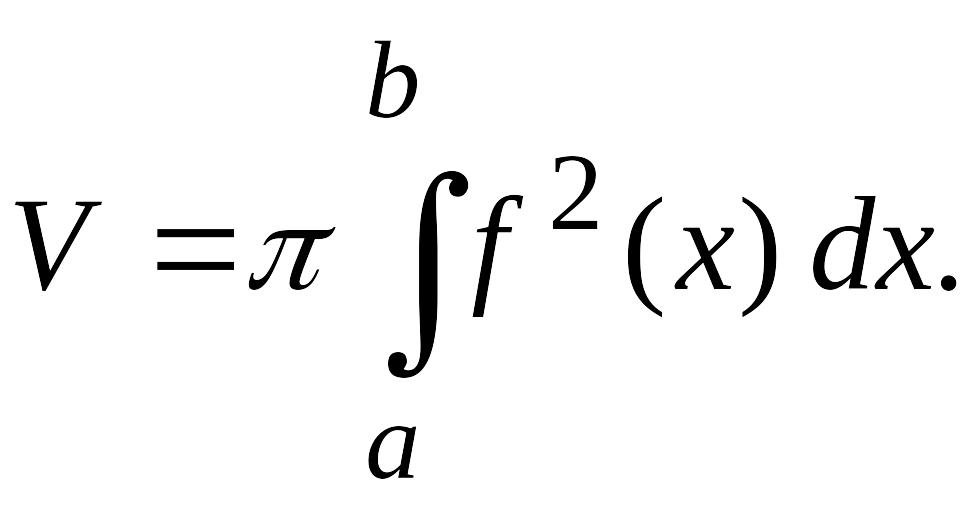
(3.15)
Рис. 15 Рис. 16
Пример 8.
Вычислить объем тора. Тором называется
тело, получающееся при вращении круга
радиуса a
вокруг оси, лежащей в его плоскости на
расстоянии b
от центра
круга
.
Форму тора имеет, например, баранка.
Решение. Пусть круг вращается оси Ох (рис. 16). Объем тора можно представить как разность объемов тел, полученных от вращения криволинейных трапеций ABCDE и ABLDE вокруг оси Ох.
Уравнение окружности
LBCD
имеет вид
причем уравнение кривой BCD
а уравнение кривой BLD
Используя формулу
(3.15), получаем для объема
тора выражение
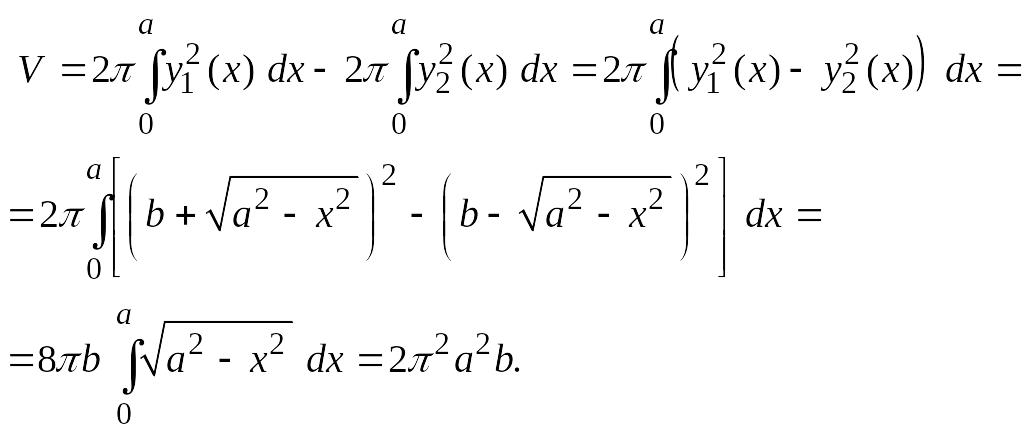
5. Площадь поверхности вращения. Пусть функция неотрицательна и непрерывна вместе со своей первой производной на отрезке . Тогда поверхность, образованная вращением графика этой функции вокруг оси Ох, имеет площадь Р, которая может быть вычислена по формуле
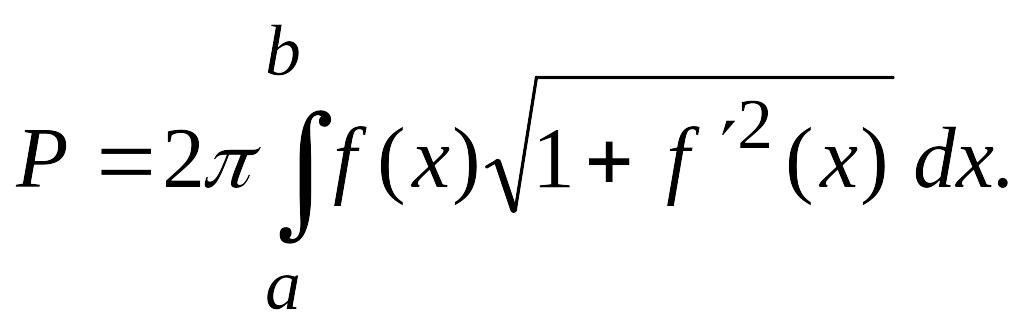(3.16)
З а м е ч а н и е.
Если поверхность получается вращением
вокруг оси Ох
кривой АВ,
заданной параметрически уравнениями
причем
изменяется от a
до b
при изменении t
от
до
,
то производя в интеграле (3.16) замену
переменной
получаем
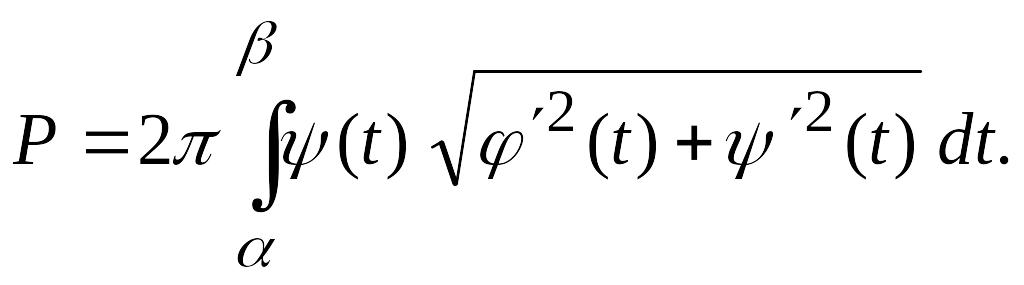(3.17)
Наконец, если
кривая задана уравнением в полярных
координатах:
где
имеет непрерывную производную на
,
то этот случай, как уже отмечалось в п.
3, сводится к параметрическому заданию
кривой
и формула (3.17) принимает вид
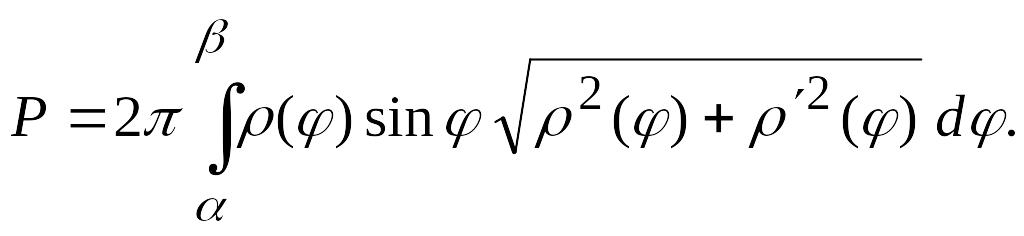
Пример 9.
Вычислить площадь P
поверхности шарового пояса, образованного
вращением полуокружности
вокруг оси Ох.
Решение. По формуле (3.16) получаем
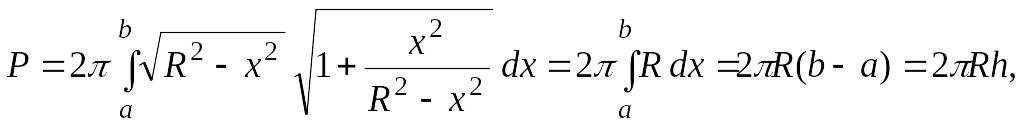где
h
– высота пояса.
Пример 10.
Вычислить площадь поверхности, полученной
вращением одной арки циклоиды
вокруг оси Ох.
Решение. По формуле (3.17) имеем
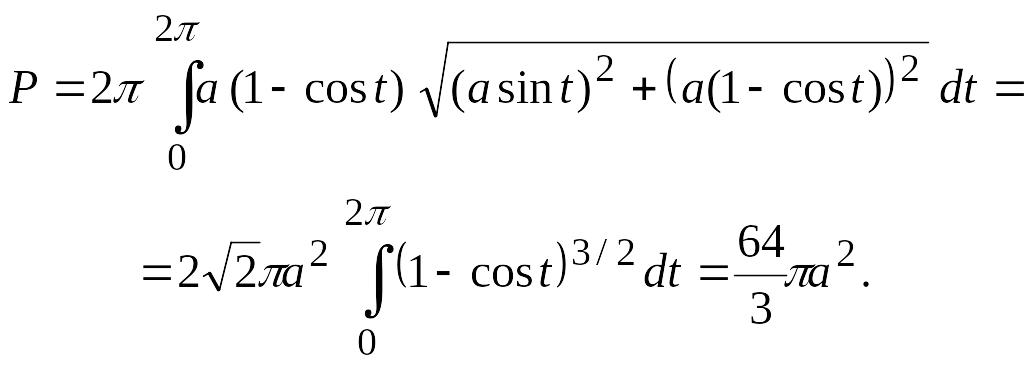
6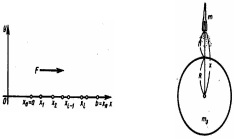
.
Работа переменной силы. Из
рассмотренных выше задач, связанных с
геометрическим приложением определенного
интеграла, следует, что для их решения
применяется один и тот же вычислительный
метод: приближенное значение искомой
величины представляется в виде
интегральной суммы, а затем предельным
переходом получается точное значение
в виде интеграла. С помощью этого же
метода решается целый ряд других задач
механики, физики и техники. В качестве
примера вычислим работу переменной
силы.
Рис. 17 Рис. 18
Пусть материальная точка перемещается под действием силы F, направленной вдоль оси Ох и имеющей переменную величину, зависящую от х. Требуется определить работу A, совершаемую силой F по перемещению материальной точки вдоль оси Ох из точки в точку ( ). Функция предполагается непрерывной на отрезке (рис. 17).
Разобьем произвольно
отрезок
на n
частей точками
Выберем на каждом частичном отрезке
точку
.
Сила, действующая на материальную точку
на отрезке
,
изменяется от точки к точке. Но если
длина отрезка мала, то значение силы в
точках отрезка
мало отличается от ее значения в любой
точке
,
так как
непрерывна.
Поэтому работу
,
совершаемую силой F
на
можно считать приближенно равной работе,
совершаемой на том же отрезке постоянной
силой
,
т. е.
Проводя аналогичные рассуждения для каждого отрезка разбиения, получаем приближенное значение работы A силы F на всем отрезке:
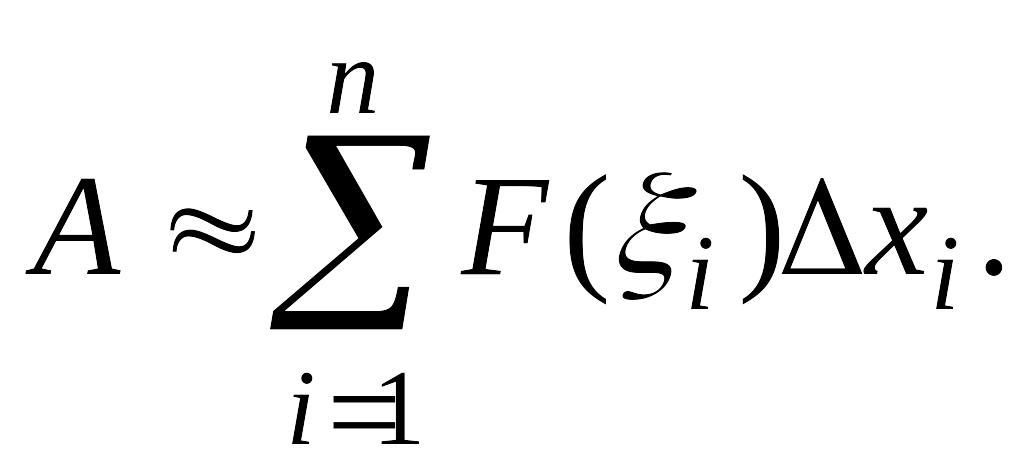
С другой стороны,
сумма в правой части равенства является
интегральной суммой для функции
.
Так как функция
непрерывна на
то предел этой суммы при
существует и равен определенному
интегралу от функции
по отрезку
Таким образом,
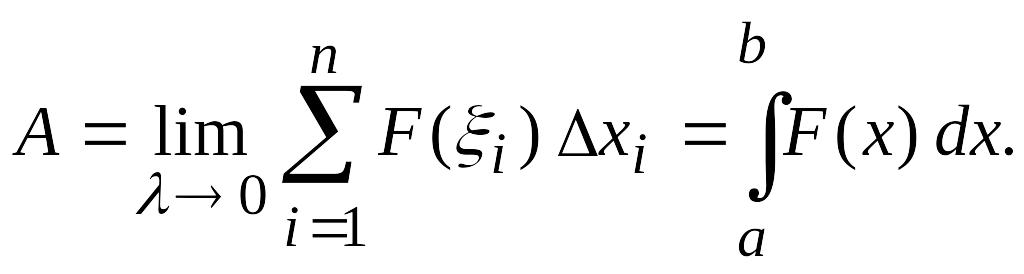(3.18)
Пример 11. Определить работу A, необходимую для запуска тела массой m с поверхности Земли вертикально вверх на высоту h (рис. 18).
Решение.
Обозначим через F
силу притяжения тела Землей. Пусть
-
масса Земли. Согласно закону Ньютона
где х
-
расстояние от тела до центра Земли.
Полагая
получаем
где R
– радиус Земли. При
сила
равна весу тела
,
т.е.
откуда
и
Таким образом, по формуле (3.18) получаем
