Интегрируемость непрерывных и некоторых разрывных функций Теорема 1. Если функция непрерывна на отрезке то она интегрируема на нем.
Как следует из теоремы, условие непрерывности функции является достаточным условием интегрируемости функции. Но это не означает, что определенный интеграл существует только для непрерывных функций. Класс интегрируемых функций шире. Так, например, существует определенный интеграл от функций, имеющих конечное число точек разрыва.
Теорема 2. Если функция ограничена на отрезке и непрерывна на нем всюду, кроме конечного числа точек, то она интегрируема на этом отрезке.
С л е д с т в и е. Кусочно-непрерывная на отрезке функция интегрируема на этом отрезке.
3.3. Основные свойства определенного интеграла
Интеграл
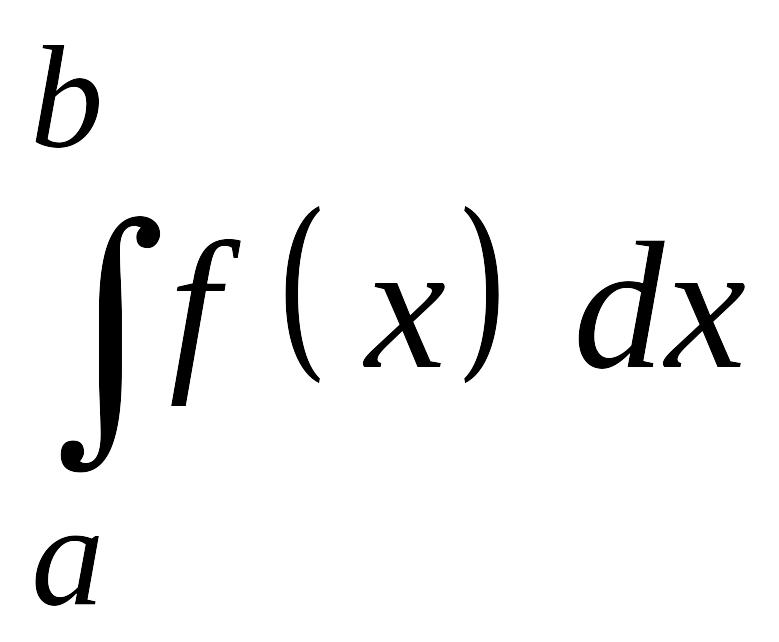был
введен для случая
.
Обобщим понятие определенного интеграла
на случай, когда пределы интегрирования
совпадают или нижний предел больше
верхнего. По
определению полагаем
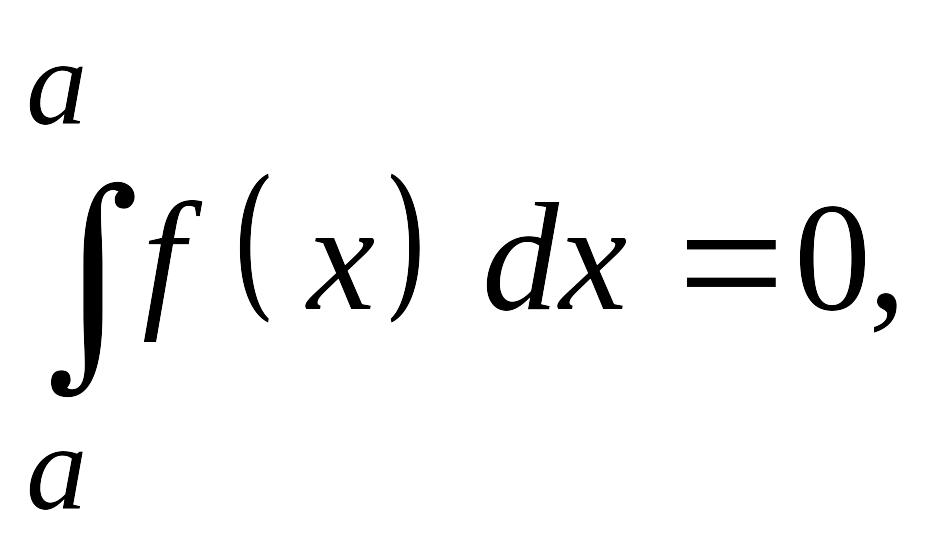(3.3)
рассматривая эту формулу как естественное распространение понятия определенного интеграла на отрезок нулевой длины.
Также по определению полагаем
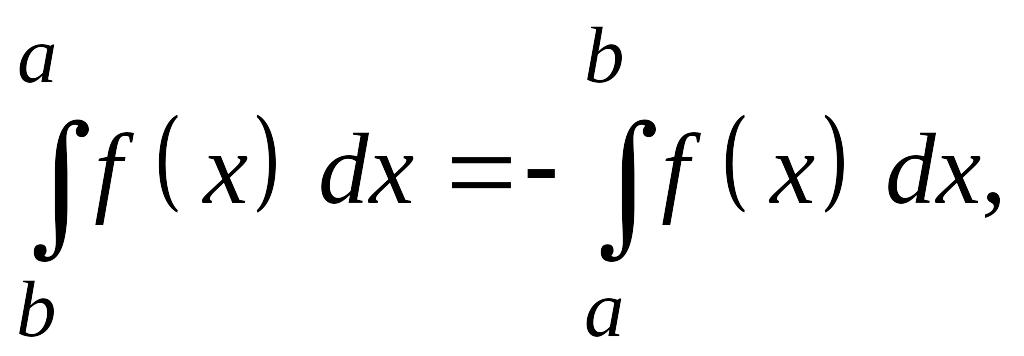(3.4)
рассматривая
формулу (3.4)
как естественное распространение
понятия определенного интеграла на
случай,
когда отрезок
при
пробегается в направлении от
к a. В этом
случае точки разбиения
отрезка
занумерованы в порядке следования от
b
к а и
в интегральной сумме все разности
имеют отрицательный знак.
Каковы бы ни
были числа a,
b,
c,
имеет место равенство
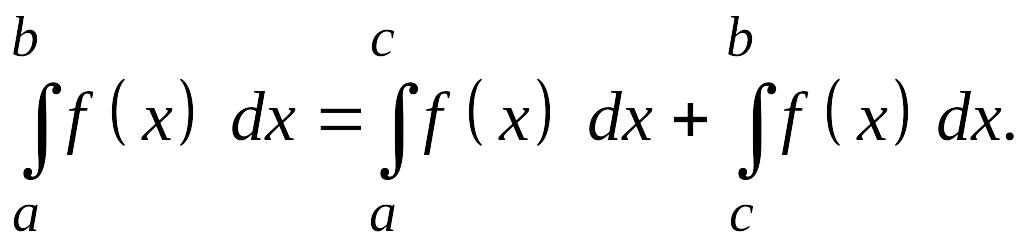
Постоянный
множитель можно выносить за знак
определенного интеграла,
т. е.
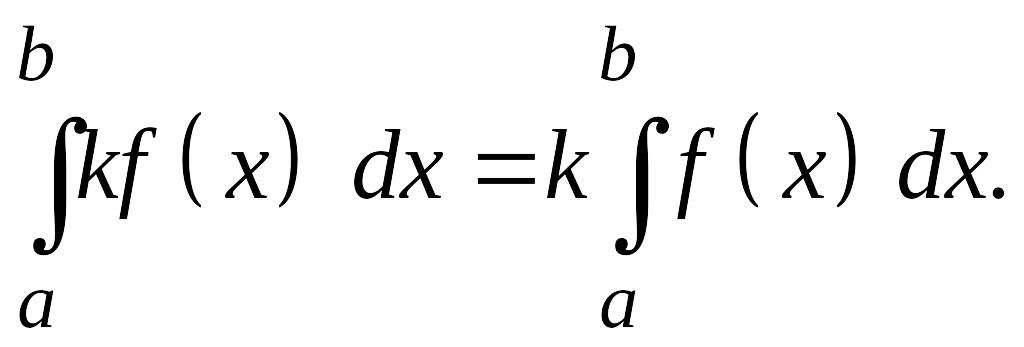
Определенный
интеграл от алгебраической суммы функций
равен алгебраической сумме их интегралов,
т.е.
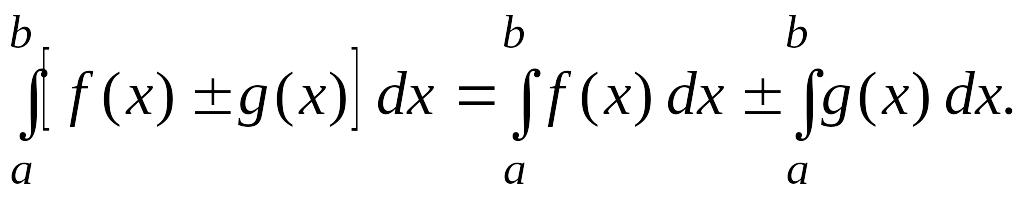
Оценки интегралов. Формула среднего значения
1. Оценки интегралов. Всюду в этом параграфе считаем, что .
Если всюду
на отрезке
функция
то
Если всюду на отрезке
то
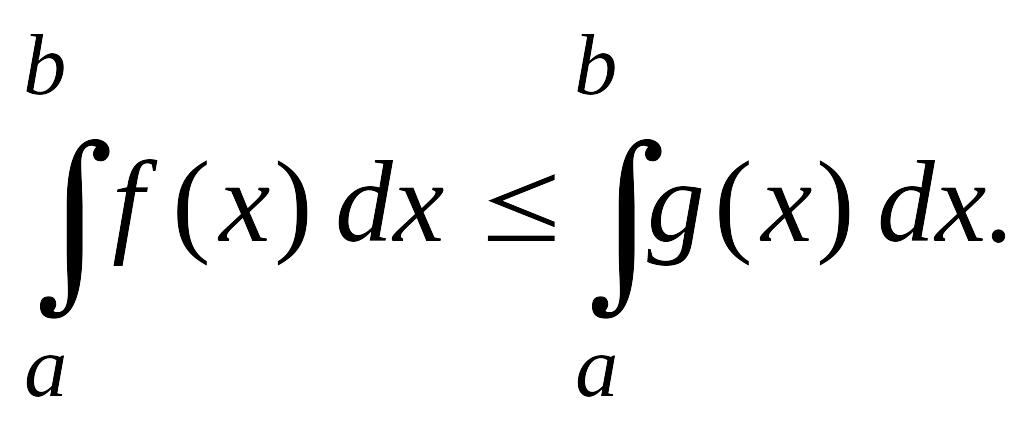
Для функции
,
определенной на отрезке
,
имеет место неравенство
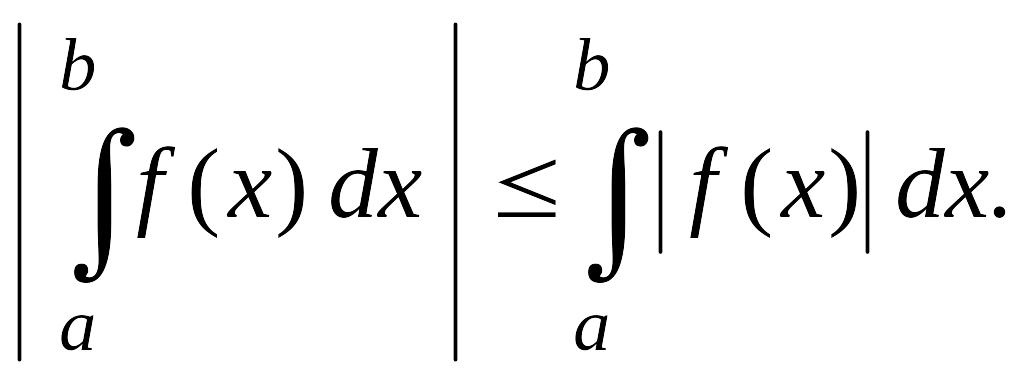
С л е д с т в и е.
Если всюду
на отрезке
то
Если m и М –
соответственно наименьшее и наибольшее
значения функции
на отрезке
,
то
2. Формула среднего значения.
Теорема (теорема о среднем). Если функция непрерывна на отрезке , то на этом отрезке существует такая точка с, что
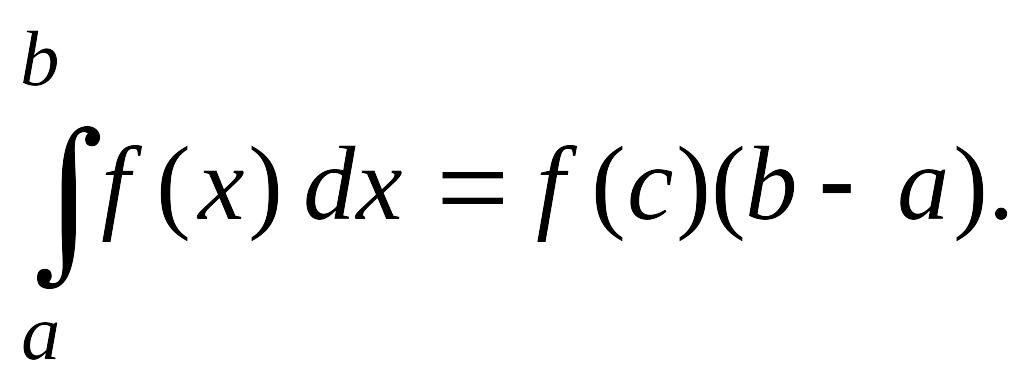
Последнее равенство
называется формулой
среднего значения,
а величина
– средним значением функции
на отрезке
З а м е ч а н и е.
Теорема о среднем имеет геометрический
смысл: величина определенного интеграла
при
равна площади прямоугольника, имеющего
высоту
и основание
.
Интеграл с переменным верхним пределом
До сих пор мы рассматривали определенный интеграл с постоянными пределами интегрирования a и b. Если изменять, например, верхний предел так, чтобы не выйти за пределы отрезка , то величина интеграла будет изменяться. Другими словами, интеграл с переменным верхним пределом представляет собой функцию своего верхнего предела.
Рассмотрим интеграл
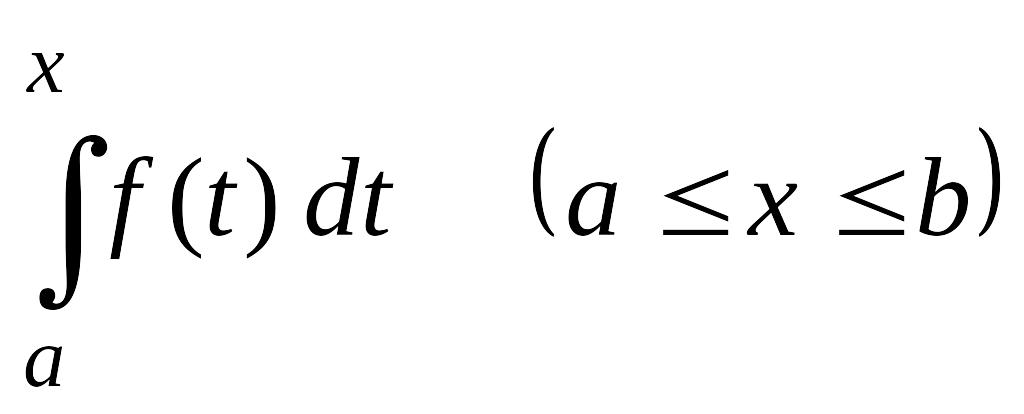
с постоянным нижним пределом а и переменным верхним пределом х. Величина этого интеграла является функцией
верхнего предела
х.
Обозначим эту функцию через
,
т.е. положим
(3.5)
и назовем ее
интегралом
с переменным верхним пределом.
Геометрически функция
представляет
собой площадь заштрихованной на рис. 5
криволинейной трапеции, если
.
Значение интеграла
с переменным верхним пределом раскрывает
следующая теорема.
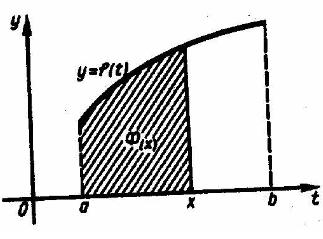
Рис. 5
Теорема.
Производная
интеграла от непрерывной функции по
переменному верхнему пределу существует
и равна значению подынтегральной
функции в точке, равной верхнему пределу,
т.е.
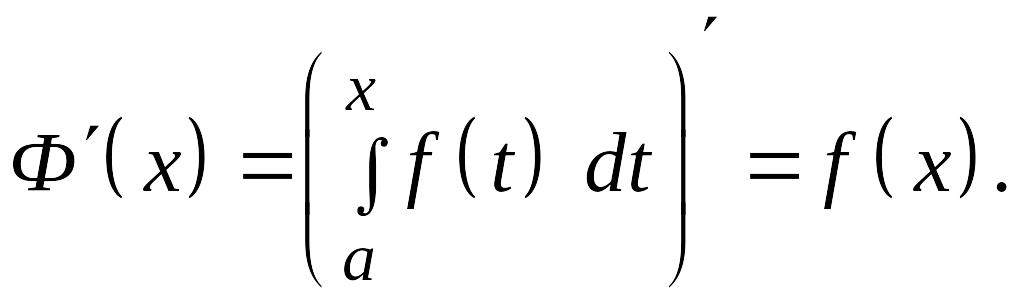
Таким образом,
установлено, что любая непрерывная на
отрезке
функция
имеет на этом отрезке первообразную,
причем функция
– интеграл с переменным верхним пределом
– является первообразной для
.
А так как всякая другая первообразная
для функции
может
отличаться от
только на постоянную, то установлена
связь между неопределенным и определенным
интегралами в виде
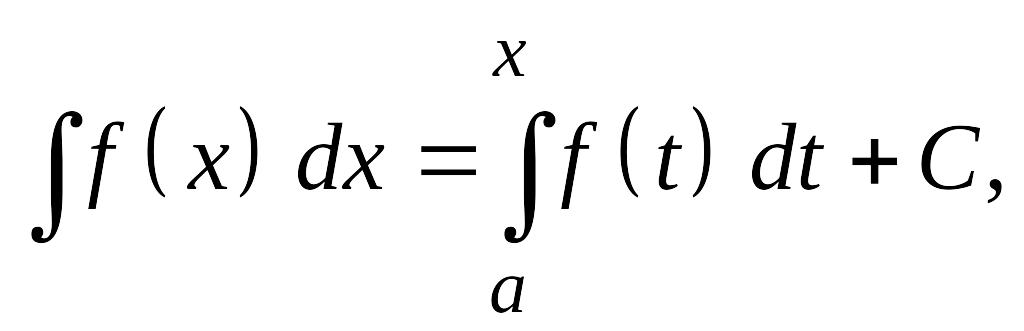где С
– произвольная постоянная.