1.6. Зависимость между a(ω), b(ω), f(ω)

Сравнив (11) и (13), получаем:

. (14)

Если учесть, что , , то легко можно получить

, (15)

Пример 4. Определить и построить спектральную плотность амплитуд прямоугольного импульса

Решение. Найдем спектральную плотность

Спектр , .

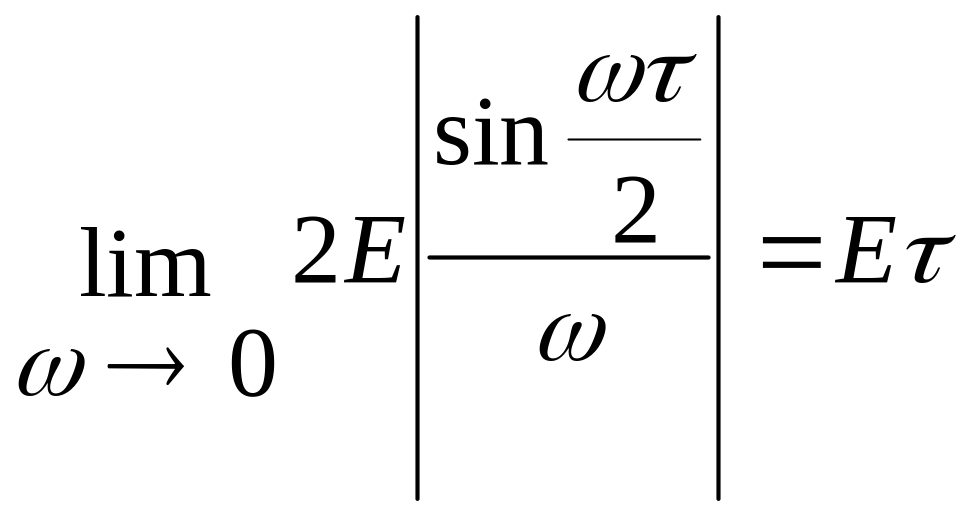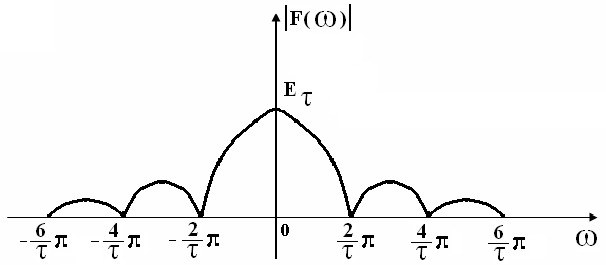
Для более точного построения графика найдем нули :

.

0

Рис. 8

2. Степенные ряды

2.1. Область сходимости степенного ряда

Функциональный ряд вида

, (16)

где, а- действительные числа называется степенным рядом, а числа - коэффициентами этого ряда.

Ряд(16) абсолютно сходится на интервале радиуса R с центром в точке x=a, т.е. при всех x удовлетворяющих неравенству │х-а│<R. Если R=0, то ряд сходится в одной точке x=a, если R= ∞ - на всей числовой оси. Для отыскания интервала сходимости следует составить ряд из абсолютных величин членов ряда (16) и исследовать его сходимость с помощью признаков Даламбера или Коши.

На концах интервала сходимости при x=a R ряд может как сходиться, так и расходиться, поэтому эти значения x следует подставить в ряд (16) и исследовать сходимость полученных числовых рядов. Таким образом, область сходимости степенного ряда состоит из его интервала сходимости и, возможно, граничных точек этого интервала.

Пример 5. Найти область сходимости ряда

Решение. Составим ряд из абсолютных величин и применим признак Даламбера:

Следовательно, ряд абсолютно сходится на интервале (-1; 3), а радиус сходимости R=2.

Подставив x=3 в заданный ряд, получим числовой ряд , который согласно интегральному признаку сходимости расходится.

При x=-1 получаем знакопеременный ряд , который по признаку Лейбница сходится условно. Следовательно, область сходимости заданного ряда – полуинтервал [-1; 3).

Пример 6. Найти область сходимости степенного ряда .

Решение. Применяя радикальный признак Коши к ряду, составленному из абсолютных величин, получим:

.

При получаем ряды, для которых не выполняется необходимый признак сходимости. Следовательно, область сходимости ряда – интервал .

Пример 7. Найти область сходимости ряда .

Решение. Применим признак Даламбера:

, следовательно, ряд сходится на всей числовой оси.

2.2. Ряд Тейлора

Рядом Тейлора для функции f(x) в окрестности точки x=a называется степенной ряд вида:

. (17)

В случае, когда a=0 ряд (17) называют рядом Маклорена. Из (17) очевидно, что необходимым условием разложения функции в ряд Тейлора является ее бесконечная дифференцируемость в точке x=a и ее окрестности.

Для разложения функции в ряд Тейлора можно использовать (17) или применять известные разложения, например:

,

, (18)

,

, . (19) (19)

При этом нередко приходится выполнять некоторые преобразования: представлять заданную функцию в виде суммы или разности более простых функций, вводить новые переменные, интегрировать и дифференцировать ряды. Однако следует помнить, что ряды (18) сходятся на всей числовой оси, а (19) только на интервале (-1; 1) и могут использоваться только при .

Пример 8. Разложить в ряд Маклорена функцию

.

Решение. Представим функцию в виде суммы двух простейших дробей:

.

Применяя к каждой дроби разложение (19), получим

, ,

, .

Следовательно

= + .

Радиус сходимости этого ряда .

Ряды Тейлора находят широкое применение в приближенных вычислениях. Например, при вычислении определенного интеграла разлагают в ряд Тейлора подынтегральную функцию, затем интегрируют полученные степенные функции и суммируют несколько первых слагаемых, обеспечивая заданную точность вычисления.

Пример 9. Вычислить с точностью до 0,001 интеграл .

Решение. Применяя первую из формул (18), получим

Тогда

Сумма знакочередующегося ряда не превышает первого члена ряда, поэтому все члены ряда, начиная с меньшего 0,001, отбрасываем:

.