ФГБОУ ВПО "Воронежский государственный

технический университет"

Кафедра высшей математики и

физико-математического моделирования

Функциональные ряды методические указания

к практическим и индивидуальным занятиям по разделам

«Степенные ряды» и «Ряды Фурье» курса «Математика» по направлению 211000.62 «Конструирование и технология электронных средств», профилю «Проектирование и технология радиоэлектронных средств» и направлению 200100.62 «Приборостроение», профилю «Приборостроение»

очной формы обучения

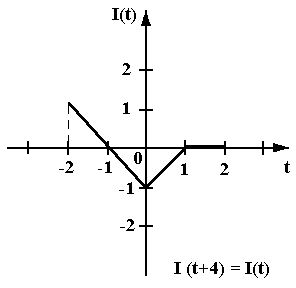
Воронеж 2013

Составители: канд. физ.-мат. наук Л.Д. Кретова, канд. физ.-мат. наук Н.Б. Ускова, канд. физ.-мат. наук A. В. Бондарев

УДК 517.9

Функциональные ряды: методические указания к практическим и индивидуальным занятиям по разделам «Степенные ряды» и «Ряды Фурье» курсов «Математика» » по направлению 211000.62 «Конструирование и технология электронных средств», профилю «Проектирование и технология радиоэлектронных средств» и направлению 200100.62 «Приборостроение», профилю «Приборостроение» очной формы обучения / ФГБОУ ВПО "Воронежский государственный технический университет"; сост. Л.Д. Кретова, Н.Б. Ускова, А. В. Бондарев. Воронеж, 2013. 36 с.

Данные методические указания предназначены для проведения практических и индивидуальных занятий для бакалавров направлений 211000.62 «Конструирование и технология электронных средств», профиля «Проектирование и технология радиоэлектронных средств» и 200100.62 «Приборостроение», профиля «Приборостроение» очной формы обучения факультета радиотехники и электроники во втором семестре на первом курсе. Разработка содержит необходимые краткие теоретические сведения, разобранные примеры, а также задачи для самостоятельного решения.

Предназначены для студентов первого курса.

Методические указания прдготовлены в электронном виде в текстовом редакторе Word и содержатся в файле Ряды1.doc

Ил. 8. Библиогр.: 5 назв.

Рецензент канд. физ.-мат. Наук, доц. Е.Г.Глушко

Ответственный за выпуск зав. кафедрой д-р физ.-мат. наук, проф. И.Л. Батаронов

Издается по решению редакционно-издательского совета Воронежского государственного технического университета

Ó ФГБОУ ВПО "Воронежский государствен-

ный технический университет", 2013

Справочный материал

1. Ряд и интеграл фурье

1.1. Ряд Фурье в действительной форме

Функциональный ряд вида

, (1)

где

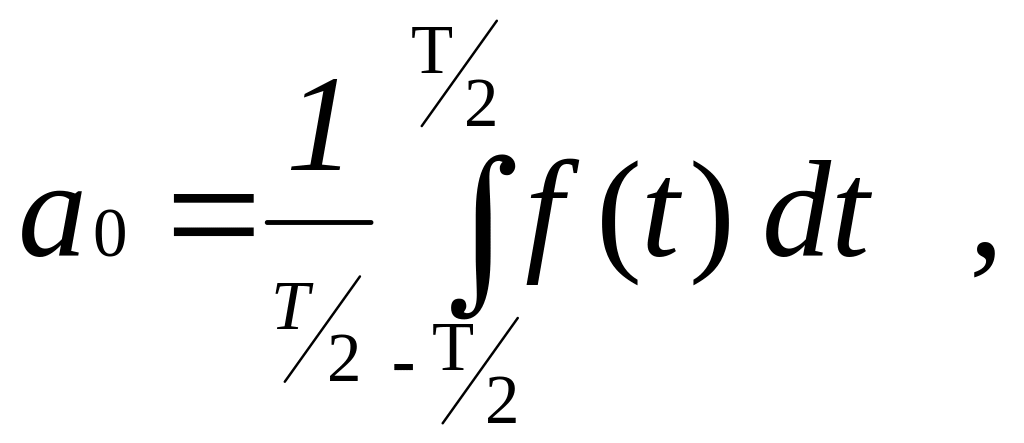
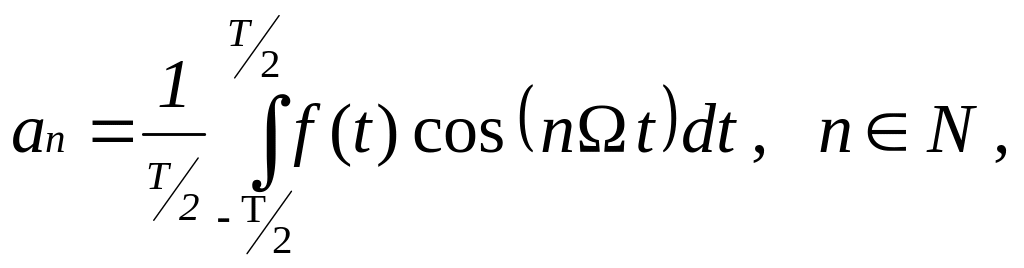(2) (2)

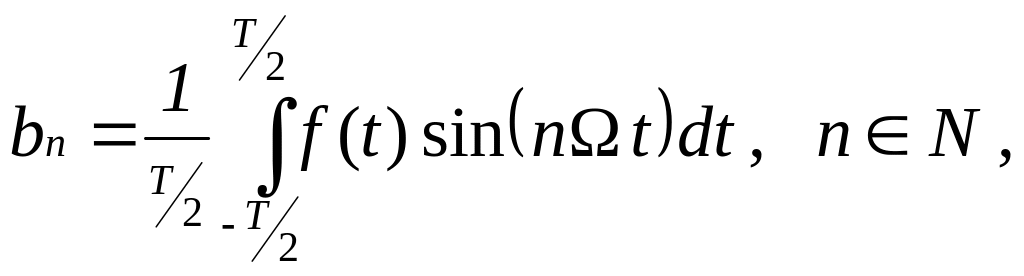
называется тригонометрическим рядом Фурье для функции f(t). Этот ряд сходится на всей числовой оси, если f(t) кусочно-монотонна и ограничена на отрезке и имеет период T. При этом в точках непрерывности функции сумма ряда S(t)=f(t), а в точках разрыва t=c: .

Если f(t) чётная функция, то

b_n=0,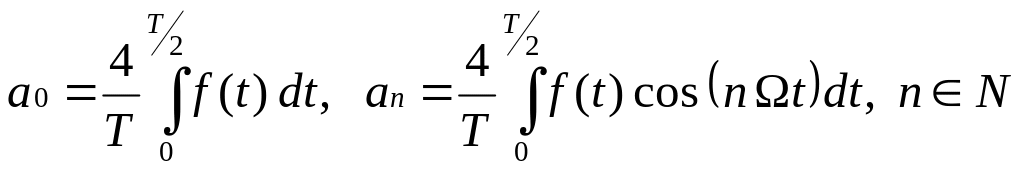 . (3)

Если f(t) – нечётная, то

a₀=0,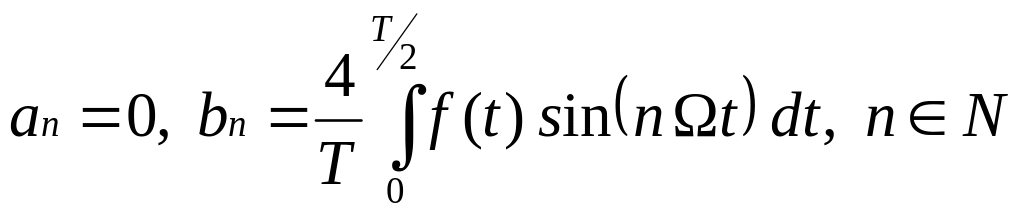 . (4)

Заметим, что для периодической функции 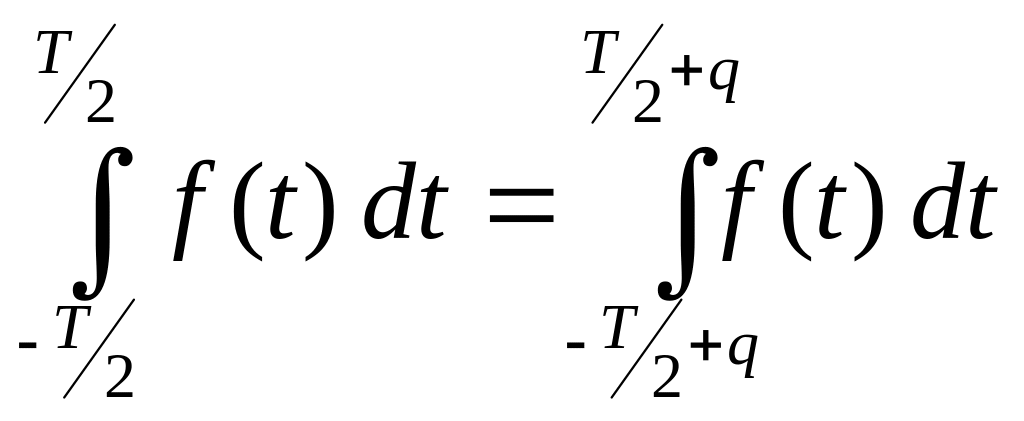, поэтому интегралы в формулах (2) – (4) можно вычислять по любому интервалу длиной Т.

Если воспользоваться соотношениями

, (5) (5)

то ряд (1) примет вид

, (6)

который обычно используется в различных прикладных задачах, так как имеет наглядный физический смысл. Каждое слагаемое под знаком суммы (6) описывает гармоническое колебание с амплитудой , частотой и начальной фазой . Эти параметры определяются однозначно из соотношений

(7)

Совокупность значений { } называют спектром амплитуд, а { } – спектром фаз.

Пример 1. Сигнал f(t) представляет собой периодическую последовательность прямоугольных импульсов напряжения:

.

Требуется представить f(t) рядом Фурье в действительной форме и построить графики f(t) и частичных сумм ряда S₁(t), S₂(t), S₃(t) на отрезке .

Решение. Вычислим коэффициенты ряда Фурье, используя нечётность функции f(t) (4):

.

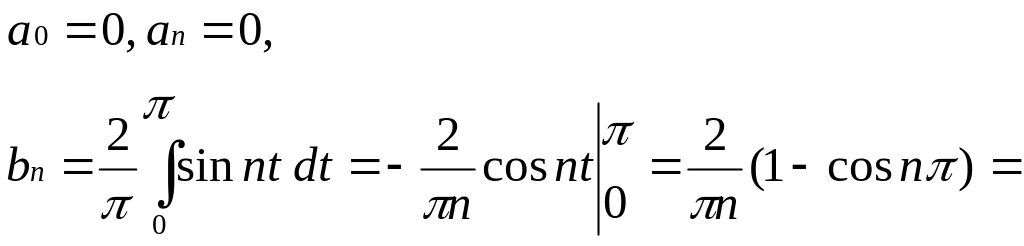
Следовательно, ряд Фурье имеет вид:

Это равенство справедливо при всех . При сумма ряда равна нулю.

На рис. 1 представлены графики функции f(t) и частичной суммы ряда На рис. 2 штрихами изображены графики S₁(t) и , а сплошной линией – график На рис. 3 штрихами изображены графики S₂(t) и , а сплошной линией –

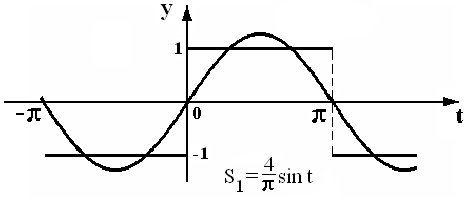
Рис.1

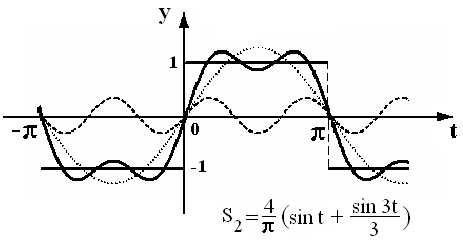
Рис. 2

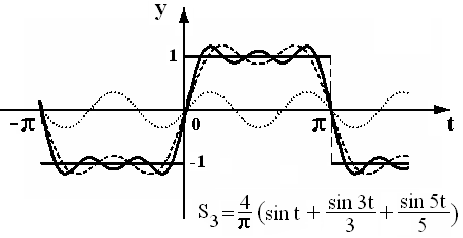
Рис. 3