4.2.1.2. Приложение расклинивающей силы к кривошипу

В данном случае задача определения величины расклинивающей силы при α=0 аналогична предыдущей (схема сил и моментов показана на рис. 4.10).

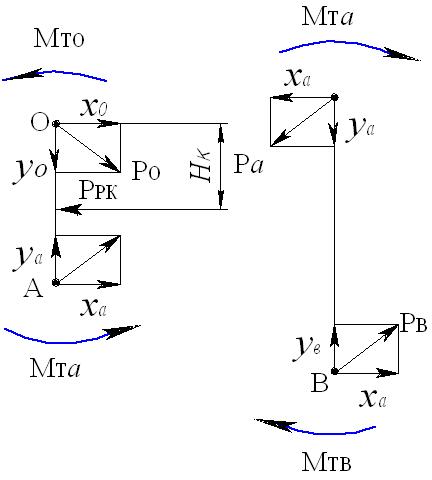
Рис. 4.10. Схема сил и моментов, действующих на элементы

кривошипно-шатунного механизма, при приложении

расклинивающей силы к кривошипу

Условия равновесия элементов расчлененного кривошипно-шатунного механизма (рис. 4.10. а и 4.10.б) следующие:

для кривошипа

; (4.29)

; (4.30)

; (4.31)

для шатуна

; (4.32)

; (4.33)

. (4.34)

На рис. 4.10, кроме принятых ранее обозначений, Н_к – плечо силы Р_рк на кривошипе, равное наименьшему расстоянию от её линии действия до оси кривошипа (точка О). При этом Н_к может быть как больше, так и меньше R.

В результате рассмотрения формул (4.32 – 4.34) определяем, что

, (4.35)

где:

. (4.36)

Учитывая значение х_а, выраженное формулой (4.35), при решении уравнений (4.29 – 4.31), находим

, (4.37)

где

; (4.38)

. (4.39)

Как и в предыдущем случае, полученные формулы могут быть значительно упрощены. Учитывая, что и , для , получим

. (4.40)

Как показывают расчеты, для случаев погрешность вычисления по формуле (4.40) не более 5%.

Формулы для вычисления расклинивающей силы Р_рк, прикладываемой к кривошипу с одновременным включением муфты при разогнанном приводе, могут быть получены следующим образом.

Условие равновесия кривошипа (4.31) для данного случая запишется

. (4.41)

Решая это уравнение с учетом формул (4.29) и (4.35) относительно , получим

, (4.42)

где

; (4.43)

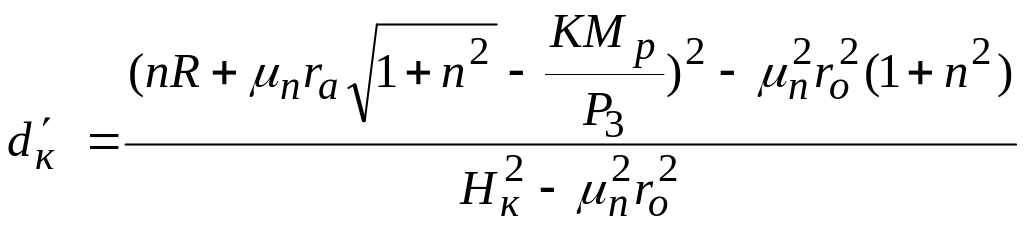. (4.44)

Упрощенная формула для определения , получаемая при допущениях, принятых при выводе формулы (4.40), имеет вид

. (4.45)

4.2.1.3. Приложение расклинивающей силы к рычагу

Асимметричное приложение Р_рр по отношению к опорам кривошипного вала несколько усложняет задачу по сравнению с предыдущими.

Для решения её также расчленим кривошипно-шатунный механизм на части (рис.4.11) и составим условие равенства действующих на кривошипном валу моментов относительно его оси (4.11.а) при α=0.

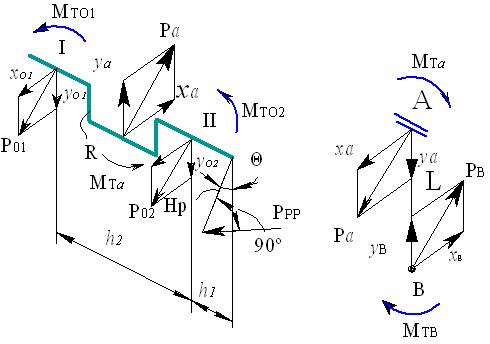
Рис. 4.11. Схема сил и моментов, действующих на элементы

кривошипно-шатунного механизма, при приложении

расклинивающей силы к рычагу на кривошипном валу

Это условие может быть представлено в следующем виде

, (4.46)

где, кроме принятых ранее обозначений:

Н_р – длина рычага;

М_ТО , М_ТО – моменты трения в опорах I и II кривошипного вала.

Уравнение (4.46) является основным для определения величины Р_рр.

Величины х_а и М_Та, входящие в уравнение (4.46), могут быть определены, исходя из условий равновесия шатуна для данного случая (рис. 4.11.б).

Эти условия аналогичны условиям равновесия шатуна при приложении расклинивающей силы к кривошипу – формулы (4.32 – 4.34). Поэтому, как и в предыдущем случае, величина х_а может быть найдена по формуле (4.35).

Следовательно

. (4.47)

Для определения М_ТО и М_ТО найдем вертикальные и горизонтальные составляющие реакции опор и от действия сил Р₃, х_а и Р_рр.

На рис. 4.11 видно, что при = 0

; (4.48)

; (4.49)

, (4.50)

где:

h₁ – наименьшее расстояние от оси рычага до линии действия равно-действующей реакции в ближайшем коренном подшипнике эксцентрикового вала;

h₂ – то же, между линиями действия равнодействующих реакций в коренных подшипниках эксцентрикового вала.

В этом случае

; (4.51)

. (4.52)

Тогда

; (4.53)

. (4.54)

С учетом формул (4.35), (4.47), (4.53) и (4.54) при уравнение (4.46) приобретает вид

. (4.55)

Решение этого уравнения относительно Р_рр при известном Н_р позволяет определить необходимую величину расклинивающей силы.

Следует отметить, что решение уравнения (4.55) относительно Р_рр вызывает трудности, поэтому целесообразно решить обратную задачу, а именно: – задаваясь приемлемыми значениями силы расклинивания Р_рр определить соответствующие длины рычага Н_р.

Полученные решения позволяют определить зависимость

. (4.56)

Построив график зависимости , находим по нему величину Р_рр, соответствующую заданному значению Н_р.

При и (что справедливо при ) выражение (4.55) примет вид

, (4.57)

и, учитывая, что и , получим

. (4.58)

Расчеты показывают, что погрешность вычислений по приближенной формуле (4.58) при не более 5%. Поэтому данная формула может быть рекомендована в качестве основной (обратим внимание: формула (4.58) подобна формуле (4.40), что свидетельствует и о физической аналогии этих разновидностей способа).

В приведенном нами случае величина необходимой расклинивающей силы также может быть уменьшена с помощью привода.

Основные расчетные формулы для определения её величины в данном случае легко получаются из условия равенства моментов на кривошипном валу

(4.59)

и имеют вид

(4.60)

и

. (4.61)