
- •Введение
- •1. Лекции
- •1.1. Проблемная лекция
- •1. Тема «Кривые второго порядка»
- •2. Тема «Свойства функций, непрерывных на отрезке»
- •3. Тема «Обыкновенные дифференциальные уравнения»
- •1.2 Лекция-визуализация
- •1.3. Лекция-конференция
- •1.4. Лекция-беседа
- •2. Практические занятия
- •2.1. Лабораторные работы
- •2.2. Элементы компьютерных симуляций
- •2.3. Дидактические игры
- •2.4. Решение сюжетных и профессионально-ориентированных задач
- •2.5. Составление опорных конспектов
- •Основные виды обыкновенных дифференциальных уравнений первого порядка
- •Обыкновенные дифференциальные уравнения второго порядка, допускающие понижение порядка
- •Исследование знакопеременного ряда на сходимость
- •3. Самостоятельная работа студентов
- •На сайте http://www.Mathtest.Ru (тесты по математике online) можно за 15 минут или быстрее проверить свой уровень знаний по математике за любой раздел первого курса.
- •3.1. Использование рабочих тетрадей
- •Фрагмент рабочей тетради по теме «Кратные интегралы»
- •Задачи для самостоятельного решения:
- •Фрагменты рабочей тетради по теме «Степенные ряды»
- •3.2. Работа над учебными проектами
- •4) Проект «Сборник профессиональных задач»
- •5) Проекты, связанные с опредмечиванием математических объектов
- •6) Игровые проекты
- •3.3. Обучающее тестирование
- •Литература
- •Оглавление
- •4) Проект «Сборник профессиональных задач» 134
- •5) Проекты, связанные с опредмечиванием математических объектов 137
- •6) Игровые проекты 138
- •394006 Воронеж, ул. 20-летия Октября, 84
3. Тема «Обыкновенные дифференциальные уравнения»
Обычно изложению темы «Обыкновенные дифференциальные уравнения» предшествует рассмотрение практической задачи из какой-либо предметной области, приводящей к дифференциальному уравнению.
Однако общая постановка задач, приведших к появлению дифференциальных уравнений, возникла не из запросов практики, а в недрах самой математики. Как только задачи на проведение касательных к кривым свелись к вычислению производных, они потеряли свою привлекательность для ученых. Их решение теперь состояло в применении известных правил и не требовало творчества. Внимание математиков переключается на более сложные обратные задачи на касательные. Так назывались задачи, в которых требуется найти кривые по заданным свойствам касательных к ним.
Первые обратные задачи на касательные сформулировал в 1638 г. французский математик Флоримон де Бон.
В этой связи студентам можно сначала предложить, например, такую задачу: Найти все кривые, обладающие следующим свойством: если в любой точке кривой провести касательную, то отрезок касательной, заключенный между осями координат, будет делиться в точке касания пополам (рис. 1.4).
Р ешение.
Пусть
ешение.
Пусть
 – искомая кривая. Обозначим через X
и Y
координаты точек касательной к этой
кривой и запишем уравнение этой
касательной в точке
– искомая кривая. Обозначим через X
и Y
координаты точек касательной к этой
кривой и запишем уравнение этой
касательной в точке
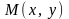 :
:
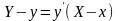 .
.
Найдем точки пересечения касательной с осями координат:
A:
X = 0  ;
B:
Y = 0
;
B:
Y = 0 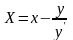 .
.
Так как точка касания M – середина отрезка AB, то
 и
и
 ,
,
откуда следует, что искомая кривая должна удовлетворять соотношению
 .
.
Для решения задачи по ее условию составлено уравнение, выражающее зависимость между искомой функцией, ее аргументом и производной; оно называется дифференциальным.
Легко
убедиться, что функции вида
 ,
где C
– произвольная постоянная, дают все
решения полученного уравнения:
,
где C
– произвольная постоянная, дают все
решения полученного уравнения:
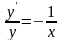 ,
,
 ,
,
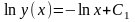
(две первообразные одной функции отличаются на постоянную),
 (
(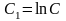 ),
.
),
.
Далее, поскольку к дифференциальным уравнениям приводит множество практических задач, полезно рассмотреть также другие, сначала достаточно простые, затем – более содержательные, задачи из физики, техники, экономики или других областей, приводящие к дифференциальным уравнениям: о радиоактивном распаде, об охлаждении тела, о движении моторной лодки, о потере заряда проводником, о концентрации раствора, об износе оборудования, о зависимости давления воздуха от высоты над уровнем моря и т. п. Сюжет задачи определяется направлением подготовки студентов [1], [3], [11], [16].
Например, студентам технических направлений можно предложить установить зависимость между переменной массой и скоростью летящей ракеты [47].
Рассмотрим
движение ракеты в космосе. Для простоты
пренебрежем всеми внешними силами,
действующими на ракету. Основными
параметрами, характеризующими ракету
и ее двигатель, являются:
 – скорость
истечения газов из сопла ракеты
относительно корпуса ракеты, для простоты
считаем ее постоянной, она зависит
от вида применяемого топлива;
– скорость
истечения газов из сопла ракеты
относительно корпуса ракеты, для простоты
считаем ее постоянной, она зависит
от вида применяемого топлива;
 –
исходная масса ракеты с горючим;
–
исходная масса ракеты с горючим;
 –
конечная масса ракеты после выгорания
всего горючего.
–
конечная масса ракеты после выгорания
всего горючего.
Напишем
уравнение движения ракеты, считая, что
она движется по прямой линии. Пусть
 – координата ракеты (вдоль этой прямой)
в момент времени
t;
– координата ракеты (вдоль этой прямой)
в момент времени
t;
 –
скорость ракеты в момент времени
t;
–
скорость ракеты в момент времени
t;
 –
масса ракеты в момент времени
t
(эта
масса уменьшается по мере сгорания
горючего).
–
масса ракеты в момент времени
t
(эта
масса уменьшается по мере сгорания
горючего).
Воспользуемся
законом сохранения импульса (количества
движения). При этом удобно ввести
мгновенную систему координат, связанную
с летящей ракетой (точнее, равномерно
движущуюся той скоростью, с которой
ракета движется в момент времени
t).
В
этой системе координат скорость ракеты
(и имеющегося в ней топлива) в момент
времени
t
равна
нулю. Рассмотрим момент времени
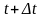 в
этой же системе координат. Предположим,
что за это время в ракете сгорело и
вылетело из нее топливо массой
в
этой же системе координат. Предположим,
что за это время в ракете сгорело и
вылетело из нее топливо массой
 .
Скорость самой ракеты (с остатками
топлива увеличилась на
.
Скорость самой ракеты (с остатками
топлива увеличилась на
 и
в рассматриваемой системе координат
стала равной
и
в рассматриваемой системе координат
стала равной
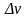 ,
в то время как скорость вылетевшего
топлива равна
,
в то время как скорость вылетевшего
топлива равна
 (с
учетом направления).
(с
учетом направления).
Суммарный
импульс в момент
примерно
равен
 с точностью, растущей с уменьшением
с точностью, растущей с уменьшением
 (здесь
неточность связана с тем, что со временем
меняется масса
(здесь
неточность связана с тем, что со временем
меняется масса
 и, кроме того, скорость вылета горючего
в рассматриваемой системе координат
будет равна
лишь
в момент времени t,
так как дальше сама ракета начнет
двигаться). Приравнивая суммарный
импульс к нулю, получим
и, кроме того, скорость вылета горючего
в рассматриваемой системе координат
будет равна
лишь
в момент времени t,
так как дальше сама ракета начнет
двигаться). Приравнивая суммарный
импульс к нулю, получим
 .
.
Деля
обе части на
и
переходя к пределу при
 ,
получим точное равенство (дифференциальное
уравнение)
,
получим точное равенство (дифференциальное
уравнение)
 .
.
Это уравнение легко решается и без знания специальных приемов:
 ,
или
,
или
 ,
откуда
,
откуда
 .
.
При 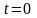
 ,
,
 и уравнение принимает вид
и уравнение принимает вид
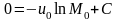 ,
т. е.
,
т. е.
 ,
поэтому
,
поэтому
 .
.
В момент,
когда все топливо израсходовано, получим
 ,
,
 .
.
Эта формула называется формулой Циолковского.
Ракета может достичь скорости, большей, чем скорость истечения газов из сопла, хотя для этого отношение массы ракеты с топливом к массе ракеты без топлива должно быть очень велико. Для увеличения отношения на разных этапах полета ракеты делают многоступенчатыми.
Можно отметить, что полученная формула годится лишь для движения в вакууме и при отсутствии силы тяжести. Учет сопротивления воздуха и земного тяготения намного усложняет дифференциальное уравнение.
Изложение
темы «Решение
линейных однородных дифференциальных
уравнений второго порядка с постоянными
коэффициентами»
в учебных пособиях начинается обычно
так: «Пусть дано однородное дифференциальное
уравнение второго порядка
 ,
где p
и q
– постоянные действительные числа.
Будем искать частные решения в виде:
,
где p
и q
– постоянные действительные числа.
Будем искать частные решения в виде:
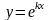 ,
где
,
где
 ;
тогда
;
тогда
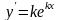 ,
,
 ,
...» и т. д.
,
...» и т. д.
Искусственность этого приема вызывает у студентов вопрос: «А каким образом можно все же догадаться искать решения данного уравнения именно в форме ?»
Более
правильным можно считать следующий
прием решения этого вопроса. Левая часть
этого уравнения представляет собой
сумму самой функции y
и ее производных
 ,
взятых с некоторыми постоянными
коэффициентами. Чтобы такая сумма
тождественно равнялась нулю, надо чтобы
,
взятых с некоторыми постоянными
коэффициентами. Чтобы такая сумма
тождественно равнялась нулю, надо чтобы
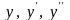 были похожи, отличались друг от друга
постоянными множителями. Поэтому,
например, ни одна из функций
были похожи, отличались друг от друга
постоянными множителями. Поэтому,
например, ни одна из функций
 ,
,
 ,
,
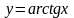 ,
,
 никак не может оказаться решением
данного уравнения.
никак не может оказаться решением
данного уравнения.
Аудитории
ставится вопрос: «Не помните ли такую
функцию, у которой производные похожи
на саму функцию?» Ответ: «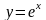 ,
,
,
, ,
...» –обычно поступает немедленно. Только
после этого можно заявить: «Итак, частные
решения будем искать в виде
».
,
...» –обычно поступает немедленно. Только
после этого можно заявить: «Итак, частные
решения будем искать в виде
».
