4) Проект «Сборник профессиональных задач»

Студенты изучают приложения математики в области их будущей профессиональной деятельности, например, в социально-экономической сфере.

Так, к необходимости использования второго замечательного предела приводит задача о непрерывном начислении процентов.

Рассмотрим пример Я. И. Перельмана, дающий интерпретацию числа e в задаче о сложных процентах. В сбербанках процентные деньги присоединяются к основному капиталу ежегодно. Если присоединение совершается чаще, то капитал растет быстрее, так как в образовании процентов участвует большая сумма. Возьмем чисто теоретический, весьма упрощенный пример. Пусть в банк положено 100 ден. ед. из расчета 100% годовых. Если процентные деньги будут присоединены к основному капиталу лишь по истечении года, то к этому сроку 100 ден. ед. превратятся в 200 ден. ед. Посмотрим теперь, во что превратятся 100 ден. ед., если процентные деньги присоединять к основному капиталу каждые полгода. По истечении полугодия мы получим 150 ден. ед., а еще через полгода – 150  1,5 = 225 (ден. ед.). Если присоединение де­лать каждые 1/3 года, то по истечении года мы получим 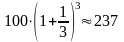 (ден. ед.). Будем учащать сроки присоеди­нения процентных денег до 0,1 года, до 0,01 года, до 0,001 года и т. д. Тогда из 100 ден. ед. спустя год получится: 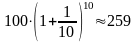 (ден. ед.).;

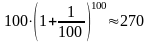 (ден. ед.); 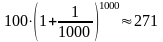 (ден. ед.).

При безграничном сокращении сроков присоединения процентов наращенный капитал не растет беспредельно, а приближается к некоторому числу, равному приблизительно 272. Более чем в 2,72 раз капитал, положенный под 100% годовых, увеличиться не может, даже если бы наросшие процен­ты присоединялись к капиталу ежесекундно, потому что число е = 2,71828… и .

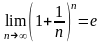В практических расчетах в основном применяют дискретные проценты, т.е. проценты, начисляемые за фиксированные одинаковые интервалы времени (год, полугодие, квартал, месяц и т. д.). Время – дискретная переменная. В некоторых случаях – в доказательствах и расчетах, связанных с непрерывными процессами, – возникает необходимость в применении непрерывных процентов. Рассмотрим формулу сложных процентов:

.

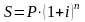Здесь P – первоначальная сумма; i – ставка процентов (в виде десятичной дроби); S – сумма, образовавшаяся к концу срока ссуды в конце n-го года.

Рост по сложным процентам представляет собой процесс, развивающийся по геометрической прогрессии. Присоединение начисленных процентов к сумме, которая служила базой для их определения, называют капитализацией процентов. В финансовой практике часто сталкиваются с задачей, обратной определению наращенной суммы: по заданной сумме S, которую следует уплатить через некоторое время n, необходимо определить сумму полученной ссуды P. В этом случае говорят, что сумма S дисконтируется, а проценты в виде разности S – P называют дисконтом. Величину P, найденную дисконтированием S, называют современной, или приведенной величиной S. Имеем:

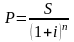, следовательно, .

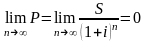Таким образом, при очень больших сроках платежа совре­менная величина последнего будет крайне незначительна.

В практических финансово-кредитных операциях непрерывные процессы наращения денежных сумм, т. е. наращения за бесконечно малые промежутки времени, применяются редко. Существенно большее значение непрерывное наращение имеет в количественном финансово-экономическом анализе сложных производственных и хозяйственных объектов и явлений, например, при выборе и обосновании инвестиционных решений. Необходимость в применении непрерывных наращений (или непрерывных процентов) определяется, прежде всего, тем, что многие экономические явления по своей природе непрерывны, поэтому аналитическое описание в виде непрерывных процентов более адекватно, чем на основе дискретных.

Обобщим формулу сложных процентов для случая, когда проценты начисляются m раз в году: .

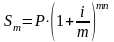Наращенная сумма при дискретных процессах находится по этой формуле, здесь m – число периодов начисления в году; i – годовая или номинальная ставка. Чем больше т, тем меньше промежутки времени между моментами начисления процентов. В пределе при 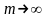 имеем:

.

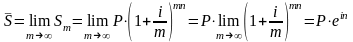При непрерывном наращении процентов применяют особый вид процентной ставки – силу роста, которая характеризует относительный прирост наращенной суммы в бесконечно малом промежутке времени. При непрерывной капитализации процентов наращенная сумма равна конечной величине, зависящей от первоначальной суммы, срока наращения и номи­нальной ставки процентов. Для того чтобы отличить ставку непрерывных процентов от ставки дискретных процентов, ее обозначают через . Тогда 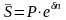. Сила роста  представляет собой номинальную ставку процентов при . Множитель наращения рассчитывается с помощью компьютера или по таблицам функции.

Затем они составляют и решают задачи по изученному материалу. Возможные варианты таких задач приводятся далее.

Пример 1. Начальная сумма вклада составляет 30000 руб., а ставка начисления за год 5%. Найти:

а) накопленную сумму и проценты за первые 3 года;

б) проценты за третий год;

в) накопленную сумму за 6 лет;

г) проценты за последние 3 года.

Решение

а) Накопленная сумма, согласно формуле сложных процентов , равна 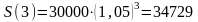 (руб.), а проценты за тот же период представляют разность 34729 – 30000 = 4729 (руб.).

б) Проценты за третий год определяем по формуле:

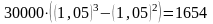 (руб.).

в) Накопленная сумма за 6 лет будет равна:

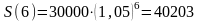 (руб.).

г) Наконец, найдем проценты за последние 3 года:

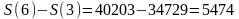 (руб.).

Пример 2. Первоначальный вклад, положенный в банк под 4% годовых, составил 70000 руб. Найти размер вклада через 4 года и 3 месяца при начислении процентов:

а) поквартальном; б) помесячном; в) непрерывном.

Решение.

а) Используем формулу для начисления процентов m раз в году:

.

В нашем случае P = 70000; i = 0,04; п = 4,25; т = 4. Имеем:

.

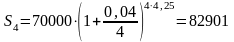б) Если проценты начисляются каждый месяц, то т = 12, и конечная сумма будет равна: .

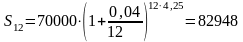в) Используем формулу для непрерывного начисления процентов: .

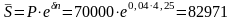Пример 3. Вклад был положен в банк на 3 года и в конце срока составлял 750 долларов. Каков был первоначальный капитал, если годовая процентная ставка составляла 5% и проценты начислялись непрерывно?

Решение. По формуле непрерывного начисления процен­тов имеем:

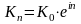, откуда .

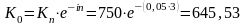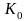Здесь через обозначена величина первоначального вклада, через 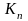– величина вклада через n лет.

Пример 4. Вклад пролежал в банке 3 года и 6 месяцев и в конце срока составил 10000 руб. Первоначальный вклад был равен 8765 руб. Каков был размер номинальной процентной годовой ставки, если проценты начислялись непрерывно?