
- •Часть 2
- •( Кафедра «высшей математики и физико-математического моделирования») методические указания
- •Часть 2
- •Введение
- •1. Неопределенный интеграл
- •2. Определенный интеграл и его приложения
- •3. Несобственные интегралы
- •2) Вычисление объёмов тел по известным поперечным сечениям
- •1. Функции нескольких переменных Основные теоретические сведения
- •6. Дифференцирование сложной функции
- •7. Производная по направлению. Градиент функции и его свойство
- •8. Производные и дифференциалы высших порядков
- •9. Дифференцирование неявных функций.
- •Касательная плоскость и нормаль к поверхности
- •8. Формула Тейлора для функции двух переменных
- •12. Экстремум функции нескольких независимых переменных
- •13. Условный экстремум. Наибольшее и наименьшее значения функции в замкнутой области
- •14. Дифференциальные уравнения
- •15. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •16. Система линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •Заключение
- •Библиографический список
- •Часть 2
- •Федотенко Галина Федоровна в авторской редакции
6. Дифференцирование сложной функции
Случай одной независимой переменной.
Если
есть дифференцируемая функция двух
аргументов x
и y
в некоторой области D
плоскости XOY,
которые в свою очередь являются
дифференцируемыми функциями независимой
переменной t,
то есть
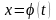 ,
,
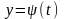
![]() ,
то сложная функция
,
то сложная функция
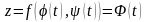 - есть функция одной переменной t
и имеет место равенство
- есть функция одной переменной t
и имеет место равенство
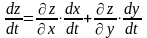
В
частности, если t
совпадает с одним из аргументов, например,
t=x,
то справедлива формула
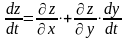 ,
и
,
и
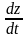
![]() называется полной производной функции
z
по x.
называется полной производной функции
z
по x.
Пример.
Найти
,
если
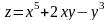 ,
где
,
где
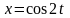 ,
,
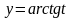 .
.
Решение.
Воспользуемся формулой (1). Предварительно
находим
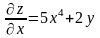 ,
,
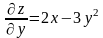 ,
,
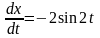 ,
,
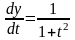 .
Тогда
.
Тогда
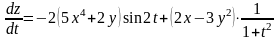
![]()
Пример.
Найти частную производную
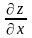
![]() и полную производную
и полную производную
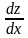 ,
если
,
если
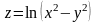 ,
где
,
где
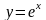 .
.
Решение.
Имеем
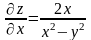 .
Находим
.
Находим
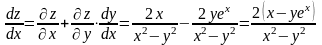
Случай нескольких независимых переменных.
Если
z
есть сложная функция нескольких
переменных, например
,
где аргументы x,
y,
так называемые промежуточные переменные,
являются функциями независимых переменных
u,
v:
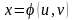 ,
,
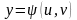 ,
то сложная функция
,
то сложная функция
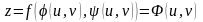 фактически является функцией двух
«конечных» переменных u,
v.
Если функции
фактически является функцией двух
«конечных» переменных u,
v.
Если функции
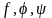 — дифференцируемые функции, то частные
производные по
— дифференцируемые функции, то частные
производные по
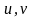 выражаются так:
выражаются так:
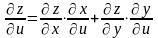 ,
или
,
или
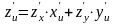
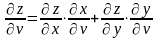 ,
или
,
или
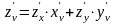
Структура этих формул сохраняется и при большем числе переменных.
Пример.
Найти
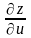 и
и
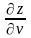 ,
если
,
если
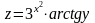 ,
,
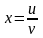 ,
,
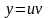
Решение:
Находим
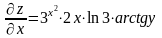 ;
;
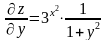 ;
;
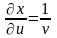 ;
;
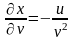 ;
;
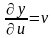 ;
;
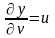 ;
;
Подставляя полученные выражения в формулы (3), имеем:
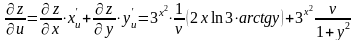 ,
,
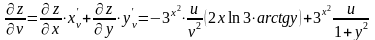 .
.
Ответ можно оставить в такой форме или выразить через u и v. В результате получим:
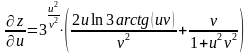 ,
,
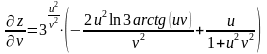 .
.
Инвариантность формы полного дифференциала.
Отметим важное свойство инвариантности формы полного дифференциала. Во всех рассматриваемых выше случаях справедлива формула:
. (*)
Действительно,
дифференциал сложной функции
,
где переменные
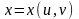 ,
,
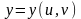 есть функции от новых независимых
переменных u
и v,
можно получить, если в формуле (*)
дифференциалы dx
и dy
заменить (по определению):
есть функции от новых независимых
переменных u
и v,
можно получить, если в формуле (*)
дифференциалы dx
и dy
заменить (по определению):
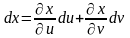 ;
;
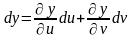 .
.
В результате подстановки и перегруппировки членов при du и dv получим:
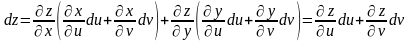 ,
,
где , ,
полученная
формула
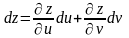 показывает, что форма
первого дифференциала не зависит от
того, являются ли
x
и y
независимыми
переменными или функциями
других независимых переменных. Это
свойство называется инвариантностью
(неизменяемостью) формы
первого дифференциала.
показывает, что форма
первого дифференциала не зависит от
того, являются ли
x
и y
независимыми
переменными или функциями
других независимых переменных. Это
свойство называется инвариантностью
(неизменяемостью) формы
первого дифференциала.
7. Производная по направлению. Градиент функции и его свойство
1.
Производной
от функции
в точке
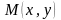 по данному
направлению
вектора
по данному
направлению
вектора
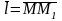 называется
называется
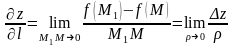 ,
где
,
,
где
,
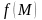 и
и
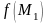 -
значения функции в точках М
и М1.
Если функция
-
значения функции в точках М
и М1.
Если функция
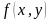 дифференцируема, то производная
дифференцируема, то производная
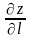 (по направлению
(по направлению
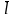 )
вычисляется по формуле:
)
вычисляется по формуле:
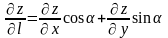 ,
,
где
α- угол, образованный вектором
с осью ОХ. В случае функции трёх переменных
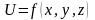 производная по направлению
определяется аналогично и вычисляется
по формуле
производная по направлению
определяется аналогично и вычисляется
по формуле
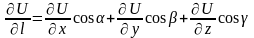 ,
где
,
где
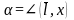 ,
,
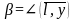 ,
,
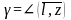 , т.е. α,β,
, т.е. α,β,
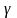 -углы
между направлением
и соответствующими координатными осями,
а
-углы
между направлением
и соответствующими координатными осями,
а
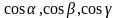 -
направляющие косинусы вектора
,
причём
-
направляющие косинусы вектора
,
причём
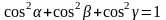 .
Производная
от функции в данном направлении
характеризует скорость изменения
функции в этом направлении.
Производная
.
Производная
от функции в данном направлении
характеризует скорость изменения
функции в этом направлении.
Производная
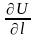 равна нулю по любому направлению,
касательному к поверхности уровня .
Производная
достигает своего наибольшего
значения по направлению нормали (см.
п. 6) к поверхности уровня.
равна нулю по любому направлению,
касательному к поверхности уровня .
Производная
достигает своего наибольшего
значения по направлению нормали (см.
п. 6) к поверхности уровня.
Пример.
Найти производную функции
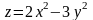 в точке М(1;0) по направлению, составляющему
с ОХ угол в
в точке М(1;0) по направлению, составляющему
с ОХ угол в
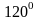 .
.
Решение.
Найдём частные производные и их значения
в данной точке М:
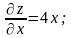
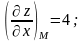
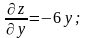
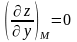 .
.
Далее
определяем
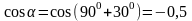 ,
,
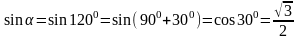 .
.
Применяя
формулу (1), получим искомую производную
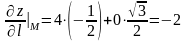 .
Знак минус показывает, что функция в
данной точке по данному направлению
убывает. Известно, что направляющие
косинусы вектора
.
Знак минус показывает, что функция в
данной точке по данному направлению
убывает. Известно, что направляющие
косинусы вектора
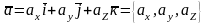 находятся по формулам
находятся по формулам
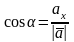 ;
;
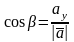 ;
;
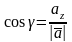 , где
, где
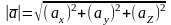
2.
Градиентом
функции
в точке
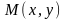 называется вектор, выходящий из точки
М
и имеющей своими координатами частные
производные функции, т.е.
называется вектор, выходящий из точки
М
и имеющей своими координатами частные
производные функции, т.е.
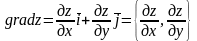 .
На основании этого определения проекции
вектора
.
На основании этого определения проекции
вектора
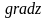 на координатной оси записывается так:
на координатной оси записывается так:
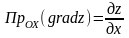 ,
,
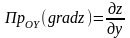 .
Предполагается при этом, что функция
-однозначная
непрерывная, имеющая непрерывные частные
производные, т.е. дифференцируемая.
Значит, производная данной функции в
направлении
связана с градиентом функции следующей
формулой:
.
Предполагается при этом, что функция
-однозначная
непрерывная, имеющая непрерывные частные
производные, т.е. дифференцируемая.
Значит, производная данной функции в
направлении
связана с градиентом функции следующей
формулой:
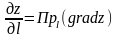 ,
т.е. производная
в данном направлении равна проекции
градиента функции на направление
дифференцирования. Градиент
функции двух переменных в каждой точке
направлен по нормали к соответствующей
линии уровня
функции . Значит направление вектора
в
каждой точке есть направление наибольшей
скорости возрастания функции в этой
точке, т.е. при
,
т.е. производная
в данном направлении равна проекции
градиента функции на направление
дифференцирования. Градиент
функции двух переменных в каждой точке
направлен по нормали к соответствующей
линии уровня
функции . Значит направление вектора
в
каждой точке есть направление наибольшей
скорости возрастания функции в этой
точке, т.е. при
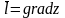 производная
производная
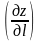 принимает наибольшее значение, равное
модулю вектора
,
т.е.
принимает наибольшее значение, равное
модулю вектора
,
т.е.
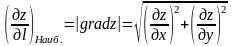 ,
при
.
В этом состоит основное
свойство градиента: градиент указывает
направление наибольшего роста функции
в данной точке.
,
при
.
В этом состоит основное
свойство градиента: градиент указывает
направление наибольшего роста функции
в данной точке.
Он
равен
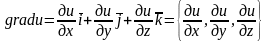 .
Градиент функции трёх переменных в
каждой точке направлен по
нормали к поверхности уровня,
проходящей через эту точку.
.
Градиент функции трёх переменных в
каждой точке направлен по
нормали к поверхности уровня,
проходящей через эту точку.
