
- •Часть 2
- •( Кафедра «высшей математики и физико-математического моделирования») методические указания
- •Часть 2
- •Введение
- •1. Неопределенный интеграл
- •2. Определенный интеграл и его приложения
- •3. Несобственные интегралы
- •2) Вычисление объёмов тел по известным поперечным сечениям
- •1. Функции нескольких переменных Основные теоретические сведения
- •6. Дифференцирование сложной функции
- •7. Производная по направлению. Градиент функции и его свойство
- •8. Производные и дифференциалы высших порядков
- •9. Дифференцирование неявных функций.
- •Касательная плоскость и нормаль к поверхности
- •8. Формула Тейлора для функции двух переменных
- •12. Экстремум функции нескольких независимых переменных
- •13. Условный экстремум. Наибольшее и наименьшее значения функции в замкнутой области
- •14. Дифференциальные уравнения
- •15. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •16. Система линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •Заключение
- •Библиографический список
- •Часть 2
- •Федотенко Галина Федоровна в авторской редакции
16. Система линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
Рассмотрим систему дифференциальных уравнений вида
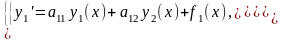
где
f1(x)и
f2(x)-непрерывные
функции. Система называется однородной,
если f1(x)=0,
f2(x)=0,
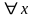 .
Решением системы называется вектор-функция
.
Решением системы называется вектор-функция
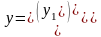 ,
координатные функции которой для всех
х удовлетворяют каждому из равенств.
Задача Коши для системы формируется
следующим образом: найти решение y=y(x)
системы, которые при х=х0
удовлетворяют условиям y1(x0)=y10,
y2(x0)=y20,
где y10
и y20-заданные
числа. Если ввести векторы у,
f(x)=
,
координатные функции которой для всех
х удовлетворяют каждому из равенств.
Задача Коши для системы формируется
следующим образом: найти решение y=y(x)
системы, которые при х=х0
удовлетворяют условиям y1(x0)=y10,
y2(x0)=y20,
где y10
и y20-заданные
числа. Если ввести векторы у,
f(x)=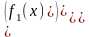 и матрицу
и матрицу
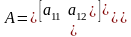 ,
то систему можно записать в матричном
виде
,
то систему можно записать в матричном
виде
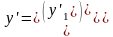
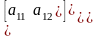
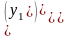 =Ay+f(x).
Вектор-функция
=Ay+f(x).
Вектор-функция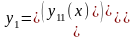 и
и
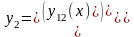 называются линейно независимыми, если
существуют числа
называются линейно независимыми, если
существуют числа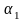 и
и
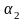 ,
такие что
,
такие что
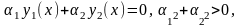 и
линейно независимыми, если основное
тождество выполняется в единственном
случае, когда
и
линейно независимыми, если основное
тождество выполняется в единственном
случае, когда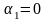 и
и
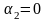 .
Фундаментальной системой решений
однородной системы
.
Фундаментальной системой решений
однородной системы
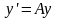 называется два ее линейно независимых
решения
,
.
Общим решением системы
называется решение
называется два ее линейно независимых
решения
,
.
Общим решением системы
называется решение
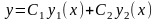 ,
где С1
и С2
– произвольные постоянные, у1,
у 2
–фундаментальная система решений.
Частным решением у0
системы (40) называется любое решение,
удовлетворяющее ей. Общим решением
неоднородной системы является
вектор-функция
,
где С1
и С2
– произвольные постоянные, у1,
у 2
–фундаментальная система решений.
Частным решением у0
системы (40) называется любое решение,
удовлетворяющее ей. Общим решением
неоднородной системы является
вектор-функция
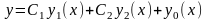 ,
где
,
-
фундаментальная система,
,
где
,
-
фундаментальная система,
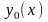 -
частное решение.
-
частное решение.
Решение задач
Задача 1.
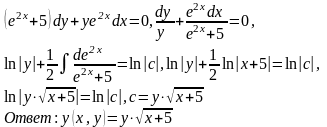
Задача 2.
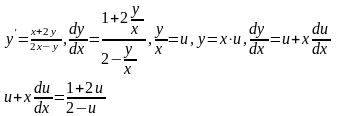 ,
,
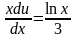 ,
,
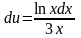 ,
,
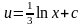 ,
,
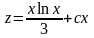 ,
,
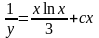 -общее
решение,
-общее
решение,
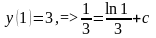 ,
,
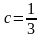 ,
,
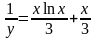 ,
,
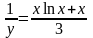 ,
,
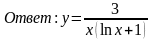 .
.
Задача 3.
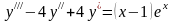
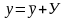 ,
,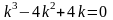 -
характеристическое ур-е
-
характеристическое ур-е
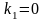 ,
,
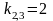 ,
,
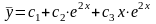 - общее
решение однородного уравнения
- общее
решение однородного уравнения
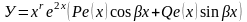
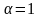 ,
,
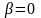 ,
,
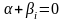 ,
,
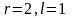
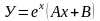 ,
,
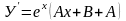
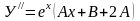 ,
,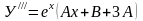
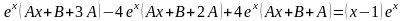 ,
,
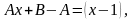
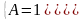
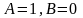 ,
,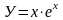 ,
,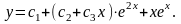
Ответ:
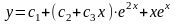
Задача 4
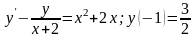
Решим однородное уравнение, соответствующее данному неоднородному:
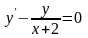 ,
,
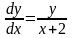 ,
,
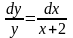
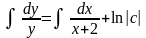 ,
,
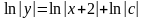
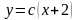
Используя метод вариации произвольных постоянных, найдём частное решение искомого уравнения ,а затем общее:
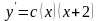 ,
,
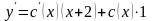 ,
,
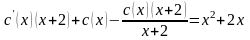 ,
,
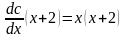 ,
,
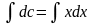
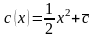 ,
,
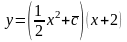 - общее решение.
- общее решение.
Найдём
частное решение
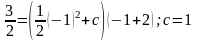 .
.
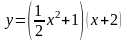 -
частное решение. Ответ:
-
частное решение. Ответ:
Задача 5.
Найти решение задачи Коши.
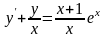 ,
,
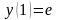 ,
,
,
,
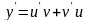
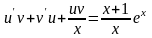 ,
,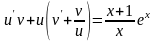
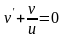 ,
,
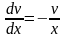 ,
,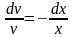 ,
,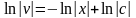
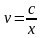 ,
,
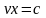 ,
,
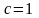 ,
,
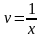 ,
,
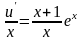 ,
,
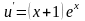
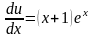 ,
,
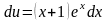 ,
,
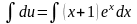
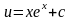 ,
,
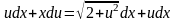 ,
,
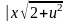 ,
,
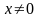 .
.
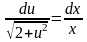 ,
,
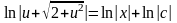 ,
,
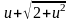
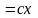
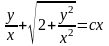 ,
,
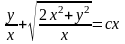 ,
,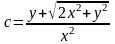
Ответ:
Задача 6.
Найти общий интеграл
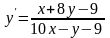 ,
,
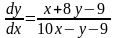 ,
,
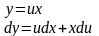
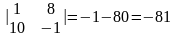 ,
,
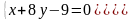 ,
,
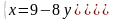 .
.
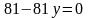 ,
,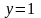 ,
,
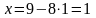 ,
,
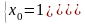 ,
,
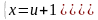 .
.
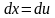 .
.
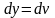 ,
,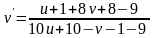 ,
,
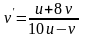 ,
,
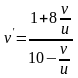 .
.
Делаем
замену
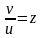 ,
,
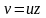 ,
,
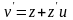 ,
,
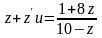 ,
,
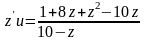 и
и
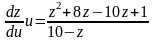 ,
,
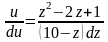 ,
,
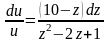 ,
,
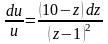 и
и
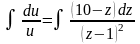 т.е.
т.е.
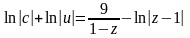 ,
,
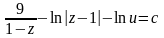 ,
,
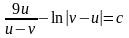 .
.
Ответ:
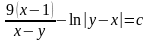
Задача 7.
Найти решение задачи Коши.
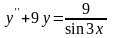 ,
,
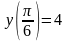 ,
,
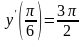 .
.
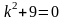 ,
,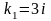 ,
,
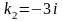 .
.
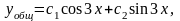
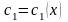 ,
,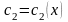 .
.
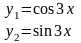 ,
,
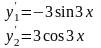 .
.
Пусть
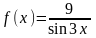 .
.
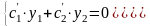 ,
,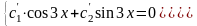
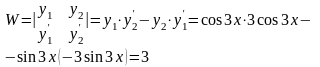
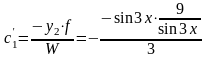 ,
,
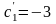 ,
,
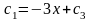 .
.
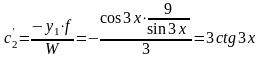 ,
,
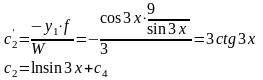 ,
,
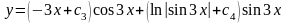 .
.
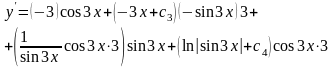
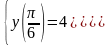 ,
,
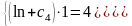 ,
,
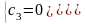 .
.
Ответ:
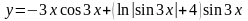
Задача 8.
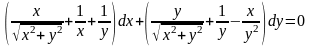
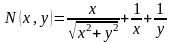
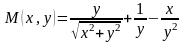
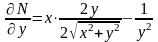 ,
,
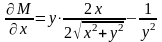
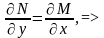 данное
уравнение в полных дифференциалах
данное
уравнение в полных дифференциалах
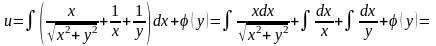
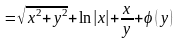 .
.
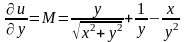
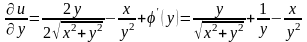 ,
,
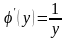 ,
,
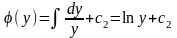 ,
,
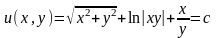
Ответ:
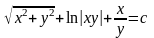
Задача 9.
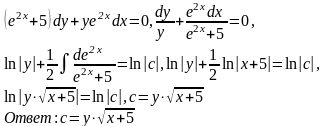
Задача 10.
Решить дифференциальное уравнение
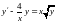 .
.
Это уравнение Бернулли с
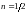 .
Полагаем
.
Полагаем
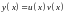 .
Получаем уравнение
.
Получаем уравнение
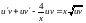 или
или
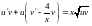 .
Подберем такую функцию
.
Подберем такую функцию
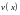 ,
чтобы выражение в скобках было равно
нулю, т.е. решим дифференциальное
уравнение
,
чтобы выражение в скобках было равно
нулю, т.е. решим дифференциальное
уравнение
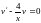 .
Находим
.
Находим
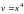 .
Решаем затем уравнение
.
Решаем затем уравнение
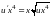 и получаем его общее решение
и получаем его общее решение
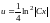 .
Следовательно, общее решение исходного
уравнения
.
Следовательно, общее решение исходного
уравнения
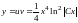 .
Нетрудно заметить, что
.
Нетрудно заметить, что
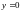 является особым решение исходного
уравнения.
является особым решение исходного
уравнения.
Ответ: y=
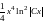 .
.
Задача 11.
Решить
систему
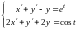 при данных начальных условиях:
при данных начальных условиях:
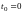 ,
,
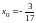 ,
,
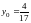 .
.
Сначала приводим систему к нормальному виду
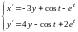 .
.
Первое
уравнение дифференцируем по
 ,
после чего вместо
,
после чего вместо
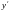 подставим выражение из второго уравнения
системы:
подставим выражение из второго уравнения
системы:
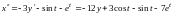 .
Из этого уравнения и первого уравнения
исходной системы составим новую систему
.
Из этого уравнения и первого уравнения
исходной системы составим новую систему
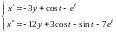 , из первого уравнения которой выражаем
, из первого уравнения которой выражаем
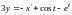 и, подставляя во второе, получаем
и, подставляя во второе, получаем
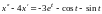 .
Соответствующее характеристическое
уравнение
.
Соответствующее характеристическое
уравнение
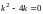 имеет корни
имеет корни
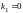 ,
,
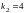
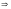
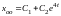 .
Частное решение ищем в виде
.
Частное решение ищем в виде
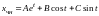 .
После определения коэффициентов получаем
.
После определения коэффициентов получаем
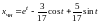 .
Следовательно
.
Следовательно
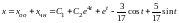 .
Найдя производную
.
Найдя производную
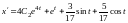 ,
получаем
,
получаем
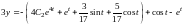 .
Таким образом, общее решение исходной
системы имеет вид
.
Таким образом, общее решение исходной
системы имеет вид
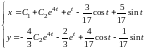 .
.
Подставляя
начальные условия, определяем значения
постоянных
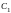 и
и
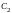 :
:
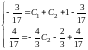
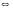
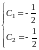 .
.
Итак, мы имеем ответ.
Ответ: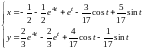 .
.
