- •Часть 2
- •( Кафедра «высшей математики и физико-математического моделирования») методические указания
- •Часть 2
- •Введение
- •1. Неопределенный интеграл
- •2. Определенный интеграл и его приложения
- •3. Несобственные интегралы
- •2) Вычисление объёмов тел по известным поперечным сечениям
- •1. Функции нескольких переменных Основные теоретические сведения
- •6. Дифференцирование сложной функции
- •7. Производная по направлению. Градиент функции и его свойство
- •8. Производные и дифференциалы высших порядков
- •9. Дифференцирование неявных функций.
- •Касательная плоскость и нормаль к поверхности
- •8. Формула Тейлора для функции двух переменных
- •12. Экстремум функции нескольких независимых переменных
- •13. Условный экстремум. Наибольшее и наименьшее значения функции в замкнутой области
- •14. Дифференциальные уравнения
- •15. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •16. Система линейных дифференциальных уравнений второго порядка с постоянными коэффициентами
- •Заключение
- •Библиографический список
- •Часть 2
- •Федотенко Галина Федоровна в авторской редакции
15. Линейные дифференциальные уравнения второго порядка с постоянными коэффициентами
Линейным дифференциальным уравнением второго
порядка с постоянными коэффициентам называется
уравнение
вида
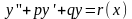 ,
где p,
q-
некоторые числа; r(x)-функция
от х.
,
где p,
q-
некоторые числа; r(x)-функция
от х.
Однородным линейным дифференциальным уравнением второго порядка с постоянными коэффициентами называется уравнение, в котором правая часть r(х) равна нулю:
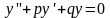 .
Общее решение уравнения равно сумме
какого либо частного решения этого
уравнения и общего
.
Общее решение уравнения равно сумме
какого либо частного решения этого
уравнения и общего
решения соответствующего однородного уравнения . Опишем сначала способ нахождения общего решения однородного уравнения . Характеристическим уравнением для однородного
уравнения
называется квадратное уравнение
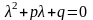
Относительно неизвестной . В соответствии со знаком дискриминанта D=p2-4q возможны три случая:
D>0: характеристическое уравнение имеет два
различных
корня
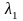 и
и
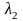 ;
;
D=0: характеристическое уравнение имеет один
корень
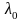 ;
;
D<0: действительных корней характеристическое
Уравнение не имеет. В этом случае находятся числа
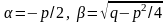 .
.
Найдем решение уравнения для всех этих случает.
Если характеристическое уравнение имеет
два
различных корня
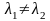 ,
то общее решение уравнения имеет вид
,
то общее решение уравнения имеет вид
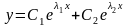 ,
где С1,
С2
,
где С1,
С2—произвольные
постоянные.
Если характеристическое уравнение имеет единственный корень , то общее решение уравнения имеет вид
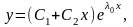 где
С1,
С2
где
С1,
С2—произвольные
постоянные.
Характеристическое уравнение не имеет корней, то общее решение уравнения имеет вид
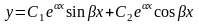 ,
,
где
С1,
С2—произвольные
постоянные, где
.
Способы нахождения частных решений
неоднородного уравнения зависят от
вида правой части и в явном виде находятся
только для функций f(x)
специального вида.
Пусть
f(x)
имеет вид
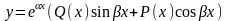 ,
,
где
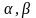 -
некоторые числа, причем
-
некоторые числа, причем
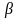 не равно нулю, Q(x),
P(x)-многочлены
от х. В этом случае частное решение
уравнения ищется в виде
не равно нулю, Q(x),
P(x)-многочлены
от х. В этом случае частное решение
уравнения ищется в виде
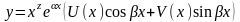 ,
,
где U(x),V(x)-многочлены, степени которых равны наибольшей из степеней многочленов P(x) и Q(x). При этом показатель s выбирается по следующему правилу:
z=0, если
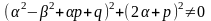 ;
;
z=1,
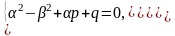
Многочлены U(x) и V(x) указанной степени в формуле записываются в общем виде с произвольными коэффициентами. Затем находится производные y’ и y’’ функции . После подстановки y, y’ и y’’ в уравнение получается линейная система уравнений для определения коэффициентов многочленов U(x) и V(x). Пусть теперь правая часть уравнения имеет вид
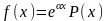 ,
где
-некоторое
число, Р(х)- многочлен от х Частное решение
уравнения ищется в виде
,
где
-некоторое
число, Р(х)- многочлен от х Частное решение
уравнения ищется в виде
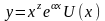 ,
,
где U(x)-многочлен с неопределенными коэффициентами,
степень которого равна степени многочлена Р(х). При этом
показатель z выбирается по следующему правилу:
Z=0, если
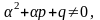
Z=1,
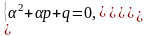 3)
Z=2,
3)
Z=2,
Линейные дифференциальные уравнения второго
порядка с переменными коэффициентами.
Уравнение
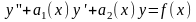
Представляет
собой общий вид дифференциального
уравнения второго порядка с правой
частью f(x).
Здесь
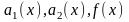 -некоторые
непрерывные функции.
-некоторые
непрерывные функции.
Уравнение называется однородным, если f(x)=0.
Задачей
Коши называется задача решения уравнения
при заданных начальных условиях
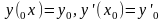 .
Линейными независимыми решениями
однородного уравнения
.
Линейными независимыми решениями
однородного уравнения
называется
решение
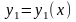 ,
,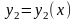 ,
для которого
,
для которого
определитель Вронского (вронскиан)
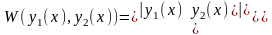 ,
,
И
линейно зависимыми, если
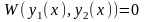 для некоторых х. Известно, что всякое
линейное уравнение однородное уравнение
для некоторых х. Известно, что всякое
линейное уравнение однородное уравнение
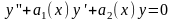 ,
где
,
где
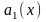 и
и
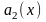 -
непрерывные функции, имеет два линейно
независимых решения. Фундаментальной
системой решений называется система
двух линейно независимых функций
-
непрерывные функции, имеет два линейно
независимых решения. Фундаментальной
системой решений называется система
двух линейно независимых функций
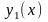 и
и
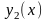 ,
являющихся решениями однородного
уравнения. Для решений уравнений вида
применяется метод вариации произвольных
постоянных, который заключатся в том,
что общее решения уравнения ищется в
виде
,
являющихся решениями однородного
уравнения. Для решений уравнений вида
применяется метод вариации произвольных
постоянных, который заключатся в том,
что общее решения уравнения ищется в
виде
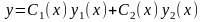 ,
где
,
где
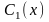 и
и
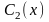 -функции,
которые определяются из системы уравнений
-функции,
которые определяются из системы уравнений
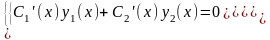 .
Из системы находится
.
Из системы находится
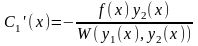 ,
,
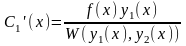 .
Тогда
.
Тогда