
- •Часть 1
- •(Кафедра «высшей математики и физико-математического моделирования») методические указания
- •Часть 1
- •Введение
- •1. Линейные пространства. Разложение векторов по базису
- •2. Решение систем линейных уравнений
- •3. Подпространства, образованные решениями линейной однородной системы (лос) уравнений. Нахождение общего решения лос
- •4. Линейные преобразования и действия Над ними
- •5. Собственные значения и собственные векторы матрицы
- •6. Приведение квадратичной формы к каноническому виду
- •7. Векторы и действия над ними
- •8. Плоскость и прямая в пространстве
- •10. Приведение общего уравнения кривой второго порядка к каноническому виду
- •11. Исследование общего уравнения кривой
- •Числовая последовательность и ее предел
- •13. Предел функции
- •14. Применение эквивалентных бесконечно малых к вычислению пределов
- •15. Первый замечательный предел
- •16. Вычисление предела показательно-степенной функции
- •17. Производная функции и ее вычисление
- •18. Производная сложной функции.
- •19. Дифференциал функции. Применение дифференциала
- •20. Логарифмическая производная
- •21. Дифференцирование функций, заданных параметрически
- •22. Производные высших порядков. Формула Лейбница
- •23. Возрастание и убывание функции. Локальный экстремум функции
- •Достаточные условия существования и отсутствия экстремума непрерывной функции :
- •24. Асимптоты
- •25. Направление выпуклости кривой. Точки перегиба
- •26. Общая схема полного исследованфункции и построение графика функции
- •Заключение
- •Библиографический список
- •Часть 1
- •Федотенко Галина Федоровна в авторской редакции
4. Линейные преобразования и действия Над ними
Говорят,
в линейном векторном пространстве R
задано преобразование А,
если каждому элементу (вектору)
 по некоторому закону (или правилу)
ставится в соответствие вектор
по некоторому закону (или правилу)
ставится в соответствие вектор
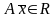 . Преобразование А
называют
линейным , если для любых векторов
. Преобразование А
называют
линейным , если для любых векторов
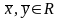 и любого действительного числа
и любого действительного числа
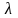 выполняется
равенства
выполняется
равенства
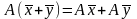 и
и
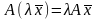 .
.
Для простоты возьмём линейное пространство R3 (n=3) .
Пусть
в этом пространстве R3
имеются два базиса:
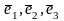
(старый)
и
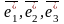 (новый), связанные равенствами
(новый), связанные равенствами
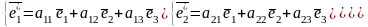 (**)
(**)
где
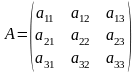 матрица перехода от старого базиса к
новому, столбцы, которой являются
координатами в формулах перехода (**).
матрица перехода от старого базиса к
новому, столбцы, которой являются
координатами в формулах перехода (**).
Если
вектор
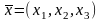 задан в базисе
,
то его координаты
задан в базисе
,
то его координаты
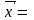
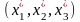 в новом базисе можно найти по формуле
в новом базисе можно найти по формуле
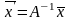 ,
где матрица линейного преобразования
,
где матрица линейного преобразования
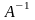 является
обратной для матрицы A;
т.к. detA
является
обратной для матрицы A;
т.к. detA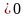 ,то - невырожденная матрица. Заметим,
что в конечномерном пространстве R
линейное преобразование (оператор)
называется невырожденным , если
определитель матрицы этого линейного
преобразования отличен от нуля. Матрицу
,то - невырожденная матрица. Заметим,
что в конечномерном пространстве R
линейное преобразование (оператор)
называется невырожденным , если
определитель матрицы этого линейного
преобразования отличен от нуля. Матрицу
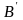 линейного оператора (преобразования )
при переходе от одного ортонормированного
базиса к другому находится по формуле
линейного оператора (преобразования )
при переходе от одного ортонормированного
базиса к другому находится по формуле
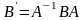 ,
где A-матрица
перехода от старого базиса к новому , B
матрица оператора в старом базисе
,
где A-матрица
перехода от старого базиса к новому , B
матрица оператора в старом базисе
Пример. Найти координаты вектора в базисе
( ), если он задан в базисе ( ).
Дано:
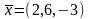 ,
,
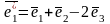 ,
,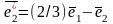 ,
,
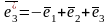
Решение.
Имеем по условию разложение вектора
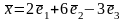 старом
базисе
.
Требуется разложить вектор
в новом базисе
,
т.е. надо найти новые координаты
старом
базисе
.
Требуется разложить вектор
в новом базисе
,
т.е. надо найти новые координаты
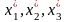 вектора
вектора
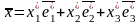 .
Учитывая
условие задачи, запишем
.
Учитывая
условие задачи, запишем
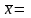
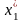
 +
+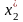
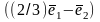 +
+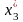
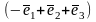 или в
координатной форме
или в
координатной форме
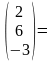
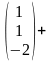

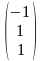
Векторное
уравнение равносильно трем скалярным
уравнениям :
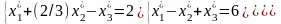
Это линейная неоднородная система(ЛНС), у которой
det A=-1. Решаем ЛНС уравнений по правилу Крамера:
 ,
,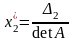 ,
,
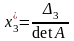
Находим:
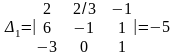 ,
,
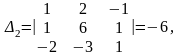
 .
.
Получим
=5,
=6,
=7.
Таким образом,
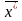 =(5,6,7).
=(5,6,7).
5. Собственные значения и собственные векторы матрицы
Пусть Rn - заданное n-мерное линейное пространство .
Ненулевой
вектор
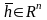 называется собственным вектором
линейного оператора (преобразования)
,заданного матрицей А
, если найдется такое число
,
что выполняется равенство
называется собственным вектором
линейного оператора (преобразования)
,заданного матрицей А
, если найдется такое число
,
что выполняется равенство
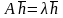 .Само
число
называют
собственным (или характеристическим)
числом оператора А,
соответствующим собственному вектору
.Само
число
называют
собственным (или характеристическим)
числом оператора А,
соответствующим собственному вектору
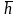 .
Собственные (значения) матрицы А
являются корнями характеристического
уравнения det
(A-
E)=0,
являющегося алгебраическим уравнением
n-ой
степени.
.
Собственные (значения) матрицы А
являются корнями характеристического
уравнения det
(A-
E)=0,
являющегося алгебраическим уравнением
n-ой
степени.
Если
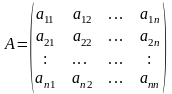 ,
,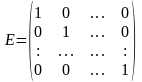 ,
,
то характеристическое уравнение в координатной форме имеет вид:
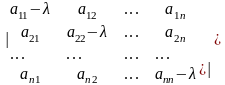 =0
(***)
=0
(***)
Для нахождения ненулевого собственного вектора
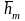 =
=
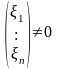 ,
отвечающему собственному числу
,
отвечающему собственному числу
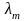 ,
,
m=1,2,…n надо решить линейную однородную систему (ЛОС) уравнений:
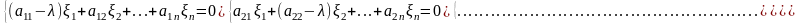
Эта ЛОС уравнений имеет бесконечно много решений. Поэтому, собственному значению соответствует семейство собственных векторов. Выбирают любой из них.
Если
характеристическое уравнение (***) имеет
n
различных корней, то соответствующие
им собственные векторы
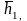
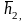 …
…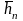 -
линейно независимые и образуют базис.
Если среди корней характеристического
уравнения (*) имеются кратные, т.е. равные
корни, например,
-
линейно независимые и образуют базис.
Если среди корней характеристического
уравнения (*) имеются кратные, т.е. равные
корни, например,
 -
корень кратности к,
то хорошо найти к
линейно независимых собственных векторов
…
-
корень кратности к,
то хорошо найти к
линейно независимых собственных векторов
…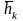 ,
отвечающих собственному значению,
кратности к;
их число m=n-r
, где n-порядок
матрицы
(A-
E),
r=Rang
(A-
E);
,
отвечающих собственному значению,
кратности к;
их число m=n-r
, где n-порядок
матрицы
(A-
E),
r=Rang
(A-
E);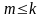 .
.
Пример. Найти собственные значения и собственные векторы матрицы А.
Дано:
 .
.
Решение.
Составляем и решаем характеристическое
уравнение
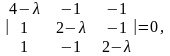
 ,
или
,
или
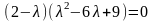 ,
,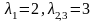 .
.
Откуда -собственные значения матрицы А.
Для
простого корня
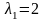 находим собственный вектор
=
находим собственный вектор
=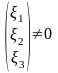 ,
решая ЛОС уравнений
,
решая ЛОС уравнений
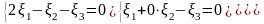 ,коэффициенты
этой системы равны элементам определителя
det (A-
E)=0,
при
:
,коэффициенты
этой системы равны элементам определителя
det (A-
E)=0,
при
:

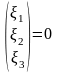 .Решим
методом Гаусса, исключая неизвестные:
.Решим
методом Гаусса, исключая неизвестные:
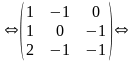
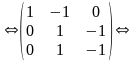
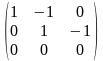 , получим
, получим
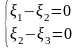 или
или
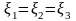 ,
где
,
где
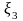 -свободная переменная , полагая
-свободная переменная , полагая
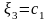 ,
получаем,
,
получаем,
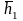 =
=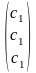 -семейство собственных векторов,
отвечающих собственному значению
.
Например,
=
-семейство собственных векторов,
отвечающих собственному значению
.
Например,
=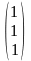 .
Для кратного корня
.
Для кратного корня
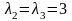 сначала определим число линейно
независимых собственных векторов.
Подставляя
сначала определим число линейно
независимых собственных векторов.
Подставляя
 в левую часть характеристического
уравнения, получаем матрицу
в левую часть характеристического
уравнения, получаем матрицу
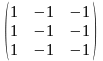 .
.
Ее порядок n=3 , ранг r=1 (наивысший порядок миноров , не равных нулю). Число линейно независимых собственных векторов равно m=n-r=2 и совпадает с кратностью корня к=2 .Найдем их.
Имеем
 или
или
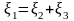 .Полагая
.Полагая
 где
где -любые
константы, одновременно не обращающееся
в ноль, получим
=
-любые
константы, одновременно не обращающееся
в ноль, получим
=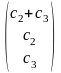 -
семейство собственных векторов для
.
Пусть
-
семейство собственных векторов для
.
Пусть
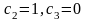 .
Тогда
.
Тогда
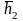 =
=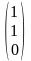 .
Пусть
.
Пусть
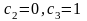 .
Тогда
.
Тогда
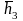 =
=
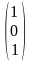 .
.
Два линейно независимых собственных вектора и , соответствующих собственному числу .
Ответ: , – собственные значения
матрицы
A,
 ,
,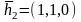 ,
,
