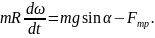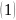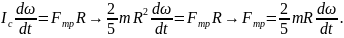- •Основные законы механики в примерах и задачах методические указания
- •Предисловие
- •1. Кинематика точки и твердого тела
- •2. Динамика материальной точки и твердого тела
- •3. Упругие деформации тел
- •4. Механические колебания и упругие волны
- •5. Релятивистская механика
- •6. Механика жидкости
- •Библиографический список
- •5. Сборник задач по общему курсу физики ( механике) [Текст] / под ред. И.А. Яковлева. – м. : Наука., физ. – мат. Лит., 1977. – 288 с.
- •Основные законы механики в примерах и задачах методические указания
- •394026 Воронеж, Московский просп., 14
2. Динамика материальной точки и твердого тела
2.1. Шарик массы m помещен в высокий сосуд с некоторой жидкостью и отпущен без толчка. Плотность жидкости в n раз меньше плотности шарика. При движении шарика возникает сила сопротивления среды, пропорциональная скорости движения: F = — kV.
а) Описать качественно характер движения шарика.
б) Найти зависимость скорости шарика V от времени t.
Решение.
На
падающий в жидкости шарик действует
три силы — тяжести, Архимеда и
сопротивления. Уравнение движения
шарика имеет вид
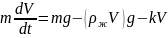 (1), где
(1), где
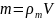 — масса шарика, V
— его объем;
— масса шарика, V
— его объем;
 и
и
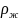 — плотности тела и жидкости. Равенство
(1) поделим на m
и учтем, что
— плотности тела и жидкости. Равенство
(1) поделим на m
и учтем, что
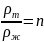 .
При этом уравнение (1) получит вид
.
При этом уравнение (1) получит вид
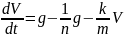 ,
или
,
или
 ,
,
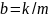 .
Отсюда путем интегрирования получим:
.
Отсюда путем интегрирования получим:
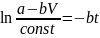 =>
=>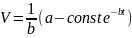 .
Из начального условия
.
Из начального условия
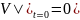 следует, что const
= a
и затем
следует, что const
= a
и затем
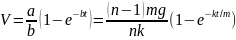 .
.
2.2. Тонкая стальная цепочка с очень мелким звеньями висит вертикально, касаясь нижним концом стола. Масса цепочки m, длина L. В момент t = 0 цепочку отпускают. Считая цепочку однородной по длине, найти:
а) мгновенное значение силы F(t), с которой цепочка действует на стол;
б) среднее значение <F> этой силы за время падения.
Р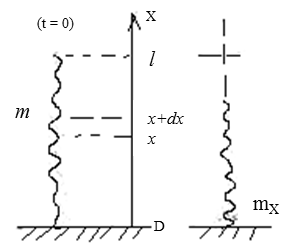 ешение.
Предварительно
отметим: при растяжении цепочки между
ее звеньями возникают упругие силы; при
падении в поле тяжести звенья не
взаимодействуют, каждое звено падает
с ускорение
ешение.
Предварительно
отметим: при растяжении цепочки между
ее звеньями возникают упругие силы; при
падении в поле тяжести звенья не
взаимодействуют, каждое звено падает
с ускорение
 независимо друг от друга. Согласно
условиям, сила действия цепочки на стол
в начале падения равна нулю, в конце
падения эта сила получает максимальное
значение 3mg.
Обратимся к рисунку и сделаем следующие
вычисления. Элементы цепочки, падая с
высоты х, независимо от других элементов
приобретают скорость V
= gt
и соответствующий импульс
независимо друг от друга. Согласно
условиям, сила действия цепочки на стол
в начале падения равна нулю, в конце
падения эта сила получает максимальное
значение 3mg.
Обратимся к рисунку и сделаем следующие
вычисления. Элементы цепочки, падая с
высоты х, независимо от других элементов
приобретают скорость V
= gt
и соответствующий импульс
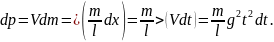 При падении элемент цепочки действует
на поверхность стола силой
При падении элемент цепочки действует
на поверхность стола силой
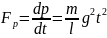 .
Помимо этой силы на поверхность стола
действует сила тяжести упавшей части
цепочки к моменту времени t,
равная
.
Помимо этой силы на поверхность стола
действует сила тяжести упавшей части
цепочки к моменту времени t,
равная
 Суммарная сила
Суммарная сила
 Итак,
Итак,
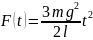 .
Средняя сила
.
Средняя сила
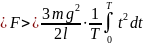 ,
где T
— время падения цепочки. Таким образом,
,
где T
— время падения цепочки. Таким образом,
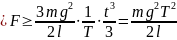 .
Поскольку
.
Поскольку
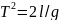 ,
то <F>
= mg.
,
то <F>
= mg.
2.3.
Тело массы m
начинает двигаться под действием силы
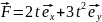 .
Найти мощность P(t),
развиваемую силой в момент времени t.
.
Найти мощность P(t),
развиваемую силой в момент времени t.
Решение.
Мощность
P
силы
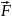 вычислим по формуле P
=
вычислим по формуле P
=
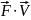 ,
где
— скорость поступательного движения
тела. В рассматриваемом случае
.
Отсюда ускорение и скорость тела:
,
где
— скорость поступательного движения
тела. В рассматриваемом случае
.
Отсюда ускорение и скорость тела:
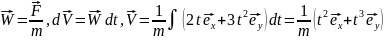 .
Начальные условия: при t
= 0 величины F,
и
равны нулю. Мощность силы
.
Начальные условия: при t
= 0 величины F,
и
равны нулю. Мощность силы
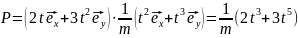 .
.
2.4. Небольшое тело начинает скользить без трения с вершины сферы радиуса R вниз. На какой высоте h над центром сферы тело отделится от поверхности сферы и полетит свободно?
Р ешение.
На
рисунке изображены сила тяжести тела
ешение.
На
рисунке изображены сила тяжести тела
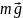 и сила нормальной реакции
и сила нормальной реакции
 .
Трения скольжения нет. Центростремительная
сила, действующая на тело, равна
.
Трения скольжения нет. Центростремительная
сила, действующая на тело, равна
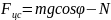 .
При отрыве тела от поверхности сферы N
= 0 и
.
При отрыве тела от поверхности сферы N
= 0 и
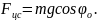 Как известно,
Как известно,
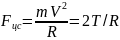 ,
где Т — кинетическая энергия. На основании
закона сохранения механической энергии
тела в потенциальном поле сил тяжести
Т = mg(R
— h).
Таким образом получаем соотношение
,
где Т — кинетическая энергия. На основании
закона сохранения механической энергии
тела в потенциальном поле сил тяжести
Т = mg(R
— h).
Таким образом получаем соотношение
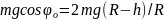 (*). Если учесть, что
(*). Если учесть, что
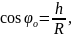 то из (*) найдем: h
= 2(R
— h)
=>h
= (2/3)R.
то из (*) найдем: h
= 2(R
— h)
=>h
= (2/3)R.
2.5.
Потенциальная
энергия частицы имеет вид: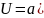 ),
где
),
где
 — константа. Найти:
— константа. Найти:
а) силу F, действующую на частицу,
б) работу А, совершаемую над частицей силами поля при переходе частицы из точки (1, 1, 1) в точку (2, 2, 3)
Решение. Имеется связь между силой и потенциальной энергией частицы в силовом поле, а именно
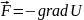
В декартовых координатах
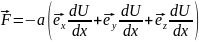
В
рассматриваемом случае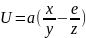 .
.
Поэтому
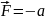 {
{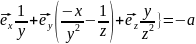 {
{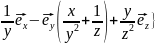
Работа,
совершаемая силами поля при перемещении
частицы из точки
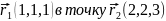 ,
равна
,
равна
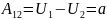 {
{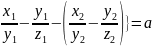 {
{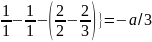 .
.
2.6.
На
столе лежит доска массы
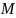 = 1 кг, а на доске – груз массы m = 2 кг.
Какую силу
= 1 кг, а на доске – груз массы m = 2 кг.
Какую силу
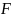 нужно приложить к доске, чтобы доска
выскользнула из-под груза? Коэффициент
трения между грузом и доской 1
= 0,25 , а между доской и столом 2
= 0,5.
нужно приложить к доске, чтобы доска
выскользнула из-под груза? Коэффициент
трения между грузом и доской 1
= 0,25 , а между доской и столом 2
= 0,5.
Р ешение.
Механическая
система с указанием действующих на нее
сил показана на рисунке. Уравнение
движения доски:
ешение.
Механическая
система с указанием действующих на нее
сил показана на рисунке. Уравнение
движения доски:
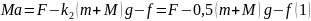
И
уравнение движения груза:
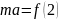 ,где
,где
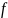 -
сила трения между грузом и доской,
– ускорение.
-
сила трения между грузом и доской,
– ускорение.
Максимальное
значение
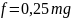 ;
следовательно, максимальное ускорение
груза 0,25
;
следовательно, максимальное ускорение
груза 0,25 ,
и максимальная сила
,
при которой еще будет происходить
движение груза и доски как целого, должна
сообщать доске и грузу ускорение
,
и максимальная сила
,
при которой еще будет происходить
движение груза и доски как целого, должна
сообщать доске и грузу ускорение
 .
А для этого, согласно уравнению (1), сила
должна быть равна
.
А для этого, согласно уравнению (1), сила
должна быть равна

Для m=2кг, =1кг сила =22,5H.
2.7.
Определить
расстояние
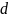 центра масс полуокружности радиуса
центра масс полуокружности радиуса
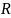 от стягивающего её диаметра.
от стягивающего её диаметра.
Решение.
Ясно,
что центр масс данного полукольца
находится на оси
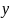 (см.рис.).
Ордината выделенного углом
(см.рис.).
Ордината выделенного углом
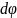 элемента полукольца равна
элемента полукольца равна
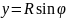 ,
масса этого элемента
,
масса этого элемента
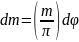 .
Ордината центра масс полукольца равна
.
Ордината центра масс полукольца равна
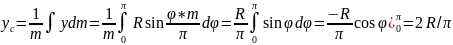
Итак,
координаты центра масс:
2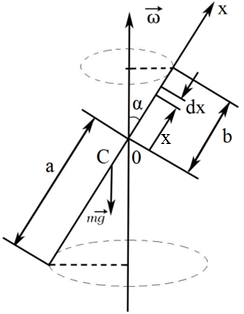 .8.
Тонкий
стержень длиной
.8.
Тонкий
стержень длиной
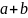 шарнирно
закреплен в точке, отстоящей на расстояние
«b»
от одного из его концов, и вращается с
угловой скоростью
шарнирно
закреплен в точке, отстоящей на расстояние
«b»
от одного из его концов, и вращается с
угловой скоростью
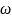 вокруг вертикальной оси, описывая
круговой конус (см. рис.). Определить
угол отклонения стержня от вертикали.
вокруг вертикальной оси, описывая
круговой конус (см. рис.). Определить
угол отклонения стержня от вертикали.
Решение.
В
системе координат, вращающейся вокруг
вертикальной оси с угловой скоростью
,
условие равновесия стержня можно
записать в виде
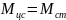 ,
где
,
где
 – момент центробежной силы и
– момент центробежной силы и
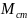 – момент силы тяжести относительно
точки закрепления стержня (шарнира О).
Центробежная сила инерции, действующая
на элемент стержня
– момент силы тяжести относительно
точки закрепления стержня (шарнира О).
Центробежная сила инерции, действующая
на элемент стержня
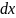 ,
находящийся на расстоянии
,
находящийся на расстоянии
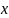 от точки закрепления, будет равна
от точки закрепления, будет равна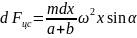 ,
а
соответствующий момент этой силы можно
записать в виде
,
а
соответствующий момент этой силы можно
записать в виде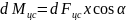 .
.
При этом полный момент центробежной силы инерции равен

Приравнивая
эту величину моменту силы тяжести
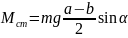 ,
получим:
,
получим:
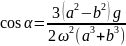
2.9.
На
небольшое тело массы m, лежащее на гладкой
горизонтальной плоскости, в момент
 = 0 начала действовать сила, зависящая
от времени по закону
= 0 начала действовать сила, зависящая
от времени по закону
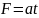 ,
где
,
где
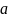 - постоянная. Направление этой силы все
время составляет угол α с горизонтом.
Найти:
- постоянная. Направление этой силы все
время составляет угол α с горизонтом.
Найти:
а) скорость тела в момент отрыва от плоскости;
б) путь, пройденный телом к этому моменту.
Р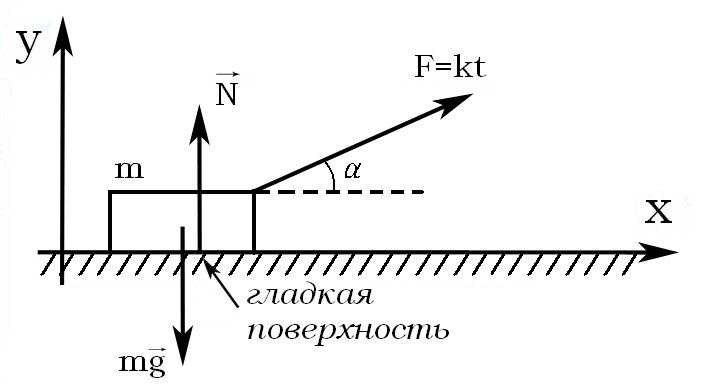 ешение.
ешение.
До
некоторого момента времени
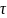 тело движется горизонтально с ускорением
тело движется горизонтально с ускорением
 ,
при этом
,
при этом
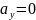 и
и
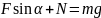 ,
т.е.
,
т.е.
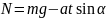 .
В момент отрыва
.
В момент отрыва
 и
и
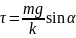 .
.
а)
Скорость тела в момент времени
равна
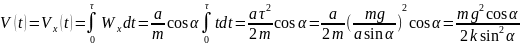
б)
Путь за время
равен
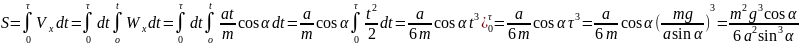 .
.
2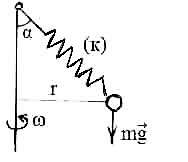 .10.
Шарик
массы m подвешен на идеальной пружине
жесткости k
и начальной длины l
над центром платформы центробежной
машины. Затем шарик начинает вращаться
вместе с машиной с угловой скоростью
ω. Какой угол α образует при этом пружина
с вертикалью?
.10.
Шарик
массы m подвешен на идеальной пружине
жесткости k
и начальной длины l
над центром платформы центробежной
машины. Затем шарик начинает вращаться
вместе с машиной с угловой скоростью
ω. Какой угол α образует при этом пружина
с вертикалью?
Решение.
Данную
механическую систему ещё до вращения
можно рассматривать как колебательную
с двумя степенями свободы, характеризующуюся
двумя частотами
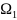 =
=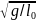 и
и
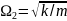 .
Вопросы колебательных движений данной
системы не так просты и мы их опустим.
Будем считать, что в начальный момент
времени система находилась в покое,
колебания не совершались. Далее будем
приводить систему во вращательное
движение до заданной угловой скорости
очень медленно, полагая, что колебания
в системе не возникнут.
.
Вопросы колебательных движений данной
системы не так просты и мы их опустим.
Будем считать, что в начальный момент
времени система находилась в покое,
колебания не совершались. Далее будем
приводить систему во вращательное
движение до заданной угловой скорости
очень медленно, полагая, что колебания
в системе не возникнут.
Для получения ответа на поставленный вопрос перейдем во вращающуюся систему координат, приложив к шарику еще дополнительную центробежную силу инерции. В этой системе координат в принятых условиях шарик будет находиться в состоянии покоя (равновесия).
Пусть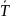 – упругая сила натяжения пружины. По
величине она равна T=k(l-
– упругая сила натяжения пружины. По
величине она равна T=k(l-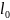 ),
где l
– длина пружины в состоянии растяжения,
– её длина в недеформированном состоянии.
Центробежная сила
),
где l
– длина пружины в состоянии растяжения,
– её длина в недеформированном состоянии.
Центробежная сила
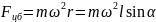 ,
где r
= lsinα.
В состоянии равновесия имеем соотношения:
T
sinα
=
,
где r
= lsinα.
В состоянии равновесия имеем соотношения:
T
sinα
=
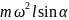 →
T =
→
T =
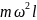 ;Tcosα
= mg.
;Tcosα
= mg.
Итак,
имеется три уравнения: T=k(l-
),
T
=
,
Tcosα
= mg.
Отсюда находим cos
α: k(l-
)
=
→ l
= k
/(k-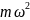 );T=k(
);T=k(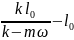 )
=
)
=
 ;
cosα
= mg/T
= mg*
;
cosα
= mg/T
= mg*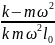 =
=
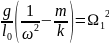 (
(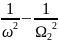 )
=
)
=
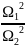 (
( -1).Здесь
0
-1).Здесь
0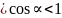 ,
т.е.
,
т.е.
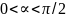 .Отсюда
.Отсюда
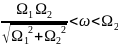
2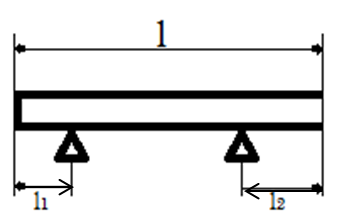 .11.
Балка
массы
.11.
Балка
массы
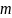 =300
кг и длины
=300
кг и длины
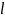 =8,00
м лежит на двух опорах (рис.) Расстояния
от концов балки до опор:
1=2,00
м,
2=1,00
м. Найти силы
1
и
2,
с которыми балка давит на опоры.
=8,00
м лежит на двух опорах (рис.) Расстояния
от концов балки до опор:
1=2,00
м,
2=1,00
м. Найти силы
1
и
2,
с которыми балка давит на опоры.
Решение. Балка при действии на нее сил тяжести и нормальных реакций со стороны опор находится в равновесии (покое).
В
этом состоянии результирующая сила и
результирующий момент сил относительно
любой точки (например, центра масс) равны
нулю. Поэтому можно написать:
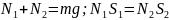 ,
где
,
где
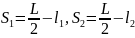 – плечи действия сил
– плечи действия сил
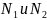 .
Из системы этих уравнений находим:
.
Из системы этих уравнений находим:
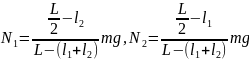 .
.
При
этом силы давления на опоры равны: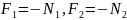 .
Для m=300кг,
l=8м,
.
Для m=300кг,
l=8м,
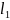 =2м,
=2м,
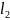 =1м:
|
=1м:
|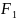 |=1,76*
|=1,76* |
| =1,18*
=1,18*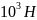 .
.
2.12.
Найти
момент инерции однородной прямоугольной
пластинки массы
,
длины
и ширины
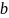 относительно перпендикулярной к ней
оси, проходящей через: а) центр
пластинки, б) одну из вершин пластинки.
относительно перпендикулярной к ней
оси, проходящей через: а) центр
пластинки, б) одну из вершин пластинки.
Р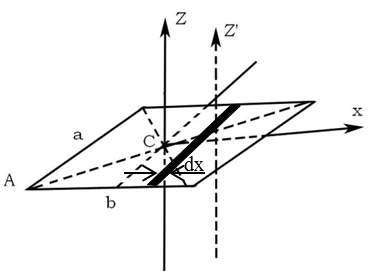 ешение.
Выделим
полоску шириной
параллельно, например, стороне «
»
прямоугольника; масса этой полоски
ешение.
Выделим
полоску шириной
параллельно, например, стороне «
»
прямоугольника; масса этой полоски
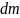 =
=
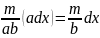 .
Момент инерции этого элемента пластинки
относительно оси
.
Момент инерции этого элемента пластинки
относительно оси
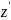 :
d
:
d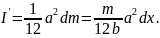 По теореме Штейнера момент инерции того
же элемента относительно оси
По теореме Штейнера момент инерции того
же элемента относительно оси
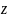 :
d
:
d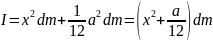 =
=
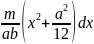 .
Момент инерции пластинки в целом
относительно оси
:
.
Момент инерции пластинки в целом
относительно оси
:
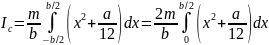 =
=
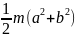 .
.
Момент
инерции относительно оси, проходящей
через вершину пластинки и перпендикулярную
ей, равен:I=
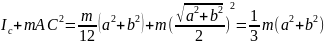 .
.
2.13. Прямой круглый однородный конус имеет массуm и радиус основания R. Найти момент инерции I конуса относительно его оси.
Решение.
Объем
конуса разбиваем на тонкие круглые
диски, перпендикулярные оси симметрии
.
Радиус элементарного диска ,
,
е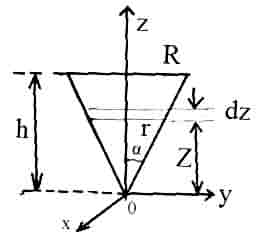 го
масса
го
масса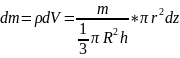
 Момент
инерции:
Момент
инерции: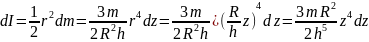 .Момент
инерции конуса
.Момент
инерции конуса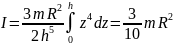
2 .14.
Однородный
цилиндр массы m и радиуса r катится без
скольжения по горизонтальной плоскости.
Центр цилиндра движется со скоростью
.14.
Однородный
цилиндр массы m и радиуса r катится без
скольжения по горизонтальной плоскости.
Центр цилиндра движется со скоростью
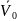 (см.рис.).
Найти модуль момента импульса цилиндра
относительно точек 1, 2 и 3, которые лежат
в перпендикулярной к цилиндру плоскости,
проходящей через его центр.
(см.рис.).
Найти модуль момента импульса цилиндра
относительно точек 1, 2 и 3, которые лежат
в перпендикулярной к цилиндру плоскости,
проходящей через его центр.
Решение.
Момент импульса тела относительно
произвольно заданной неподвижной точки
( например, 1, 2 или 3) определяется суммой
собственного момента импульса
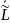 и момента импульса
и момента импульса
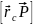 ,
обусловленного поступательным движением
тела как целого, т.е.
,
обусловленного поступательным движением
тела как целого, т.е.
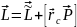 .
В проекциях на ось z,
которую проведем перпендикулярно
плоскости рисунка и от нас, это равенство
представим в виде
.
В проекциях на ось z,
которую проведем перпендикулярно
плоскости рисунка и от нас, это равенство
представим в виде
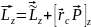 .
.
В
рассматриваемом случае
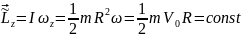 при
при
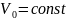 .
Моменты импульса катящегося цилиндра
относительно точек 1, 2, 3 соответственно
равны:
.
Моменты импульса катящегося цилиндра
относительно точек 1, 2, 3 соответственно
равны:
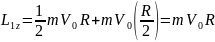
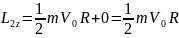
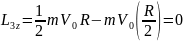
2.15. Однородный шарик помещен на плоскость, образующую угол α=30,0° с горизонтом.
1.
При каких значениях коэффициента трения
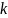 шарик будет скатываться с плоскости
без скольжения?
шарик будет скатываться с плоскости
без скольжения?
2. Полагая =0,100, а) определить характер движения шарика, б) найти значения скоростей точек A, В и С шарика спустя =1,00 с после начала движения.
Р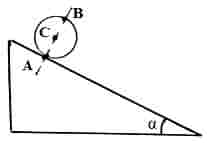 ешение.
Напишем уравнения поступательного
движения шарика вдоль наклонной плоскости
и вращательного движения вокруг оси
ешение.
Напишем уравнения поступательного
движения шарика вдоль наклонной плоскости
и вращательного движения вокруг оси
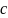 ,
полагая, что скольжения нет:
,
полагая, что скольжения нет:
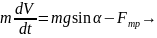
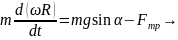
|
|
|
|
Уравнения (1) и (2) совместно дают:
|
|
Подставляя
(3) в (1), получим
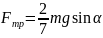 (4).
(4).
Скольжение
отсутствует, если
 .
Максимальная сила трения
.
Максимальная сила трения
 .
Итак, имеем:
.
Итак, имеем:

При
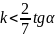 шарик
будет скользить по наклонной плоскости,
вращаясь одновременно.
шарик
будет скользить по наклонной плоскости,
вращаясь одновременно.
2.16. Однородный сплошной цилиндр массы =1,00 кг висит в горизонтальном положении на двух намотанных на него невесомых нитях (рис.). Цилиндр отпускают без толчка.
а)
За сколько времени
цилиндр опустится на расстояние
 =50,0
см?
=50,0
см?
б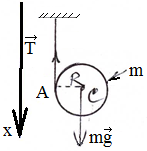 )
Какое натяжение
испытывает при опускании цилиндра
каждая из нитей?
)
Какое натяжение
испытывает при опускании цилиндра
каждая из нитей?
Решение.
На рисунке вектор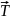 определяет силу натяжения обеих нитей.
В данной системе цилиндр совершает
поступательное движение вертикально
вниз и вращательное движение вокруг
оси
определяет силу натяжения обеих нитей.
В данной системе цилиндр совершает
поступательное движение вертикально
вниз и вращательное движение вокруг
оси
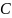 .
Соответствующие уравнения имеют вид:
.
Соответствующие уравнения имеют вид:
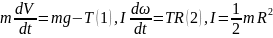 .
.
В
уравнениях (1) и (2) содержится 3 неизвестных
величины: сила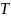 и ускорения
и ускорения
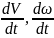 .
Поэтому напишем уравнение вращательного
движения тела относительно оси А:
.
Поэтому напишем уравнение вращательного
движения тела относительно оси А:
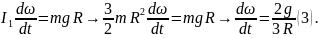 Подставляем (3) в (2):
Подставляем (3) в (2):
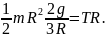 Отсюда
находим
Отсюда
находим
 (4). Из (1) и (4) получаем ускорение опускания
цилиндра:
(4). Из (1) и (4) получаем ускорение опускания
цилиндра:
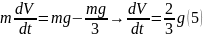 .
Из (5) с учетом начального условия
.
Из (5) с учетом начального условия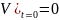 следует:
следует:
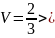 .
При этом за время t
цилиндр опустится навысоту
.
При этом за время t
цилиндр опустится навысоту
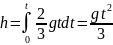 .
Отсюда
.
Отсюда
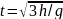 .
Для h=0,5м
t=0,4с.
На основании (1) и (5) находим силу натяжения
одной нити:
.
Для h=0,5м
t=0,4с.
На основании (1) и (5) находим силу натяжения
одной нити:
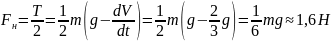 .
.
2.17.
На
ступенчатый блок (см.рис)
намотаны
в противоположных направлениях две
нити. На конец одной нити действуют
постоянной силой
,
а к концу другой нити прикреплен груз
массы m. Известны радиусы ступенчатого
блока ,
,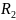 ,
момент инерции блока относительно оси
вращения
,
момент инерции блока относительно оси
вращения
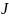 .
Трения нет. Найти угловое ускорение
блока.
.
Трения нет. Найти угловое ускорение
блока.
Р ешение.
Обозначим
силу натяжения правого участка нити
через Т и напишем уравнение движения
тел данной системы:
ешение.
Обозначим
силу натяжения правого участка нити
через Т и напишем уравнение движения
тел данной системы:
1) для груза mMa=mg-T (1),
2)
для блока
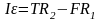 (2).
(2).
Здесь
 – угловое ускорение блока, которое
связано с тангенциальным ускорением
– угловое ускорение блока, которое
связано с тангенциальным ускорением
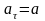 соотношением
соотношением
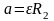 (3).
Исключая из системы равенств (1) и (2)
величину Т с учетом соотношения (3),
получим:
(3).
Исключая из системы равенств (1) и (2)
величину Т с учетом соотношения (3),
получим:
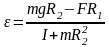 .
.
2.18.
Однородный цилиндр радиуса
раскрутили вокруг его оси до угловой
скорости
 и
поместили затем в угол (см.рис). Коэффициент
трения между стенками угла и цилиндром
равен
.
Сколько времени цилиндр будет вращаться
в этом положении?
и
поместили затем в угол (см.рис). Коэффициент
трения между стенками угла и цилиндром
равен
.
Сколько времени цилиндр будет вращаться
в этом положении?
Решение.Действующие
на данное тело силы показаны на рисунке.
Поскольку данное тело не совершает
поступательного движения, то
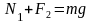 ,
,
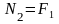 .
Если учесть, что силы трения
.
Если учесть, что силы трения
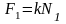 ,
,
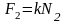 ,
то из предыдущих соотношений следует:
,
то из предыдущих соотношений следует:
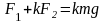 ,
,
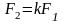 .
Отсюда получаем:
.
Отсюда получаем: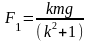 ,
,
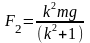 .
.
Т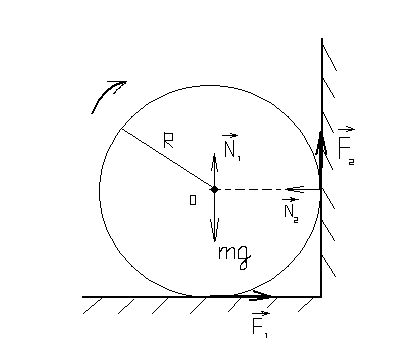 еперь
нам необходимо найти угловую скорость
еперь
нам необходимо найти угловую скорость
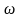 замедленного вращения цилиндра. Из
динамического уравнения
замедленного вращения цилиндра. Из
динамического уравнения
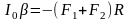 угловое ускорение
угловое ускорение
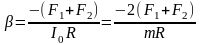 .
Подставляя выражения для
.
Подставляя выражения для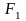 и
и
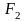 ,
получим
,
получим
 .
Угловая скорость в произвольный момент
времени
.
Угловая скорость в произвольный момент
времени
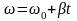 .
В момент остановки
.
В момент остановки
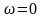 .
Следовательно, время вращения цилиндра
до остановки будет равно
.
Следовательно, время вращения цилиндра
до остановки будет равно
 .
.
2.19. Маховик с начальной угловой скоростью начинает тормозиться силами, момент которых относительно его оси пропорционален квадратному корню из его угловой скорости. Найти среднюю угловую скорость маховика за все время торможения.
Решение.
Согласно
условию момент тормозящих сил, действующих
на раскрученный маховик,
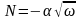 ,
где
,
где
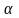 >0
– некоторая постоянная,
- модуль мгновенной угловой скорости
вращения. Из уравнения
>0
– некоторая постоянная,
- модуль мгновенной угловой скорости
вращения. Из уравнения
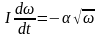 вращательного движения маховика
относительно неподвижной оси легко
установить зависимость
вращательного движения маховика
относительно неподвижной оси легко
установить зависимость
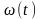 :
: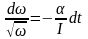 ,
,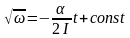 .
Для t
= 0
.
Для t
= 0
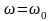 ,
следовательно,
,
следовательно,
![]() и
и
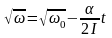 ,
т. е.
,
т. е.
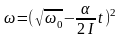 .
Длительность
.
Длительность
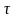 вращения маховика найдём из условия
:
вращения маховика найдём из условия
:
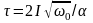 .
При этом средняя скорость вращения
маховика равна
.
При этом средняя скорость вращения
маховика равна
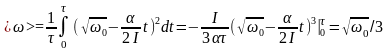 .
.
2.20.
Двухступенчатый
блок радиусов
и
положили
на гладкую горизонтальную поверхность.
На ступени блока плотно намотаны нити,
к концам которых приложили постоянные,
взаимно перпендикулярные силы
и
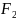 (рис., вид сверху). Сколько оборотов
совершит блок за время, в течение которого
его ось С переместится на расстояние
?
Масса данного блока
,
его момент инерции относительно оси С
равен
(рис., вид сверху). Сколько оборотов
совершит блок за время, в течение которого
его ось С переместится на расстояние
?
Масса данного блока
,
его момент инерции относительно оси С
равен
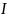 .
.
Решение.
Результирующее
движение ступенчатого блока рассматриваем
как наложение поступательного движения
и его вращения вокруг собственной оси
С. Уравнения этих движений имеют вид,
полагая, что
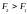 :
:
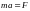 ,
где
,
где
 .
Время перемещения блока на расстояние
.
Время перемещения блока на расстояние
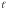 найдем из соотношения
найдем из соотношения
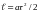 ,
F=const,
,
F=const,
 =const,начальные
=const,начальные
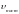 и
и
 равны нулю:
равны нулю:
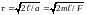 .
Угловое ускорение
.
Угловое ускорение
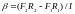 .
Угловой путь блока за время
.
Угловой путь блока за время
 равен
равен
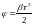 ,
а совершенное число оборотов
,
а совершенное число оборотов
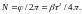
Подставляя
сюда выражения для и
,
получим:
и
,
получим:
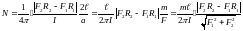 .
.
2.21. Сплошному однородному цилиндру массы и радиуса сообщили вращение вокруг его оси с угловой скоростью , затем его положили боковой поверхностью на горизонтальную плоскость и предоставили самому себе. Коэффициент трения равен . Найти: а) время, в течение которого движение цилиндра будет происходить со скольжением; б) полную работу силы трения скольжения.
Р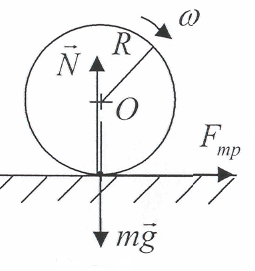 ешение.
На
первой стадии угловая скорость вращения
цилиндра ω>v/R,
где
v-
скорость
качения. Под действием тормозящего
момента сил трения через некоторый
промежуток времени τ угловая скоростьω(τ)
= v(τ)/R.
(1)
ешение.
На
первой стадии угловая скорость вращения
цилиндра ω>v/R,
где
v-
скорость
качения. Под действием тормозящего
момента сил трения через некоторый
промежуток времени τ угловая скоростьω(τ)
= v(τ)/R.
(1)
Отсюда
видно, что для определения времени τ
необходимо предварительно установить
зависимости ω(t)
и
v(t)
на
стадии скольжения цилиндра. Из уравнений
поступательного и вращательного движений
цилиндра та=Fтр
= kmgи
 mR2
β= -RFmp=-kmgRнаходим
ускоренияа=kgи
β=-2kg/R.
'Гак
как а
и
β
константы, то v=at=kgt(v0=0)
mR2
β= -RFmp=-kmgRнаходим
ускоренияа=kgи
β=-2kg/R.
'Гак
как а
и
β
константы, то v=at=kgt(v0=0)
и ω=ω0+βt=ω0 - 2kgt/R. Удовлетворяя условию (1), получим τ=ω0R/3kg. При этом ω(τ)=ω0/3.
Работа сил трения скольжения равна прирщению кинетической энергии данного тела:
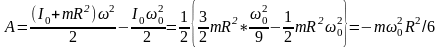
2.22.
На
гладкой горизонтальной поверхности
лежит однородный стержень массы
и длины
.
На один из его концов начали действовать
постоянной, направленной все время
вертикально вверх силой
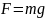 .
Найти угловую скорость стержня в
зависимости от угла
его поворота.
.
Найти угловую скорость стержня в
зависимости от угла
его поворота.
Решение.
В
отношении положительной к стержню силы
 =-m
=-m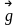 необходимо
принять одно из дополнительных условий:
вектор силы может перемещаться в
горизонтальном направлении, оставаясь
параллельным самому себе или точка
приложения этого вектора остается на
одной и той же вертикали. Рассмотрим
сначала первый вариант.
необходимо
принять одно из дополнительных условий:
вектор силы может перемещаться в
горизонтальном направлении, оставаясь
параллельным самому себе или точка
приложения этого вектора остается на
одной и той же вертикали. Рассмотрим
сначала первый вариант.
В
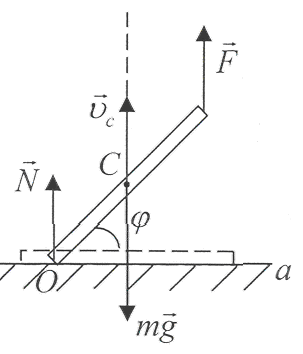 этом случае центр масс стержня под
действием приложенной силы получает
только вертикальное перемещение (см.
рисунок). Пусть в процессе движения
угол поворота стержня равен φ.
При
этом значении угла поворота центр масс
стержня поднимется на высоту hc=(l/2)sinφ,
aero
скорость будет равна vc=dhc/
dt=(ωl/2)cosφ,
где
ω - угловая скорость поворота стержня
в рассматриваемый момент времени. К
этому моменту стержень приобретает
кинетическую энергию
этом случае центр масс стержня под
действием приложенной силы получает
только вертикальное перемещение (см.
рисунок). Пусть в процессе движения
угол поворота стержня равен φ.
При
этом значении угла поворота центр масс
стержня поднимется на высоту hc=(l/2)sinφ,
aero
скорость будет равна vc=dhc/
dt=(ωl/2)cosφ,
где
ω - угловая скорость поворота стержня
в рассматриваемый момент времени. К
этому моменту стержень приобретает
кинетическую энергию
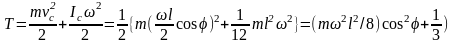 При
этом, совершенная силой
=-m
работа,
равна А=Flsinφ=mglsinφ.
Эта
работа пойдет на приращение кинетической
энергии
При
этом, совершенная силой
=-m
работа,
равна А=Flsinφ=mglsinφ.
Эта
работа пойдет на приращение кинетической
энергии
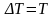 и
потенциальной энергии стержня
и
потенциальной энергии стержня
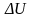 =mghc=(mgl/2)sinφ.
Итак,
имеем равенство
mglsinφ=(mω2l2/8)(cos2φ+1/3)+(mgl/2)sinφ.
Отсюда
следует, что gsinφ(ω2/4)(cos2φ+1/3)
и φ
=mghc=(mgl/2)sinφ.
Итак,
имеем равенство
mglsinφ=(mω2l2/8)(cos2φ+1/3)+(mgl/2)sinφ.
Отсюда
следует, что gsinφ(ω2/4)(cos2φ+1/3)
и φ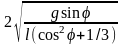
2) Теперь рассмотрим случай, когда центр масс стержня одновременно перемещается вверх и в сторону вертикали, вдоль которой действует приложенная сила .
Обращаясь к рисунку, запишем координаты центра масс стержня: Хс=(l-lcosφ)+(l/2)cosφ=(l/2)(2-cosφ),yt=(l/2)sinφ. (1)
Д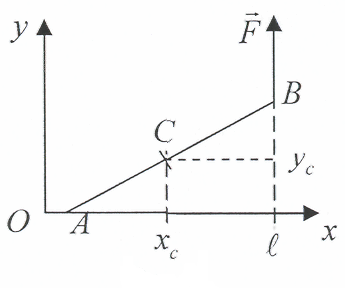 ифференцируя
равенства (1) по времени, получим компоненты
и модуль скорости центра масс стержня:
vсх=(ωl.2)sinφ,
vсу=(ωl/2)cosφ,
vc=
ωl/2.
ифференцируя
равенства (1) по времени, получим компоненты
и модуль скорости центра масс стержня:
vсх=(ωl.2)sinφ,
vсу=(ωl/2)cosφ,
vc=
ωl/2.
Кинетическая
энергия стержня для φповорота
равна Т=т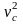 /2+Icω2/2=тω2l2/6.
Из энергетического соотношения
А=Flsinφ=Т+mglsinφ/2
найдем угловую скорость стержня
/2+Icω2/2=тω2l2/6.
Из энергетического соотношения
А=Flsinφ=Т+mglsinφ/2
найдем угловую скорость стержня
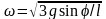 .
.
2.23.
Волчок
массы
= 0,50 кг, ось которого наклонена под углом
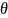 = 30° к вертикали, прецессирует под
действием силы тяжести. Момент инерции
волчка относительно его оси симметрии
= 2,0 г*м2,
угловая скорость вращения вокруг этой
оси
= 350 1/с, расстояние от точки опоры до
центра масс волчка
= 10 см. Найти: а) угловую скорость прецессии
волчка; б) модуль и направление
горизонтальной составляющей силы
реакции, действующей на волчок в точке
опоры.
= 30° к вертикали, прецессирует под
действием силы тяжести. Момент инерции
волчка относительно его оси симметрии
= 2,0 г*м2,
угловая скорость вращения вокруг этой
оси
= 350 1/с, расстояние от точки опоры до
центра масс волчка
= 10 см. Найти: а) угловую скорость прецессии
волчка; б) модуль и направление
горизонтальной составляющей силы
реакции, действующей на волчок в точке
опоры.
Р ешение.
Угловая
скорость прецессии волчка вокруг
вертикальной оси. проходящей через
неподвижную точку О(см. рис.), равна
ешение.
Угловая
скорость прецессии волчка вокруг
вертикальной оси. проходящей через
неподвижную точку О(см. рис.), равна
 ,
где l=ОС,
точка С - центр масс волчка. Во вращающейся
системе координат с угловой скоростью
ωгоризонтальная составляющая силы
реакции в точке О равна центробежной
силе инерции, обусловленной прецессионным
вращением волчка, т.е. R=тω'2lsinθ.
При
числовых значениях данных величин
ω’=0,7
,
где l=ОС,
точка С - центр масс волчка. Во вращающейся
системе координат с угловой скоростью
ωгоризонтальная составляющая силы
реакции в точке О равна центробежной
силе инерции, обусловленной прецессионным
вращением волчка, т.е. R=тω'2lsinθ.
При
числовых значениях данных величин
ω’=0,7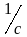 ,
R=10
мН.
,
R=10
мН.
2.24. Волчок, масса которого = 1,0 кг и момент инерции относительно собственной оси = 4,0г*м2, вращается с = 320 рад/с. Его точка опоры находится на подставке, которую перемещают в горизонтальном направлении с ускорением = 3,0 м/с2. Расстояние между точкой опоры и центром масс волчка = 10 см. Найти модуль и направление вектора ' — угловой скорости прецессии волчка.
Р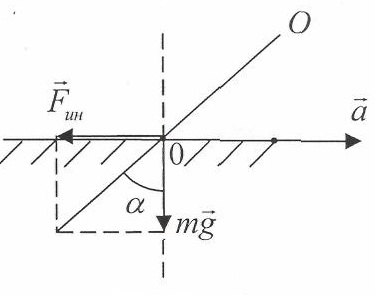 ешение.
Относительно
ускоряющейся платформы создается
однородное результирующее поле сил
тяжести и инерции, которому можно
сопоставить ускорение, модуль которого
равен
ешение.
Относительно
ускоряющейся платформы создается
однородное результирующее поле сил
тяжести и инерции, которому можно
сопоставить ускорение, модуль которого
равен
 .
Ускорение
.
Ускорение
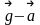 образует с земной вертикалью угол
а=arctg
образует с земной вертикалью угол
а=arctg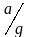 (см.
рисунок). Ось 00, проходящая через
неподвижную точку О гироскопа и
параллельная вектору
(см.
рисунок). Ось 00, проходящая через
неподвижную точку О гироскопа и
параллельная вектору
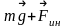 ,
будет являться ось прецессии. При этом
угловая скорость прецессии гироскопа
будет равна
,
будет являться ось прецессии. При этом
угловая скорость прецессии гироскопа
будет равна
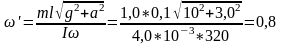 1/c;
1/c;
Угол,
образуемый вектором
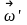 с вертикалью, равен a=arctg
=arctg
с вертикалью, равен a=arctg
=arctg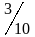 =17°.
=17°.