Контрольные вопросы и задания

1. Дать определение нелинейной регресиии.

2. Как на практике проводят нелинейный множественный регрессионный анализ?

3. Запишите доверительный интервал для коэффициентов регрессии.

Пример решения задачи

Рассмотрим модель 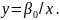В этом случае

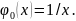
Оценки коэффициентов модели ищем по формулам:

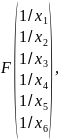
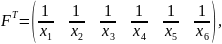
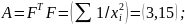
Вычисляем обратную матрицу:

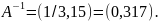
По формуле находим оценку коэффициента:

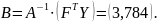
Таким образом уравнение регрессии принимает вид

.

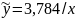Для сравнения моделей вычисляем остаточную дисперсию по формуле: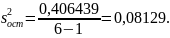

Переходим в уравнении регрессии к исходным переменным:

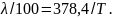
Откуда окончательно получаем

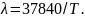
Задачи и упражнения для самостоятельной работ

Решить задачи: [2]. 536, 538.

Форма контроля: устный опрос.

Тема 3 Статистическая проверка статистических гипотез

[1] с. 281-346 .Контрольные вопросы и задания

1. Рассказать о критериях Бартлети, Кочрена, Кендалла, Пирсона.

2. В чем заключается метод графической проверки гипотезы о нормальном распределении генеральной совокупности? Что вы знаете о методе спрямленных диаграмм?

Пример. Используя критерий Пирсона, при уровне значимости 0,05 проверить, согласуется ли гипотеза о распределении генеральной совокупности Х по закону Пуассону с эмпирическим распределением выборки объема n =2 00.

xi	0	1	2	3	4
ni	116	56	22	4	2

Решение.

Выборочная средняя x_в=( x_i n_i )/n=0.6. Предполагаемый закон Пуассона имеет вид: P_n(i)=(0.6)ⁱ exp(-0.6)/i!, т. е. P₀=P₂₀₀(0)=0.5488, P₁=P₂₀₀(1)=0.3293, P₂=P₂₀₀(2)=0.0988, P₃=P(3)=0.0198, P₄=P₂₀₀(4)=0.0030. Теоретические частоты m_i=nP_i=200P_i. Определим m₀=109.76, m₁=65.86, m₂=19.76, m₃=3.96, m₄=0.6. Малочисленные частоты m₃, m₄ можно объединить в новые n₃=4+2=6 и m₃=3.96+0.6=4.56.

Теоретическая частота ² = (n_i-m_i)² /m_i=2.54. По таблице критических точек распределения (см. приложение 5 [4]), по уровню значимости  =0.05 и числу степеней свободы k=s-2=2 находим критическую точку правосторонней критической области _кр² (0.05,2)=6.0. Так как ² < _кр², то имеется подтверждение гипотезы о распределение случайной величины X по закону Пуассону.

Форма контроля: устный опрос, типовой расчет.

Тема 4 Решение неоднородных уравнений с частными производными гиперболического типа методом Фурье

[3] с. 119-126, 136-137.

Пример. Решить неоднородное уравнение гиперболического типа

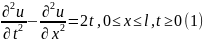
при однородных краевых условиях

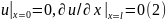
и нулевых начальных условиях

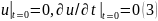
Задача описывает вынужденные колебания однородной

струны, закрепленной на концах, под действием внешней

возмущающей силы 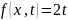. Применяя метод Фурье

разделения переменных, полагаем 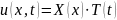для

решения соответствующего однородного уравнения

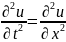
при начальных условиях. Подставив 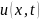это уравнение,

получаем равенство

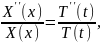
Возможное лишь в случае, если обе части его не зависят ни от x, ни от t, т.е. представляет собой одну и ту же постоянную. Обозначим эту постоянную через с: 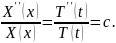Используем краевые условия: 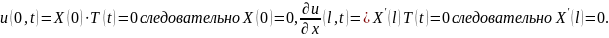Таким образом, приходим к задаче Штурма-Лиувилля: найти такие значения параметра с, при которых существуют нетривиальные (т.е. отмеченные от тождественного нуля) решения уравнения, удовлетворяющие краевым условиям

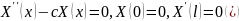
При 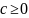в общем решение уравнения, согласно краевым

условиям, с₁=0, с₂=0 и решение задачи (*) становятся

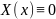– случаи не интересны. При с>0, с=-λ²: общее решение вида: X(x)=c₁ cosλx + c₂ sinλx, X(x)=-c₁ λsinλx+c₂λcosλx.

X(0)=c₁1+c₂0=c₁=0, X’(l)=c₂λcosλl=0, 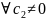считаем.

Поэтому cosλl=0. Находим ее собственные значения

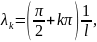и соответствующие им собственные функции X_k(x)=inλ_kx, k=0,1,2,…,определяемые с точностью до постоянного множителя, который мы полагаем равным единице.

Следовательно, лишь при с=-λ²_к, к=0,1,2,…, имеем

нетривиальные решения задачи (*). Теперь решение задачи ищем в виде Фурье

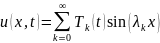, где ,

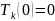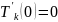
Подставляя в основное уравнение , получаем

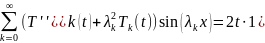
Для нахождения функций 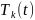разложим функцию 1 в ряд

Фурье по синусам на интервале (0,1):

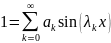, Так как

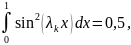то получаем уравнение

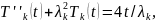
Общее решение которого, имеет вид

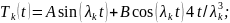
Значения неопределенных коэффициентов: А=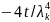 , В=0. И

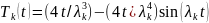
Окончательно:

.

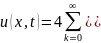Форма контроля: устный опрос.