Метод наименьших квадратов как частный случай метода максимального правдоподобия.

Пусть случайная величина Х имеет нормальное распределение с параметрами , т.е. функция

плотности ,

причем числовое значение параметра неизвестно, а значение параметра известно. Для нахождения оценки параметра воспользуемся методом максимального правдоподобия.

Функция правдоподобия

Найдем (**)

Найдем max функции , рассматривая ее как функцию параметра «а». Однако не будем использовать первую и вторую производные функции , а поступим следующим образом. Из равенства (**) видно, что функция , рассматриваемая как функция от «а», достигает максимального значения в том и только в том случае, когда сумма достигает минимального значения, таким образом, в случае нормального распределения оценку 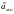максимального правдоподобия можно определить как точку минимума функции:

,

т.е. из условия

(***)

Метод нахождения оценки параметра «а» в соответствии с последним требованием (***) называется методом наименьших квадратов.

Найдем точку минимума функции F(a)

Найдем критическую точку из условия

.

Т.к. вторая производная

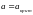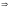
при любом значении «а», в том числе и при , то 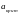– точка min функции и ее нужно принять в качестве оценки максимального правдоподобия параметра «а». Итак

Следует знать.

1). Оценки, получаемые методом наименьших квадратов и методом максимального правдоподобия, не всегда совпадают.

2) При оценивании параметра нормального распределения предполагалось, что значение дисперсии неизвестно. Если не известны ни , ни , то функцию

следует рассматривать как функцию от и и для нахождения оценок и максимального правдоподобия следует решить систему уравнений правдоподобия:

Основные принципы статистического контроля качества в ходе производства

Рассмотрим контроль некоторого количественного параметра, например, размер обрабатываемой детали.

Пусть процесс производства приведены в устойчивое состояние.

Будем считать сначала, что распределение размеров детали точно или приближенно следует нормальному закону с центром и дисперсией . За и можно принять среднюю и дисперсию размеров достаточно большой партии деталей .

Если следить непрерывно за производственным процессом, можно отметить, что большинство размеров будет очень мало отличаться от средней .

Если распределение размеров точно подчиняется нормальному закону, то можно ожидать, что в достаточно большой партии деталей, приблизительно в 95 % деталей , размеры будут отличаться от средней не больше, чем на , приблизительно в 99,7% деталей размеры будут отличаться от средней а не больше, чем .

Это значит, что деталей, размеры которых отличаются от средней более, чем на утроенную сигму ( ) можно ожидать примерно три тысячу. Поэтому, если в небольшой партии деталей обнаружена деталь с размером, отличающимся от средней более, чем на утроенную сигму, то это сигнализирует о нарушении нормальности распределения или о появлении систематической ошибки, т.е. о нарушении устойчивости производственного процесса.

На этом принципе, главным образом, и основан систематический контроль качества продукции в ходе ее производства. Однако практическое осуществление контроля в указанной форме было бы мало эффективным. Это объясняется тем, что практически распределение размеров деталей более или менее отличается от нормального.

Эффективность указанного метода можно увеличить, рассматривая не размеры каждой детали в отдельности, а средние размеры деталей в последовательных равновеликих партиях.

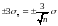Действительно, мы знаем, что средние размеры партии из деталей будут достаточно точно следовать нормальному закону распределения с тем же центром и с дисперсией . Поэтому, если через определенные промежутки времени выбирать партию из обработанных деталей, то средний размер в партии может случайно отклоняться от не более, чем , то это свидетельствует о наличии систематических ошибок, т.е. о нарушении устойчивости производственного процесса.