
- •Справочник магнитного диска (Кафедра высшей математики и физико-математического моделирования)
- •Введение
- •1. Случайные события
- •1.1. Пространство элементарных исходов
- •1.2. События, действия над ними
- •1.3. Сигма-алгебра событий
- •1.4. Решение типовых примеров
- •2. Вероятность
- •2.1. Классическое определение вероятности
- •2.2. Вычисление вероятностей с помощью формул комбинаторики
- •2.3. Геометрическое определение вероятности
- •2.4. Статистическое определение вероятности
- •2.5. Аксиоматическое определение вероятности
- •2.6. Решение типовых примеров
- •Вопросы и задачи
- •3. Условная вероятность. Схема Бернулли
- •3.1. Определение условной вероятности
- •3.2. Формула умножения вероятностей
- •3.3. Независимые и зависимые события
- •3.4. Формула полной вероятности
- •3.5. Формула Байеса
- •3.6. Схема Бернулли
- •3.7. Решение типовых примеров
- •4. Одномерные случайные величины
- •4.1. Определение случайной величины
- •4.2. Функция распределения случайной величины
- •4.3. Дискретные случайные величины
- •4.4. Некоторые дискретные случайные величины
- •4.5. Непрерывные случайные величины
- •4.6. Некоторые непрерывные случайные величины
- •4.7. Решение типовых примеров
- •5. Многомерные случайные величины
- •5.1. Многомерная случайная величина. Совместная функция распределения
- •5.2. Дискретные двумерные случайные величины
- •5.3. Непрерывные случайные величины
- •5.4. Независимые случайные величины
- •6. Числовые характеристики случайных величин
- •6.1. Математическое ожидание случайной величины
- •6.2. Математическое ожидание. Свойства математического ожидания
- •6.3. Дисперсия. Моменты высших порядков
- •6.4. Ковариация и коэффициент корреляции случайных величин
- •6.5. Решение типовых примеров
- •7. Условные характеристики случайных величин
- •Условные распределения
- •7.2. Условные числовые характеристики
- •8. Предельные теоремы теории вероятностей
- •Сходимость последовательности случайных величин
- •8.2. Неравенства Чебышева. Закон больших чисел
- •9. Элементы математической статистики
- •9.1. Выборочный метод. Основные понятия
- •9.2. Статистическое распределение. Полигон и гистограмма
- •9.3. Эмпирическая функция распределения
- •9.4 Оценка параметров по выборке. Понятие несмещенности , состоятельности и эффективности оценки
- •9.5. Генеральная средняя. Выборочная средняя.
- •9.6. Генеральная дисперсия. Выборочная дисперсия. Эмпирическая дисперсия
- •9.7. Доверительная вероятность. Доверительный интервал
- •10. Математическая обработка результатов наблюдений
- •10. 1. Измерения и их погрешности. Применение методов математической статистики к обработке результатов наблюдений
- •10. 2. Оценка точного значения измеряемой величины
- •Доверительная оценка при неизвестной точности измерений.
- •10.3. Оценки точности измерений
- •Доверительные оценки средней квадратической погрешности.
- •10.4. Метод наименьших квадратов
- •Стационарные случайные процессы
- •Марковские случайные процессы
- •Процесс Пуассона
- •Случайные процессы с независимыми приращениями
- •12. Понятие о нелинейной регрессии Основные понятия
- •Доверительный интервал для коэффициентов
- •Библиографический список
- •ОгЛавление
- •6.1. Математическое ожидание случайной величины 159
- •10.3. Оценки точности измерений 215
- •3 94026 Воронеж, Московский просп.,14
8.2. Неравенства Чебышева. Закон больших чисел
Прежде чем приступить к рассмотрению закона больших чисел, рассмотрим два неравенства Чебышева. Заметим, что неравенства Чебышева представляют и самостоятельный интерес, поскольку в современной теории вероятностей широко используются неравенства такого типа.
Теорема 8.1. Для каждой неотрицательной случайной величины X, имеющей математическое ожидание M(X), при любом > 0 справедливо соотношение
![]() ,
называемое
первым
неравенством Чебышева.
,
называемое
первым
неравенством Чебышева.
Пример
8.1.
Пусть
X
—
время опоздания студента на лекцию,
причем известно, что M(X)
=
1 мин. Воспользовавшись первым неравенством
Чебышева, оценим вероятность
![]() того, что студент опоздает не менее, чем
на 5 мин. Имеем
того, что студент опоздает не менее, чем
на 5 мин. Имеем
![]() .
.
Таким образом, искомая вероятность не более 0,2, т.е. в среднем из каждых пяти студентов опаздывает, по крайней мере, на 5 мин не более чем один студент.
Теорема
8.2. Для
каждой случайной величины Х,
имеющей дисперсию
![]() ,
при любом
> 0
справедливо второе
неравенство Чебышева
,
при любом
> 0
справедливо второе
неравенство Чебышева
![]() .
.
Пример
8.2. Пусть
в условиях предыдущего примера известно
дополнительно, что
![]() .
Оценим минимальное значение
.
Оценим минимальное значение
![]() ,
при котором вероятность опоздания
студента на время не менее
не превышает заданного значения
,
при котором вероятность опоздания
студента на время не менее
не превышает заданного значения
![]() =
0,1.
=
0,1.
Для решения поставленной задачи воспользуемся вторым неравенством Чебышева. Тогда
![]() .
.
Значит,
![]() .
.
Подставляя конкретные значения, имеем
![]() .
.
Таким образом, вероятность опоздания студента на время более 4,16 мин не более 0,1.Сравнивая полученный результат с результатом примера 8.1, видим, что дополнительная информация о дисперсии времени опоздания позволяет дать более точную оценку искомой вероятности.
Определение 8.5. Последовательность случайных величин удовлетворяет закону больших чисел (слабому), если для любого > 0
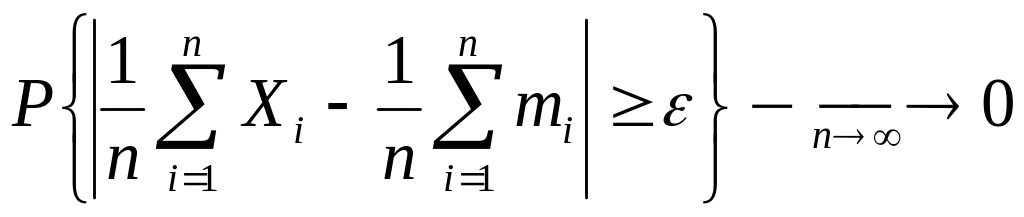 .
.
Иными
словами, выполнение закона больших
чисел отражает предельную устойчивость
средних арифметических случайных
величин: при большом числе испытаний
они практически перестают быть случайными
и совпадают со своими средними значениями.
Очевидно, что последовательность
удовлетворяет закону больших чисел
тогда и только тогда, когда среднее
арифметическое случайных величин
![]() сходится
по вероятности к нулю при
сходится
по вероятности к нулю при
![]() .
.
Теорема
8.3.
Если последовательность
независимых
случайных величин такова,
что существуют
![]() и
и
![]() ,
причем дисперсии
,
причем дисперсии
![]() ограничены
в совокупности (т.е.
ограничены
в совокупности (т.е.
![]() ),
то для последовательности
выполнен закон больших чисел. При этом
говорят также, что к последовательности
случайных величин применим закон
больших чисел в форме Чебышева.
),
то для последовательности
выполнен закон больших чисел. При этом
говорят также, что к последовательности
случайных величин применим закон
больших чисел в форме Чебышева.
Следствие
8.1. Если
случайные величины
,
i=
1,2,..., в условиях теоремы 8.3 являются
также одинаково распределенными (в этом
случае
![]() и
и
![]() ),
то последовательность
случайных величин удовлетворяет закону
больших чисел в следующей форме:
),
то последовательность
случайных величин удовлетворяет закону
больших чисел в следующей форме:
![]() .
.
Теорема 8.4. Пусть проводится п испытаний по схеме Бернулли и Yn — общее число успехов в п испытаниях. Тогда наблюденная частота успехов
![]()
сходится по вероятности к вероятности р успеха в одном испытании, т.е. для любого > 0
![]() .
.
Обозначим число успехов в i-м испытании Бернулли. Тогда частоту успехов в п испытаниях можно определить в виде
![]() ,
причем M
=р и
D
,
причем M
=р и
D![]() = pq.
= pq.
Значит, выполняются все условия следствия 8.1, из которого вытекает утверждение теоремы. Теорему 8.4 называют также теоремой Бернулли, или законом больших чисел в форме Бернулли. Из хода доказательства теоремы 9.4 видно, что закон больших чисел в форме Бернулли является частным случаем закона больших чисел в форме Чебышев.
