5.4. Независимые случайные величины

Определение 5.5. Случайные величины X и Y называют независимыми, если совместная функция распределения является произведением одномерных функций распределения и : .

В противном случае случайные величины называют зависимыми.

Теорема 5.3. Для того чтобы непрерывные случайные величины X и Y были независимыми, необходимо и достаточно, чтобы для всех х и у .

Теорема 5.4. Дискретные случайные величины X и Y являются независимыми тогда и только тогда, когда для всех возможных значений и

.

Мы предоставляем возможность читателю доказать эту теорему самостоятельно.

Определение 5.6. Случайные величины , заданные на одном и том же вероятностном пространстве, называют независимыми в совокупности, если

.

Замечание 5.3. Теоремы 5.3 и 5.4 распространяются на любое число случайных величин.

Пример 5.13. Двумерная случайная величина (X, Y) имеет совместную функцию распределения

Найдем:

а) вероятности событий

;

б) частные функции распределения случайных величин X и Y.

а) В соответствии со свойством 5 двумерной функции распределения имеем

.

Событие представляет собой попадание двумерной случайной величины (X, Y) в квадрант . Поэтому

б) В соответствии со свойством 7 двумерной функции распределения частные распределения случайных величин X и Y задаются формулами

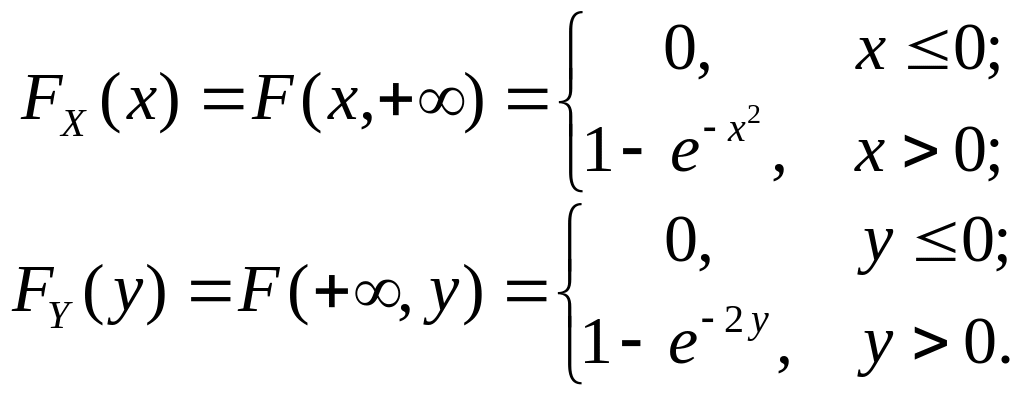
Пример 5.14. Двумерная случайная величина (Х, Y) имеет совместную функцию распределения

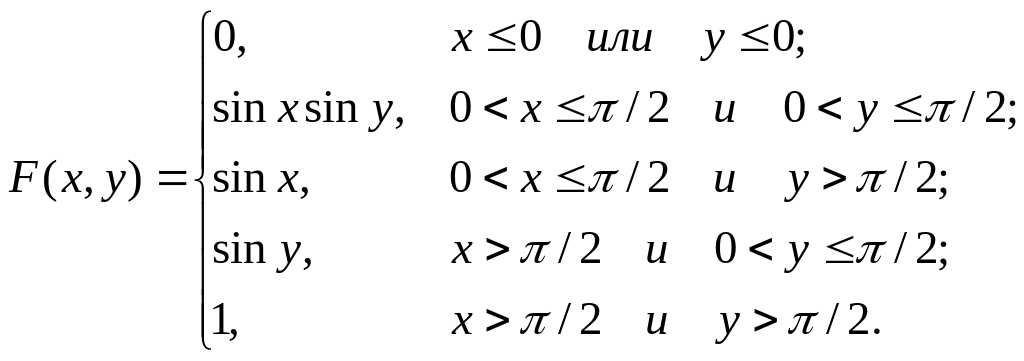
Найдем: а) вероятности событий D₁, D₂, D₃, которые заданы соответственно:

б) частные функции распределения случайных величин X и Y.

Действуя таким же образом, как в примере 5.13, имеем:

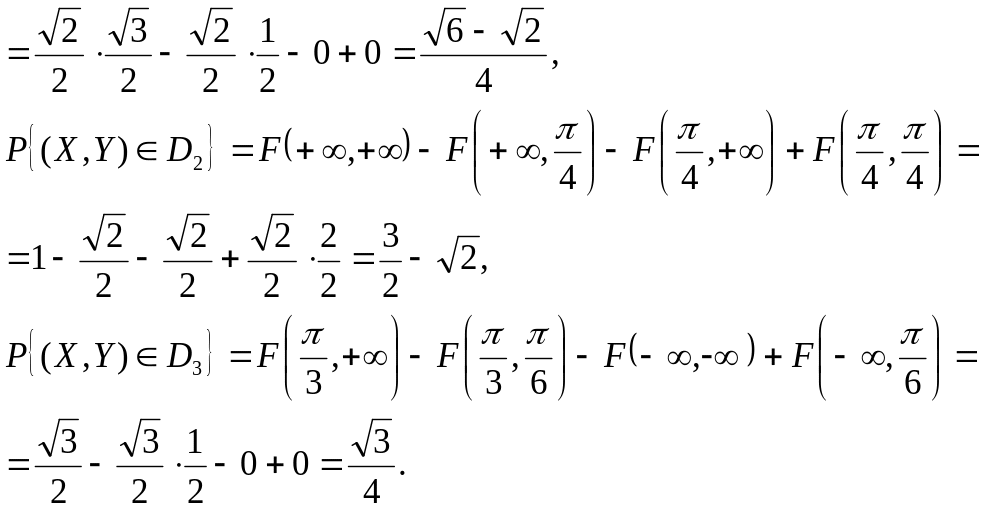
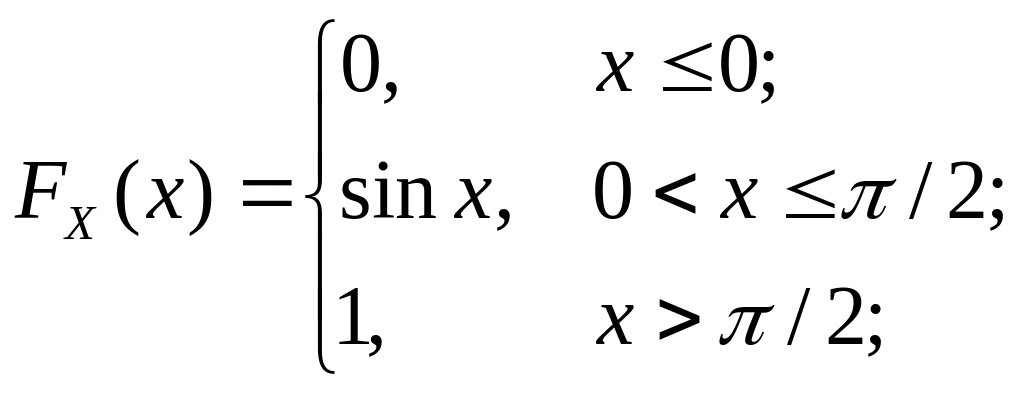
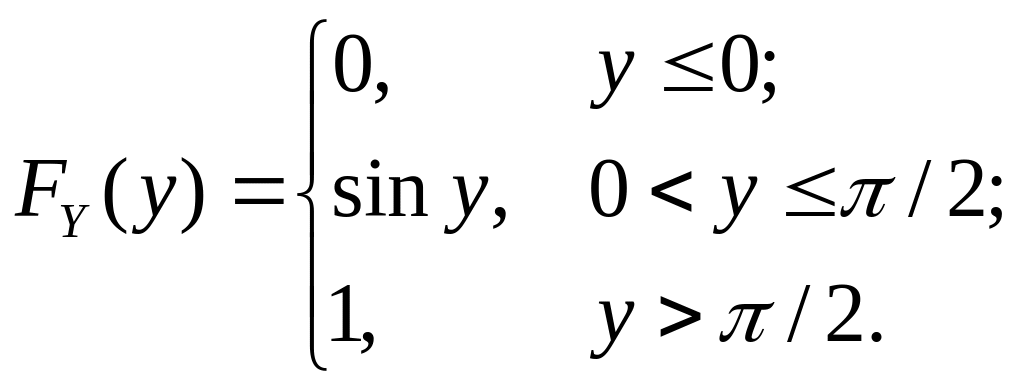
Пример 5.15. Распределение вероятностей дискретной двумерной случайной величины (X, Y) задано табл. 5.2. Найдем: а) ряды распределения случайных величин X и Y;

Таблица 5.2

X	Y
	3	8	12
3	0,17	0,13	0,25
5	0,10	0,30	0,05

б) значения совместной функции распределения F(x,y) в точках (4,5; 8) и (9; 11), а также вероятность события {4 X < 9, 8 Y < 11}.

а) Поскольку событие {X = 3} совпадает с объединением непересекающихся событий

{X = 3, Y = 3}, {X = 3, Y = 8} и {X = 3, Y = 12}, то

Р{Х=3} = Р{Х=3, Y =3} + Р{Х=3, Y =8} + Р{Х=3, Y =12} = 0,55.

Аналогично

Р{Х=5} = Р{Х=5, Y =3} + Р{Х=5, Y =8} + Р{X=3, Y =12} = 0,45.

Ряд распределения случайной величины X приведен в таб. 5.3.

Таблица 5.3 Таблица 5.4

YY	33	88	112
PР	00,27	00,43	00,30

XX	33	55
PP	00,55	00,45

Суммируя вероятности по столбцам (см. табл. 5.2), находим:

Р{Y = 3} = Р{Х = 3, Y = 3} + Р{Х = 5, Y = 3} = 0,27,

Р{Y = 8} = Р{Х = 3, Y = 8} + Р{Х = 5, Y = 8} = 0,43,

Р{Y = 12} = Р{Х = 3, Y = 12} + Р{Х = 5, Y = 12} = 0,30.

Ряд распределения случайной величины Y приведен в табл. 5.4.

б) Используя определение 5.3 совместной функции распределения и то, что событие

{X < 4,5, Y < 8} совпадает с событием {X = 3, Y = 3}, получаем

F(4,5, 8) = Р{Х < 4,5, Y < 8} = Р{Х = 3, Y = 3} = 0,17.

Аналогично событие {X < 9, Y < 11} совпадает с объединением непересекающихся событий

{X = 3, Y = 3}, {X = 3, Y = 8}, {X = 5, Y = 3} и {X = 5, Y = 8}, и, значит,

F(9,ll)=P{X<9, Y <ll}=P{X=3, Y =3}+P{X=3, Y =8}+

Р{Х = 5, Y =3}+Р{Х = 5, Y = 8} = 0,70.

Наконец,

Р{4 X < 9,8 Y < 11} = Р{Х = 5, Y = 8} = 0,30.

Пример 5.16. Совместная функция распределения непрерывной двумерной случайной величины (X, Y) имеет вид

.

Найдем совместную плотность распределения.

Воспользовавшись равенством

,

Получим