6.4. Ковариация и коэффициент корреляции случайных величин
Пусть
(
,
)
—
двумерный
случайный вектор.
Определение 6.6. Ковариацией (корреляционным моментом) cov( , ) случайных величин и называют математическое ожидание произведения случайных величин
и
:
.
Запишем формулы, определяющие ковариацию.
Для дискретных случайных величин и
,
для непрерывных случайных величин и
.
Заметим, что введение понятия ковариации позволяет записать выражение для дисперсии суммы случайных величин и к уже имеющимся свойствам дисперсии добавить еще одно:
(свойство 5 дисперсии), справедливое для произвольных, а не только независимых случайных величин X и Y. Действительно,
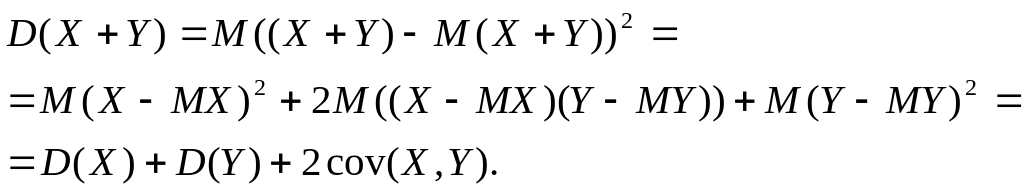
Свойство 5 дисперсии допускает обобщение на произвольное число слагаемых:
/
Следующая теорема устанавливает основные свойства ковариации.
Теорема 6.3. Ковариация имеет следующие свойства
1. cov(X,X) = D(X).
2. cov( , ) = 0 для независимых случайных величин и .
3.
Если
,
то
.
4.
.
5.|
(6.8)
тогда и только тогда, когда случайные величины и связаны линейной зависимостью, т.е. существуют такие числа а и b, при которых
.
(6.9)
6.
Утверждение 1 вытекает из очевидного соотношения
.
Если случайные величины и являются независимыми (и имеют математические ожидания), то
,
откуда приходим к утверждению 2.
Пусть
,
.
Тогда
Поэтому справедливо утверждение 3.
Рассмотрим дисперсию случайной величины
,
где х — произвольное число. В силу свойств дисперсий можно получить свойства 3 ковариации
.
Дисперсия
,
как
функции
от
x,
представляет
собой
квадратный трехчлен. Но дисперсия любой
случайной величины
не
может
быть меньше нуля, а это означает, что
дискриминант
(6.10)
квадратного трехчлена является неположительным, т.е. имеет место утверждение 4.
Далее, пусть выполнено равенство (6.8). Значит, дискриминант (6.10) равен нулю, и уравнение
=
0
имеет
решение, которое обозначим а. Тогда
случайная величина
принимает
всего одно значение (допустим, 6), и,
следовательно,
,
т.е. из (6.8) вытекает (6.9). Наоборот, пусть выполнено (6.9). Тогда в соответствии со свойством 1 дисперсии D(Ya) = 0, а значит, дискриминант (6.10) является неотрицательным. Поскольку при доказательстве утверждения 4 было показано, что этот дискриминант неположителен, то он равен нулю, откуда следует, что
.
Таким образом, из (6.9) вытекает (6.8). Утверждение 5 полностью доказано.
Наконец, раскрывая скобки в формуле, определяющей ковариацию, и используя свойства математического ожидания, получаем утверждение 6, которое часто бывает полезным при
численном подсчете ковариации.
Замечание . Если случайные величины связаны линейной зависимостью ,то в соответствии со свойствами 3 и 1
Поэтому знак ковариации совпадает со знаком коэффициента а и свойство 5 допускает следующее уточнение:
при
а
>
0;
при
a
< 0.
Определение 6.7. Случайные величины X и У называют некоррелированными, если их ковариация равна нулю, т.е.
cov(X,Y) = 0.
Приведенный выше пример показывает, что из некоррелированности случайных величин не следует их независимость, можно сказать, что ковариация случайных величин отражает, насколько их зависимость близка к линейной. Существенным недостатком ковариации является то, что ее размерность совпадает с произведением размерностей случайных величин. Естественно, хотелось бы иметь безразмерную
характеристику степени линейной зависимости. Но это очень просто сделать — достаточно поделить ковариацию случайных величин на произведение их средних квадратичных отклонений.
Определение
6.8. Коэффициентом
корреляции случайных
величин X
и
Y
называют
число
,
определяемое равенством (предполагается,
что D(X)
>
0 и D(Y)
> 0)
.
Теорема 6.5. Коэффициент корреляции имеет следующие свойства.
1.
= 1.
2.
Если случайные величины X
и
Y
являются
независимыми (и существуют D(X)
>0
и D(Y)
>0),
то
=
0.
3.
.
При
этом знак плюс нужно брать в том случае,
когда
и
имеют
одинаковое знаки, и минус — в противном
случае.
4.
.
5. | | = 1 тогда и только тогда, когда случайные величины X и Y связаны линейной зависимостью.
Доказательство теоремы следует из свойств ковариации, и мы предлагаем провести его самостоятельно.
Пример
6.6. Найдем
коэффициент корреляции случайных
величин X
—
числа очков, выпавших на верхней грани
игральной кости, и Y
—
на нижней (см. пример 5.5). Для этого сначала
вычислим M(X),
M(Y),
D(X),
D(Y)
и
.
Воспользовавшись табл. 5.3, получим
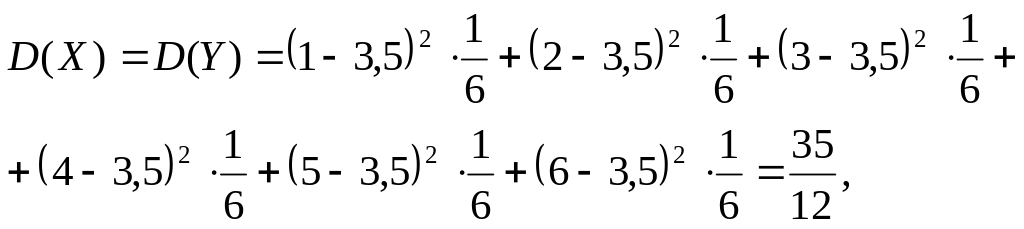
Аналогично можно вычислить:
Таким образом,
Впрочем,
это мы могли бы установить и без всяких
вычислений в силу свойства 5 коэффициента
корреляции, если бы вспомнили, что сумма
чисел очков на противоположных гранях
равна семи и, значит,
(X и Y связаны линейной зависимостью с отрицательным коэффициентом пропорциональности).