3.4. Формула полной вероятности

Предположим, что в результате опыта может произойти одно из п событий , которые удовлетворяют следующим двум условиям:

1) они являются попарно несовместными, т.е.

при i j;

2) хотя бы одно из них обязательно должно произойти в результате опыта, другими словами, их объединение есть достоверное событие, т.е.

.

Определение 3.5. События удовлетворяющие условиям 1 и 2, называют гипотезами.

Заметим, что если события удовлетворяют второму из двух указанных требований, то их совокупность называют полной группой событий. Таким образом, гипотезы — это попарно несовместные события, образующие полную группу событий.

Пусть также имеется некоторое событие А и известны вероятности гипотез , которые предполагаются ненулевыми, и условные вероятности события А при выполнении этих гипотез. Задача состоит в вычислении безусловной вероятности события А. Для решения этой задачи используют следующую теорему.

Теорема 3.6. Пусть для некоторого события А и гипотез известны , которые положительны, и

. (3.4)

Тогда безусловную вероятность Р(А) определяют по формуле

, (3.5)

которую называют формулой полной вероятности.

Представим событие А в виде

(на рис. 3.2, область, соответствующая событию А, заштрихована) .

С учетом того, что события несовместны, имеем

P(A) = .

В соответствии с формулой умножения вероятностей получаем

.

Поэтому

.

Формула полной вероятности при всей своей простоте играет весьма существенную роль в теории вероятностей.

Пример 3.7. Путник должен попасть из пункта В в пункт А в соответствии со схемой дорог изображенной на рис. 3.3. Выбор любой дороги в любом пункте равновозможен. Найдем вероятность события А — достижения путником намеченной цели.

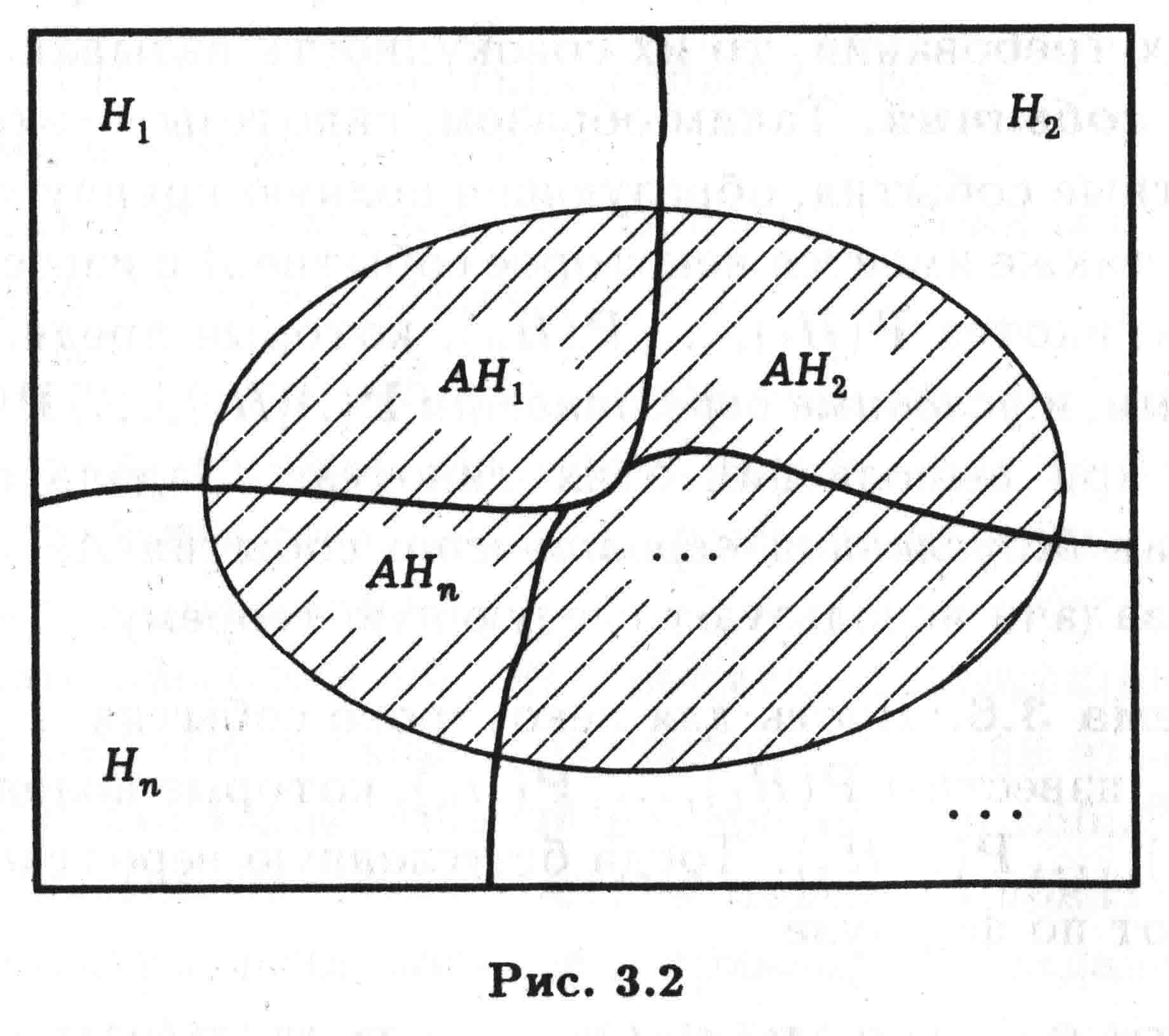
Рис.3.2

Для того чтобы попасть в пункт А, путник должен пройти один из промежуточных пунктов или . Введем гипотезы , где означает, что путник выбрал в пункте В путь, ведущий в пункт , i = 1,2,3. Ясно, что события несовместные и одно из них обязательно происходит, причем в силу равновозможности выбора дорог из B в

.

Остается вычислить условные вероятности , которые легко найти, если рассматривать новое пространство элементарных исходов, соответствующее выбранной гипотезе .

Например, появление означает, что есть два равновозможных исхода (из пункта выходят две дороги), из которых лишь один благоприятствует событию А, т.е. .

Аналогично находим, что

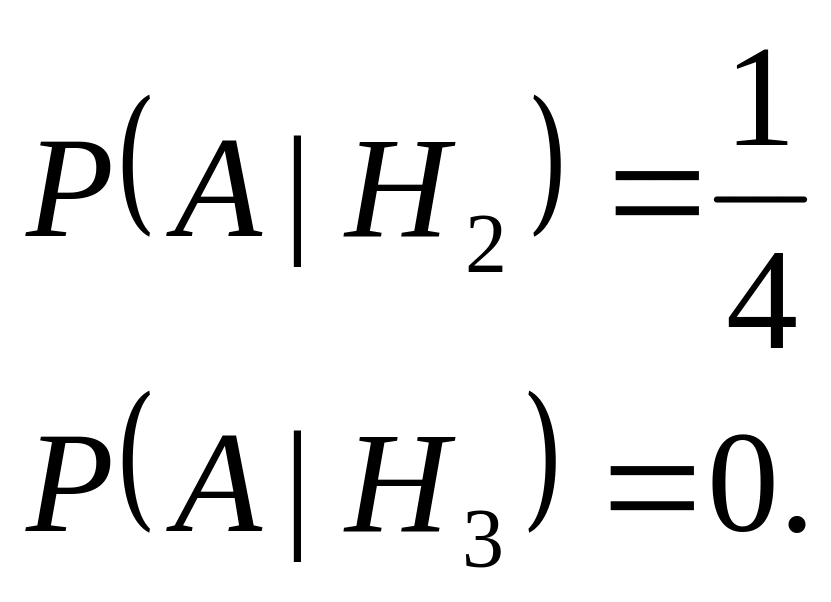
Согласно формуле 3.5 полной вероятности, получаем

.

Заметим, что данная задача может иметь техническую интерпретацию: сеть дорог — это сеть каналов передачи информации, а Р(А) — вероятность передачи сообщения по такой сети.

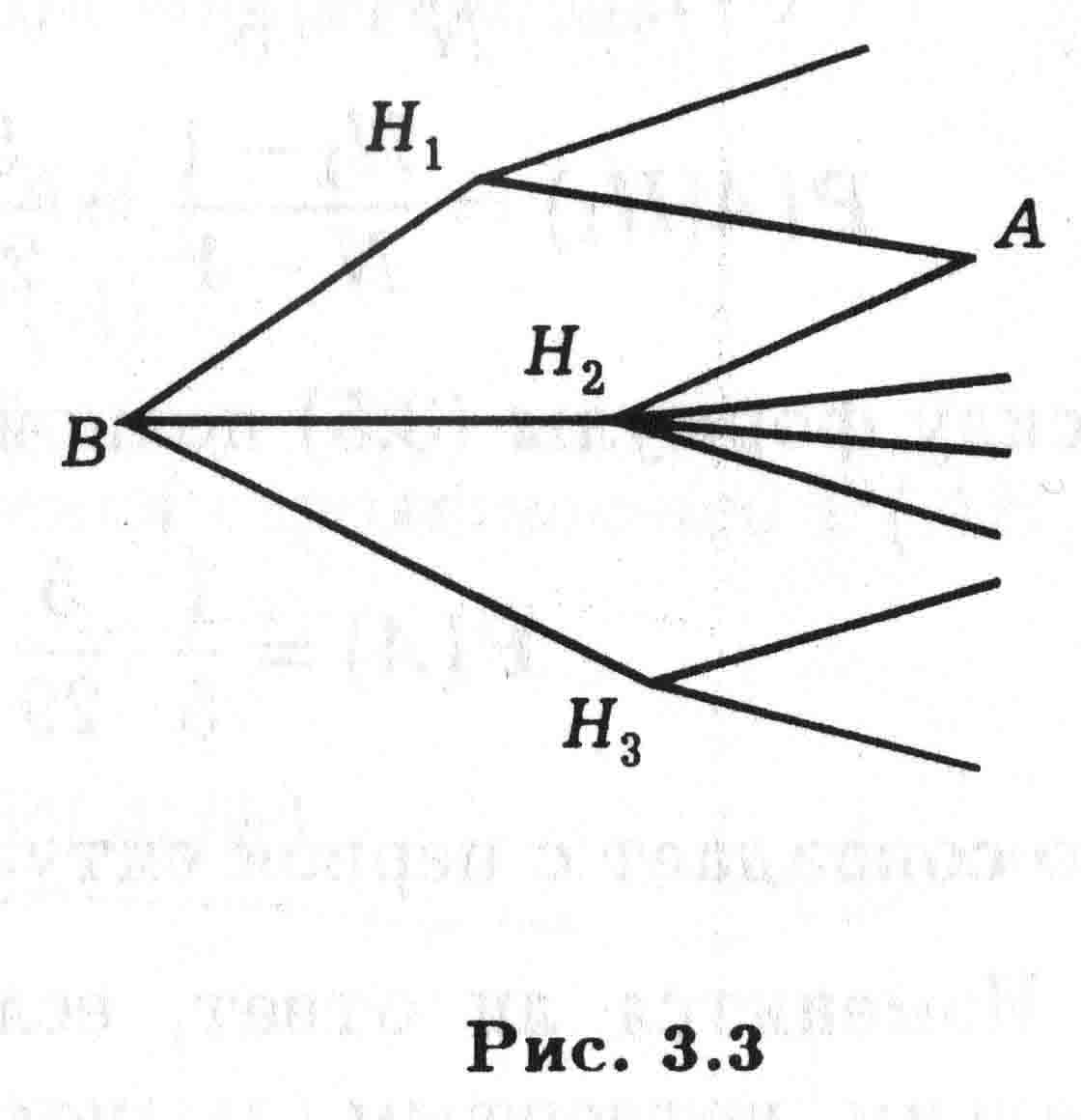
Рис. 3.3

Пример 3.8. Студент выучил все N = 30 экзаменационных билетов, но из них на „пять” — лишь = 6. Определим, зависит или нет вероятность извлечения „счастливого" билета (событие А) от того, первым или вторым выбирает студент свой билет.

Рассмотрим две ситуации.

Студент выбирает билет первым. Тогда

.

Студент выбирает билет вторым. Введем гипотезы: — первый извлеченный билет оказался „счастливым”, — „несчастливым”. Ясно, что

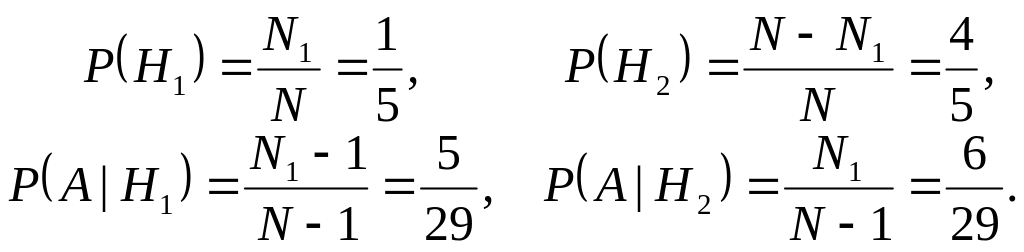
В силу формулы (3.5) полной вероятности

,

что совпадает с первой ситуацией.