3. Условная вероятность. Схема Бернулли

Рассмотрим события А и В, связанные с одним и тем же опытом. Пусть из каких-то источников нам стало известно, что событие В наступило, но не известно, какой конкретно из элементарных исходов, составляющих событие В, произошел. Что можно сказать в этом случае о вероятности события А?

Вероятность события А, вычисленную в предположении, что событие В произошло, принято называть условной вероятностью и обозначать Р(А|В).

Понятие условной вероятности играет важнейшую роль в современной теории вероятностей. Условная вероятность позволяет учитывать дополнительную информацию при определении вероятности события. В ряде случаев при помощи условной вероятности можно существенно упростить вычисление вероятности. Понятию условной вероятности и посвящена настоящая глава.

3.1. Определение условной вероятности

Предположим сначала, что мы находимся в рамках классической схемы. Пусть событиям А к В благоприятствуют и элементарных исходов соответственно. Посмотрим, что дает нам имеющаяся информация о событии В. Поскольку событие В произошло, то достоверно известно, что в результате опыта появился один из элементарных исходов, составляющих событие В. Значит, теперь уже при определении степени возможности события А необходимо выбирать только из возможных исходов, причем событию А благоприятствуют исходов, при которых происходят и событие А, и событие В, или, другими словами, происходит событие АВ. При этом по-прежнему будем считать все входящих в событие В исходов равновероятными. Поэтому условную вероятность Р(А|В) события А при условии события В в рамках классической схемы вероятности естественно определить как отношение числа исходов , благоприятствующих совместному осуществлению событий А и В, к числу исходов, благоприятствующих событию В, т.е.

.

Если теперь поделить числитель и знаменатель полученного выражения на общее число N элементарных исходов, то придем к формуле .

Обратимся теперь к статистическому определению вероятности.

Пусть п — общее число экспериментов; — число экспериментов, в которых наблюдалось событие А; — число экспериментов, в которых наблюдалось событие В, — число экспериментов, в которых наблюдалось событие АВ. Напомним, что частота события А — это отношение

.

Условной частотой события А при условии, что В произошло (будем обозначать ее ) естественно назвать частоту события А, но только не среди всех повторений опыта п, а лишь среди тех, в которых наблюдалось событие В, т.е.

Последнее выражение можно представить в виде

.

При п , согласно определению 2.6 статистической вероятности, , и, следовательно, условная частота

,

т.е. условной вероятностью события А при условии события В естественно назвать число = Р(АВ)/Р(В).

Таким образом, мы пришли к тому же самому выражению, что и в случае классической схемы.

На основании изложенного выше можно дать следующее определение.

Определение 3.1. Условной вероятностью события А при условии (наступлении) события В называют отношение вероятности пересечения событий А и В к вероятности события В:

. (3.1)

При этом предполагают, что Р(В) 0.

В связи с появлением термина „условная вероятность” будем вероятность события называть также безусловной вероятностью события.

Рассмотрим теперь условную вероятность Р(А|В) как функцию события А.

Теорема 3.1. Условная вероятность Р(А|В) обладает всеми свойствами безусловной вероятности Р(А).

Для доказательства достаточно показать, что условная вероятность Р(А|В) удовлетворяет аксиомам 1, 2 и 3.

Из определения 3.1 следует, что условная вероятность, удовлетворяет аксиоме неотрицательности, так как числитель дроби является неотрицательным числом, а знаменатель — положительным числом.

Поскольку B = В, то

,

т.е. условная вероятность удовлетворяет аксиоме нормированности.

Наконец, пусть — попарно непересекающиеся события. Тогда

и

,

где в последнем равенстве использовано свойство умножения сходящегося ряда на постоянную. Следовательно, условная вероятность удовлетворяет расширенной аксиоме сложения 3. Смысл теоремы 3.1 заключается в том, что условная вероят­ность представляет собой безусловную вероятность, заданную на новом пространстве элементарных исходов, совпадающем с событием В.

Пример 3.1. Рассмотрим опыт с однократным бросанием игральной кости, но не обычной, а с раскрашенными гранями: грани с цифрами 1, 3 и 6 окрашены красным, а грани с цифрами 2, 4 и 5 — белым цветом. Введем события: — впадение нечетного числа очков; — выпадение четного числа очков; В — появление грани красного цвета.

Интуитивно ясно, что если произошло событие В, то условная вероятность события больше, чем условная вероятность события А₂, поскольку на красных гранях нечетных чисел в два раза больше, чем четных. Заметим, что безусловные вероятности событий и А₂ при этом одинаковы и равны, очевидно, 1/2.

Найдем условные вероятности событий и А₂ при условии события В. Очевидно, что

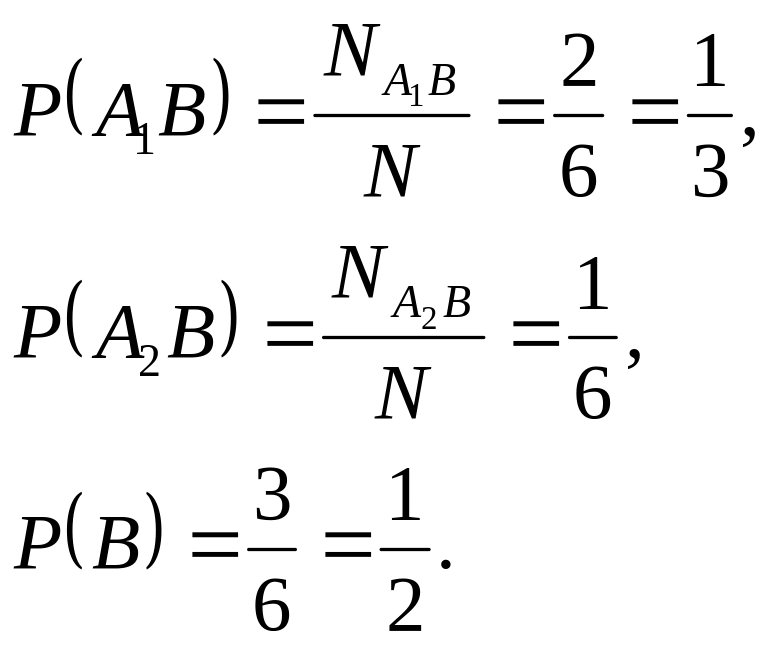
Следовательно, в силу определения 3.1 условной вероятности имеем и ,

что подтверждает наше предположение.

Геометрическая интерпретация условной вероятности. При практическом вычислении условной вероятности события А при условии, что событие В произошло, часто удобно трактовать условную вероятность как безусловную, но заданную не на исходном пространстве , элементарных исходов, а на новом пространстве = В элементарных исходов. Действительно, используя геометрическое определение вероятности, получаем для безусловной и условной вероятностей события А (на рис. 3.1 заштрихованная область соответствует событию АВ).

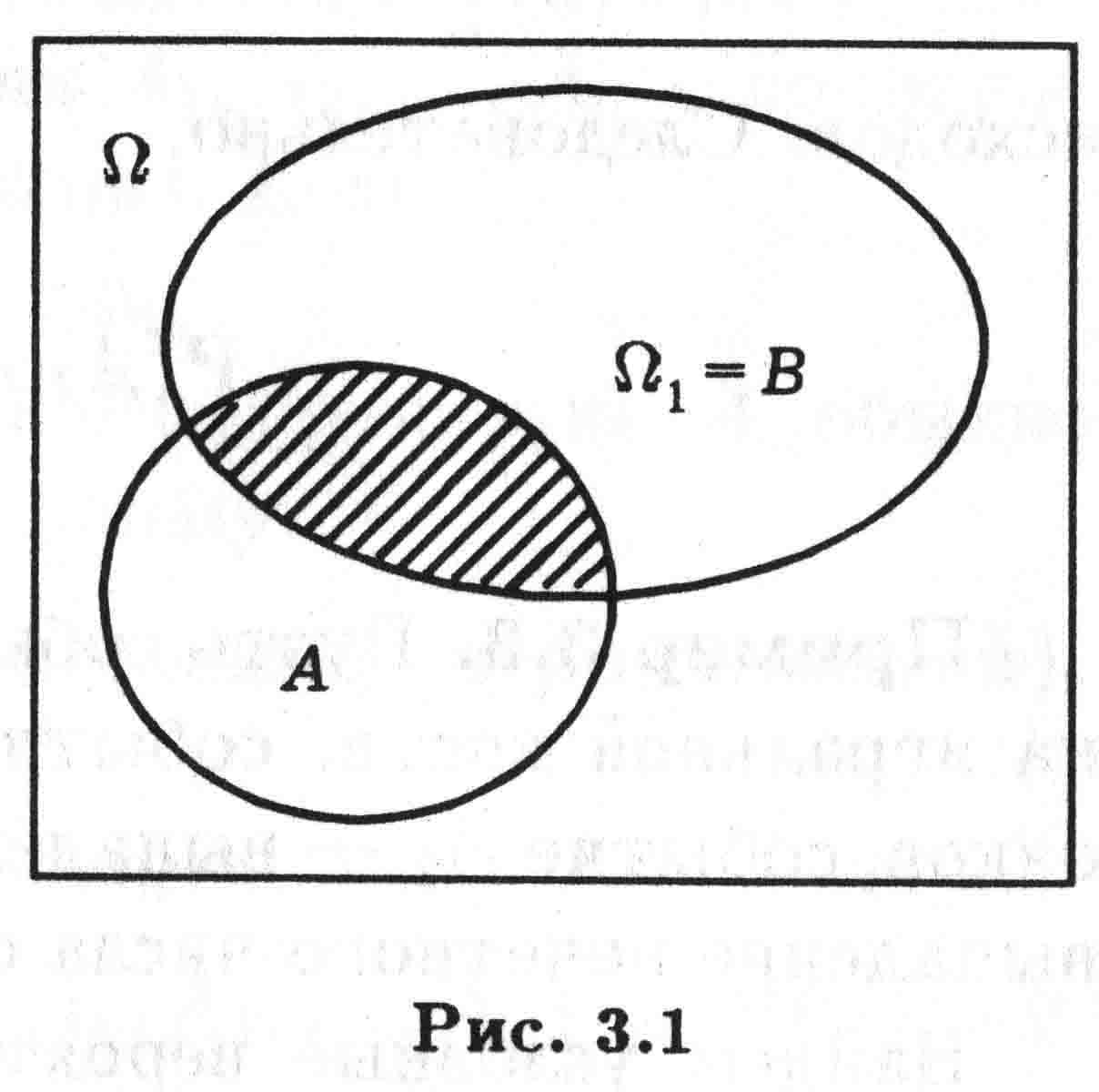
Рис. 3.1

Здесь и т.д. обозначают соответственно площади А, и т.д. Таким образом, выражение для Р(А|В) будет совпадать с выражением для Р(А), вычисленным в соответствии со схемой геометрической вероятности, если исходное пространство элементарных исходов заменить новым пространством = В.

Пример 3.2. Из урны, в которой а = 7 белых и b = 3 черных шаров, наугад без возвращения извлекают два шара. Пусть событие состоит в том, что первый извлеченный из урны шар является белым, а — белым является второй шар. Требуется найти P( ).

Приведем решение этой задачи двумя способами.

Первый способ. В соответствии с определением условной вероятности имеем (опуская пояснения):

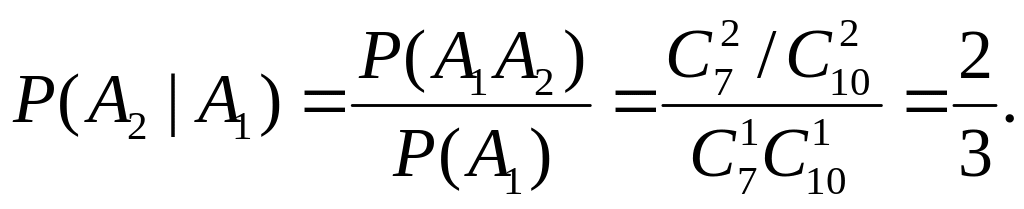
Второй способ. Перейдем к новому пространству элементарных исходов. Так как событие произошло, то это означает, что в новом пространстве элементарных исходов всего равновозможных исходов

а событию благоприятствует при этом

исходов. Следовательно,

.

Пример 3.3. Пусть событие В — выпадение 4 или 6 очков на игральной кости, событие — выпадение четного числа очков, событие — выпадение 3, 4 или 5 очков, событие — выпадение нечетного числа очков.

Найдем условные вероятности событий , и при условии события В.

Так как событие В принадлежит событию , то при наступлении события В событие обязательно произойдет, т.е. событие имеет условную вероятность

.

Поскольку события и В несовместные, то при наступлении события В событие уже не может произойти и его условная вероятность

.

Наконец, в соответствии с классической схемой вероятности приходим к следующему значению условной вероятности события при условии события В:

.

Заметим, что условная вероятность события при условии В совпадает с безусловной вероятностью события .