1.7. Масштабы планов и карт. Точность масштабов

Горизонтальные проложения отрезков местности при их изображении на планах и картах уменьшают.

Масштаб – это степень уменьшения горизонтальных проложений отрезков местности при их изображении на плане или карте.

Масштабы делятся на численные и графические.

Численный масштаб (рисунок 1.18 а) – это дробь, числитель которой равен единице, а знаменатель величине m, показывающей, во сколько раз уменьшены линии и предметы при изображении их на плане или карте.

На каждом листе карты или плана подписывается его численный масштаб в виде 1:1000, 1:2000, 1:5000, 1:10000, 1:25000 и т. д.

Если длину линии на плане (карте) обозначить через d, то ее горизонтальное проложение D на местности определяется по формуле

. (1.4)

Пример 1. На карте масштаба 1:5000 длина отрезка d = 25,4 мм. Определить длину горизонтального проложения D этого отрезка на местности.

По формуле (1.4) находим

D = 5000  25,4 мм = 127000 мм = 127 м.

Пример 2. Горизонтальное проложение отрезка на местности D = 284,7 м. Определить длину d этого отрезка на карте масштаба 1:25000.

Из формулы (1.4) получим

.

Следует заметить, что чем больше знаменатель m численного масштаба, тем масштаб мельче, и наоборот, чем меньше m, тем крупнее масштаб.

При решении задач по карте или плану с помощью численного масштаба приходится выполнять много вычислений. Чтобы избежать этого, используют графические масштабы. Графические масштабы бывают линейные и поперечные.

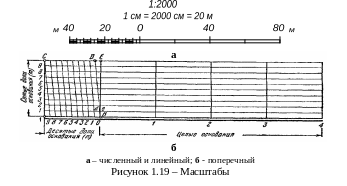
Линейный масштаб (рисунок 1.18 а) – это графическое выражение численного масштаба. Для построения линейного масштаба проводят прямую линию и на ней несколько раз откладывают одно и то же расстояние в сантиметрах, называемое основанием масштаба а. Основание обычно берут длиной в 1 или 2 сантиметра. Первое (левое) основание делят на 10 равных частей и на правом конце его пишут нуль, а на левом – то число метров или километров, которому на местности соответствует в данном масштабе основание. Вправо от нуля над каждым делением надписывают значения соответствующих расстояний на местности. Практическая точность линейного масштаба 0,5 мм, что соответствует 0,02-0,03 основания масштаба.

Пример 3. На карте масштаба 1:2000 необходимо с помощью измерителя отложить отрезок d, которому на местности соответствует горизонтальное проложение D = 97 м.

Конец одной (правой) иглы измерителя совмещается со штрихом 80 м, а конец второй (левой) иглы – с серединой между делениями 16 и 18 м левого основания линейного масштаба (рисунок 1.19 а). Расстояние между остриями игл измерителя будет равно отрезку d.

Пример 4. На карте масштаба 1:2000 длина отрезка d измерена измерителем. Определить с помощью измерителя длину горизонтального проложения D этого отрезка на местности. (Допустим d = 23,9 мм).

Измерителем фиксируют отрезок d на карте. Острие одной (правой) иглы совмещают со штрихом того основания, при котором острие второй (левой) иглы будет находиться в пределах левого основания линейного масштаба. Для d = 23,9 мм острие правой иглы совместится с основанием 40 м, а острие левой иглы поместится на левом крайнем основании между делениями 6 и 8 м. На глаз оценивают 7,8 м. Вся длина горизонтального проложения D будет равна 47,8 м.

Для более точных графических работ на плане пользуются поперечным масштабом, позволяющим измерять отрезки с точностью 0,01 его основания.

Поперечный масштаб (рисунок 1.18 б) представляет собой график, основанный на пропорциональном делении. Его создают путем прочерчивания на одинаковом расстоянии друг от друга 11 параллельных линий. Перпендикулярно этим линиям прочерчивают линии основания масштаба, обычно через 2 см. Крайний левый отрезок делят на 10 одинаковых частей, после чего соединяют нулевое нижнее деление с первым верхним, первое нижнее со вторым верхним и т. д. Таким образом, получают десятые и сотые доли левого основания.

Для определения наименьшего деления de (рисунок 1.18 б) из подобия треугольников ВDЕ и Вdе следует

или .

Учитывая, что и , будем иметь

, (1.5)

где n – число делений в основании масштаба;

m – число промежутков между параллельными линиями.

При n = m = 10, de = l и с учетом формулы (1.5) наименьшее деление поперечного масштаба равно сотой доле основания

. (1.6)

Невооруженный глаз может оценивать на карте расстояния до 0,1 мм. Поэтому горизонтальное расстояние на местности, соответствующее на карте 0,1 мм, называется точностью масштаба.

Для масштабов 1:500, 1:1000, 1:5000, 1:10000 и 1: 25000 точность масштаба соответственно равна 0,05; 0,1; 0,5; 1,0 и 2,5 м.

При решении самых разнообразных задач и, в частности, для проектирования границ земельных участков, водоемов, каналов, дорог, строений и т. д., требуется знать расположения объектов по отношению к сторонам света. Карты и планы составляют так, что их верхние края являются северными. В связи с этим при производстве измерений на земной поверхности необходимо линии ориентировать относительно какого-то исходного направления.