
- •А.И. Андреев и.В. Андреев
- •Воронеж 2015
- •1. Структура механизмов
- •2. Основные виды механизмов
- •3. Кинематический расчет механизмов
- •3.1. Аналитические методы исследования кинематики механизмов
- •4. Динамика механизмов
- •4.1. Силы, действующие на звенья
- •4.2. Определение крутящего момента на ведомом валу
- •4.3. Приведение масс в механизмах
- •4.4. Приведение сил и моментов сил в механизмах
- •5. Уравнения движения механизма
- •5.1. Уравнение движения механизма в интегральной форме, три стадии движения механизма
- •5.2. Механические характеристики электродвигателей
- •5.3. Уравнение движения механизма в дифференциальной
- •5.4. Трение в кинематических парах
- •5.5. Коэффициент полезного действия механизмов
- •6. Деформации и напряжения деталей
- •6.1. Деформация деталей, виды деформаций
- •6.2. Напряжения и метод сечений
- •7. Осевое растяжение и сжатие. Сдвиг
- •7.1. Напряжения и деформации при растяжении
- •7.2. Закон Гука и параметры кривой растяжения образца
- •7.3. Закон Гука для двухосного напряженного состояния
- •7.4. Определение твердости
- •Расчеты на прочность и жесткость
- •Деформации и напряжения при сдвиге
- •7.7. Закон Гука при сдвиге
- •8. Кручение и изгиб
- •8.1 Деформации и напряжения при кручении
- •8.2. Изгиб. Виды изгиба и их особенности. Типы опор и опорные реакции
- •8.3. Чистый изгиб балки
- •9. Характеристики плоских сечений и поперечный изгиб
- •9.1. Геометрические характеристики плоских сечений
- •Плоский поперечный изгиб. Изгибающий
- •Правила построения эпюр изгибающих моментов
- •Напряжения при поперечном изгибе. Расчеты
- •9.5. Прогиб балок. Расчеты на прочность
- •10. Прочность при сложных деформациях
- •10.1. Сложные деформации. Теории прочности
- •10.2. Пространственный изгиб
- •10.3. Совместное действие изгиба и растяжения (сжатия)
- •10.4. Совместное действие изгиба и кручения
- •11. Продольный изгиб. Прочность при переменных напряжениях
- •11.1. Устойчивость сжатых стержней. Формула Эйлера
- •11.2. Проверка сжатых стержней на устойчивость
- •11.3. Переменные напряжения. Выбор допускаемых напряжений
- •Концентрация напряжений и ее влияние
- •11.5. Определение допускаемых напряжений
- •12.4. Геометрические характеристики механизма
- •13. Силовой расчет механизмов
- •14. Расчет механизмов на прочность
- •14.1. Прочностные расчеты фрикционных передач
- •14.2. Износостойкость механизма винт–гайка
- •14.3. Расчет на прочность цилиндрических зубчатых передач
- •14.4. Расчет на прочность червячных передач
- •15. Определение прочности валов и осей механизмов
- •16. Основы конструирования механизмов и отдельных деталей передач
- •Проектирование червяков и червячных колёс
- •Конструирование деталей фрикционных передач
- •Конструкции валов и осей
- •Точность изготовления деталей
- •Размеры. Квалитеты. Система отверстия
- •Точность геометрической формы деталей
- •Заключение
- •Библиографический список
- •Оглавление
- •11. Продольный изгиб. Прочность при переменных
- •394026 Воронеж, Московский просп., 14
14.4. Расчет на прочность червячных передач
Расчет на контактную прочность зубьев червячного колеса проводят по аналогии с расчетом зубчатых передач по формуле (14.13), в которой величина нормальной нагрузки q на единицу длинны контактных линий колеса и червяка равна:
![]() .
(14.22)
.
(14.22)
В осевом сечении витки червяка имеют профиль прямообочной рейки с радиусом кривизны r1 = , поэтому приведенный радиус кривизны rпр червячной пары равен
кривизне профиля червячного колеса в полюсе зацепления и определяется выражением
![]() .
(14.23)
.
(14.23)
Приведенный модуль упругости Епр=2Е1Е2/ Е1+Е2, где Е1=2,1105 МПа – модуль упругости стального колеса и Е2=0,98105 МПа – модуль упругости бронзового колеса. В связи с этим приведенный модуль равен Епр=1,33105 МПа, принимая коэффициент Пуассона равным 12=0,3. Подставив выражения для q, rпр, Eпр в формулу (14.9) после преобразования получают формулу проверочного расчета на контактную прочность /1/
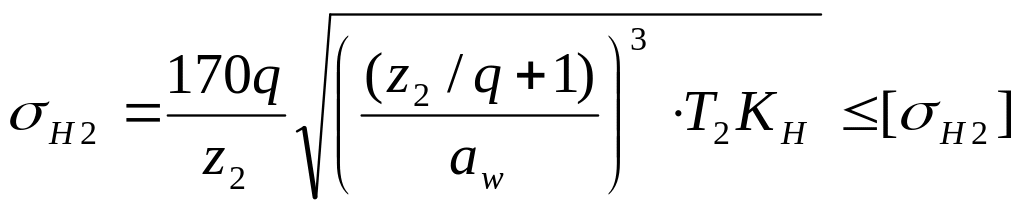 ,
(14.24)
,
(14.24)
где H2 и [H2] – расчетное и допускаемое контактные напряжения в зубьях колес, Н/мм2; aw – межосевое расстояние,
мм; T2 – вращающий момент на червячном колесе, Нмм.
Решив это уравнение относительно aw, получаем формулу проектировочного расчета червячных передач
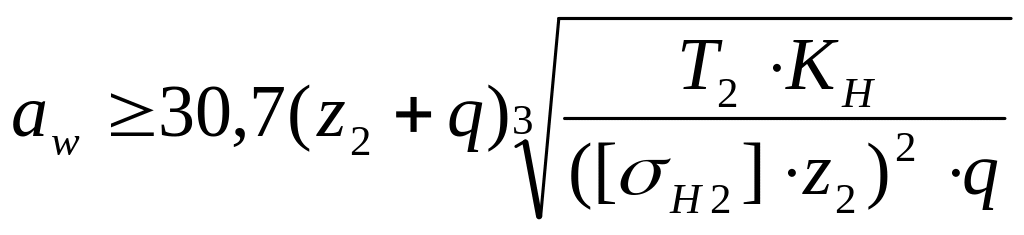 ,
(14.25)
,
(14.25)
где KH=KKV, величина К – коэффициент концентрации нагрузки, близкой к единице К1,0; КV – коэффициент динамической нагрузки, зависящий от окружной скорости червячного колеса V2. Окружную скорость V2 рассчитывают по формуле
![]() ,
(14.26)
,
(14.26)
где n1 – частота вращения червяка; U – передаточное число; d2 – делительный диаметр колеса.
Для окружной скорости червячного колеса V2 3 м/с принимают КV=1, а при V2>3 м/с принимают КV=1,11,3.
Далее определяют прочность зубьев червячного колеса на изгиб
![]() ,
(14.27)
,
(14.27)
где коэффициент формы зуба Yf2 выбирают в зависимости от эквивалентного числа зубьев колеса zv2=z2/cos3 (табл. 14.3).
Таблица 14.3
Значения параметра Yf2
Zv2 |
28 |
30 |
32 |
35 |
37 |
40 |
Yf2 2 |
1,8 |
1,76 |
1,71 |
1,64 |
1,61 |
1,56 |
Zv2 |
45 |
50 |
60 |
80 |
100 |
>100 |
Yf2
|
1,48 |
1,45 |
1,4 |
1,34 |
1,3 |
1,3 |
Коэффициент нагрузки равен Кf1,0. Допускаемые контактные напряжения для колес из оловянных бронз (Бр010Ф1 и др.) определяют из условия
![]() ,
(14.28)
,
(14.28)
где [H0] =0,9b – допускаемое контактное напряжение при числе циклов перемены напряжений NH=107; b – предел прочности бронзы при растяжении; Cv – коэффициент износа зубьев колеса зависит от скорости скольжения (табл. 14.4)
![]() (м
/с) (14.29)
(м
/с) (14.29)
KHl
– коэффициент долговечности равный
![]() ,
если N2>25107,
то KHl=0,67.
Обычно при полном ресурсе службы t=20000
ч. n1100
об/мин, KHl=0,76.
,
если N2>25107,
то KHl=0,67.
Обычно при полном ресурсе службы t=20000
ч. n1100
об/мин, KHl=0,76.
Таблица 14.4
Значения коэффициента Cv
VVs, м/с… |
1 1 |
22 |
33 |
44 |
55 |
66 |
77 |
8 |
CCv |
11.33 |
11.21 |
11.11 |
11.02 |
00.95 |
00.88 |
00.82 |
00.8 |
Допускаемые контактные напряжения для колес из оловянных бронз, латуней (БрА9ЖЗЛ, ЛЦ23А6Ж3Мц2) рассчитывают H2=300-25Vs (для бронз) и H2=375-25Vs (для латуней), они зависят от скорости скольжения Vs. Допускаемые напряжения изгиба при нереверсивной передаче (зубья работают одной стороной) для всех марок бронз и латуней
![]() ,
(14.30)
,
(14.30)
где
Т
– предел текучести; b
– предел прочности;![]() – коэффициент долговечности при расчете
на изгиб, Nz2
– число циклов нагружения зубьев колеса.
Если Nz2=106,
то Kfl=1,0;
при Nz2=9107,
Kfl=0,61.
– коэффициент долговечности при расчете
на изгиб, Nz2
– число циклов нагружения зубьев колеса.
Если Nz2=106,
то Kfl=1,0;
при Nz2=9107,
Kfl=0,61.
Обычно значение Кf1 выбирают равному последнему значению. При реверсивной передаче (зубья работают обеими сторонами) – [f]=0,8[f2].
Контрольные вопросы
От чего зависит величина контактной прочности
фрикционных передач с жесткими дисками?
Как определяются максимальные напряжения для
фрикционных передач с гибкой связью?
От чего зависят приведенный радиус и приведенный
модуль при расчете контактных напряжений?
Объясните методику расчета на контактную и
изгибную прочность цилиндрических прямозубых передач?
Как производится расчет на контактную и изгибную прочность конических зубчатых передач?
Чем отличается расчет контактных напряжений для червячных механизмов и для прямозубчатых передач?
Как производится расчет на контактную и изгибную прочность червячных зубчатых механизмов?
Каким образом определяются допускаемые контактные и изгибные напряжения для зубчатых стальных колес?
Как рассчитываются допускаемые контактные и
изгибные напряжения для червячной зубчатой передачи?
От чего зависит скорость скольжения червячного
колеса и как она влияет на величину контактных напряжений?
Каким образом определяются допускаемые контактные и изгибные напряжения для зубчатых колес, изготовленных из латуни, алюминиевых сплавов и пластмасс?
Как определяется коэффициент долговечности в зависимости от твердости стальных зубчатых колес?
Каким образом рассчитываются пределы контактной и изгибной выносливости и как влияет термообработка на
значение этих величин?
