
- •А.И. Андреев и.В. Андреев
- •Воронеж 2015
- •1. Структура механизмов
- •2. Основные виды механизмов
- •3. Кинематический расчет механизмов
- •3.1. Аналитические методы исследования кинематики механизмов
- •4. Динамика механизмов
- •4.1. Силы, действующие на звенья
- •4.2. Определение крутящего момента на ведомом валу
- •4.3. Приведение масс в механизмах
- •4.4. Приведение сил и моментов сил в механизмах
- •5. Уравнения движения механизма
- •5.1. Уравнение движения механизма в интегральной форме, три стадии движения механизма
- •5.2. Механические характеристики электродвигателей
- •5.3. Уравнение движения механизма в дифференциальной
- •5.4. Трение в кинематических парах
- •5.5. Коэффициент полезного действия механизмов
- •6. Деформации и напряжения деталей
- •6.1. Деформация деталей, виды деформаций
- •6.2. Напряжения и метод сечений
- •7. Осевое растяжение и сжатие. Сдвиг
- •7.1. Напряжения и деформации при растяжении
- •7.2. Закон Гука и параметры кривой растяжения образца
- •7.3. Закон Гука для двухосного напряженного состояния
- •7.4. Определение твердости
- •Расчеты на прочность и жесткость
- •Деформации и напряжения при сдвиге
- •7.7. Закон Гука при сдвиге
- •8. Кручение и изгиб
- •8.1 Деформации и напряжения при кручении
- •8.2. Изгиб. Виды изгиба и их особенности. Типы опор и опорные реакции
- •8.3. Чистый изгиб балки
- •9. Характеристики плоских сечений и поперечный изгиб
- •9.1. Геометрические характеристики плоских сечений
- •Плоский поперечный изгиб. Изгибающий
- •Правила построения эпюр изгибающих моментов
- •Напряжения при поперечном изгибе. Расчеты
- •9.5. Прогиб балок. Расчеты на прочность
- •10. Прочность при сложных деформациях
- •10.1. Сложные деформации. Теории прочности
- •10.2. Пространственный изгиб
- •10.3. Совместное действие изгиба и растяжения (сжатия)
- •10.4. Совместное действие изгиба и кручения
- •11. Продольный изгиб. Прочность при переменных напряжениях
- •11.1. Устойчивость сжатых стержней. Формула Эйлера
- •11.2. Проверка сжатых стержней на устойчивость
- •11.3. Переменные напряжения. Выбор допускаемых напряжений
- •Концентрация напряжений и ее влияние
- •11.5. Определение допускаемых напряжений
- •12.4. Геометрические характеристики механизма
- •13. Силовой расчет механизмов
- •14. Расчет механизмов на прочность
- •14.1. Прочностные расчеты фрикционных передач
- •14.2. Износостойкость механизма винт–гайка
- •14.3. Расчет на прочность цилиндрических зубчатых передач
- •14.4. Расчет на прочность червячных передач
- •15. Определение прочности валов и осей механизмов
- •16. Основы конструирования механизмов и отдельных деталей передач
- •Проектирование червяков и червячных колёс
- •Конструирование деталей фрикционных передач
- •Конструкции валов и осей
- •Точность изготовления деталей
- •Размеры. Квалитеты. Система отверстия
- •Точность геометрической формы деталей
- •Заключение
- •Библиографический список
- •Оглавление
- •11. Продольный изгиб. Прочность при переменных
- •394026 Воронеж, Московский просп., 14
Плоский поперечный изгиб. Изгибающий
момент и поперечная сила
Детали механизмов РЭС часто подвергаются
плоскому поперечному изгибу. Он отличается
от чистого изгиба тем, что в сечениях
балки одновременно действуют как
изгибающий момент, так и поперечная
сила. Однако зависимости (8.18) и (8.20),
полученные при рассмотрении чистого
изгиба справедливы и для плоского
поперечного изгиба. Прежде чем перейти
к расчету на прочность, определим
изгибающие моменты и поперечные силы
в сечениях балки. Изгибающий момент
![]() и поперечная сила Q
выступают статическим эквивалентом
внутренних сил взаимодействия напряжений,
возникающих в поперечном сечении балки.
Причем
связаны с нормальными напряжениями
,
а Q – с касательными
напряжениями
.
Пусть на балку действуют внешние силы
F1 и F2.(рис.
9.3). Опорные реакции RA
и RВ могут
быть найдены на основе уравнений статики.
Для рассмотрения применим метод сечений.
Мысленно расчленим балку плоскостью
m-m1.
Влияние одной части на другую заменим
поперечной силой Q и
моментом
,
которые эквивалентны всем внутренним
силам взаимодействия. Так как вся балка
находится в равновесии, то сила Q
и момент
должны иметь такие значения, при которых
в равновесии остается и каждая из двух
частей балки. При этом можно рассматривать
равновесие любой из частей балки.
Определение силы Q и
момента
рассмотрим, например, для левой отсеченной
части балки
и поперечная сила Q
выступают статическим эквивалентом
внутренних сил взаимодействия напряжений,
возникающих в поперечном сечении балки.
Причем
связаны с нормальными напряжениями
,
а Q – с касательными
напряжениями
.
Пусть на балку действуют внешние силы
F1 и F2.(рис.
9.3). Опорные реакции RA
и RВ могут
быть найдены на основе уравнений статики.
Для рассмотрения применим метод сечений.
Мысленно расчленим балку плоскостью
m-m1.
Влияние одной части на другую заменим
поперечной силой Q и
моментом
,
которые эквивалентны всем внутренним
силам взаимодействия. Так как вся балка
находится в равновесии, то сила Q
и момент
должны иметь такие значения, при которых
в равновесии остается и каждая из двух
частей балки. При этом можно рассматривать
равновесие любой из частей балки.
Определение силы Q и
момента
рассмотрим, например, для левой отсеченной
части балки
![]() ;
;
![]() ;
;
![]() (9.16)
(9.16)
![]() ;
;
![]() ,
,
![]() ,
(9.17)
,
(9.17)
При поперечном изгибе балки в результате действия внешних нагрузок в перечном сечении возникают внутренние усилия - изгибающий момент и поперечная сила Q. Изгибающий момент в любом сечении балки равен алгебраической сумме моментов всех внешних нагрузок, приложенных по одну сторону сечения и взятых относительно оси, проходящей через центр тяжести и перпендикулярно плоскости изгиба
![]() , (9.18)
, (9.18)
где
![]() ,
,
![]() ,
,
![]() -нагрузки
(включая распределенные) и внутренние
моменты
,
действующие на рассмотренную часть
балки, xi
и xj
–расстояния от линии действия сил до
плоского сечения.
-нагрузки
(включая распределенные) и внутренние
моменты
,
действующие на рассмотренную часть
балки, xi
и xj
–расстояния от линии действия сил до
плоского сечения.
Знак изгибающего момента принимается
положительным, если изогнутая балка
обращена выпуклостью вниз и отрицательным,
если выпуклость балки направлена вверх.
Поперечная сила
![]() равна
алгебраической сумме проекций на ось,
перпендикулярную оси балки, всех сил,
приложенных к рассмотренной части балки
равна
алгебраической сумме проекций на ось,
перпендикулярную оси балки, всех сил,
приложенных к рассмотренной части балки
![]() .
(9.19)
.
(9.19)
Знак поперечной силы принимается положительным, если сила действующая на балку слева направлена вверх, а сила действующая на балку справа вниз.
Знак поперечной силы принимается отрицательным, если сила действующая на балку слева направлена вниз, а сила действующая на балку справа вверх.
В теории изгиба устанавливается дифференциальная связь между изгибающим моментом и поперечной силой, между поперечной силой и распределенной нагрузкой.
Пусть на балку действует распределенная нагрузка интенсивностью q (рис. 9.4 а). Выделим из балки бесконечно малый элемент длиной dx (рис. 9.4 б) и составим уравнение равновесия
![]() ,
,
![]()
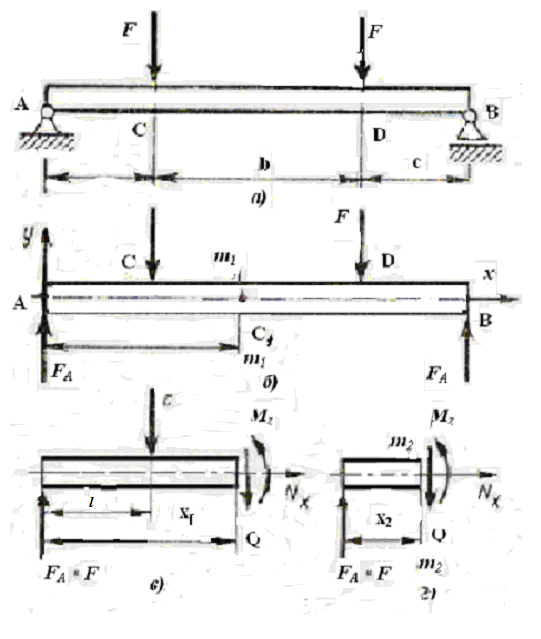
Рис. 9.3 Изгибающий момент и поперечная сила
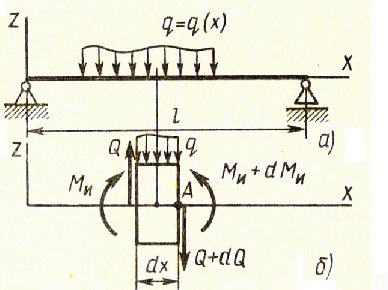
Рис. 9.4. Связь между изгибающим моментом и поперечной силой
Последнее слагаемое имеет величину второго порядка малости и его можно не учитывать, тогда получаем
![]() ,
(9.20)
,
(9.20)
Второе уравнение равновесия сил, действующих на элемент, имеет вид
,
![]() ,
,
откуда
![]() .
(9.21)
.
(9.21)
Таким образом, поперечная сила в каком- либо сечении балки равна производной от изгибающего момента. Если балка имеет распределенную нагрузку интенсивностью q, то производная от поперечной силы равна –q.
