9. Характеристики плоских сечений и поперечный изгиб

9.1. Геометрические характеристики плоских сечений

В теории изгиба и кручения используются следующие характеристики поперечных сечений деформируемых тел:

осевые моменты инерции плоских фигур, представляющие собой интегральную сумму произведений элементарных площадей dA на квадрат расстояния их до соответствующих осей

, , (9.1)

полярный момент инерции плоского сечения, равный

, (9.2)

а - расстояние площадки до начала координат и учитывая, что имеем

, (9.3)

центробежный момент инерции сечения , представляющий интеграл вида

, (9.4)

осевые и полярные моменты сопротивления сечений

, , , (9.5)

где , , - наибольшие расстояния точек сечений до осей Y, Z и начала координат. Оси Y и Z плоской фигуры можно расположить так, что центробежный момент инерции относительно этих осей равен нулю. Такие оси координат называются главными осями инерции сечения. Моменты инерции сечения и относительно главных осей имеют экстремальные значения, один из них максимален , а другой минимален . Часто начало главных осей инерции совпадает с центром тяжести. Такие оси называют главными центральными осями инерции сечения. Если плоская фигура имеет оси симметрии, то главные центральные оси инерции совпадают с ними. Рассмотрим моменты инерции для прямоугольного сечения (рис. 9.1 а).

Пусть в прямоугольном сечении высотой h и шириной b оси Y и Z – главные центральные оси инерции. Выделим элемент площади сечения на расстоянии z от оси y и найдем момент инерции сечения относительно оси y на основании формулы

. (9.6)

Аналогично можно найти

. (9.7)

Единица измерения момента инерции в системе СИ- . Моменты сопротивлений прямоугольного сечения балки вычисляют по формулам

, (9.8)

. (9.9)

При этом моменты инерции прямоугольного сечения, вычисленные относительно оснований, будут равны

, . (9.10)

Определим моменты инерции для круглого сечения (рис. 9.1 б). Выделим в сечении круга радиуса r элементарное кольцо радиусом , шириной и площадью . Полярный момент инерции этого сечения может быть определен по формуле

. (9.11)

Осевые моменты инерции круглого сечения равны между собой, поэтому получим

. (9.12)

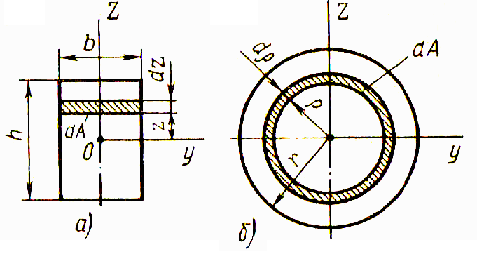
Рис. 9.1. Прямоугольное и круглое сечения балки

Осевые моменты сопротивлений будут равны

. (9.13)

Часто выражают через диаметр сечения

.

Полярный момент сопротивления сечения, используемый в расчетах при деформации кручения равен

.

Для сложного сечения, которое часто можно рассматривать составленное из нескольких простых сечений, при определении используют зависимости между моментами инерции относительно параллельных осей. Рассмотрим двутавровую балку (рис. 9.2 б), у которой относительно главных центральных осей y и z известны моменты инерции J_y и J_z и сечение имеет площадь A. Требуется определить моменты инерции этой фигуры относительно новых осей y₁ и z₁, которые параллельны главным центральным и расположены на расстояниях a и b от них ( рис. 9.2 а).

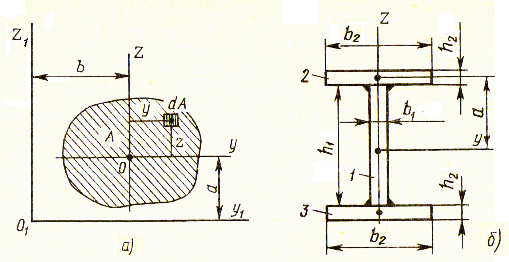
Рис. 9.2. Определение момента инерции сложного сечения

Используя формулы (9.1) имеем

Второй интеграл представляет статический момент сечения относительно оси y, проходящей через его центр тяжести и равен нулю, т.е.

.

Тогда получаем

. (9.14)

Аналогично находим

. (9.15)

Эти выражения получили название теоремы Штейнера.